0-1背包问题（动态规划）C语言实现

算法设计中经典的0-1背包问题

这里背包问题的贪心算法的思路就用不了了

问题如下：

        给定n种物品和一背包。物品i的重量是wi，其价值为vi，背包的容量为C。问:应如何选择装入背包的物品，使得装入背包中物品的总价值最大?在选择装入背包的物品时，对每种物品i只有两种选择，即装入背包或者不装入背包。不能将物品i装入背包多次，也不能只装入部分物品i。设计一个动态规划的算法解决此问题。

        形式化描述：给定c >0, wi >0, vi >0 , 1≤i≤n.要求找一n元向量(x1,x2,…,xn,), xi∈{0,1}, ∋ ∑ wi xi≤c,且∑ vi xi达最大.即一个特殊的整数规划问题。

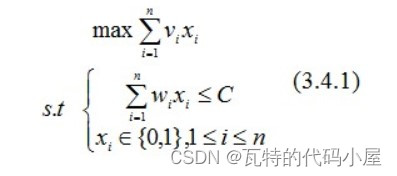
         递推关系：

        设所给0-1背包问题子问题的最优值为m(i，j)，即m(i，j)是背包容量为j，可选择物品为i，i+1，…，n时0-1背包问题的最优值。由0-1背包问题的最优子结构性质，可以建立计算m(i，j)的递归式:

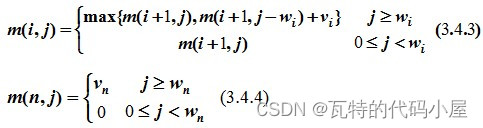
           上式此时背包容量为j，可选择物品为i。此时在对xi作出决策之后,问题可能处于两种状态:
                    (1)、背包剩余容量是j,没产生任何效益；
                    (2)、剩余容量j-wi,效益值增长了vi ；

关于这道题，其实就是利用动态规划的一种思想，解这道题有点类似冒泡，采用遍历数组序列，不断更新递增序列的长度以至于来找到最长单调递增序列。

代码实现如下：（C语言实现）

#include<stdio.h>
const int N = 4;

void Knapsack(int v[],int w[],int c,int n,int m[][10]);
void Traceback(int m[][10],int w[],int c,int n,int x[]);
int getMin(int a,int b);
int getMax(int a,int b);

int main()
{
    int c=8;
    int v[]= {0,2,1,4,3},w[]= {0,1,4,2,3}; //下标从1开始
    int x[N+1];
    int m[10][10];

    printf("待装物品重量分别为：\n");
    for(int i=1; i<=N; i++)
    {
        printf("%d ",w[i]);
    }
    puts("");

    printf("待装物品价值分别为：\n");
    for(int i=1; i<=N; i++)
    {
        printf("%d ",v[i]);
    }
    puts("");

    Knapsack(v,w,c,N,m);

    printf("背包能装的最大价值为：%d\n",m[1][c]);

    Traceback(m,w,c,N,x);
    printf("背包装下的物品编号为：\n");
    for(int i=1; i<=N; i++)
    {
        if(x[i]==1)
        {
            printf("%d ",i);
        }
    }
    puts("");

    return 0;
}

void Knapsack(int v[],int w[],int c,int n,int m[][10])
{
    int jMax = getMin(w[n]-1,c);//背包剩余容量上限 范围[0~w[n]-1]
    for(int j=0; j<=jMax; j++)
    {
        m[n][j]=0;
    }

    for(int j=w[n]; j<=c; j++)//限制范围[w[n]~c]
    {
        m[n][j] = v[n];
    }

    for(int i=n-1; i>1; i--)
    {
        jMax = getMin(w[i]-1,c);
        for(int j=0; j<=jMax; j++)//背包不同剩余容量j<=jMax<c
        {
            m[i][j] = m[i+1][j];//没产生任何效益
        }

        for(int j=w[i]; j<=c; j++) //背包不同剩余容量j-wi >c
        {
            m[i][j] = getMax(m[i+1][j],m[i+1][j-w[i]]+v[i]);//效益值增长vi
        }
    }
    m[1][c] = m[2][c];
    if(c>=w[1])
    {
        m[1][c] = getMax(m[1][c],m[2][c-w[1]]+v[1]);
    }
}

//x[]数组存储对应物品0-1向量,0不装入背包，1表示装入背包
void Traceback(int m[][10],int w[],int c,int n,int x[])
{
    for(int i=1; i<n; i++)
    {
        if(m[i][c] == m[i+1][c])
        {
            x[i]=0;
        }
        else
        {
            x[i]=1;
            c-=w[i];
        }
    }
    x[n]=(m[n][c])?1:0;
}
int getMin(int a,int b)
{
    if(a>=b)
        return b;
    else
        return a;
}
int getMax(int a, int b)
{
    if(a>=b)
        return a;
    else
        return b;
}

算法复杂性分析

算法的复杂性：O(nc)计算时间。当背包容量c很大时，算法需要的计算时间较多。例如，当c>2^n时，算法需要Ω(n2^n)计算时间。

还有阶跃性优化具体参照《算法设计与分析第五版》

链接: https://pan.baidu.com/s/1wzfrTUvP1GrVwaXElgbl5w

提取码: 3mk9