【现代密码学】笔记3.4-3.7--构造安全加密方案、CPA安全、CCA安全《introduction to modern cryphtography》

教IT的小强

于 2024-03-25 11:00:00 发布

阅读量2k

点赞数 22

文章标签：密码学笔记安全

本文链接：https://blog.csdn.net/m0_59598029/article/details/136950922

版权

【现代密码学】笔记3.4-3.7–构造安全加密方案、CPA安全、CCA安全《introduction to modern

cryphtography》

写在最前面
私钥加密与伪随机性第二部分

* 流加密与CPA

```
      * 多重加密
```
CPA安全加密方案

      * CPA安全实验、预言机访问（oracle access）

操作模式
```
      * 伪随机函数PRF
```
- 伪随机排列PRP
CCA安全加密方案
```
      * 补充
```
- 填充预言机Padding-Oracle攻击真实案例

写在最前面

主要在哈工大密码学课程张宇老师课件的基础上学习记录笔记。

内容补充：骆婷老师的PPT
《introduction to modern cryphtography》–Jonathan Katz, Yehuda
Lindell（现代密码学——原理与协议）中相关章节
密码学复习笔记这个博主好有意思

初步笔记，如有错误请指正

快速补充一些密码相关的背景知识

![请添加图片描述](https://img-
blog.csdnimg.cn/direct/8d888f7ea08e469cac997cce7c00e801.png)

私钥加密与伪随机性第二部分

本节课学习另外两种私钥加密安全理论：选择明文攻击（CPA）下不可区分性、选择密文攻击（CCA）下不可区分性以及相关的密码学原语、假设、构造和证明。这些攻击更好的刻画了现实世界中敌手的能力，相应的密码学方案也是目前真正在实际使用的。
目录：流加密与CPA，CPA安全加密方案，操作模式，CCA安全加密方案

流加密与CPA

流加密方案（Stream Cipher）

* 首先介绍当有多个消息需要被传递时，如何利用之前学习的基于PRG的加密方案来保护消息。
* 思路：受一次一密方案的启发，通过将变长消息与密钥的异或来加密
* 流加密方案：通过将多个消息“拼成”一个消息，与伪随机的比特流（密钥流）异或来加密
* 密钥流：由一个变长的伪随机生成器产生
* 优点：逻辑简单，比分组密码更快
* 缺点：难以做到安全

采用流加密方案的安全多重加密

* 同步模式：用一个流中不同部分分别加密各个消息；
* 异步模式：以密钥和初始向量一起作为输入来产生流，每个明文的加密采用相同的密钥和不同的初始向量 
  * **初始向量（Initial Vector）** ， I V IV IV是随机选取的并且是公开的；其生成是随机的并不受控制，但生成后并不保密；密钥的生成是随机的并不受控制，但生成后也要保密。
* 两种模式差异： 
  * 同步模式适合持续通信场景，例如语音；异步模式适合间断通信场景，例如即时消息。

流密码的安全性

1. 现状：没有标准化和流行的方案，安全性仍有疑问，例如在802.11中WEP协议的RC4，线性反馈移位寄存器（Linear Feedback Shift Registers）；
2. 警告：不要使用任何流加密方案，如果一定需要的话，采用由分组加密方案构造的。
3. eStream项目致力于设计安全的流密码

相关密钥：真实世界例子

* 用于多重加密的密钥（初始向量和密钥对）必须是独立的。否则，前面的攻击就会生效；
* 对于802.11b WEP的若干攻击： 
  * WEP为异步模式， E n c ( m i ) : = < I V i , G ( I V i ∥ k ) ⊕ m i > \mathsf{Enc}(m_i) := \left< IV_i, G(IV_i\|k) \oplus m_i\right> Enc(mi):=⟨IVi,G(IVi∥k)⊕mi⟩
  * I V IV IV长度为24比特，在 2 24 ≈ 2^{24} \approx 224≈ 16M 帧后 I V IV IV会产生重复；
  * 在一些WiFi网卡上，在电源重启后 I V IV IV重置为0；
  * I V i = I V i − 1 \+ 1 IV_i = IV_{i-1} + 1 IVi=IVi−1+1. 对于RC4，在40,000帧后可以恢复  k k k ；

多重加密

多重加密（Multiple Encryptions）

* 在一次一密中，一个密钥不可以用于对多个消息的加密；否则，就是不安全的。如果敌手能够获得用同一个密钥加密后的多个密文，则之前的方案都是不安全的；为此，我们需要新的加密方案来防御这样的攻击。
* 多个明文的加密实验 P r i v K A , Π m u l t ( n ) \mathsf{PrivK}^{\mathsf{mult}}_{\mathcal{A},\Pi}(n) PrivKA,Πmult(n)，当一次加密多个明文时，窃听者敌手能够区分出两组明文吗？
* 一个敌手 A \mathcal{A} A与一个挑战者 C \mathcal{C} C进行3轮交互： 
  1. A \mathcal{A} A选择两个长度相同、内容不同明文向量 M ⃗ 0 = ( m 0 1 , … , m 0 t ) \vec{M}_0=(m_0^1,\dots,m_0^t) M 0=(m01,…,m0t),  M ⃗ 1 = ( m 1 1 , … , m 1 t ) \vec{M}_1=(m_1^1,\dots,m_1^t) M 1=(m11,…,m1t)，其中两个向量中同一位置的明文长度相同 ∀ i , ∣ m 0 i ∣ = ∣ m 1 i ∣ \forall i, |m_0^i| = |m_1^i| ∀i,∣m0i∣=∣m1i∣，发送给 C \mathcal{C} C；
  2. C \mathcal{C} C根据密钥生成算法生成一个新密钥 k ← G e n ( 1 n ) k \gets \mathsf{Gen}(1^n) k←Gen(1n)，一个随机比特 b ← { 0 , 1 } b \gets \\{0,1\\} b←{0,1}。对向量 M ⃗ b \vec{M}_b M b中每个明文加密  c i ← E n c k ( m b i ) c^i \gets \mathsf{Enc}_k(m_b^i) ci←Enck(mbi) 得到一个密文向量  C ⃗ = ( c 1 , … , c t ) \vec{C}=(c^1,\dots,c^t) C =(c1,…,ct) ，并发送给 A \mathcal{A} A；
  3. A \mathcal{A} A输出对所加密明文向量的猜测 b ′ b' b′，若 b = b ′ b=b' b=b′，则 A \mathcal{A} A成功；否则，失败；
* 这与之前的单个消息不可区分实验类似的，区别在于 **用同一个密钥加密的多个消息** 。敌手可以获得多个明文的密文，比单个明文不可区分实验中的敌手有更强的能力。

多重加密安全定义

* Π \Pi Π 是 **窃听者出现时不可区分的多重加密方案** ，如果任意PPT的敌手 A \mathcal{A} A, 存在可忽略的函数 n e g l \mathsf{negl} negl 使得

Pr ⁡ [ P r i v K A , Π m u l t ( n ) = 1 ] ≤ 1 2 + n e g l ( n ) .
\Pr\left[\mathsf{PrivK}^{\mathsf{mult}}_{\mathcal{A},\Pi}(n)=1\right] \le
\frac{1}{2} + \mathsf{negl}(n). Pr[PrivKA,Πmult(n)=1]≤21+negl(n).

* 根据这个定义，来分析迄今学习的密码学方案是否是多重加密不可区分的？

攻击确定性加密方案

* 问题：如果一个加密方案中加密算法是确定性的，即同一个明文会被同一个密钥加密成同一个密文，那么该加密方案是`多重加密安全`的吗？
* 攻击：对于确定性加密方案，敌手可以构造 m 0 1 = m 0 2 m_0^1 = m_0^2 m01=m02 并且  m 1 1 ≠ m 1 2 m_1^1 \neq m_1^2 m11=m12，然后当 c 1 = c 2 c^1 = c^2 c1=c2，输出  b ′ = 0 b'=0 b′=0，否则  b ′ = 1 b'=1 b′=1。
* 因此，确定性加密方案不是多重加密安全的，我们需要新的密码学原语来防御多重加密攻击。接下来，我们介绍一种更强的攻击，其涵盖了多重加密攻击。只要防御了这个新定义的攻击，也就同时防御了多重加密攻击。

CPA安全加密方案

选择明文攻击（ Chosen-Plaintext Attacks (CPA) ）（思考）

* 敌手具有获得其所选择明文对应的密文的能力。

* 第二次世界大战中的例子：美国海军密码分析学家相信密文“AF”表示日语中的“中途岛”；但美国将军不认为中途岛会遭到攻击（？这里没看懂）；美国海军密码分析学家发送了一个明文，中途岛淡水供给不足；日本军队截获的明文，并发送了一段密文，“AF”淡水不足；美国军队派出三艘航空母舰并且取胜。

* 这里例子里，美国海军密码分析学家选择了明文并得到了密文。

CPA安全实验、预言机访问（oracle access）

CPA安全实验

* CPA不可区分实验  P r i v K A , Π c p a ( n ) \mathsf{PrivK}^{\mathsf{cpa}}_{\mathcal{A},\Pi}(n) PrivKA,Πcpa(n): 
  1. 挑战者生成密钥  k ← G e n ( 1 n ) k \gets \mathsf{Gen}(1^n) k←Gen(1n)；（这里与窃听者不可区分实验相比，密钥的生成提前了，这是为了下一步提供加密预言机）
  2. A \mathcal{A} A 被给予输入  1 n 1^n 1n 和对加密函数  E n c k ( ⋅ ) \mathsf{Enc}_k(\cdot) Enck(⋅)的 **预言机访问（oracle access）** A E n c k ( ⋅ ) \mathcal{A}^{\mathsf{Enc}_k(\cdot)} AEnck(⋅) ，输出相同长度  m 0 , m 1 m_0, m_1 m0,m1 ；
  3. 挑战者生成随机比特  b ← { 0 , 1 } b \gets \\{0,1\\} b←{0,1}，将挑战密文  c ← E n c k ( m b ) c \gets \mathsf{Enc}_k(m_b) c←Enck(mb) 发送给  A \mathcal{A} A；
  4. A \mathcal{A} A 继续对  E n c k ( ⋅ ) \mathsf{Enc}_k(\cdot) Enck(⋅)的预言机的访问，输出 b ′ b' b′；如果 b ′ = b b' = b b′=b，则 A \mathcal{A} A成功 P r i v K A , Π c p a = 1 \mathsf{PrivK}^{\mathsf{cpa}}_{\mathcal{A},\Pi}=1 PrivKA,Πcpa=1，否则 0。
* 敌手对加密函数预言机访问是指，敌手以任意明文作为输入，可以从预言机得到对应密文。此处，密钥是已经提前生成的，因此才能通过加密函数预研机得到密文，但仍对敌手保密。`预言机`是一个形象的比喻，它是一个黑盒，只接收输入并返回输出；访问者不需要了解其内部构造。
* 该实验与窃听者不可区分实验的区别在于，敌手可访问加密预言机，在实验过程中始终可以，包括在产生两个明文阶段，以及在收到挑战密文后猜测被加密明文阶段，获得任意明文被同一密钥加密的密文；而且密文是逐个获得，可以根据之前的明文和密文对来“适应性地”构造新的查询。
* CPA敌手比多重加密的敌手更“强大”，因为多重加密敌手是可以一次性地获得一组密文，而CPA敌手可以根据已经获得的明文和密文“多次适应性地”再次获得密文。

CPA安全

* Π \Pi Π 是CPA不可区分加密方案 (CPA安全的)，如果任意概率多项式时间算法 A \mathcal{A} A，存在可忽略的函数 n e g l \mathsf{negl} negl使得，

Pr ⁡ [ P r i v K A , Π c p a ( n ) = 1 ] ≤ 1 2 + n e g l ( n )
\Pr\left[\mathsf{PrivK}^{\mathsf{cpa}}_{\mathcal{A},\Pi}(n)=1\right] \le
\frac{1}{2} + \mathsf{negl}(n) Pr[PrivKA,Πcpa(n)=1]≤21+negl(n)

* 定理：CPA安全也是多重加密安全的。证明略。直觉上，CPA敌手比多重加密敌手更强大。

* 之前的方案也难以实现CPA安全；

* 多重加密安全意味着CPA安全？（作业）显然是否定的。那么，思考两种安全定义的区别成为解题的关键。

操作模式

伪随机函数PRF

伪随机函数（ Pseudorandom Function ）概念

* 为了实现CPA安全，之前的PRG提供的随机性不够用了，需要新的数学工具为加密提供额外的随机性。为此引入伪随机函数（PRF），是对伪PRG的泛化：PRG从一个种子生成一个随机串，PRF从一个key生成一个函数；
* 带密钥的函数 **Keyed function** F : { 0 , 1 } ∗ × { 0 , 1 } ∗ → { 0 , 1 } ∗ F : \\{0,1\\}^* \times \\{0,1\\}^* \to \\{0,1\\}^* F:{0,1}∗×{0,1}∗→{0,1}∗
  * F k : { 0 , 1 } ∗ → { 0 , 1 } ∗ F_k : \\{0,1\\}^* \to \\{0,1\\}^* Fk:{0,1}∗→{0,1}∗,  F k ( x ) = def F ( k , x ) F_k(x) \overset{\text{def}}{=} F(k,x) Fk(x)=defF(k,x)
  * 两个输入到一个输出，看上去像，但不是加密函数；输入key，得到一个一输入到一输出的函数；
* 查表 **Look-up table** f f f:  { 0 , 1 } n → { 0 , 1 } n \\{0,1\\}^n \to \\{0,1\\}^n {0,1}n→{0,1}n 需要多少比特信息存储？ 
  * 查表是一个直接描述输入与输出间映射的表格，一个条目对应一个输入与一个输出；当该映射是随机产生的，是一个真随机函数；
* 函数族 **Function family** F u n c n \mathsf{Func}_n Funcn: 包含所有函数  { 0 , 1 } n → { 0 , 1 } n \\{0,1\\}^n \to \\{0,1\\}^n {0,1}n→{0,1}n.  ∣ F u n c n ∣ = 2 n ⋅ 2 n |\mathsf{Func}_n| = 2^{n\cdot2^n} ∣Funcn∣=2n⋅2n
  * 一个PRF是函数族中一个子集，key确定下的PRF是函数族中一个元素，一个查表是函数族中一个元素；
* 长度保留 **Length Preserving** :  ℓ k e y ( n ) = ℓ i n ( n ) = ℓ o u t ( n ) = n \ell_{key}(n) = \ell_{in}(n) = \ell_{out}(n) = n ℓkey(n)=ℓin(n)=ℓout(n)=n；密钥长度与函数输入、输出长度相同为 n n n；没有特殊说明时，只讨论长度保留的函数；

伪随机函数定义

* 直觉上，一个PRF生成的带密钥的函数与从函数族中随机选择的真随机函数（查表）之间是不可区分的；然而，一个真随机函数具有指数长度，无法“预先生成”，只能“on-the-fly”（边运行、边生成）的使用，引入一个对函数 O \mathcal{O} O的确定性的预言机访问（oracle access） D O D^\mathcal{O} DO。
* 这里的预言机是一个抽象的函数。访问预言机，就是给出任意输入，得到该函数的输出。访问预言机的能力不包括了解正在访问的预言机具体内部构造。
* 一个带密钥的函数是一个伪随机函数（PRF），对任意PPT区分器 D D D， ∣ Pr ⁡ [ D F k ( ⋅ ) ( 1 n ) = 1 ] − Pr ⁡ [ D f ( ⋅ ) ( 1 n ) = 1 ] ∣ ≤ n e g l ( n ) \left|\Pr[D^{F_k(\cdot)}(1^n)=1] - \Pr[D^{f(\cdot)}(1^n)=1]\right| \le \mathsf{negl}(n)  Pr[DFk(⋅)(1n)=1]−Pr[Df(⋅)(1n)=1] ≤negl(n)，其中 f f f是 F u n c n \mathsf{Func}_n Funcn中随机函数。 
  * 这里区分器 D D D是一个算法，可以访问预言机，但并不知道预言机背后是什么。
  * 这里不可区分性关键是，对真随机查表和伪随机函数，区分器输出相同结果概率的差异。区分器输出1或0本身没有，也无需，有特定语义。
* PRF和PRG的关系在后面会学习，可以由PRG来构造PRF。

PRF例题

* 问题一个固定长度的一次一密方案是一个PRF吗？
* 对于一个PRF，在密钥保密和没有预言机访问时，给指定输入，能以不可忽略的概率猜测输出相关信息吗？
* 如果是PRF，则给出该函数与查表的相似性；否则，给出一个区分器可以区分出该函数不是随机的。

以PRF实现CPA安全

* 新随机串  r r r，每次新生成一个随机串；
* F k ( r ) F_k(r) Fk(r):  ∣ k ∣ = ∣ m ∣ = ∣ r ∣ = n |k| = |m| = |r| = n ∣k∣=∣m∣=∣r∣=n. 长度保留；
* G e n \mathsf{Gen} Gen:  k ∈ { 0 , 1 } n k \in \\{0,1\\}^n k∈{0,1}n.
* E n c \mathsf{Enc} Enc:  s : = F k ( r ) ⊕ m s := F_k(r)\oplus m s:=Fk(r)⊕m,  c : = < r , s > c := \left<r, s\right> c:=⟨r,s⟩. 密文包括两部分新随机串，以及异或输出；
* D e c \mathsf{Dec} Dec:  m : = F k ( r ) ⊕ s m := F_k(r)\oplus s m:=Fk(r)⊕s.
* 定理：上述方案是CPA安全的。

从PRF到CPA安全的证明

* 思路：从PRF的区分器算法 D \mathcal{D} D规约到加密方案敌手算法 A \mathcal{A} A，区分器 D \mathcal{D} D作为敌手 A \mathcal{A} A的挑战者，敌手 A \mathcal{A} A实验成功时区分器 D \mathcal{D} D输出1。分两种情况，当输入真随机函数 f f f时，相当于一次一密；当输入伪随机函数 F k F_k Fk时，为加密方案。
* 规约： D \mathcal{D} D输入预言机，输出一个比特； A \mathcal{A} A的加密预言机访问通过 D \mathcal{D} D的预言机 O \mathcal{O} O来提供， c : = < r , O ( r ) ⊕ m > c := \left<r, \mathcal{O}(r) \oplus m \right> c:=⟨r,O(r)⊕m⟩； D \mathcal{D} D输出1，当 A \mathcal{A} A在实验中成功。 
  * 这里有两个预言机： D \mathcal{D} D访问的预言机 O \mathcal{O} O， A \mathcal{A} A访问的加密预言机 E n c k \mathsf{Enc}_k Enck，后者不能直接访问前者的预言机。

从PRF到CPA安全的证明（续）

* 考虑真随机函数 f f f的情况，分析不可区分实验成功概率 Pr ⁡ [ P r i v K A , Π ~ c p a ( n ) = 1 ] = Pr ⁡ [ B r e a k ] \Pr[\mathsf{PrivK}_{\mathcal{A},\tilde{\Pi}}^{\mathsf{cpa}}(n) = 1] = \Pr[\mathsf{Break}] Pr[PrivKA,Π~cpa(n)=1]=Pr[Break]。敌手 A \mathcal{A} A访问加密预言机可以获得多项式 q ( n ) q(n) q(n)个明文与密文对的查询结果并得到随机串和pad { < r i , f ( r i ) > } \\{ \left< r_i, f(r_i) \right> \\} {⟨ri,f(ri)⟩}；当收到挑战密文 c = < r c , s : = f ( r c ) ⊕ m b > c=\left<r_c, s:=f(r_c)\oplus m_b\right> c=⟨rc,s:=f(rc)⊕mb⟩时，根据之前查询结果中随机串是否与挑战密文中随机串相同，分为两种情况：

  * 当有相同随机串时，根据 r r r可以得到 f ( r c ) f(r_c) f(rc)， m b = f ( r c ) ⊕ s m_b=f(r_c)\oplus s mb=f(rc)⊕s，但这种情况发生的概率 q ( n ) / 2 n q(n)/2^n q(n)/2n是可忽略的；
  * 当没有相同随机串时，输出是随机串，相当于一次一密，成功概率=1/2；
* Pr ⁡ [ D F k ( ⋅ ) ( 1 n ) = 1 ] = Pr ⁡ [ P r i v K A , Π c p a ( n ) = 1 ] = 1 2 \+ ε ( n ) . \Pr[D^{F_k(\cdot)}(1^n)=1] = \Pr[\mathsf{PrivK}_{\mathcal{A},\Pi}^{\mathsf{cpa}}(n) = 1] = \frac{1}{2} + \varepsilon(n). Pr[DFk(⋅)(1n)=1]=Pr[PrivKA,Πcpa(n)=1]=21+ε(n).

* Pr ⁡ [ D f ( ⋅ ) ( 1 n ) = 1 ] = Pr ⁡ [ P r i v K A , Π ~ c p a ( n ) = 1 ] = Pr ⁡ [ B r e a k ] ≤ 1 2 \+ q ( n ) 2 n . \Pr[D^{f(\cdot)}(1^n)=1] = \Pr[\mathsf{PrivK}_{\mathcal{A},\tilde{\Pi}}^{\mathsf{cpa}}(n) = 1] = \Pr[\mathsf{Break}] \le \frac{1}{2} + \frac{q(n)}{2^n}. Pr[Df(⋅)(1n)=1]=Pr[PrivKA,Π~cpa(n)=1]=Pr[Break]≤21+2nq(n).

* Pr ⁡ [ D F k ( ⋅ ) ( 1 n ) = 1 ] − Pr ⁡ [ D f ( ⋅ ) ( 1 n ) = 1 ] ≥ ε ( n ) − q ( n ) 2 n . \Pr[D^{F_k(\cdot)}(1^n)=1] - \Pr[D^{f(\cdot)}(1^n)=1] \ge \varepsilon(n) - \frac{q(n)}{2^n}. Pr[DFk(⋅)(1n)=1]−Pr[Df(⋅)(1n)=1]≥ε(n)−2nq(n). 根据伪随机函数定义， ε ( n ) \varepsilon(n) ε(n) 是可忽略的.

* 小结：通过规约将 A \mathcal{A} A的不可区分实验成功的概率与 D D D的区分器实验输出1的概率建立等式；分析输入真随机函数预言机时 D D D输出1的概率（即不可区分实验成功概率）是1/2+一个可忽略函数；根据PRF的定义，输入伪随机函数预言机时 D D D输出1的概率（1/2+ ε ( n ) \varepsilon(n) ε(n)）与输入真随机函数预言机时 D D D输出1的概率（1/2）的差异时可忽略的。

CPA安全例题

* E n c k ( m ) = P R G ( k ∥ r ) ⊕ m \mathsf{Enc}_k(m) = PRG(k\|r) \oplus m Enck(m)=PRG(k∥r)⊕m,  r r r 是新的随机串。这是CPA安全的吗？
* 从PRF到CPA安全：变长消息
* 对于任意长度消息  m = m 1 , … , m ℓ m = m_1, \dots , m_{\ell} m=m1,…,mℓ， c : = < r 1 , F k ( r 1 ) ⊕ m 1 , r 2 , F k ( r 2 ) ⊕ m 2 , … , r ℓ , F k ( r ℓ ) ⊕ m ℓ > c := \left< r_1, F_k(r_1) \oplus m_1, r_2, F_k(r_2) \oplus m_2, \dots, r_\ell, F_k(r_\ell) \oplus m_\ell\right> c:=⟨r1,Fk(r1)⊕m1,r2,Fk(r2)⊕m2,…,rℓ,Fk(rℓ)⊕mℓ⟩
* 推论：如果 F F F是一个 PRF，那么  Π \Pi Π 对任意长度消息是 CPA 安全的。
* 问题：这个方案有什么缺点？
* 有效性:  ∣ c ∣ = 2 ∣ m ∣ |c| = 2|m| ∣c∣=2∣m∣. 密文长度是明文长度的二倍，并且需要大量的真随机串。

伪随机排列PRP

伪随机排列（ Pseudorandom Permutations ）

* 为了提高对任意长度消息加密的效率，以及更高级的加密基础工具，学习伪随机排列PRP的概念；

* 双射 **Bijection** :  F F F 是一到一的（一个输入对应一个唯一输出）且满射（覆盖输出集中每个元素）；

* 排列 **Permutation** : 一个从一个集合到自身的双射函数；

* 带密钥的排列 **Keyed permutation** :  ∀ k , F k ( ⋅ ) \forall k, F_k(\cdot) ∀k,Fk(⋅)是排列；类似带密钥的函数；

* F F F 是一个双射  ⟺ F − 1 \iff F^{-1} ⟺F−1 是一个双射；函数和逆函数都是双射；

* 定义：一个有效的带密钥的排列  F F F 是PRP，如果对于任意PPT的区分器 D D D，

∣ Pr ⁡ [ D F k ( ⋅ ) , F k − 1 ( ⋅ ) ( 1 n ) = 1 ] − Pr ⁡ [ D f ( ⋅ ) , f − 1
( ⋅ ) ( 1 n ) = 1 ] ∣ ≤ n e g l ( n )
\left|\Pr[D{F_k(\cdot),F_k{-1}(\cdot)}(1^n)=1] -
\Pr[D{f(\cdot),f{-1}(\cdot)}(1^n)=1]\right| \le \mathsf{negl}(n)
Pr[DFk(⋅),Fk−1(⋅)(1n)=1]−Pr[Df(⋅),f−1(⋅)(1n)=1] ≤negl(n)

* 问题：一个PRP也是一个PRF吗？

PRP例题

* 对1比特的PRP、PRF的分析；
* 交换引理：如果  F F F 是一个 PRP 并且  ℓ i n ( n ) ≥ n \ell_{in} (n) \ge n ℓin(n)≥n，那么  F F F 也是一个 PRF。 
  * 一个随机排列和一个查表是不可取分的，PRP和随机排列不可取分，因此，PRP和查表是不可取分的。

操作模式概念（ Modes of Operation ）

* 操作模式是使用PRP或PRF来加密任意长度消息的方法；
* 操作模式是从PRP或PRF来构造一个PRG的方法；
* 将一个消息分成若干等长的块（分组，block），每个块以相似方式处理；

Electronic Code Book (ECB) 模式

* 在窃听者出现时，是否是不可区分的？
* F F F 可以是任意PRF吗？

对ECB的攻击

* 为什么仍然可以识别企鹅？

Cipher Block Chaining (CBC) 模式

* I V IV IV初始向量，一个新的随机串；
* 是CPA的吗？可并行化吗？F可以是任意PRF吗？

Output Feedback (OFB) Mode 模式

* 是CPA安全吗？可并行化吗？F可以是任意PRF吗？

Counter (CTR) Mode 模式

* c t r ctr ctr是一个初始向量，并且逐一增加；
* 是CPA安全吗？可并行化吗？F可以是任意PRF吗？

CTR模式是CPA安全
![在这里插入图片描述](https://img-
blog.csdnimg.cn/direct/57b0db18ae3e4ddda0c32c49a5c00a8a.png)

* 定理：如果 F F F是一个PRF，那么随机CTR模式是CPA安全的。

* 证明：其安全性与之前基于PRF的CPA安全证明类似，从PRF的伪随机假设规约到CPA安全加密方案。其中，对 c t r ctr ctr的安全性直觉在于， c t r ctr ctr也是在加密前不可预测的，且每个块所用 c t r ctr ctr都是不同的；

* 当加密预言机是由真随机查表构成时，敌手多次访问加密预言机得到的 c t r ctr ctr序列与挑战密文的 c t r ctr ctr序列之间有重叠的概率 2 q ( n ) 2 2 n \frac{2q(n)^2}{2^n} 2n2q(n)2是可以忽略的；若没有重叠，则相当于一次一密；

* 规约与之前证明基于PRF的CPA安全加密方案一样，证明过程也类似。

初始向量不应该可预测

* 如果 I V IV IV是可预测的，那么CBC/OFB/CTR模式不是CPA安全的。
* 为什么？（作业）
* 在SSL/TLS 1.0中的漏洞：记录 # i \\#i #i的 I V IV IV是上一个记录 # ( i − 1 ) \\#(i-1) #(i−1)的密文块。
* OpenSSL中API：需要用户输入 I V IV IV，但 I V IV IV应在函数内实现。当 I V IV IV不充分随机时不安全。

非确定性加密

* 有三种通用的实现CPA安全的非确定性加密方法：
* 随机化的： r r r随机生成，如构造5；需要更多熵，长密文
* 有状态的： r r r为计数器，如CTR模式；需要通信双方同步计数器
* 基于Nonce的： r r r只用一次；需要保证只用一次，长密文

CCA安全加密方案

选择密文攻击 Chosen-Ciphertext Attacks (CCA)

* CCA不可区分实验  P r i v K A , Π c c a ( n ) \mathsf{PrivK}^{\mathsf{cca}}_{\mathcal{A},\Pi}(n) PrivKA,Πcca(n):

  1. 挑战者生成密钥  k ← G e n ( 1 n ) k \gets \mathsf{Gen}(1^n) k←Gen(1n)；（为了下一步的预言机）
  2. A \mathcal{A} A 被给予输入  1 n 1^n 1n 和对加密函数  E n c k ( ⋅ ) \mathsf{Enc}_k(\cdot) Enck(⋅)和解密函数 D e c k ( ⋅ ) \mathsf{Dec}_k(\cdot) Deck(⋅)的 **预言机访问（oracle access）** A E n c k ( ⋅ ) \mathcal{A}^{\mathsf{Enc}_k(\cdot)} AEnck(⋅) 和  A D e c k ( ⋅ ) \mathcal{A}^{\mathsf{Dec}_k(\cdot)} ADeck(⋅)，输出相同长度  m 0 , m 1 m_0, m_1 m0,m1 ；
  3. 挑战者生成随机比特  b ← { 0 , 1 } b \gets \\{0,1\\} b←{0,1}，将挑战密文  c ← E n c k ( m b ) c \gets \mathsf{Enc}_k(m_b) c←Enck(mb) 发送给  A \mathcal{A} A；
  4. A \mathcal{A} A 继续对除了挑战密文 c c c之外的预言机的访问，输出 b ′ b' b′；如果 b ′ = b b' = b b′=b，则 A \mathcal{A} A成功 P r i v K A , Π c c a = 1 \mathsf{PrivK}^{\mathsf{cca}}_{\mathcal{A},\Pi}=1 PrivKA,Πcca=1，否则 0。

定义：一个加密方案是CCA安全的，如果实验成功的概率与1/2的差异是可忽略的。

理解CCA安全

* 在现实世界中，敌手可以通过影响被解密的内容来实施CCA。如果通信没有认证，那么敌手可以以通信参与方的身份来发送特定密文。下一页有具体真实案例。

* CCA安全性意味着“non-malleability”（不可锻造性，即改变但不毁坏），不能修改密文来获得新的有效密文。

* 之前的方案中没有CCA安全，因为都不是不可锻造。

* 对基于PRF的CPA安全加密方案的CCA攻击：

  * A \mathcal{A} A 获得挑战密文  c = < r , F k ( r ) ⊕ m b > c = \left<r, F_k(r)\oplus m_{b}\right> c=⟨r,Fk(r)⊕mb⟩，并且查询与 c c c只相差了一个翻转的比特的密文 c ′ c' c′，那么

m ′ = c ′ ⊕ F k ( r ) m’ = c’ \oplus F_k® m′=c′⊕Fk® 应该与 m b m_{b} mb
除了什么之外都相同？（见下方的补充）

* 问题：上述操作模式也不是CCA安全的（作业）

* 由此，可以总结出CCA下敌手的常用策略：

  * 修改挑战密文 c c c为 c ′ c' c′，并查询解密预言机得到 m ′ m' m′
  * 根据关系，由 m ′ m' m′来猜测被加密明文 m b m_b mb

补充

在这个情况下， A \mathcal{A} A 获得了挑战密文 c = < r , F k ( r ) ⊕ m b > c = \left<r,
F_k®\oplus m_{b}\right> c=⟨r,Fk®⊕mb⟩ 并查询了一个只在一个比特上与 c c c 不同的密文 c ′ c’
c′。我们来分析一下 m ′ = c ′ ⊕ F k ( r ) m’ = c’ \oplus F_k® m′=c′⊕Fk® 与 m b
m_{b} mb 的关系。

首先，我们明确 c c c 的构成：

c c c 包含两个部分：一个随机数 r r r 和使用密钥 k k k 的函数 F k ( r ) F_k® Fk® 与明文 m b m_{b} mb 的异或结果。
因此， c = < r , F k ( r ) ⊕ m b > c = \left<r, F_k®\oplus m_{b}\right> c=⟨r,Fk®⊕mb⟩。

现在，如果 A \mathcal{A} A 查询了一个与 c c c 只在一个比特上不同的密文 c ′ c’ c′，那么 c ′ c’ c′
也可以写成两部分，但其中一部分与 c c c 有一个比特的差异。这个差异可以在 r r r 部分，也可以在 F k ( r ) ⊕ m b
F_k®\oplus m_{b} Fk®⊕mb 部分。

当 A \mathcal{A} A 计算 m ′ = c ′ ⊕ F k ( r ) m’ = c’ \oplus F_k®
m′=c′⊕Fk® 时，他们实际上是在解开 F k ( r ) ⊕ m b F_k®\oplus m_{b} Fk®⊕mb
的异或操作。这是因为异或操作是可逆的，且当两次使用相同的值时会取消彼此的效果（即 A ⊕ B ⊕ B = A A \oplus B \oplus B =
A A⊕B⊕B=A）。

因此，如果 c ′ c’ c′ 的变化发生在 F k ( r ) F_k® Fk® 部分，则 m ′ m’ m′ 将与 m b m_{b}
mb 完全相同，因为 F k ( r ) F_k® Fk® 部分的变化被异或操作取消了。但如果变化发生在 r r r
部分，则这个变化不会影响到 F k ( r ) ⊕ m b F_k®\oplus m_{b} Fk®⊕mb 部分，因此 m ′ m’ m′
将与 m b m_{b} mb 在一个比特上不同。

综上所述， m ′ m’ m′ 与 m b m_{b} mb 将在以下方面相同：

如果变化发生在 F k ( r ) F_k® Fk® 部分，那么 m ′ m’ m′ 与 m b m_{b} mb 完全相同。
如果变化发生在 r r r 部分，那么 m ′ m’ m′ 与 m b m_{b} mb 除了那个翻转的比特之外都相同。

填充预言机Padding-Oracle攻击真实案例

Padding-Oracle（填充预言机）攻击真实案例

* CAPTCHA服务商为Web网站提供验证用户是否为人类的服务。为此，一个CAPTCHA服务器与Web服务器间事先共享一个密钥 k k k，服务工作原理如下： 
  1. 当Web服务器验证用户是否为人类时，生成一个消息 w w w并以 k k k加密，向用户发送一个密文 E n c k ( w ) Enc_k(w) Enck(w)；
  2. 用户将密文 E n c k ( w ) Enc_k(w) Enck(w)转发给CAPTCHA服务器；（可实施填充预言机攻击）
  3. CAPTCHA服务器用密钥 k k k将密文解密，根据解密结果返回给用户信息：一个由 w w w生成的图像，或者坏填充错误；
  4. 用户根据图像获得  w w w 并将  w w w 发送给Web服务器。
* 在第2步，当恶意用户可以利用CAPTCHA服务器会返回给用户坏填充错误这一漏洞，来实施填充错误攻击。

Padding-Oracle（填充预言机）攻击

* 在PKCS #5 padding（填充）标准中，为了将一个消息的长度“填充”到块长度的整数倍，在最后一个块中填充 b b b个字节的 b b b；必要时，添加一个哑块（dummy block，不包含消息的一个填充块）。存在一种攻击手段：当填充错误时，解密服务器返回一个“坏填充错误”，这相当于提供了一个解密预言机，最终可以获得整个明文；
* 具体攻击原理： 
  * 更改密文（包含 I V IV IV部分）并发送给解密服务器；
  * 一旦触发了“坏填充错误”，则说明对密文的更改导致了填充部分内容的更改；否则，对密文的更改导致了原明文部分的更改；
  * 通过仔细修改密文来控制填充部分，从而获得消息长度和内容。

填充预言机攻击：获得消息长度

* 攻击的第一步判断消息是否为空：在单个块的CBC中，通过更改 I V IV IV的首个字节，攻击者能够获知是否 m m m是否为空。因为如果 m m m是空的话，更改 I V IV IV首个字节将更改解密出的填充内容，解密服务器就会返回坏填充错误（1比特信息），具体分析如下： 
  * 如果 m m m是空的，那么明文会添加一个哑块 { b } b \\{b\\}^b {b}b；
  * PRP的输入为 I V ⊕ { b } b IV\oplus \\{b\\}^b IV⊕{b}b；设 I V IV IV的首个字节为 x x x，则PRP的输入为 ( x ⊕ b ) ∥ ( { ⋅ } b − 1 ⊕ { b } b − 1 ) (x \oplus b) \| (\\{\cdot\\}^{b-1} \oplus \\{b\\}^{b-1}) (x⊕b)∥({⋅}b−1⊕{b}b−1)；
  * 将 I V IV IV的首个字节从 x x x改成 y y y变为  y ∥ ( { ⋅ } b − 1 ) y \| (\\{\cdot\\}^{b-1}) y∥({⋅}b−1)，不改变 c 1 c_1 c1解密得到的PRP的输入不会变，而解密出的明文会改变为  ( x ⊕ y ⊕ b ) ∥ { b } b − 1 (x \oplus y \oplus b) \| \\{b\\}^{b-1} (x⊕y⊕b)∥{b}b−1；
  * 上述明文首个字节一定不是 b b b，这是填充格式错误，会触发服务器返回错误；
  * 如果上面的尝试没有触发错误，那么说明消息非空；下一步，发现消息长度是否为1字节，方法与上一步一样，区别在于只改变 I V IV IV的第2个字节；如此继续，获得消息的长度；（作业）

填充预言机攻击：获得消息内容

* 一旦获得消息的长度，也就知道了填充的长度 b b b，采用下面的方法来获得消息的最后一个字节内容，进而获得整个消息；
* 更改密文中倒数第二块，来获得消息的最后一个字节 s s s；
* 明文的最后一个块  m l a s t = ⋯ s ∥ { b } b m_{last} = \cdots s \| \\{b\\}^{b} mlast=⋯s∥{b}b，密文的倒数第二个块  c l a s t − 1 = ⋯ t ∥ { ⋅ } b c_{last-1} = \cdots t \| \\{\cdot \\}^{b} clast−1=⋯t∥{⋅}b；
* 最后一块的PRP输入为 c l a s t − 1 ⊕ m l a s t = ⋯ ( s ⊕ t ) ∥ ( { b } b ⊕ { ⋅ } b ) c_{last-1} \oplus m_{last} = \cdots (s \oplus t) \| (\\{b\\}^b \oplus \\{\cdot \\}^{b}) clast−1⊕mlast=⋯(s⊕t)∥({b}b⊕{⋅}b)；
* 敌手更改  c l a s t − 1 c_{last-1} clast−1 为  c l a s t − 1 ′ = ⋯ u ∥ ( { ⋅ } b ⊕ { b } b ⊕ { b \+ 1 } b ) c_{last-1}' = \cdots u \| (\\{\cdot \\}^{b} \oplus \\{b\\}^{b} \oplus \\{b+1\\}^{b}) clast−1′=⋯u∥({⋅}b⊕{b}b⊕{b+1}b)；其中， u u u是敌手猜测的某个字节；
* 解密获得最后一块明文 m l a s t ′ = c l a s t − 1 ⊕ m l a s t ⊕ c l a s t − 1 ′ = ⋯ ( s ⊕ t ⊕ u ) ∥ { b \+ 1 } b m'_{last} = c_{last-1} \oplus m_{last} \oplus c_{last-1}' = \cdots (s \oplus t \oplus u)\| \\{ b+1 \\}^b mlast′=clast−1⊕mlast⊕clast−1′=⋯(s⊕t⊕u)∥{b+1}b；
* 如果没有返回坏填充错误，那么意味着填充了 b \+ 1 b+1 b+1个字节的 b \+ 1 b+1 b+1，所以  s ⊕ t ⊕ u = ( b \+ 1 ) s \oplus t \oplus u = (b+1) s⊕t⊕u=(b+1) ，而  s = t ⊕ u ⊕ ( b \+ 1 ) s = t \oplus u \oplus (b+1) s=t⊕u⊕(b+1) 。

总结

* 略

学习网络安全技术的方法无非三种:

第一种是报网络安全专业，现在叫网络空间安全专业，主要专业课程:程序设计、计算机组成原理原理、数据结构、操作系统原理、数据库系统、
计算机网络、人工智能、自然语言处理、社会计算、网络安全法律法规、网络安全、内容安全、数字取证、机器学习，多媒体技术，信息检索、舆情分析等。

第二种是自学，就是在网上找资源、找教程，或者是想办法认识一-
些大佬，抱紧大腿，不过这种方法很耗时间，而且学习没有规划，可能很长一段时间感觉自己没有进步，容易劝退。

如果你对网络安全入门感兴趣，那么你需要的话可以点击这里
👉[网络安全重磅福利：入门&进阶全套282G学习资源包免费分享！](https://mp.weixin.qq.com/s/BWb9OzaB-
gVGVpkm161PMw)

第三种就是去找培训。

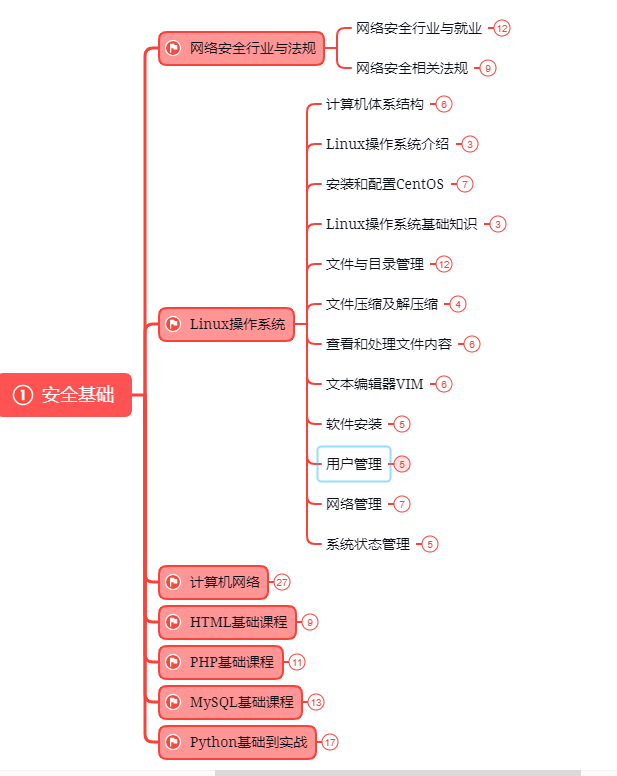
![image.png](https://img-
blog.csdnimg.cn/img_convert/58bec76876e81d23709a090231e9e0bf.png)

接下来，我会教你零基础入门快速入门上手网络安全。

网络安全入门到底是先学编程还是先学计算机基础？这是一个争议比较大的问题，有的人会建议先学编程，而有的人会建议先学计算机基础，其实这都是要学的。而且这些对学习网络安全来说非常重要。但是对于完全零基础的人来说又或者急于转行的人来说，学习编程或者计算机基础对他们来说都有一定的难度，并且花费时间太长。

第一阶段：基础准备 4周~6周

这个阶段是所有准备进入安全行业必学的部分，俗话说：基础不劳，地动山摇
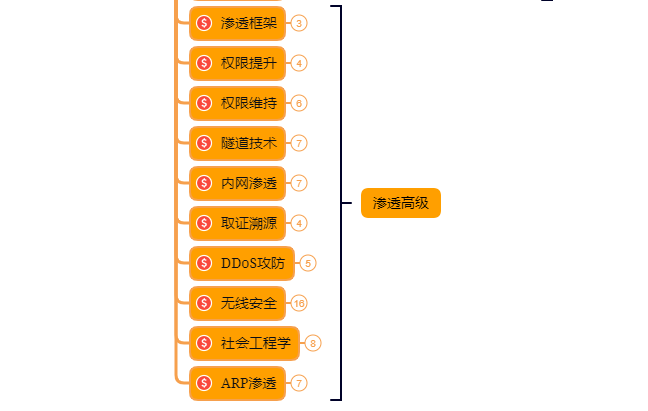
![image.png](https://img-
blog.csdnimg.cn/img_convert/44dd65e103a3ce90b8500717e19b108d.png)

第二阶段：web渗透

学习基础时间：1周 ~ 2周：

① 了解基本概念：（SQL注入、XSS、上传、CSRF、一句话木马、等）为之后的WEB渗透测试打下基础。
② 查看一些论坛的一些Web渗透，学一学案例的思路，每一个站点都不一样，所以思路是主要的。
③ 学会提问的艺术，如果遇到不懂得要善于提问。
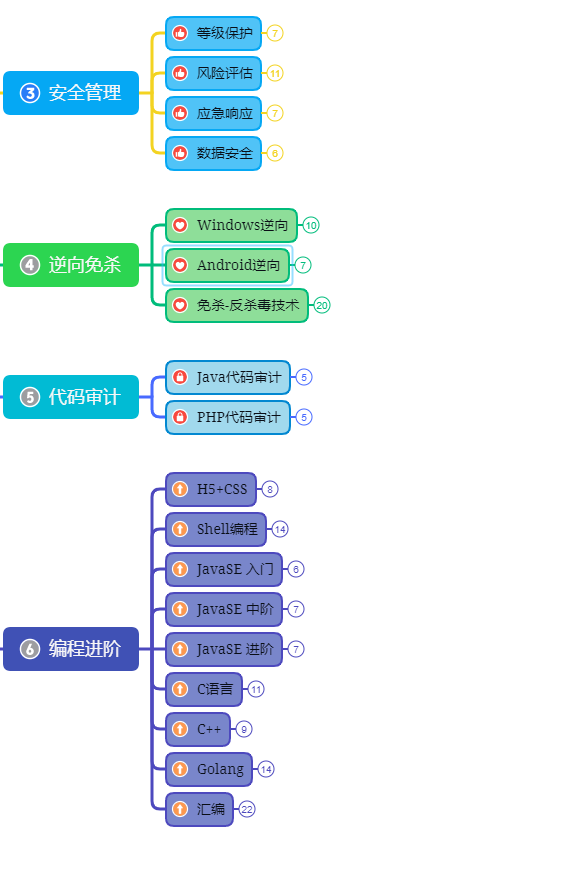
![image.png](https://img-
blog.csdnimg.cn/img_convert/442b7a338582713846cc447ecff221bd.png)

配置渗透环境时间：3周 ~ 4周：

① 了解渗透测试常用的工具，例如（AWVS、SQLMAP、NMAP、BURP、中国菜刀等）。
② 下载这些工具无后门版本并且安装到计算机上。
③ 了解这些工具的使用场景，懂得基本的使用，推荐在Google上查找。

渗透实战操作时间：约6周：

① 在网上搜索渗透实战案例，深入了解SQL注入、文件上传、解析漏洞等在实战中的使用。
② 自己搭建漏洞环境测试，推荐DWVA，SQLi-labs，Upload-labs，bWAPP。
③ 懂得渗透测试的阶段，每一个阶段需要做那些动作：例如PTES渗透测试执行标准。
④ 深入研究手工SQL注入，寻找绕过waf的方法，制作自己的脚本。
⑤ 研究文件上传的原理，如何进行截断、双重后缀欺骗(IIS、PHP)、解析漏洞利用（IIS、Nignix、Apache）等，参照：上传攻击框架。
⑥ 了解XSS形成原理和种类，在DWVA中进行实践，使用一个含有XSS漏洞的cms，安装安全狗等进行测试。
⑦ 了解一句话木马，并尝试编写过狗一句话。
⑧ 研究在Windows和Linux下的提升权限，Google关键词：提权
![image.png](https://img-
blog.csdnimg.cn/img_convert/820f500673a4a0a2432e6c3d7e2ba80e.png)
以上就是入门阶段