深入理解计算机系统之浮点数

一、什么是浮点数

了解浮点数这个概念前，先要了解什么是定点数，定点数的概念为：

定点表示即约定机器数中的小数点位置是固定不变的，小数点不再使用“.”表示，而是约定它的位置，即在固定 bit 下，约定小数点的位置，然后把整数部分和小数部分分别转换为二进制，就是定点数的结果。

而浮点数的概念即是与定点数相反的，浮点数的小数点位置不是固定的，当然这是一句废话。

接下来重点来了，浮点数小数点的浮动性怎么体现呢？

这里就引入一个名为科学计数法的概念：（十进制下）

科学记数法是一种记数的方法。 把一个数表示成a与10的n次幂相乘的形式

（1≤|a|<10，a不为分数形式，n为整数），这种记数法叫做 科学记数法。

例如：十进制小数 1.2345 我们可以用多种形式的计数法表达这一个数：

...

诸如此类的形式，我们会发现不同表达方式下，小数点的位置都是不同的，我们可以由10的多少次幂(后会说明此为阶码)来移动这个小数点，但表达的都是同一个数，浮点数的概念由此而来。

上述的科学计数法是基于十进制下表现的，我们以此进行展开，同样可以得到其他进制下的科学计数法的表达方式。

比如二进制下小数 10.111 我们用二进制科学计数法表达它：

...

现在我们已经对浮点数的概念应该已经有了一个比较理性的认识.

二、计算机如何表达浮点数

        我们知道在计算机内所有的指令和储存都是基于二进制的 01 串构成，那么浮点数也不例外，根据上文，我们可以科学计数法表达所有的小数，它的形式如下：

即 浮点数 = 基数 * 进制 ^ 幂次

化为更一般的形式为：
 

（公式1）

其中 S 表示符号(Symbol)， M 表示为尾数(Mantissa)(即小数点应该放在哪位，对应于某一种浮点数的科学计数法的表示方式)，R 表示为基数(Radix)(不同进制下的阶数不同，如十进制下 R = 10， 二进制下 R = 2)，E 表示的就是阶码(Exponent)(其实就是指数啦)。

 例：      (十进制)

                原数 = （-1）^ 符号 * 尾数 * 10 ^ 阶码

————分割线（可以直接跳到下一个分割线下面）

通用形式我们表达出来了，计算机如何表达他们呢？接下来的过程有点抽象，但是我们只需要明白一点，计算机只是一个计算工具，它所有表达出的功能都只是我们人为的对其解读数据方式进行规范，所有命令在计算机内的本质都是 01 串。

比如说 1 ，我们可以对 1 解读为 1 个 10，1 个 100，...，那 1 具体表达什么我们就需要从特定的场合中去理解，这就是一个抽象的过程。懂得了这里，那么下面的规则也就不难理解了。 

————分割线

        我们知道计算机储存一个 (int) 型整数是需要 32 位 bit 进行储存，如果32位不够用我们还有64位 bit 的 (long) 型整数；而浮点数也是用同样的方式去存储的，它就分为了32位的 float (单精度)，和64位的double (双精度)这两种类型 (此处的概念源于第三节浮点数标准)。

下面先给出二进制和十进制小数转化的概念，为了理解方便，依旧采用类比的方式。

对于十进制数（1.12）我们可以把这个数分为整数部分和小数部分

那么二进制数（11.11）同样可以分为整数和小数部分

我们知道整数部分二进制转化为十进制是通过给每一个二进制位赋权相加而来

如：二进制数 (11) 转化为十进制：

那么小数点后的数 ( .11) 我们同样是通过赋权方式将这个二进制小数转化为十进制：

那么对于二进制小数（11.01）转化为十进制就有：

我们可以发现，二进制并不能非常精确的表达十进制数，它能表达的小数只能由二的负次幂组合而成，下面给出每一位二进制小数位对比于十进制：

...

所以想完全精确地表达十进制小数诸如 (10.333) 这类型的整数是不可能的，那么为了缩小表达的误差，我们只能划分更多尾数位去表达这个数减小误差，而尾数的位数变多，就会导致阶码的位数变小，即表示的范围变小（推论1）.

        回归正题，我们现在要用计算机的 32位bit （单精度）去表达一个小数，那么我们必须告诉计算机一个解读二进制串的规则，否则计算机就单纯只能表达01串；根据科学计数法的公式1，我们可以知道我们需要用一个 bit 去表达符号位(S)，那么我们需要多少位去表达它的尾数部分和它的阶数部分？

现在我们不妨规定：在32位下，我们用1位表示符号，10位表示整数，21位表示小数(规则1)，现在给出一个十进制小数，请你根据规则解读他为二进制串：

 

例：-10.25

整数部分：10 —— 对应二进制 1010

小数部分：0.25 —— 对应二进制 .01

符号部分：-1 —— 对应二进制符号位 1

得到二进制串 1010.01（符号位不在内）

写成科学计数法的形式 有下式：

得出 S = 1，M = 1.01001，E = 3 （注意此时的E是十进制下的表达，写入阶码段时要转换）

二进制下这三十二位表示为：

看看我们从十进制小数转化为二进制经历了什么：

十进制小数——划分部分——将对应部分转化为二进制——组合得到的各部分二进制串——运用科学计数法表达得到的二进制串——将对应的S，M，E写入32位串对应位置中——得到答案

是不是比较轻松？

完成这部分就代表了我们很轻易的就创造了一种可以交给计算去执行十进制小数转化为二进制小数的规则1，

那么接下来根据这个规则1学习将二进制转化为十进制吧！

为方便阅读，S，E，M之间我们用 " | " 符号分开

 例：1 | 0000 0000 11 | 1100...00

得到 S = 1，E = 3，M = 1.1（E为十进制形式）

由十进制下的科学计数法转化得到二进制串 1100.0

由二进制

整数部分 1100 —— 对应十进制 12

小数部分 0 —— 对应十进制0

符号位 1 —— 对应 负号

所以得到十进制整数 -12.0

经过二进制到十进制的转化，我们会发现这个过程就是十进制转化为二进制的逆过程（废话），了解这些，我们就基本掌握计算机在规则1下转化浮点数的过程了，吗？

        其实仔细的同学会发现我们的规则1非常的不完善！存在很多优化的方法，接下来就是很重要的完善方式，一定要理解。

完善1：

阶码的完善：

        我们会发现对于我们对于阶码的解读只存在正数，没有负数的表示，考虑一下，我们如果有负数的阶码能得到什么？能表达更小的数！即精度更高，下面给出解释；

        对于规则1来说，我们如果用10位阶码的最高位表达符号位，其他不变根据公式1可推出，我们能表达的整数范围变小了(从 ~  到   ~ )，但使得数的表达一下子多出了  的精确度。

        我们使用小数肯定是希望越精确越好，所以为了更高的小数精确度，我们会使得阶码的最高位为符号位，因此我们得到 E 的范围为( ~ ).

完善2：

精度的完善：

        对规则1来说当我们计算21位的 M (尾数)时，我们会发现它前面总会有一个1存在(特殊情况暂不考虑)，且我们总会把这一个1存进计算机里面，如果我们把这个 1 隐去，就能够很轻易的获得22位的精度，这种方式也叫隐含以 1 开头的表示。

...

        其实还能完善的有很多，但是要记住，以上只是我们个人设计的一种二进制串的解读方式，如果我们每个人对计算机设定的解读二进制串的方式不同的话，就会导致不同计算机之间的数据移植变得困难，且不同的解读方式根据推论1可知得到的精度和范围也有很大的差异。

为了减少不同规则之间转换的计算成本，我们需要一个统一的标准

三、浮点数标准

        1985年IEEE推出了统一的浮点数标准，并给出了两种浮点数的格式：
1.float单精度类型：符号位占1位，阶码占8位，尾数占23位

2.double双精度类型：符号位占1位，阶码占11位，尾数占52位

        不仅如此，IEEE为了使表达更精确，还给出了很多的完善规则：

如：

1.我们上面说的 隐含 1 开头的表示，都可以使上述两种浮点数尾数精度加1

2.推出规格化数和非规格化数

我们发现如果不是所有的小数都需要隐含开头的1，所以IEEE对两者规定如下：

规格化数：阶码位不全为 1，也不全为0的数称为规格化数

        类比我们之前创造且完善了一部分的规则1，这里IEEE对阶码段的解读方式和我们的不一样，IEEE规定阶码段表达的二进制数为无符号数，那我们读取这个数时最大值就变成了255，和我们未进行完善2的规则1相比是一样的，但是我们采取的是最高位置为符号位，IEEE则设置了一个偏置值(bias)，让 E = e - bias(在单精度下bias = 127, 双精度下为bias = 1023)，其中 e 等于我们读到的阶码二进制无符号数，这使得单精度下E的表达范围为(-126 ~ 127)(注意这里计算出的范围是去点全1和全0的E).

且隐含 1 开头的表示只对规格化数生效.

非规格化数：阶码位为全0的数表示为非规格化数

        非规格化数的存在是为了表达规格化数表达不了的更小的数，由于阶码全为0，类比于规格化数的表示，它的E应该有 E = - bias，这样的表达，但是IEEE却规定 E = 1 - bias，这样反直觉的设定且使其减小了一个精度的表达方式好像不符合常理，其实，多加的这个1提供了一种从非规格化数平滑的转化到规格化数的方式(下面有给出伪证明). 所以对于单精度的非规格化数E = -126 .

看到这里，我们会发现，啊这单精度的E的值不就在规格化E的表达范围里面吗？拿要这非规格化数有何用？

其实我们可以注意到，非规格化数给我们提供了一种表达0的方式，(由于我们为了多一个位的精度，隐去开头1造成的连锁反应)，因为规格化数隐去1的开头，所以其不能表达 0 这个数；且由于规格化隐去了1开头，那么我们想用规格化数表达 非常趋近于0的数 的话显然就不是特别理想了，而非规格化能表达没有开头1的这种数，即有无限趋近0的数的这种属性(在csapp种称这种属性为逐渐下溢，感觉不讲人话)

那么有规格化和非规格化这两个数合在一起，我们就能表达非常精确的小数了，那两者合在一起取交集，如果我们之前非规格化数的E没有加1，计算结果为-127的化，虽然说精度范围增加了一位，但是由于规格化数E的范围只为(-126 ~ 127)，这就代表我们取两者表达的交集的时候 - 127 到 -126 是一道坎，如果把它两的表达范围画个图的话，就会出现一个断层，大概就是下图黑线所示(此处图片只为形象解释)

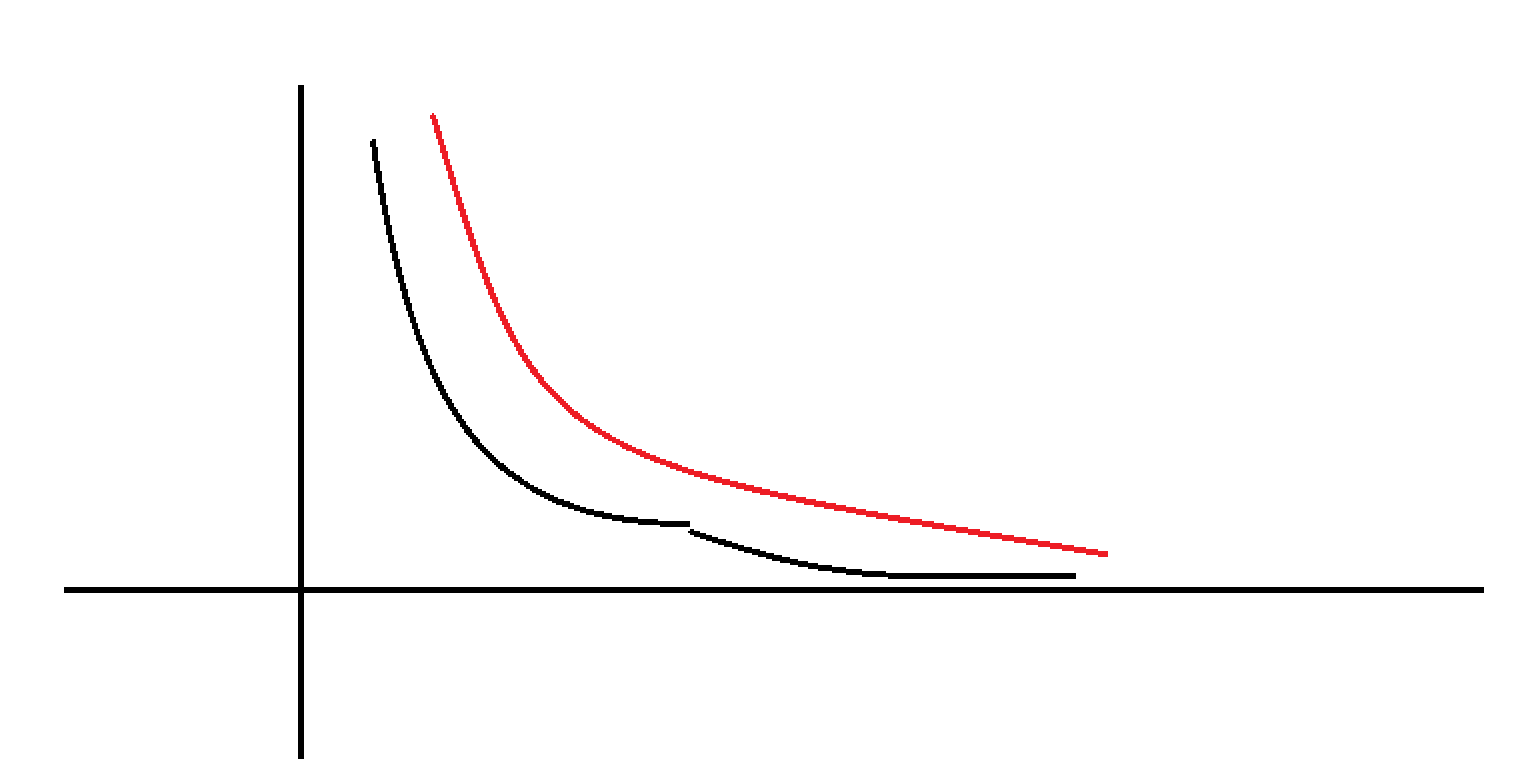
红线则可以视为对非规格化数的偏置加上1的平滑表示

由此我们基本可以了解规格化数和非规格化数的含义及区别

此外IEEE还规定了几个特殊的值

注：此类值只针对阶码全为1的值

正无穷：尾数全为0，且符号位为0；

负无穷：尾数全为0，且符号位为1；

NaN：当尾数值不全为0，"not a number" 即不是一个数 如：计算就会返回NaN.

以上就是对IEEE规定的浮点数标准进行的总结，我们试着类比于使用规则1的方式，使用IEEE标准实现十进制小数和二进制之间的相互转化。(下面实例都为32位单精度下的转化)

重点：考试就考下面的转化

例：-10.25

整数部分：10 —— 对应二进制 1010

小数部分：0.25——对应二进制 .01

符号部分：-1 —— 对应符号位 1

得到二进制串：1010.01

使用科学计数法表达：

  //到这一步为止，其与我们自定的规则计算的都是一样的

得到 E = 3，由 E = e - bais 我们得到阶码段的数位 e = bais + E = 127 + 3 = 130

所以 e 对应的二进制阶码段为：1000 0010

尾数段W对应的二进制串为：01001 (注意，由于不是趋近于0，所以使用的是规格化数隐去1规则)

所以填充进32位串里得到：

小tips:

        当我们转化的十进制过小时，我们会发现规格化处理不了它，那么就要使用非规格化处理它 

 

同样二进制转十进制

 例：1 | 1000 0000 | 1100...00

//注意这里转换尾数时，我们必须要知道这个串是按照规格化解读还是非规格化解读，这关乎到小数点前面是否读出1，这里看阶码段是不是全为0，全为0就是非规格数，这里显然是规格化数//

得到 S = 1，e = 128，M = 1.11（e为十进制形式）

而 E = e - basi = 128 - 127 = 1

由十进制下的科学计数法转化得到二进制串 11.1

整数部分 11 —— 对应十进制3

小数部分 .1——对应十进制0.5

符号部分 1 ——对应符号 -

所以得到十进制下的该数 -3.5

至此浮点数的基本内容就基本讲解完毕了，文中很多描述都带有作者自己的主观想法，且证明方式都是伪证明，并没有给出具体原理，所以肯定存在些纰漏和不足，望理解。