离散数学实验三c语言(判断运算的性质：封闭性、可结合性、可交换性、幺元、零元、逆元、计算元素的阶、判断是否为特殊的代数系统)

原创于 2024-10-16 09:16:49 发布 · 1k 阅读

14 ·

CC 4.0 BY-SA版权

文章标签：

#c语言 #开发语言 #离散数学 #大作业 #课程设计

课程设计大作业专栏收录该内容

6 篇文章

订阅专栏

离散数学实验三

一、算法描述、算法思想

（一）相关数据结构

typedef struct Set *S;
typedef struct Set Set; //存集合
struct Set
{
    char *str;                           //集合s元素
    char *ni;                            //集合s元素的逆元
    char yao, ling;                      //集合s的幺元
    int *YJ;                             //元素阶
    int size, f, jie, jiao, isni, isxun; //集合s的元素个数，是否封闭，是否结合，是否交换，是否每个元素都有逆元，都有阶
};

Set结构用来存储集合元素及其性质等，str存储集合元素，ni存储每个元素的逆元，yao存储集合的幺元，ling存储集合的零元，YJ存储每个元素的阶，size存储集合元素个数，f为1表示该代数系统具有封闭性、jie为1表示该代数系统具有结合性、jiao为1表示该代数系统具有交换性、isni为1表示该集合的所有元素均具有逆元、isxun为1表示该代数系统的每个元素均具有阶。

yao,ling默认值为'0', ni每个默认值具为‘0’，f, jie, jiao, isni, isxun默认值均为0。YJ每个元素默认值也为0。

typedef struct Operator *O;
typedef struct Operator Operator; //存运算结果
struct Operator
{
    char **str; //集合s每个元素运算结果
    int size;   //集合s元素个数
};

Operator存储该集合所有运算的结果，str二维字符数组存储运算结果，如第0行第0列表示集合第一个元素与第一个元素运算结果，0行1列，表示集合第一个元素与第二个元素运算结果，size存储该集合元素大小，即运算结果矩阵横纵坐标的范围。

（二）相关算法实现

1、判断运算的性质

（1）判断是否具有封闭性

    //封闭
    for (int i = 0; i < size; i++)
    {
        for (int j = 0; j < size; j++)
        {
            char res = o->str[i][j];
            if (findS(s, res) == -1)
            {
                panf = 1;
                break;
            }
        }
    }
    if (!panf)
    {
        s->f = 1;
        printf("该运算具有封闭性\n");
    }

从集合取出任意两个元素，看其运算结果是否还在集合内，若有一个结果不在集合内，就说明其不具有封闭性，反之，若所有结果均在集合内则该运算具有封闭性。

（2）判断是否具有可结合性

    //结合
    for (int i = 0; i < s->size; i++)
    {
        for (int j = 0; j < s->size; j++)
        {
            for (int k = 0; k < s->size; k++)
            {
                char ch1 = oper(s, o, s->str[i], s->str[j]);
                char ch2 = oper(s, o, s->str[j], s->str[k]);
                if (findS(s, ch1) != -1 && findS(s, ch2) != -1)
                {
                    char res1 = oper(s, o, ch1, s->str[k]);
                    char res2 = oper(s, o, s->str[i], ch2);
                    // printf("(%c*%c)*%c = %c \n", s->str[i], s->str[j], s->str[k], res1);
                    // printf("%c*(%c*%c) = %c \n", s->str[i], s->str[j], s->str[k], res2);
                    if (res1 != res2)
                    {
                        panj = 1;
                        break;
                    }
                }
                else
                {
                    panj = 1;
                    break;
                }
            }
        }
    }
    if (!panj)
    {
        s->jie = 1;
        printf("该运算具有可结合性\n");
    }

从集合中任意取出三个元素a,b,c，计算abc == a(bc) ，若找到一组不满该条件，则该运算不具有结合性，反之，若所有可能都满足该条件，则该运算满足可结合性。

（3）判断是否具有可交换性

    //交换
    for (int i = 0; i < s->size; i++)
    {
        for (int j = 0; j < s->size; j++)
        {
            char res1 = oper(s, o, s->str[i], s->str[j]);
            char res2 = oper(s, o, s->str[j], s->str[i]);
            if (res1 != res2)
            {
                panji = 1;
                break;
            }
        }
    }
    if (!panji)
    {
        s->jiao = 1;
        printf("该运算具有可交换性\n");
    }

从集合取出任意两个元素a,b,若ab == ba，且所有的可能均满足条件则说明该运算具有可交换性，反之，若有一组不满足条件，则该运算不具有可交换性。

（4）判断并计算集合幺元

    //幺元
    for (int i = 0; i < s->size; i++) //枚举幺元
    {
        pany = 0;
        for (int j = 0; j < s->size; j++)
        {
            char res1 = oper(s, o, s->str[i], s->str[j]);
            char res2 = oper(s, o, s->str[j], s->str[i]);
            if (res1 == res2 && res1 == s->str[j])
                continue;
            pany = 1;
            break;
        }
        if (!pany)
        {
            yao = s->str[i];
            break;
        }
    }
    if (!pany)
    {
        s->yao = yao;
        printf("运算具有幺元：%c\n", yao);
    }

枚举集合中的每一个元素，看其是否满足幺元性质，若有一个元素和其他所有元素的运算，ab且ba等于b,则说明a为幺元。

（5）判断并计算集合零元

    //零元
    for (int i = 0; i < s->size; i++) //枚举零元
    {
        panl = 0;
        for (int j = 0; j < s->size; j++)
        {
            char res1 = oper(s, o, s->str[i], s->str[j]);
            char res2 = oper(s, o, s->str[j], s->str[i]);
            if (res1 == res2 && res1 == s->str[i])
                continue;
            panl = 1;
            break;
        }
        if (!panl)
        {
            ling = s->str[i];
            break;
        }
    }
    if (!panl)
    {
        s->ling = ling;
        printf("运算具有零元：%c\n", ling);
    }

枚举集合中的每一个元素，看其是否满足幺元性质，若有一个元素和其他所有元素的运算，ab且ba等于a,则说明a为零元。

（6）判断并计算集合元素逆元

    //逆元
    if (yao != '0') //有幺元
    {
        for (int i = 0; i < s->size; i++)
        {
            for (int j = 0; j < s->size; j++) //找i的逆元
            {
                char res1 = oper(s, o, s->str[i], s->str[j]);
                char res2 = oper(s, o, s->str[j], s->str[i]);
                if (res1 == yao && res2 == yao)
                {
                    s->ni[i] = s->str[j];
                    break;
                }
            }
        }
        printf("该运算具有逆元：\n");
        for (int i = 0; i < s->size; i++)
        {
            if (s->ni[i] != '0')
                printf("%c的逆元为: %c\n", s->str[i], s->ni[i]);
            else
                panni = 1;
        }
        if (!panni)
            s->isni = 1;
    }

首先在该集合存在幺元的情况下，找每一元素的逆元，若元素a,b,有ab == 幺元， ba == 幺元，则a,b互为逆元。

2、计算元素的阶

首先要在集合有幺元，且封闭的条件下来计算。

int CalcJie(S s, O o, char ch)
{
    int pos1 = findS(s, ch), pos2 = findS(s, ch);
    int vis[1000] = {0};
    vis[ch - 'a'] = 1;
    int cnt = 1;
    if (ch == s->yao)
        return 1;
    while (!vis[o->str[pos1][pos2] - 'a'])
    {
        cnt++;
        if (o->str[pos1][pos2] == s->yao)
        return cnt;
        vis[o->str[pos1][pos2] - 'a'] = 1;
        pos1 = findS(s, o->str[pos1][pos2]);
    }
    return 0;
}

计算集合元素ch的阶，若元素ch为幺元，则阶为1。若元素ch不为幺元，先标记ch访问过，然后计算ch与ch的运算结果，若结果为幺元，则阶为2，若不为幺元，则标记该运算结果访问过，然后将该运算结果与ch做运算，直到结果访问过或者结果为幺元为止。若最后是因为结果为幺元而退出，则返回cnt，cnt即为该元素ch的阶。若是因为再次得到同一结果而退出，则说明该元素ch没有阶。

3、判断是否为特殊的代数系统

void PanSetCharacter(S s)
{
    if (s->f == 1 && s->jie == 1 && s->yao != '0' && s->isni == 1 && s->jiao == 1 && s->isxun == 1)
        printf("该代数系统为循环群\n");

    else if (s->f == 1 && s->jie == 1 && s->yao != '0' && s->isni == 1 && s->jiao == 1)
        printf("该代数系统为交换群\n");

    else if (s->f == 1 && s->jie == 1 && s->yao != '0' && s->isni == 1)
        printf("该代数系统为群\n");

    else if (s->f == 1 && s->jie == 1 && s->yao != '0')
        printf("该代数系统为独异点\n");

    else if (s->f == 1 && s->jie == 1)
        printf("该代数系统为半群\n");
}

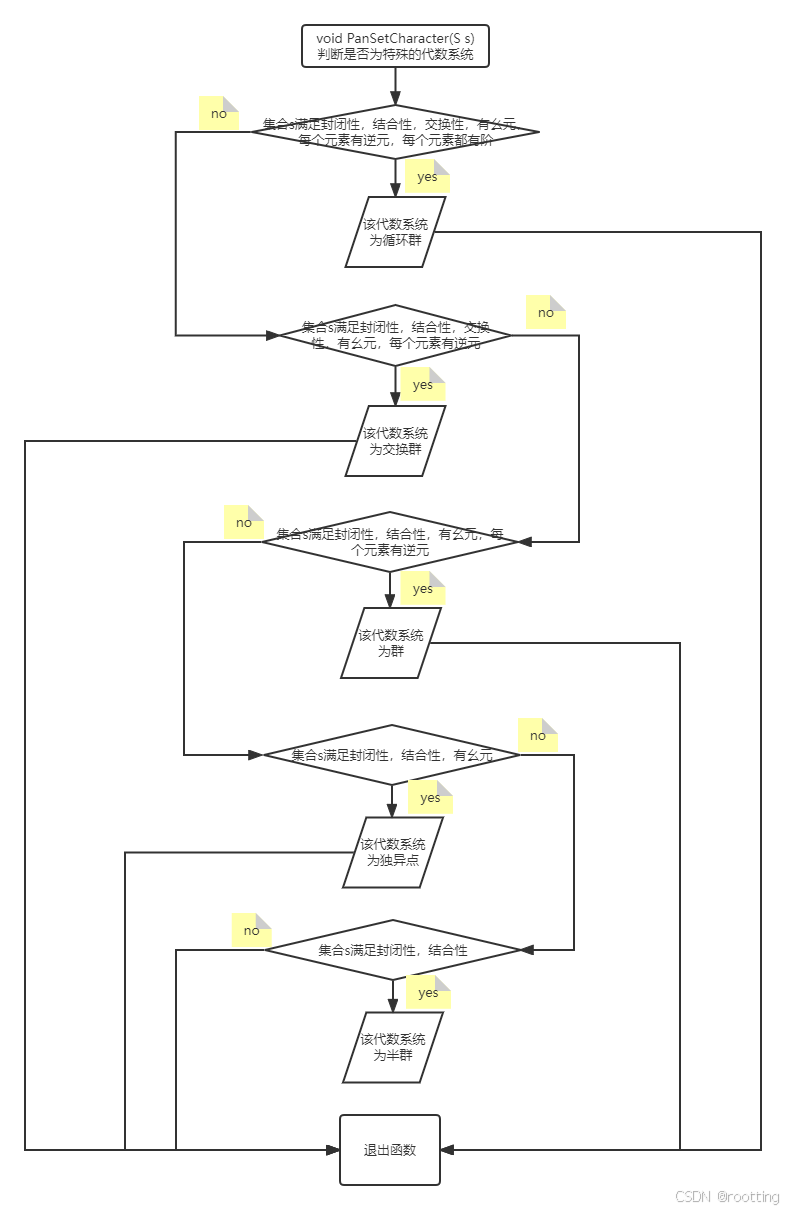
（1）集合s满足封闭性，结合性，交换性，有幺元，每个元素有逆元，每个元素都有阶，则该代数系统为循环群

（2）集合s满足封闭性，结合性，交换性，有幺元，每个元素有逆元，则该代数系统为交换群。

（3）集合s满足封闭性，结合性，有幺元，每个元素有逆元，则该代数系统为群。

（4）集合s满足封闭性，结合性，有幺元，则该代数系统为独异点。

（5）集合s满足封闭性，结合性，则该代数系统为半群。

（6）若以上条件没一个满足，说明不为特殊的代数系统。

（三）流程图

（1）main主函数

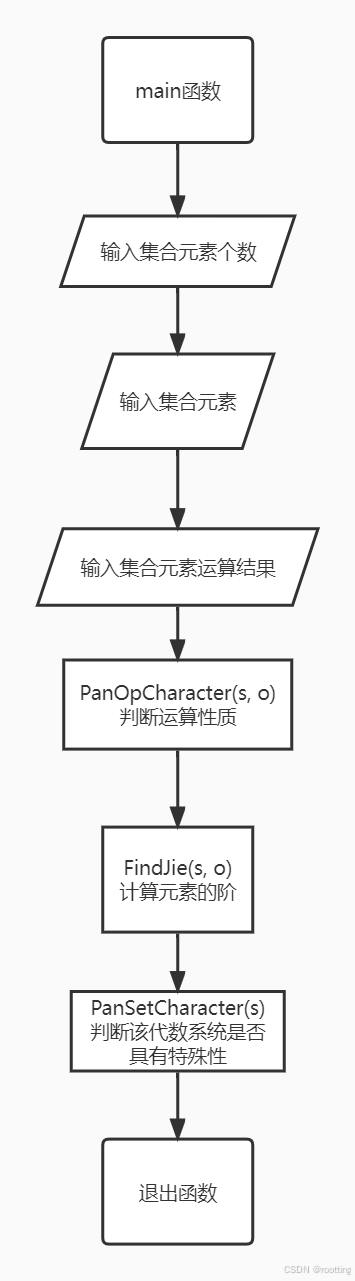
（2）判断运算的性质

（3）计算元素的阶

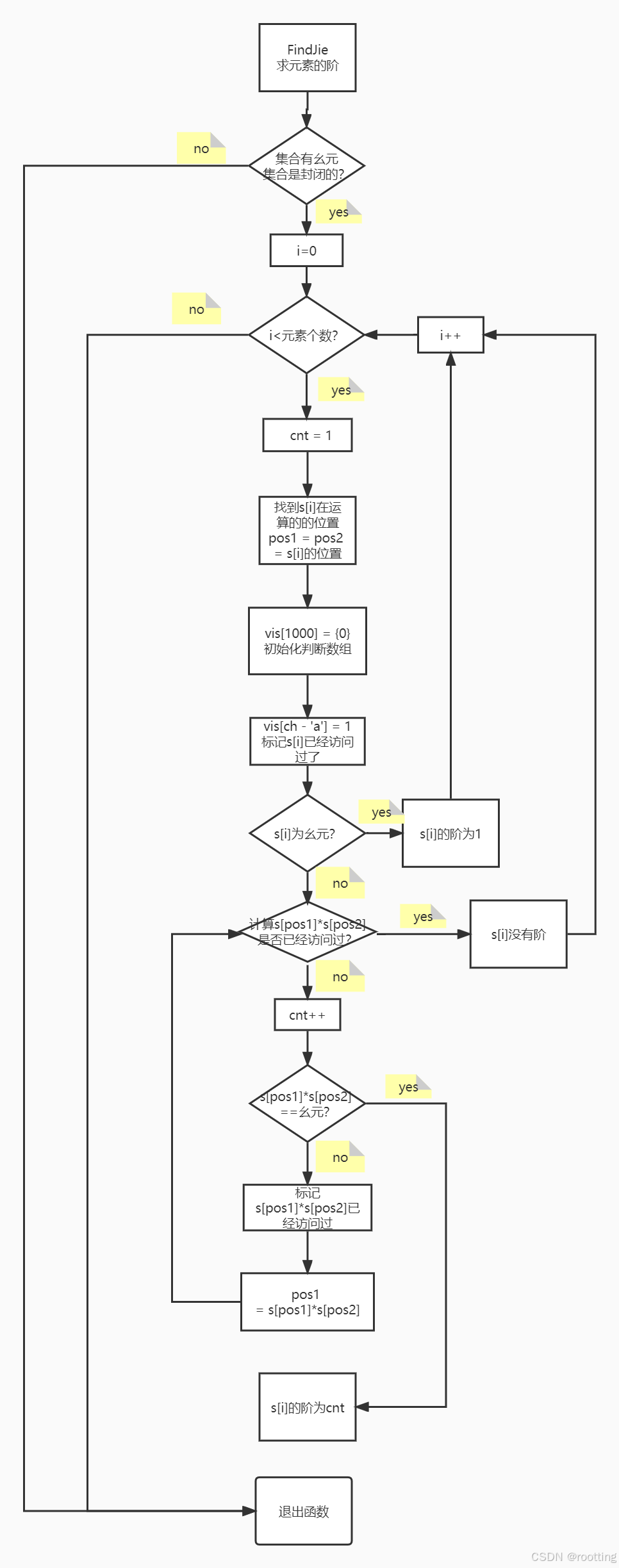
（4）判断是否为特殊的代数系统

二、程序运行截图，即相关样例解释

以下样例中集合元素均为a,b,c。

（一）验证封闭性判断

以下为两个代数系统，及其分析

程序运行结果

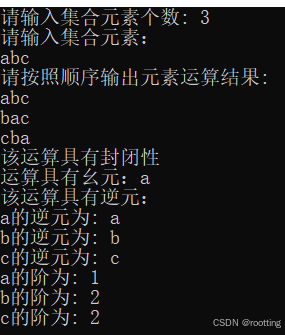
（二）验证可结合性判断

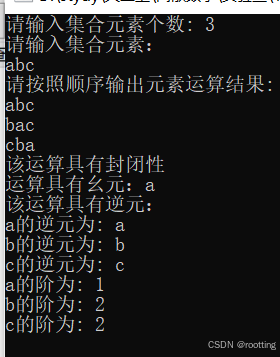
（三）验证逆元计算

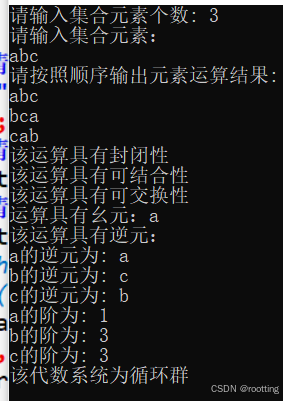
（四）验证可交换性判断

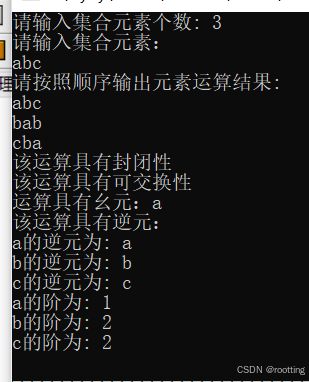
（五）验证元素阶计算

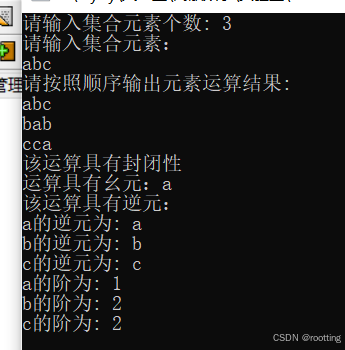
其余幺元，代数系统的特殊性判断，在例子里也有说明。

三、源程序

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct Set *S;
typedef struct Set Set; //存集合
struct Set
{
    char *str;                           //集合s元素
    char *ni;                            //集合s元素的逆元
    char yao, ling;                      //集合s的幺元
    int *YJ;                             //元素阶
    int size, f, jie, jiao, isni, isxun; //集合s的元素个数，是否封闭，是否结合，是否交换，是否每个元素都有逆元，都有阶
};
typedef struct Operator *O;
typedef struct Operator Operator; //存运算结果
struct Operator
{
    char **str; //集合s每个元素运算结果
    int size;   //集合s元素个数
};
S InitSet(int size) //初始化集合s
{
    S s = (S)malloc(sizeof(Set));
    s->size = size;
    s->str = (char *)malloc(sizeof(char) * size);
    s->ni = (char *)malloc(sizeof(char) * size);
    s->jiao = 0, s->jie = 0, s->f = 0, s->isni = 0, s->isxun = 0;
    s->YJ = (int *)malloc(sizeof(int) * size);
    s->yao = '0', s->ling = '0';
    char ch;

    for (int i = 0; i < size; i++)
    {
        scanf("%c", &ch);
        s->str[i] = ch;
        s->ni[i] = '0';
        // printf("%c", ch);
    }
    getchar();
    return s;
}
O InitOperator(int size) //初始化集合o
{
    O o = (O)malloc(sizeof(Operator));
    o->size = size;
    o->str = (char **)malloc(sizeof(char *) * size);
    for (int i = 0; i < size; i++)
    {
        o->str[i] = (char *)malloc(sizeof(char) * size);
        for (int j = 0; j < size; j++)
            scanf("%c", &o->str[i][j]);
        getchar();
    }
    // getchar();
    return o;
}
void PrintSet(S s) //输出集合s的元素，调试代码用
{
    for (int i = 0; i < s->size; i++)
        printf("%c ", s->str[i]);
    printf("\n");
}
void PrintOperator(O o) //输出运算结果，调试代码用
{
    for (int i = 0; i < o->size; i++)
    {
        for (int j = 0; j < o->size; j++)
            printf("%c ", o->str[i][j]);
        printf("\n");
    }
    printf("\n");
}
void FreeSet(S s) //释放集合s内存
{
    free(s->str);
    free(s->ni);
    free(s->YJ);
    free(s);
}
void FreeOperator(O o) //释放o内存
{
    for (int i = 0; i < o->size; i++)
        free(o->str[i]);
    free(o->str);
    free(o);
}

int findS(S s, char ch) //找元素ch在s中的位置
{
    int size = s->size;
    for (int i = 0; i < size; i++)
    {
        if (s->str[i] == ch)
            return i;
    }
    return -1; //元素ch不在集合s中
}
char oper(S s, O o, char ch1, char ch2) // ch1*ch2
{
    int pos1 = findS(s, ch1);
    int pos2 = findS(s, ch2);
    return o->str[pos1][pos2];
}

void PanOpCharacter(S s, O o) //判断运算的性质
{
    int panf = 0, panj = 0, panji = 0, pany = 0, panl = 0, panni = 0;
    char yao = '0', ling = '0';
    int size = s->size;
    //封闭
    for (int i = 0; i < size; i++)
    {
        for (int j = 0; j < size; j++)
        {
            char res = o->str[i][j];
            if (findS(s, res) == -1)
            {
                panf = 1;
                break;
            }
        }
    }
    if (!panf)
    {
        s->f = 1;
        printf("该运算具有封闭性\n");
    }

    //结合
    for (int i = 0; i < s->size; i++)
    {
        for (int j = 0; j < s->size; j++)
        {
            for (int k = 0; k < s->size; k++)
            {
                char ch1 = oper(s, o, s->str[i], s->str[j]);
                char ch2 = oper(s, o, s->str[j], s->str[k]);
                if (findS(s, ch1) != -1 && findS(s, ch2) != -1)
                {
                    char res1 = oper(s, o, ch1, s->str[k]);
                    char res2 = oper(s, o, s->str[i], ch2);
                    // printf("(%c*%c)*%c = %c \n", s->str[i], s->str[j], s->str[k], res1);
                    // printf("%c*(%c*%c) = %c \n", s->str[i], s->str[j], s->str[k], res2);
                    if (res1 != res2)
                    {
                        panj = 1;
                        break;
                    }
                }
                else
                {
                    panj = 1;
                    break;
                }
            }
        }
    }
    if (!panj)
    {
        s->jie = 1;
        printf("该运算具有可结合性\n");
    }

    //交换
    for (int i = 0; i < s->size; i++)
    {
        for (int j = 0; j < s->size; j++)
        {
            char res1 = oper(s, o, s->str[i], s->str[j]);
            char res2 = oper(s, o, s->str[j], s->str[i]);
            if (res1 != res2)
            {
                panji = 1;
                break;
            }
        }
    }
    if (!panji)
    {
        s->jiao = 1;
        printf("该运算具有可交换性\n");
    }

    //幺元
    for (int i = 0; i < s->size; i++) //枚举幺元
    {
        pany = 0;
        for (int j = 0; j < s->size; j++)
        {
            char res1 = oper(s, o, s->str[i], s->str[j]);
            char res2 = oper(s, o, s->str[j], s->str[i]);
            if (res1 == res2 && res1 == s->str[j])
                continue;
            pany = 1;
            break;
        }
        if (!pany)
        {
            yao = s->str[i];
            break;
        }
    }
    if (!pany)
    {
        s->yao = yao;
        printf("运算具有幺元：%c\n", yao);
    }

    //零元
    for (int i = 0; i < s->size; i++) //枚举零元
    {
        panl = 0;
        for (int j = 0; j < s->size; j++)
        {
            char res1 = oper(s, o, s->str[i], s->str[j]);
            char res2 = oper(s, o, s->str[j], s->str[i]);
            if (res1 == res2 && res1 == s->str[i])
                continue;
            panl = 1;
            break;
        }
        if (!panl)
        {
            ling = s->str[i];
            break;
        }
    }
    if (!panl)
    {
        s->ling = ling;
        printf("运算具有零元：%c\n", ling);
    }

    //逆元
    if (yao != '0') //有幺元
    {
        for (int i = 0; i < s->size; i++)
        {
            for (int j = 0; j < s->size; j++) //找i的逆元
            {
                char res1 = oper(s, o, s->str[i], s->str[j]);
                char res2 = oper(s, o, s->str[j], s->str[i]);
                if (res1 == yao && res2 == yao)
                {
                    s->ni[i] = s->str[j];
                    break;
                }
            }
        }
        printf("该运算具有逆元：\n");
        for (int i = 0; i < s->size; i++)
        {
            if (s->ni[i] != '0')
                printf("%c的逆元为: %c\n", s->str[i], s->ni[i]);
            else
                panni = 1;
        }
        if (!panni)
            s->isni = 1;
    }
}
int CalcJie(S s, O o, char ch) //计算ch的阶
{
    int pos1 = findS(s, ch), pos2 = findS(s, ch);
    int vis[1000] = {0};
    vis[ch - 'a'] = 1;
    int cnt = 1;
    if (ch == s->yao)
        return 1;
    while (!vis[o->str[pos1][pos2] - 'a']) //若结果已经访问过了
    {
        cnt++;
        if (o->str[pos1][pos2] == s->yao) //若结果为幺元
            return cnt;
        vis[o->str[pos1][pos2] - 'a'] = 1;
        pos1 = findS(s, o->str[pos1][pos2]);
    }
    return 0;
}
void FindJie(S s, O o) //计算元素的阶
{
    int jie = 0, panxun = 0;
    if (s->yao != '0' && s->f == 1)
    {
        for (int i = 0; i < s->size; i++)
        {
            jie = CalcJie(s, o, s->str[i]);
            if (jie) //若该元素有阶
                printf("%c的阶为: %d\n", s->str[i], jie);
            else
                panxun = 1;
        }
    }
    if (!panxun)
        s->isxun = 1;
}
void PanSetCharacter(S s) //判断是否为特殊的代数系统
{
    if (s->f == 1 && s->jie == 1 && s->yao != '0' && s->isni == 1 && s->jiao == 1 && s->isxun == 1)
        printf("该代数系统为循环群\n");

    else if (s->f == 1 && s->jie == 1 && s->yao != '0' && s->isni == 1 && s->jiao == 1)
        printf("该代数系统为交换群\n");

    else if (s->f == 1 && s->jie == 1 && s->yao != '0' && s->isni == 1)
        printf("该代数系统为群\n");

    else if (s->f == 1 && s->jie == 1 && s->yao != '0')
        printf("该代数系统为独异点\n");

    else if (s->f == 1 && s->jie == 1)
        printf("该代数系统为半群\n");
}

int main()
{
    int n;
    printf("请输入集合元素个数: ");
    scanf("%d", &n);
    getchar();

    printf("请输入集合元素：\n");
    S s = InitSet(n);
    printf("请按照顺序输出元素运算结果:\n");
    O o = InitOperator(n);

    PanOpCharacter(s, o); //输出运算性质
    FindJie(s, o);        //输出元素的阶
    PanSetCharacter(s);   //判断是否为特殊的代数系统

    FreeSet(s);
    FreeOperator(o);
    return 0;
}