离散数学实验一c语言(数理逻辑，输入命题公式，输出真值表，主析取范式，主合取范式，给出命题公式类别)

最新推荐文章于 2025-02-14 23:22:06 发布

rootting

最新推荐文章于 2025-02-14 23:22:06 发布

阅读量2.3k

点赞数 20

分类专栏：课程设计大作业文章标签：算法离散数学大作业实验

本文链接：https://blog.csdn.net/m0_60531106/article/details/142912832

版权

课程设计大作业专栏收录该内容

6 篇文章

订阅专栏

一、算法描述、算法思想：

(一)符号表示：

命题变元：字母（区分大小写，即大写和小写字母是不同的变元）

操作连接词：0--合取、1--析取、2--条件、3--双条件

否定：’（A’表示A变元的否定）

(二)数据结构

typedef struct Stack *S; //栈用来存储命题公式中的逻辑连结词，命题变元
struct Stack
{
    char *ch;
    int top;
};

该栈是用来计算命题公式的真值。

typedef struct SqlList *L; //线性表用来存储相同的变元的不同位置，其命题和命题的否定是分开存储的
struct SqlList
{
    char ch;
    int *elem;            //存该命题变元的位置
    int lengthe; // lengthe为该命题变元的总数
};

该线性表是用来存储命题公式中相同的变元的全部位置。

char ChangeStr[100][100];                     //存储所有可能的命题变元取真假后的命题公式
char XiStr[100][100];                         //存储主析取范式的命题公式
char HeStr[100][100];                         //存储主合取范式的命题公式
char targetch[100];                           //存储该命题公式所有不同的变元
int pos[100];                                 //映射作用，其下标对应变元的序号，值对应该变元第一次出现的位置
int total, totalXi, totalHe, cnt, panz, panj; // total为所有可能的命题变元取真假后的命题公式的个数，即ChangeStr的个数
// totalXi为主析取范式的个数，totalHe为主合取范式的个数，cnt为总共不同变元的个数，panz和panj为判断该命题公式类型的变量

其次，还有以上变量

(三)主要功能实现：

输出真值表：

处理原命题公式

L ProcessStr(char str[]) //处理原命题公式，计算所有可能的真值指派

首先将原命题公式所有的命题变元改为真值F，方便计算指派变元真值后，该命题公式的真值。

用线性表数组，cnt为不同命题变元的序号，l[cnt]则存储第cnt个变元的所有位置，方便后序指派真值。

进行真值指派：

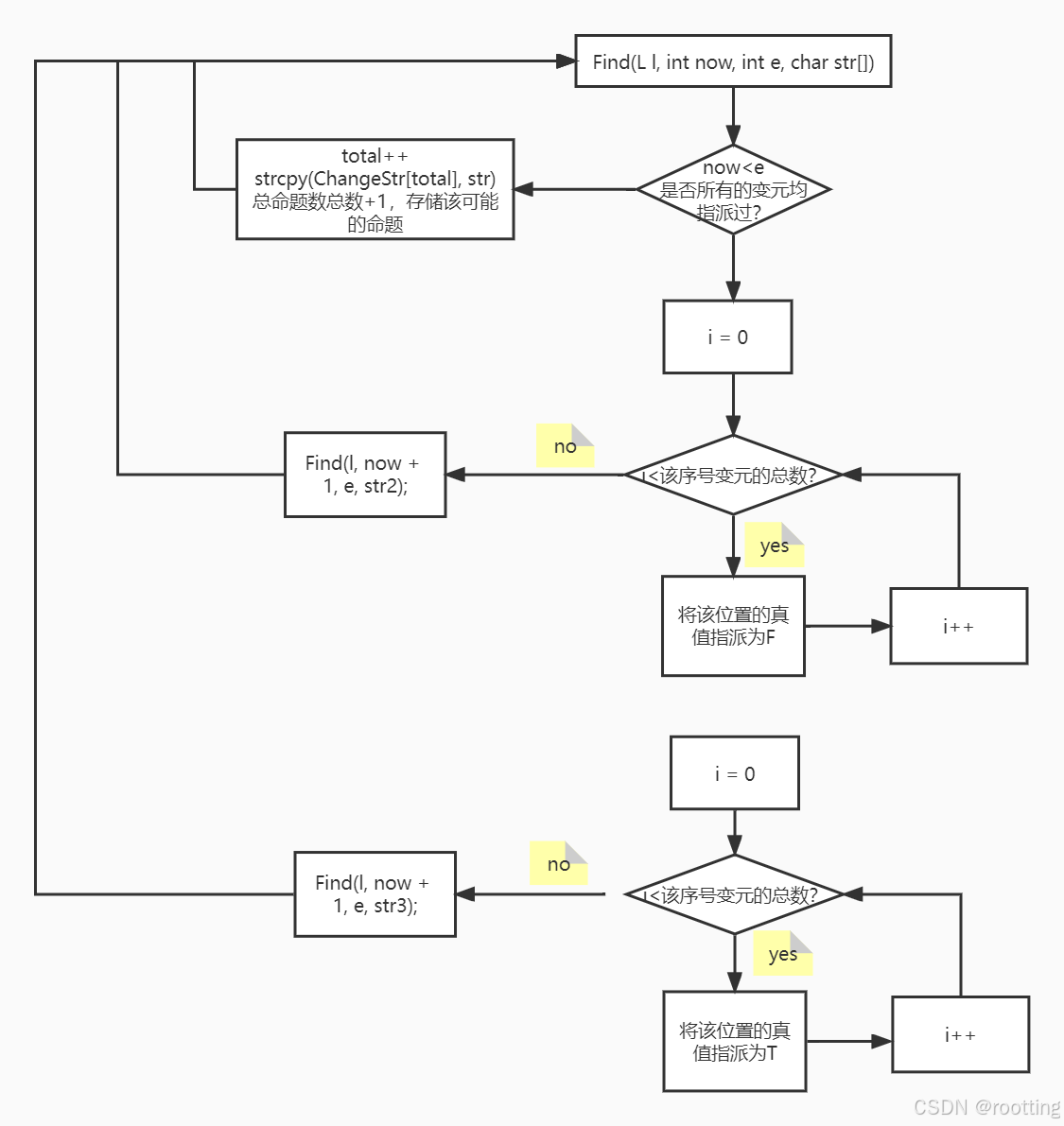
void Find(L l, int now, int e, char str[]) //将str里的所有命题变元进行真值指派，now指当前到第几个变元，e为总共的变元数

利用递归思想，分析str中所有的命题变元均有两个取值，即F、T，那么我们就递归的将每一个变元进行真值指派，即先令第一个变元为F，然后第二个变元为F......照这样将所有命题变元指派完后，存储该可能的命题公式的指派，然后回退return，即回到上一层将最后一个变元真值改为T，然后再记录，再回退，以此类推。

该str为处理后的命题公式，即所有的变元均为F，now为当前正在处理第cnt个变元，e指总共不同的变元个数。l线性表即存放着每个命题变元的位置。

计算命题公式的真值：

char Calculate(char str[]) //计算str公式的真值

利用栈的思想，将操作连接符存到一个栈里，将变元存到另一个栈里。首先匹配命题公式，遇到操作符，根据操作符等级，如果为左括号或者操作符栈为空，则一定入操作符栈，遇到当前操作符的优先级>=操作符栈栈顶优先级，则也一定入栈，小于等于则先取出操作符栈和变元栈顶元素计算，然后再次判断，直到符合要求为止。遇到变元也将其入栈，一但遇到右括号，那么就要再次出栈计算，计算后再将其入栈，直到遇到左括号为止，最后匹配完公式，还得继续计算剩下的操作符和变元。

char Pan(char op, char le1, char le2) //对变元le1,变元le2进行逻辑连接词判断真假
char Pan2(char op, char le1)//计算变元否定的操作

计算变元经过操作连结词后的真值。Pan是对二元操作符如析取、合取等的计算，Pan2是一元操作符如取否定的计算。

输出真值表：

L InputTrueTable(char str[])

将计算后的真值和公式，对应输出其对应的命题变元的真值，和该命题公式真值。

判断命题公式类型：

char res = Calculate(ChangeStr[i]); //计算该命题公式的真值
        if (res == 'T')
        {
            strcpy(XiStr[totalXi++], ChangeStr[i]);
            panj = 0; //则该命题公式不可能为一个永假式
        }
        else
        {
            strcpy(HeStr[totalHe++], ChangeStr[i]);
            panz = 0; //该命题公式不可能为一个用真式
        }

在输出真值表的同时，判断下是否该命题公式中的变元经过指派后，该公式的真值一直为真，或者假，然后输出即可。

输出主析取范式、主合取范式：

void FindZhu(int cnt, L l) //输出主析取范式、主合取范式

在输出真值表的同时，也将那些真值为T的命题存下，真值为F的存下，然后在根据变元位置，重新组成命题公式后输出，主析取范式，即取命题最后为T的，如果变元为T则取原变元，为F取该变元的否定，并永合取将其连结这就是一个合取式，最后再将合取式析取为主析取范式。主合取范式类似，即找到真值为F的析取式，将其合取起来。

二、流程图：

Main

InputTrueTable(输出真值表)

ProcessStr(处理原命题公式，使其更方便计算)

Find(列出所有真值指派的命题公式)

Calculate(计算命题公式的真值)

Devide(判断命题公式的类型)

FindZhu(输出主析取范式，主合取范式)

ChangeStr(处理主析取范式中的合取式、主合取范式的析取式)

运行截图：

由图可看出，对于命题公式：P→(Q∧R)∧(┐p→(┐Q∧┐R))

该命题公式包含了优先级、括号、非、合取、条件等运算，大概率可以检测程序的可靠性

说明：

先是输出该命题公式的真值表、命题公式类型

根据真值输出主析取范式、主合取范式

源代码：

#include <stdio.h>
#include <stdlib.h>
#include <string.h>
typedef struct Stack *S; //栈用来存储命题公式中的逻辑连结词，命题变元
struct Stack
{
    char *ch;
    int top;
};
typedef struct SqlList *L; //线性表用来存储相同的变元的不同位置，其命题和命题的否定是分开存储的
struct SqlList
{
    char ch;
    int *elem;            //存该命题变元的位置
    int lengthe; // lengthe为该命题变元的总数
};
char ChangeStr[100][100];                     //存储所有可能的命题变元取真假后的命题公式
char XiStr[100][100];                         //存储主析取范式的命题公式
char HeStr[100][100];                         //存储主合取范式的命题公式
char targetch[100];                           //存储该命题公式所有不同的变元
int pos[100];                                 //映射作用，其下标对应变元的序号，值对应该变元第一次出现的位置
int total, totalXi, totalHe, cnt, panz, panj; // total为所有可能的命题变元取真假后的命题公式的个数，即ChangeStr的个数
// totalXi为主析取范式的个数，totalHe为主合取范式的个数，cnt为总共不同变元的个数，panz和panj为判断该命题公式类型的变量
int prior[10] = {1, 1, 0, 0, 2};
char p[10] = {'0', '1', '2', '3', '\''};
//对栈的操作
S InitStack(int size) //初始化栈
{
    S s = (S)malloc(sizeof(struct Stack));
    s->ch = (char *)malloc(sizeof(char) * size);
    s->top = 0;
}
int EmptyStack(S s) //判断栈是否为空，空则返回1，否则返回0
{
    if (s->top == 0)
        return 1;
    else
        return 0;
}
void PushStack(S s, char c) //将c入栈
{
    s->ch[s->top++] = c;
}
char StackTop(S s)//返回栈顶元素，不出栈
{
    return s->ch[s->top-1];
}
char PopStack(S s) //返回栈顶元素，并出栈
{
    return s->ch[--s->top];
}
void freeStack(S s) //释放栈的内存
{
    free(s->ch);
    free(s);
}
void PrintStack(S s)//用来调试程序
{
    int total = 1;
    while (total<=s->top)
    {
        printf("%c ", s->ch[s->top-total]);
        total++;
    }
    printf("\n");
}

//对线性表的操作
L InitList(int size) //初始化线性表，返回线性表数组
{
    L l = (L)malloc(sizeof(struct SqlList) * (size + 1));
    for (int i = 0; i <= size; i++)
    {
        l[i].ch = '\0';
        l[i].elem = (int *)malloc(sizeof(int) * size);
        l[i].lengthe = 0;
    }
    return l;
}
void freeList(L l) //释放该线性表内存
{
    free(l->elem);
    free(l);
}

//对命题公式的操作
char Pan(char op, char le1, char le2) //对变元le1,变元le2进行逻辑连接词判断真假
{
    if (op == '1') //析取
    {
        if (le1 == 'T' || le2 == 'T')
            return 'T';
        else
            return 'F';
    }
    else if (op == '0') //合取
    {
        if (le1 == 'T' && le2 == 'T')
            return 'T';
        else
            return 'F';
    }
    else if (op == '2') //条件
    {
        if (le1 == 'T' && le2 == 'F')
            return 'F';
        else
            return 'T';
    }
    else if (op == '3') //非条件
    {
        if (le1 == le2)
            return 'T';
        else
            return 'F';
    }
}
char Pan2(char op, char le1)//计算变元否定的操作
{
    if (op == '\'')
    {
        if (le1 == 'F')
        return 'T';
        else
        return 'F';
    }
}
char Cal(S s1, S s2)//s1符号、s2字母
{
    char op = PopStack(s1), le1, le2;
    if (op == '\'')
    {
        char le1 = PopStack(s2);
        return Pan2(op, le1);
    }
    else
    {
        char le2 = PopStack(s2);
        char le1 = PopStack(s2);
        return Pan(op, le1, le2);
    }
}
int panLevel(char ch)
{
    if (ch == '\'')
    return prior[4];
    else if (ch == '(')
    return -100;
    else
    return prior[ch-'0'];
}
char Calculate(char str[]) //计算str公式的真值
{
    char le1, le2, op, res;
    int len = strlen(str);
    S s1 = InitStack(len); //符号栈（1、0）
    S s2 = InitStack(len); //字母栈 (T、F)
    int i = 0;
    while (i < len)
    {
        if (str[i] == '1' || str[i] == '0' || str[i] == '(' || str[i] == '2' || str[i] == '3' || str[i] == '\'') //若当前字符为操作符号
        {
            if (str[i] == '('||EmptyStack(s1))
            {
                PushStack(s1, str[i]); //入操作符栈
                i++;
                continue;
            }
            int level = panLevel(str[i]);
            int level2 = panLevel(StackTop(s1));
            if (level >= level2)
            PushStack(s1, str[i]); //入操作符栈
            else
            {
                while (1)
                {
                    res = Cal(s1, s2);
                    PushStack(s2, res);
                    level = panLevel(str[i]);
                    level2 = panLevel(StackTop(s1));
                    if (level>=level2)
                    {
                        PushStack(s1, str[i]);
                        break;
                    }
                }
            }
        }
        else if (str[i] == ')') //若为右括号，则将操作符里的连结词出栈，计算，直到操作符栈中处理到左括号为止
        {
            while (1)
            {
                op = StackTop(s1);
                if (op == '(')
                {
                    PopStack(s1);
                    break;
                }
                res = Cal(s1, s2);
                PushStack(s2, res);
            }
        }
        else
        PushStack(s2, str[i]);
        i++;
        
    }
    while (!EmptyStack(s1) && !EmptyStack(s2)) //若命题变元匹配完成，操作符和字母栈中仍有元素，继续计算
    {
        res = Cal(s1, s2);
        PushStack(s2, res);
    }
    char ans = PopStack(s2); //取出答案
    freeStack(s1);
    freeStack(s2);
    // printf("\n");
    return ans;
}
void Find(L l, int now, int e, char str[]) //将str里的所有命题变元进行真值指派，now指当前到第几个变元，e为总共的变元数
{
    if (now > e) //若已经将所有命题变元都指派真值后
    {
        total++;                       //总数+1
        strcpy(ChangeStr[total], str); //存储
        return;                        //回到上一级
    }
    char str2[100], str3[100]; //存储原先的str
    strcpy(str2, str);
    strcpy(str3, str);

    int total = l[now].lengthe;     //该变元的所有位置
    for (int i = 0; i < total; i++) //所有位置都变
    {
        int p = l[now].elem[i];
        str2[p] = 'F';
    }
    Find(l, now + 1, e, str2);      //到下一个命题变元
    total = l[now].lengthe;         //该变元的所有位置
    for (int i = 0; i < total; i++) //所有位置都变
    {
        int p = l[now].elem[i];
        str3[p] = 'T';
    }
    Find(l, now + 1, e, str3); //找下一个命题变元
}
int Repeat(char str[], char ch) //在str中找ch是否已经出现过，如果已经出现，则返回其第一次出现的位置，未出现过则返回-1
{
    int len = strlen(str);
    for (int i = 0; i < len; i++)
    {
        if (ch == str[i])
            return i;
    }
    return -1;
}
L ProcessStr(char str[]) //处理原命题公式，计算所有可能的真值指派
{
    int len = strlen(str);
    char str2[100], str3[100] = "\0";
    strcpy(str2, str); //记录下原命题变元
    L l = InitList(len);
    //将该命题变元全部变为'F',方便判断真值，并记录下所有命题变元的位置
    for (int i = 0; i < len; i++)
    {
        if ((str[i] >= 'A' && str[i] <= 'Z') || (str[i] >= 'a' && str[i] <= 'z')) //找所有变元位置
        {
            int f = Repeat(str3, str[i]); //找第一个和str[i]相同的字母的位置
            if (f == -1)                      //如果该变元未出现过
            {
                cnt++;                                       //变元总数+1
                targetch[cnt - 1] = str[i];                  //存所有不相同的字母
                l[cnt].ch = str[i];                          //存该字母
                l[cnt].elem[l[cnt].lengthe++] = i;  
                pos[i] = cnt;                                //映射，第一个字母位置对应的cnt
            }
            else //若该变元不是第一次出现
            {
                l[pos[f]].elem[l[pos[f]].lengthe++] = i; //存该字母的所有位置（从0开始）
            }
        }
        str3[i] = str[i];
    }
    for (int i = 0; i < cnt; i++)
        printf("\t%c ", targetch[i]); //输出真值表的第一行，先将所有的命题变元输出
    printf("\t%s\n", str2);           // str2为原字符串
    Find(l, 1, cnt, str);            //str为改为FT字符串
    return l;                         //返回线性表数组，方便后序处理
}

//判断主析取、主合取范式
char *ChangeXiStr(char Xistr[], int cnt, L l) //根据变后的主析取范式，即该主析取范式变元全为F\T
{                                             //对应线性表l中字母和位置，将其修改存储
    char ans[100] = "\0";
    char tar; //目标范式
    int len = strlen(Xistr), lena = 0, p;
    for (int i = 1; i <= cnt; i++) //找所有的变元
    {
        tar = l[i].ch; //找到字母
        p = l[i].elem[0];
        if (Xistr[p] == 'F') //找真值
        {
            ans[lena++] = tar;
            ans[lena++] = '\'';
        }
        else
            ans[lena++] = tar;
        if (i<cnt)
        ans[lena++] = '0';
    }
    return ans;
}
char *ChangeHeStr(char Hestr[], int cnt, L l) //根据变后的主合取范式，即该主合取范式变元全为F\T
{                                             //对应线性表l中字母和位置，将其修改存储，操作与找主析取范式类似
    char ans[100] = "\0";
    char tar;
    int len = strlen(Hestr), lena = 0, p;
    for (int i = 1; i <= cnt; i++)
    {
        tar = l[i].ch; //找到字母
        p = l[i].elem[0];
        if (Hestr[p] == 'T') //找真值
        {
            ans[lena++] = tar;
            ans[lena++] = '\'';
        }
        else
            ans[lena++] = tar;
        if (i<cnt)
        ans[lena++] = '1';
    }
    return ans;
}
void FindZhu(int cnt, L l) //输出主析取范式、主合取范式
{
    char chxi[100], chhe[100];
    printf("主析取范式：\n");
    for (int i = 0; i < totalXi; i++) //将所有真值为T的命题公式进行处理，合成主析取范式
    {
        strcpy(chxi, ChangeXiStr(XiStr[i], cnt, l));
        if (i == 0) //处理输出格式
            printf("(%s)", chxi);
        else
            printf("1(%s)", chxi);
    }
    printf("\n主合取范式：\n");
    for (int i = 0; i < totalHe; i++) //将所有真值为F的命题公式进行处理，合成主析取范式
    {
        strcpy(chhe, ChangeHeStr(HeStr[i], cnt, l));
        if (i == 0) //处理输出格式
            printf("(%s)", chhe);
        else
            printf("0(%s)", chhe);
    }
}

//判断命题公式类型
void Devide(int panz, int panj)
{
    if (panz == 1) // panz为1，说明没有出现真值为F的公式
        printf("该命题公式为一个永真式\n");
    else if (panj == 1) // panj为1，说明没有出错真值为T的公式
        printf("该命题公式为一个永假式\n");
    else //说明T、F均出现
        printf("该命题公式为一个可满足式\n");
}

//输出真值表
L InputTrueTable(char str[])
{
    L l = ProcessStr(str); //处理str,并返回其位置
    panj = 1, panz = 1;
    for (int i = 1; i <= total; i++)
    {
        char res = Calculate(ChangeStr[i]); //计算该命题公式的真值
        if (res == 'T')
        {
            strcpy(XiStr[totalXi++], ChangeStr[i]);
            panj = 0; //则该命题公式不可能为一个永假式
        }
        else
        {
            strcpy(HeStr[totalHe++], ChangeStr[i]);
            panz = 0; //该命题公式不可能为一个用真式
        }

        for (int j = 1; j <= cnt; j++) //遍历所有变元，输出其指派的真值
        {
            int p;                   //该判断是看是否只有一个命题变元的否定或者只有一个变元
            p = l[j].elem[0];
            printf("\t%c ", ChangeStr[i][p]);
        }
        printf("\t%c\n", res);
    }
    return l;
}

//初始化输出界面
void initInput()
{
    printf("请输入一个命题公式：\n");
    printf("变量用字母表示（本程序区分大小写，即大写字母A和小写字母a不同）\n");
    printf("在字母后加上'表示该变量为非\n");
    printf("以下为命题符号表示\n");
    printf("0 ---- 合取\n");
    printf("1 ---- 析取\n");
    printf("2 ---- 条件\n");
    printf("3 ---双条件\n");
    printf("请注意输入命题公式的正确性！！！\n");
    printf("请输入您想要判断的命题公式：");
}
int main()
{
    char str[100];
    initInput();               //输出初始化界面
    scanf("%s", str);          //用户输入命题公式
    L l = InputTrueTable(str); //输出真值表
    Devide(panz, panj);        //输出该命题公式的类型
    FindZhu(cnt, l);           //输出其主析取范式、主合取范式
    freeList(l);               //释放存储空间
    return 0;
}