Python机器学习18——Xgboost和Lightgbm结合分位数回归(机器学习与传统统计学结合)_xgboost做分位数回归(3)

最新推荐文章于 2024-09-09 20:20:55 发布

m0_60667406

最新推荐文章于 2024-09-09 20:20:55 发布

阅读量706

点赞数 17

分类专栏： 2024年程序员学习文章标签：机器学习 python 回归

本文链接：https://blog.csdn.net/m0_60667406/article/details/137732324

版权

2024年程序员学习专栏收录该内容

277 篇文章 0 订阅

订阅专栏

先自我介绍一下，小编浙江大学毕业，去过华为、字节跳动等大厂，目前阿里P7

深知大多数程序员，想要提升技能，往往是自己摸索成长，但自己不成体系的自学效果低效又漫长，而且极易碰到天花板技术停滞不前！

因此收集整理了一份《2024年最新Python全套学习资料》，初衷也很简单，就是希望能够帮助到想自学提升又不知道该从何学起的朋友。

既有适合小白学习的零基础资料，也有适合3年以上经验的小伙伴深入学习提升的进阶课程，涵盖了95%以上Python知识点，真正体系化！

由于文件比较多，这里只是将部分目录截图出来，全套包含大厂面经、学习笔记、源码讲义、实战项目、大纲路线、讲解视频，并且后续会持续更新

如果你需要这些资料，可以添加V获取：vip1024c （备注Python）

正文

model_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True,}, 
                      lgb.Dataset(X_train, y_train), num_boost_round=100)

model_pred=model_lgb.predict(X_test)
mse_lgb.append(mean_squared_error(y_test,model_pred))
r2_lgb.append(r2_score(y_test,model_pred))

if alpha in [0.1,0.5,0.9]:
    qr_pred[alpha]=model_qr.predict(sm.add_constant(X_test))
    xgb_pred[alpha]=model_xgb.predict(xgb.DMatrix(X_test))
    lgb_pred[alpha]=model_lgb.predict(X_test)


分位点为0.1,0.5,0.9时记录一下，方便画图查看。


然后画出三种模型在不同分位点下的误差和拟合优度对比：

plt.figure(figsize=(7, 5),dpi=128)
plt.subplot(211)
plt.plot(alphas, mse_qr, label=‘Quantile Regression’)
plt.plot(alphas, mse_xgb, label=‘XGBoost’)
plt.plot(alphas, mse_lgb, label=‘LightGBM’)
plt.legend()
plt.xlabel(‘Quantile’)
plt.ylabel(‘MSE’)
plt.title(‘MSE across different quantiles’)

plt.subplot(212)
plt.plot(alphas, r2_qr, label=‘Quantile Regression’)
plt.plot(alphas, r2_xgb, label=‘XGBoost’)
plt.plot(alphas, r2_lgb, label=‘LightGBM’)
plt.legend()
plt.xlabel(‘Quantile’)
plt.ylabel(‘ $R^2$ ’)
plt.title(‘ $R^2$ across different quantiles’)
plt.tight_layout()
plt.show()


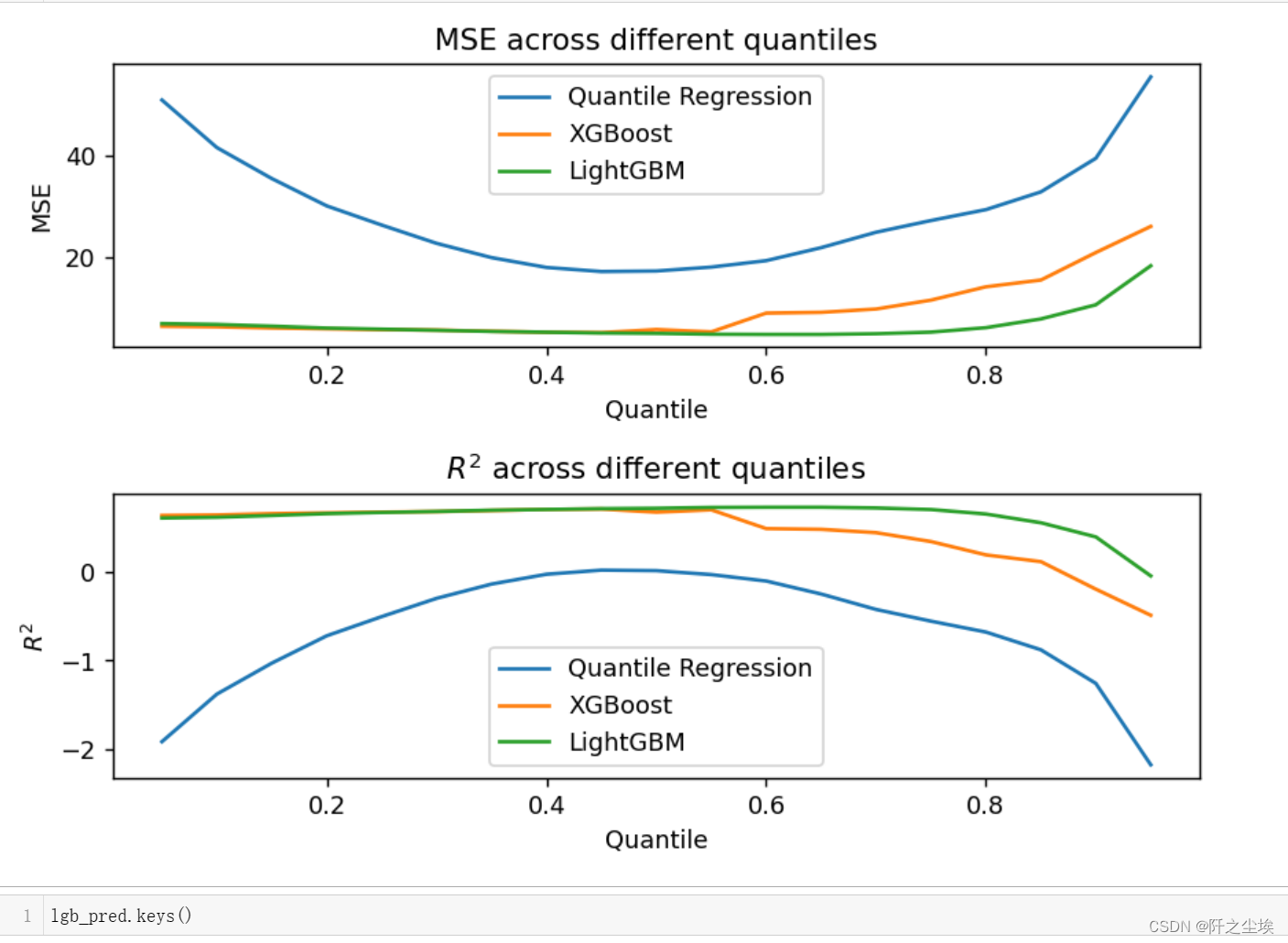
![](https://img-blog.csdnimg.cn/0df54f417b1f4d99875de56bde1840a4.png)


可以看到在分位点为0.5附件，模型的误差都比较小。因为这个数据集没有很多的异常值。然后模型表现上，LGBM>XGB>线性QR。线性模型对于一个非线性的函数关系拟合在这里当然不行。


画出拟合图：

name=[‘QR’,‘XGB-QR’,‘LGB-QR’]
plt.figure(figsize=(7, 6),dpi=128)
for k,model in enumerate([qr_pred,xgb_pred,lgb_pred]):
n=int(str(‘31’)+str(k+1))
plt.subplot(n)
plt.scatter(X_test,y_test,c=‘k’,s=2)
for i,alpha in enumerate([0.1,0.5,0.9]):
sort_order = np.argsort(X_test, axis=0).ravel()
X_test_sorted = np.array(X_test)[sort_order]
#print(np.array(model[alpha]))
predictions_sorted = np.array(model[alpha])[sort_order]
plt.plot(X_test_sorted,predictions_sorted,label=fr" $\tau$ ={alpha}",lw=0.8)
plt.legend()
plt.title(f’{name[k]}')
plt.tight_layout()
plt.show()


![](https://img-blog.csdnimg.cn/793d388430f1427eb1da1e23dae56c3c.png)


可以看到分位数回归的明显的区间特点。


还有非参数非线性方法的优势，明显XGB和LGBM拟合得更好。




---


#### 波士顿数据集


上面是人工数据，下面采用真实的数据集进行对比，就用回归最常用的波士顿房价数据集吧：

data_url = “http://lib.stat.cmu.edu/datasets/boston”
raw_df = pd.read_csv(data_url, sep=“\s+”, skiprows=22, header=None)
data = np.hstack([raw_df.values[::2, :], raw_df.values[1::2, :2]])
target = raw_df.values[1::2, 2]
column_names = [‘CRIM’,‘ZN’,‘INDUS’,‘CHAS’,‘NOX’,‘RM’,‘AGE’,‘DIS’,‘RAD’,‘TAX’,‘PTRATIO’, ‘B’,‘LSTAT’, ‘MEDV’]
boston=pd.DataFrame(np.hstack([data,target.reshape(-1,1)]),columns= column_names)


取出X和y，划分测试集和训练集

X = boston.iloc[:,:-1]
y = boston.iloc[:,-1]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


拟合预测，对比

alphas = np.arange(0.1, 1, 0.1)
mse_qr, mse_xgb, mse_lgb = [], [], []
r2_qr, r2_xgb, r2_lgb = [], [], []
qr_pred,xgb_pred,lgb_pred={},{},{}

Train and evaluate

for alpha in alphas:
# Quantile Regression
model_qr = QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)
model_pred=model_qr.predict(sm.add_constant(X_test))
mse_qr.append(mean_squared_error(y_test,model_pred ))
r2_qr.append(r2_score(y_test,model_pred))

# XGBoost
model_xgb = xgb.train({"objective": "reg:quantileerror", 'quantile_alpha': alpha}, 
                      xgb.QuantileDMatrix(X_train, y_train), num_boost_round=100)
model_pred=model_xgb.predict(xgb.DMatrix(X_test))
mse_xgb.append(mean_squared_error(y_test,model_pred ))
r2_xgb.append(r2_score(y_test,model_pred))

# LightGBM
model_lgb = lgb.train({'objective': 'quantile', 'alpha': alpha,'force_col_wise': True,}, 
                      lgb.Dataset(X_train, y_train), num_boost_round=100)

model_pred=model_lgb.predict(X_test)
mse_lgb.append(mean_squared_error(y_test,model_pred))
r2_lgb.append(r2_score(y_test,model_pred))

if alpha in [0.1,0.5,0.9]:
    qr_pred[alpha]=model_qr.predict(sm.add_constant(X_test))
    xgb_pred[alpha]=model_xgb.predict(xgb.DMatrix(X_test))
    lgb_pred[alpha]=model_lgb.predict(X_test)


画图查看不同分位点的不同模型的误差和拟合优度：

plt.figure(figsize=(8, 5),dpi=128)
plt.subplot(211)
plt.plot(alphas, mse_qr, label=‘Quantile Regression’)
plt.plot(alphas, mse_xgb, label=‘XGBoost’)
plt.plot(alphas, mse_lgb, label=‘LightGBM’)
plt.legend()
plt.xlabel(‘Quantile’)
plt.ylabel(‘MSE’)
plt.title(‘MSE across different quantiles’)


![](https://img-blog.csdnimg.cn/ae2bddc0b8134f229c1f665b3491f1a1.png)


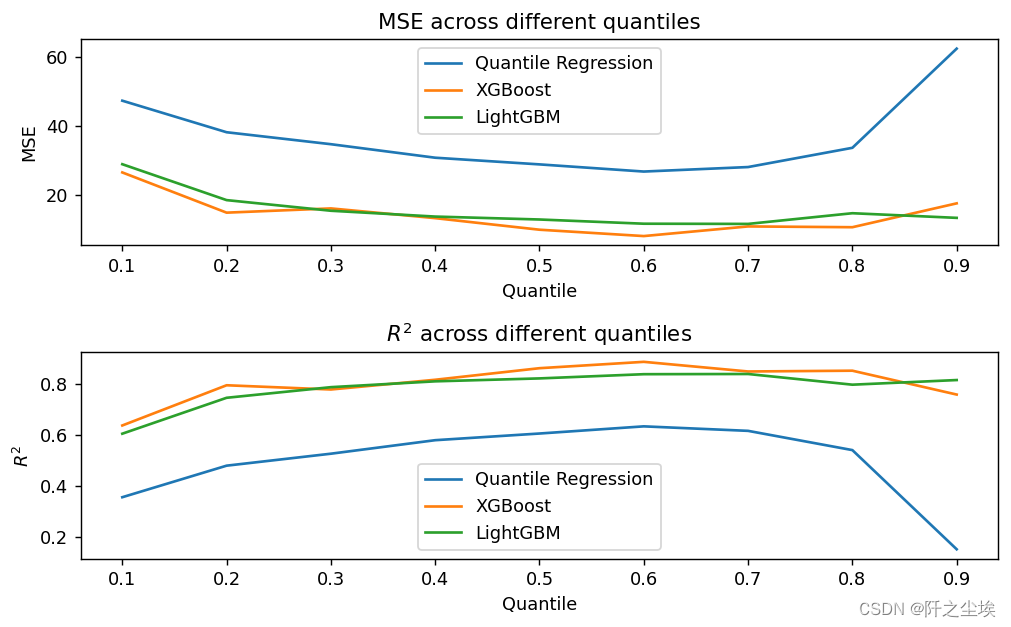
可以看到在分位点为0.6附件三个模型表现效果都比较好，然后模型表现来看，XGB>LGBM>QR，还是两个机器学习模型更厉害。




---


#### 分位数损失函数和平方和损失函数对比


上面我们得到在分位点为0.6的时候，模型效果表现好，那么分位数模型和普通的MSE损失函数的效果比起来怎么样呢?我们继续对比：

定义alpha值

alpha = 0.5

分位数回归模型

model_qr = sm.regression.quantile_regression.QuantReg(y_train, sm.add_constant(X_train)).fit(q=alpha)
qr_pred = model_qr.predict(sm.add_constant(X_test))

XGBoost分位数回归

model_xgb = xgb.train({“objective”: “reg:quantileerror”, ‘quantile_alpha’: alpha},
xgb.DMatrix(X_train, label=y_train), num_boost_round=100)
xgb_q_pred = model_xgb.predict(xgb.DMatrix(X_test))

LightGBM分位数回归

model_lgb = lgb.train({‘objective’: ‘quantile’, ‘alpha’: alpha,‘force_col_wise’: True},
lgb.Dataset(X_train, label=y_train), num_boost_round=100)
lgb_q_pred = model_lgb.predict(X_test)

普通的最小二乘法线性回归

model_lr = LinearRegression()
model_lr.fit(X_train, y_train)
lr_pred = model_lr.predict(X_test)

普通的XGBoost

model_xgb_reg = xgb.train({“objective”: “reg:squarederror”}, xgb.DMatrix(X_train, label=y_train), num_boost_round=100)
xgb_pred = model_xgb_reg.predict(xgb.DMatrix(X_test))

普通的LightGBM

model_lgb_reg = lgb.train({‘objective’: ‘regression’, ‘force_col_wise’: True}, lgb.Dataset(X_train, label=y_train), num_boost_round=100)
lgb_pred = model_lgb_reg.predict(X_test)


上面是六个模型，非别是基于分位数回归的XGB,LGBM,线性分位数回归。还有三个基于最普通的MSE损失函数的普通XGB,LGBM和最小二乘线性回归。


# 计算6个模型的MSE和R^2 





### 最后

> **🍅 硬核资料**：关注即可领取PPT模板、简历模板、行业经典书籍PDF。  
> **🍅 技术互助**：技术群大佬指点迷津，你的问题可能不是问题，求资源在群里喊一声。  
> **🍅 面试题库**：由技术群里的小伙伴们共同投稿，热乎的大厂面试真题，持续更新中。  
> **🍅 知识体系**：含编程语言、算法、大数据生态圈组件（Mysql、Hive、Spark、Flink）、数据仓库、Python、前端等等。




**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**需要这份系统化的资料的朋友，可以添加V获取：vip1024c （备注python）**
![img](https://img-blog.csdnimg.cn/img_convert/6dd60059fd6358799bac59a80b5054d8.png)

**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**
n、前端等等。




**网上学习资料一大堆，但如果学到的知识不成体系，遇到问题时只是浅尝辄止，不再深入研究，那么很难做到真正的技术提升。**

**需要这份系统化的资料的朋友，可以添加V获取：vip1024c （备注python）**
[外链图片转存中...(img-NOvQlSpA-1713039912101)]

**一个人可以走的很快，但一群人才能走的更远！不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人，都欢迎加入我们的的圈子（技术交流、学习资源、职场吐槽、大厂内推、面试辅导），让我们一起学习成长！**