王者之剑（最大权独立集）：概念

王者之剑

给出一个 $n\times m$ 网格，每个格子上有一个价值 $v_{i,j}$ 的宝石。

Amber 可以自己决定起点，开始时刻为第 $0$ 秒。

以下操作，在每秒内按顺序执行。

• 若第 $i$ 秒开始时，Amber 在 $(x,y)$，则 Amber 可以拿走 $(x,y)$ 上的宝石。
• 在偶数秒时（$i$ 为偶数），则 Amber 周围 $4$ 格的宝石将会消失。
• 若第 $i$ 秒开始时，Amber 在 $(x,y)$，则在第 $(i+1)$ 秒开始前，Amber 可以马上移动到相邻的格子 $(x+1,y),(x-1,y),(x,y+1),(x,y-1)$ 或原地不动 $(x,y)$。

求 Amber 最多能得到多大总价值的宝石。

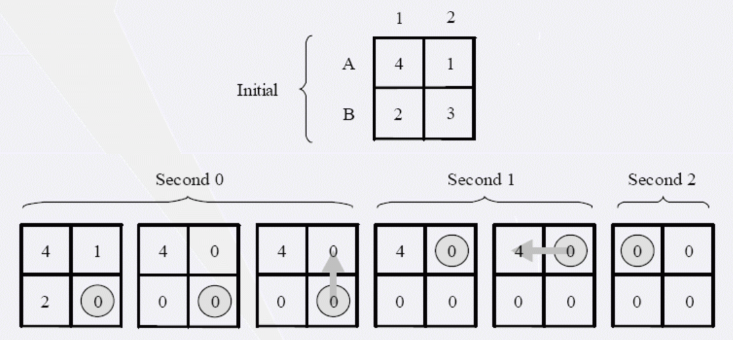
上图给出了一个 $2\times 2$ 的网格的例子。

在第 $0$ 秒，首先选择 $B2$ 进入，取走宝石 $3$；由于是偶数秒，周围的格子 $A2,B1$ 的宝石 $1,2$ 消失；向 $A2$ 走去。

在第 $1$ 秒，由于 $A2$ 的宝石已消失，无宝石可取；向 $A1$ 走去。

在第 $2$ 秒，取走 $A1$ 的宝石 $4$。

全程共取得 $2$ 块宝石：宝石 $3$ 和宝石 $4$。

输入格式

第一行包含两个整数 $n,m$。

接下来 $n$ 行，每行包含 $m$ 个整数，用来描述宝石价值矩阵。其中第 $i$ 行第 $j$ 列的整数表示 $v_{i,j}$。

输出格式

输出可拿走的宝石最大总价值。

数据范围

$1\le n,m\le 100$,
$1\le v_{i,j}\le 1000$

输入样例：

2 2
1 2
2 1

输出样例：

4

概念及题目思路

如果权值为 $1$ 的话，那就是二分图匈牙利算法的经典模型。

但本次说的不是权值为 $1$ 的情况。

概念：每两个点之间没有边，且每个点都有非负权值。

此时我们假设上图的红点是点覆盖集，其他点就是点覆盖集的补集。

此时我们大胆猜测 $V_2$ 就是独立集，下面我们就证明一下：

我们直接用反证法证简单些。

• 假设点覆盖集 $V_1$ 的补集 $V_2$ 不是独立集，说明 $V_2$ 中存在两个点 $u,v$ 之间存在一条边 $(u,v)$。由于 $V_1$ 同样是 $V_2$ 的补集，说明 $V_1$ 中一定不包含 $u,v$ 这两个点，那么 $(u,v)$ 这条边的两个点就都不在 $V_1$ 中，即 $V_1$ 不是一个点覆盖集，与条件矛盾，反证得出任意一个点覆盖集的补集都是一个独立集。
• 假设独立集 $V_2$ 的补集 $V_1$ 不是点覆盖集，就必然存在一条边 $(u,v)$，使得这条边的两个点 $u,v$ 都不在 $V_1$，即一定在 $V_2$ 中，也就说明 $V_2$ 中存在两个点 $u,v$ 之间是有边的，所以 $V_2$ 就不是一个独立集，反证得出任意一个独立集的补集都是一个点覆盖集。

然后我们还要有数量关系，因为二者关系互补，所以二者相加的权值等于总的权值，那么结论也就得证了。

本题思路

• 本题让我们选一个起点，每一秒都会进行三种操作，综合看来每一秒都能走一步或不走，从而形成各种各样的走法，然后需要求出一种走法使拿走的宝石总价值最大。特别注意的是，人可以上下左右或不动。

• 我们可以让这个人每走到一个格子，如果格子上有宝石，一定会拿走。（贪心策略）

• 根据上述说法以及模拟结果，我们发现它的性质（这点很重要，对于不会的题我们可以模拟试试有没有思路）：

   > 我们发现，只有在偶数秒拿宝石。（因为偶数秒会使上、下、左、右的格子上的宝石消失）
  
   > 不可能同时拿走相邻位置的宝石。（本人发现这里就有点像独立集了（相邻两点间没有边））
  

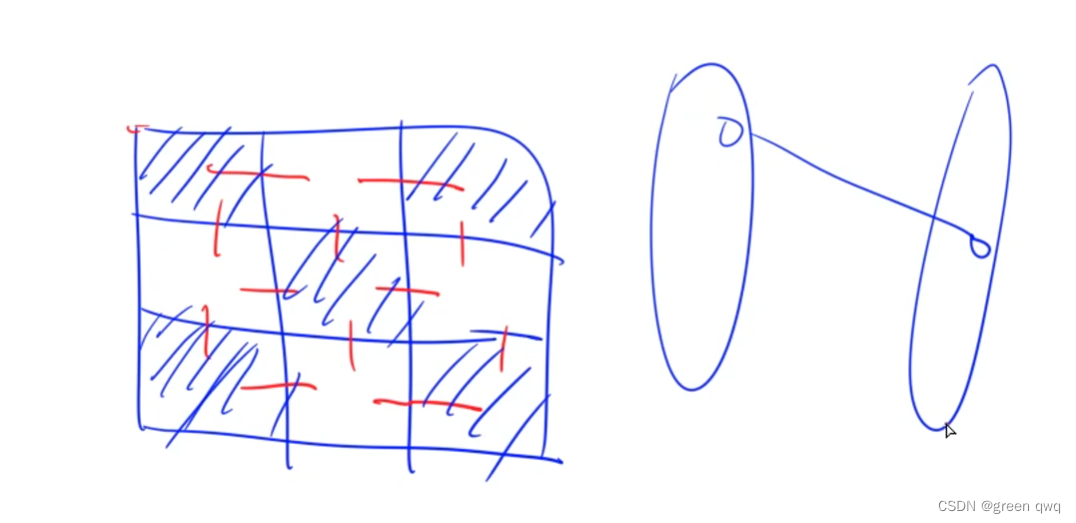
对于性质二：此时我们就可以把奇数的位置涂上黑色，其他位置为白色，然后把黑色位置点拿出来，白色位置也拿出来，这样就是二分图了。

因为这里我们觉得很像是独立集了，但不能直接做，我们得多想一步（但方向已经确定）。

现在就是证明独立集是不是能对应一种合法方案呢？

我们就奇数往前走，偶数不动（这是针对周围有宝石的情况，因为是周围嘛，我们直接就每次取两行就可以了），此时是一种合法方案。（即：可以从最左上角的一个有宝石的格子开始走，依次去取别的宝石，假设当前距离下一个宝石还剩两步，停下来判断一下，如果当前是偶数秒，直接走过去拿宝石，如果当前是奇数秒，原地停一秒再走过去拿宝石。且保证每次都优先取最近的宝石。这样的行走方案一定能将独立集中的所有宝石拿走，可以自行按照以上思路证明，这里的构造方式非常多，只要掌握好停顿一秒的精髓就能随便构造。）

细节：本题要把二维图转化成一维的标号，因此我们最好可以在图上标上 $1$ ~ $m$，这样方便看。

代码

//我们能发现刚刚解题所说的性质。最重要的性质就是：不可能同时拿走相邻位置的宝石，因此这就是
//很典型的二分图且是独立集问题

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;

const int N = 10010,M = (N*2+1010*2)*8+10,INT = 1e8;

int e[M],ne[M],f[M],h[N],idx;
int cur[N],d[N];
int n,m,S,T;
int dx[]={0,1,0,-1},dy[]={1,0,-1,0};
int tot;

int get(int x,int y){
    return (x-1)*m+y;
}

void add(int a,int b,int c){
    e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
    e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}

bool bfs(){
    queue<int>q;
    memset(d,-1,sizeof d);
    
    d[S]=0,cur[S]=h[S];
    
    q.push(S);
    
    while(q.size()){
        int t=q.front();
        q.pop();
        
        for(int i=h[t];~i;i=ne[i]){
            int ver=e[i];
            
            if(d[ver]==-1&&f[i]){
                d[ver]=d[t]+1;
                cur[ver]=h[ver];
                if(ver==T)return true;
                q.push(ver);
            }
        }
    }
    return false;
}

int find(int u,int lim){
    if(u==T)return lim;
    
    int flow=0;
    
    for(int i=cur[u];~i&&flow<lim;i=ne[i]){
        int ver=e[i];
        
        cur[u]=i;
        
        if(d[ver]==d[u]+1&&f[i]){
            int t=find(ver,min(f[i],lim-flow));
            if(!t)d[ver]=-1;
            f[i]-=t,f[i^1]+=t,flow+=t;
        }
    }
    return flow;
}

int dinic(){
    int r=0,flow;
    
    while(bfs())while(flow=find(S,INT))r+=flow;
    
    return r;
}

int main(){
    cin>>n>>m;
    
    memset(h,-1,sizeof h);
    
    S=0,T=n*m+1;
    
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            int x;
            cin>>x;
            if((i+j)&1){
                //如果是奇数的话
                add(S,get(i,j),x);
                for(int k=0;k<4;k++){
                    int a=dx[k]+i,b=dy[k]+j;
                    if(a<1||a>n||b<1||b>m)continue;
                    add(get(i,j),get(a,b),INT);
                }
            }else{
                add(get(i,j),T,x);
            }
            tot+=x;
        }
    }
    
    cout<<tot-dinic();
    
    return 0;
    
}