【模板】费用流：概念及证明过程

给定一个包含 $n$ 个点 $m$ 条边的有向图，并给定每条边的容量和费用，边的容量非负。

图中可能存在重边和自环，保证费用不会存在负环。

求从 $S$ 到 $T$ 的最大流，以及在流量最大时的最小费用。

输入格式

第一行包含四个整数 $n,m,S,T$。

接下来 $m$ 行，每行三个整数 $u,v,c,w$，表示从点 $u$ 到点 $v$ 存在一条有向边，容量为 $c$，费用为 $w$。

点的编号从 $1$ 到 $n$。

输出格式

输出点 $S$ 到点 $T$ 的最大流和流量最大时的最小费用。

如果从点 $S$ 无法到达点 $T$ 则输出 0 0。

数据范围

$2\le n\le 5000$,
$1\le m\le 50000$,
$0\le c\le 100$,
$-100\le w\le 100$
$S\ne T$

输入样例：

5 5 1 5
1 4 10 5
4 5 5 10
4 2 12 5
2 5 10 15
1 5 10 10

输出样例：

20 300

思路及推导

概念：所有最大可行流中，费用的最大/最小值。

公式：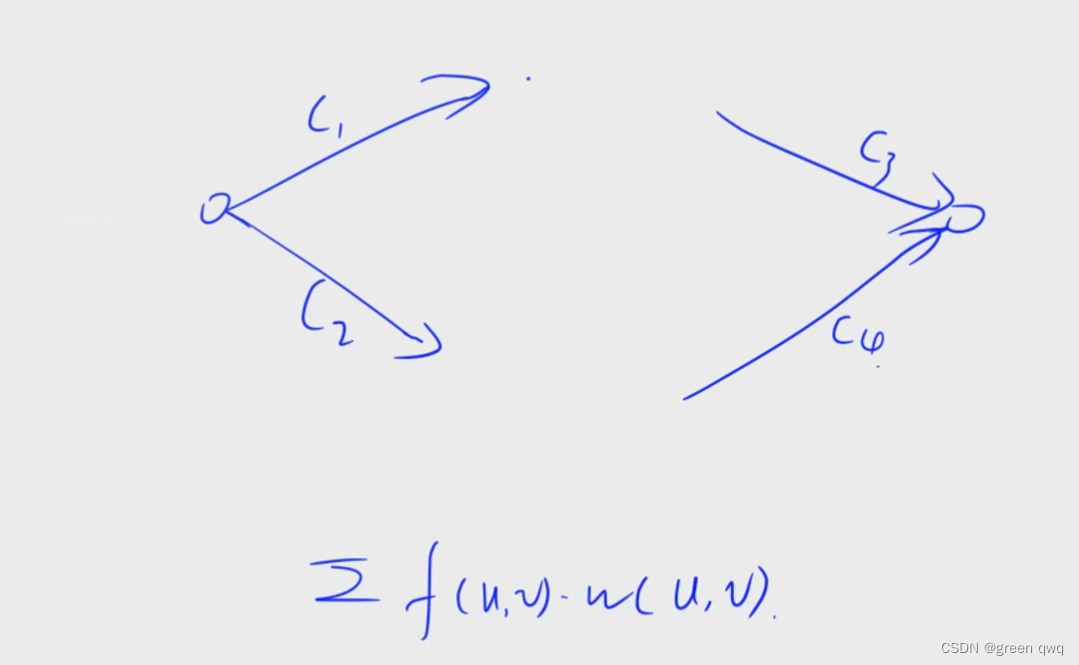
其中，$w$ 为费用。

拓展：可行流的流量不一定是从 $s$ 来的。

比如：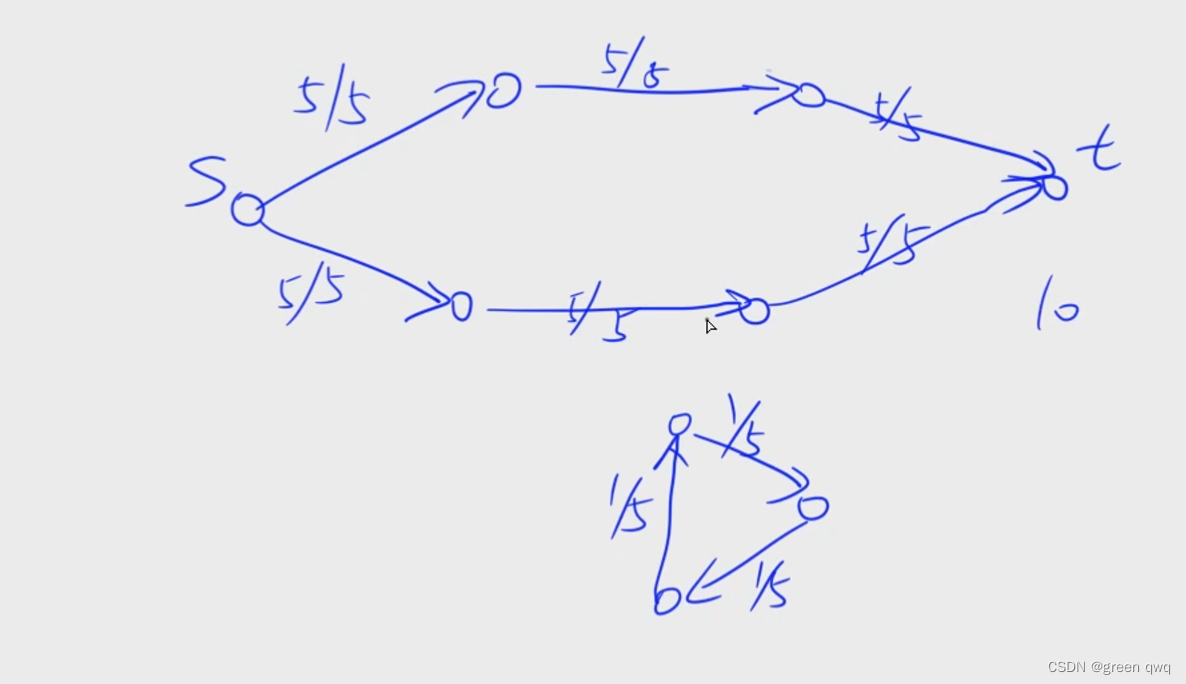
上图是张 $G$。满足容量限制和流量守恒。下面的网络流的流量可以任意但不影响最大流。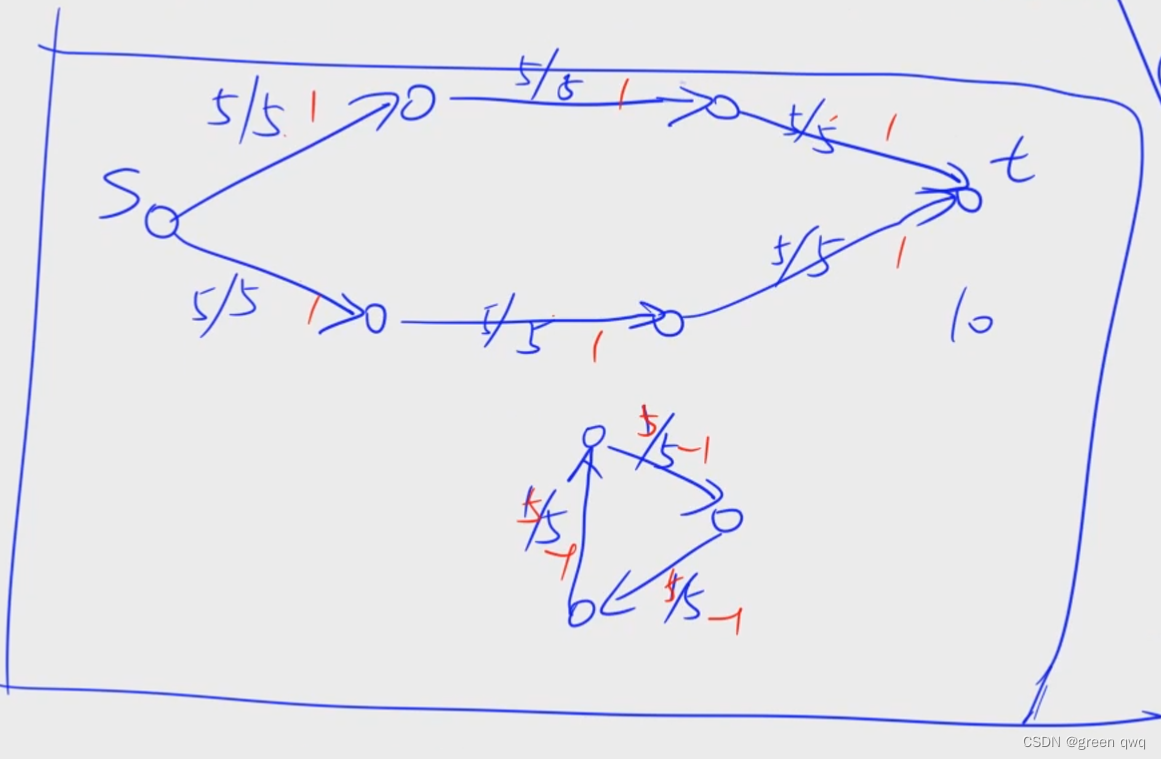
我们把费用标称成色，此时这张图的费用流为 $(1+1+1+1+1+1)\times 5+(-1)\times 3\times 5=15$。

做法：EK算法求，只不过把 bfs 改成 spfa。

证明：为什么这个做法是对的呢？
此时我们假设 $f_1$ 是费用最小的，$f_2$ 是最短路的，且 $f$ 不是费用最小的（这个是网络流，它们相加之和仍然费用流，因此等式是成立的）。我们假设 $|f^{\prime }|=|f|$（流量相等的意思），其中 $f^{\prime }$ 是费用最小的，我们把 $f^{\prime }-f_1$ 然后假设等于 $f_2^{\prime }$，那么此时：$f^{\prime }=f_1+f_2^{\prime }$ ，又因为 $|f^{\prime }|=|f|$，$|f_1|=|f_1^{\prime }|$，那么 $|f_2|=|f_2^{\prime }|$。又因为此时我们是设 $f^{\prime }$ 是费用最小的，那么我们可以推出：$f_2^{\prime }<f_2$（根据 $f_1|=|f_1^{\prime }|$ 和 $f=f_1+f_2$）那么此时我们就找到了更短的路径，就跟 $f_2$ 是最短路径就矛盾了，那么我们原始结论成立。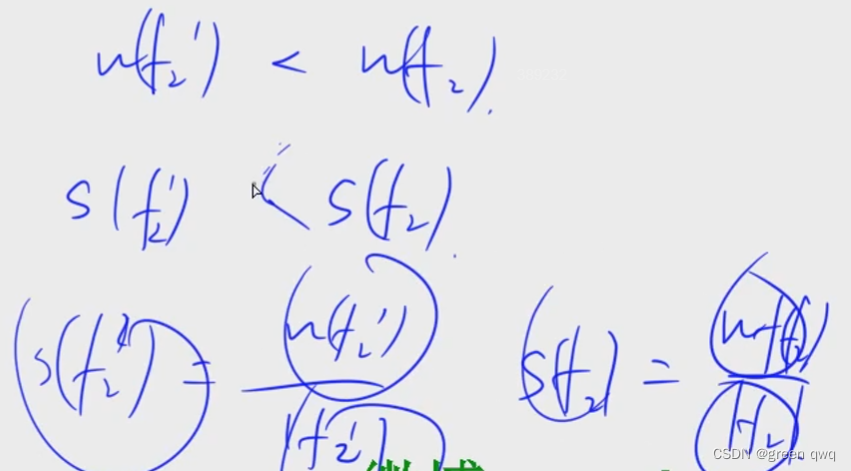

以上是费用流的公式。

spfa 得保证流网络没有负权边。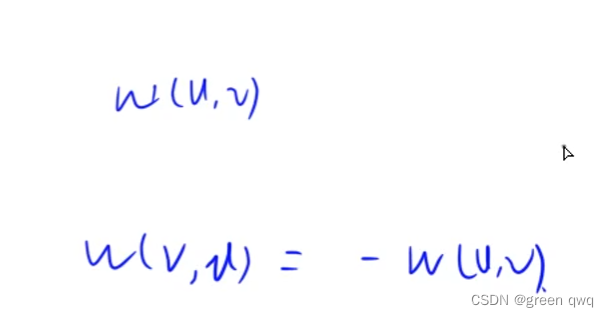
前面是正向边的费用。

后面是反向边的费用流。

为什么这样呢？就是要满足退流（退费）的性质。

下面用公式的原理来说：

可行流的费用:

$Cost(f_{u,v})=f(u,v)\ast w(u,v)$

退流的时候设费用为负就可以抵消这个费用的产生的贡献了。

$Cost(f_{u,v})=f(u,v)\ast w(u,v)+f(u,v)\ast (-w(u,v))=0$

如果要用负向边，我们得用到消圈法（存在负权回路的时候）。

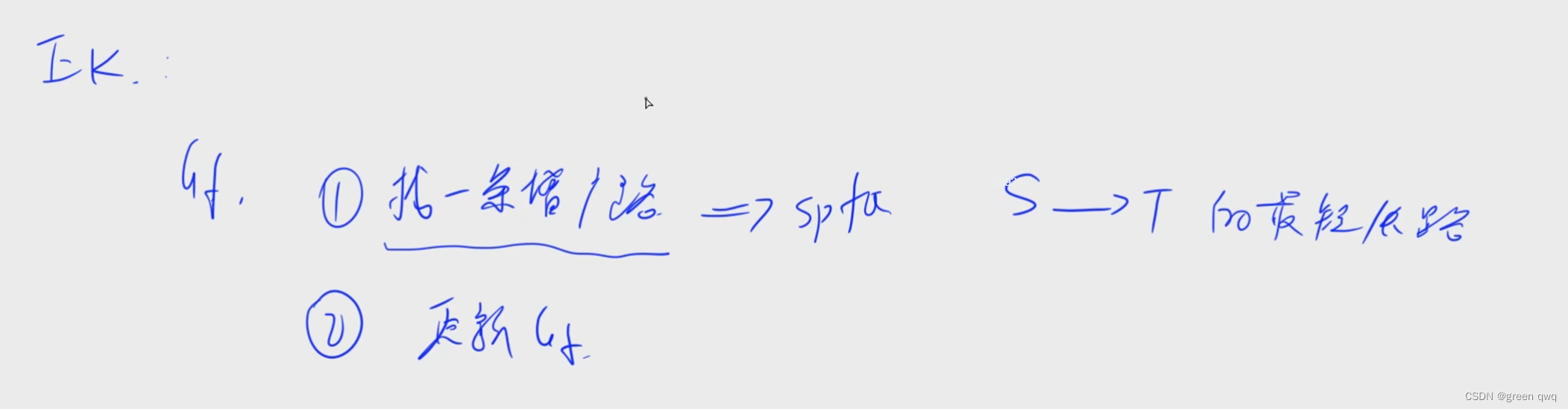
以上是费用流的流程。

拓展资料

消圈法

---

总的做法

用 while 循环不断判断残量网络中是否存在增广路径。

对于循环中：

• 找到增广路径。（只不过这边的相比 $EK$ 算法的 bfs 改成了 spfa）
• 更新残量网络。
• 累加最大流量。

循环结束，得出最大流和费用流。

---

代码

//EK算法

#include<iostream>
#include<algorithm>
#include<cstring>
#include<queue>

using namespace std;

const int N = 5010,M = 50000*2+10,INT = 1e8;

int e[M],ne[M],f[M],w[M],h[N],idx;
int d[N],incf[N],pre[N];//incf表示源点能传到每个节点的最大流量
bool st[N];
int n,m,S,T;

void add(int a,int b,int c,int d){
    e[idx]=b,f[idx]=c,w[idx]=d,ne[idx]=h[a],h[a]=idx++;
    e[idx]=a,f[idx]=0,w[idx]=-d,ne[idx]=h[b],h[b]=idx++;
}

bool spfa(){
    queue<int>q;
    q.push(S);
    
    memset(d,0x3f,sizeof d);
    
    memset(incf,0,sizeof incf);
    incf[S]=INT;
    
    d[S]=0;
    
    while(q.size()){
        int t=q.front();
        q.pop();
        st[t]=false;
        for(int i=h[t];~i;i=ne[i]){
            int ver=e[i];
            if(f[i]&&d[ver]>d[t]+w[i]){
                d[ver]=d[t]+w[i];
                pre[ver]=i;
                incf[ver]=min(f[i],incf[t]);
                
                if(!st[ver]){
                    st[ver]=true;
                    q.push(ver);
                }
            }
        }
    }
    return incf[T]>0;
}

void EK(int& flow,int& cost){
    flow=cost=0;
    
    while(spfa()){
        int t=incf[T];
        flow+=t,cost+=t*d[T];
        for(int i=T;i!=S;i=e[pre[i]^1]){
            f[pre[i]]-=t,f[pre[i]^1]+=t;
        }
    }
}

int main(){
    cin>>n>>m>>S>>T;
    
    memset(h,-1,sizeof h);
    
    for(int i=1;i<=m;i++){
        int a,b,c,d;
        cin>>a>>b>>c>>d;
        add(a,b,c,d);
    }
    
    int flow,cost;
    
    EK(flow,cost);
    
    cout<<flow<<" "<<cost;
    
    return 0;
    
}