【动态规划】高楼扔鸡蛋问题+延伸思考

Octopus--

已于 2022-08-08 11:41:57 修改

阅读量1.1k

点赞数 7

文章标签： c++ 动态规划动态规划求解

于 2022-02-24 21:14:19 首次发布

本文链接：https://blog.csdn.net/m0_60765523/article/details/122612992

版权

文章目录

题目
- 经典问题
- 推而广之
问题分析
解题方法
总结
参考

题目

经典问题

有一栋层数为1~100层的高楼，其中存在一个第k层，从这一层将鸡蛋扔下，恰好能够将鸡蛋摔碎（即低于这个楼层，鸡蛋一定摔不碎；高于这个楼层，鸡蛋则一定会摔碎），这个第k层称为临界楼层。
现给了你2个完全一样的鸡蛋，你可以把它们从任意一层楼扔下去。显而易见的，如果你把一个鸡蛋摔碎了，那它就没有了；如果鸡蛋没碎，那还可以捡起来继续扔。在最坏情况下，需要扔多少次鸡蛋才能确定这个临界楼层？

推而广之

假如楼高不是100层，而是任意的n层呢？
假如鸡蛋不是2个，而是3个？甚至任意的m个？

问题分析

首先明确一件事情：因为题目保证了临界楼层的存在性，因此，临界楼层最大不超过第100层。也就是说，鸡蛋从第100层扔下是肯定会碎的，相当于是题目中隐含的条件。信息完全未知的楼层只有99层。
很显然，这是一个有序的查找问题。
对于查找问题，最简单的就是遍历：从第1层开始扔下鸡蛋，如果没碎，那么依次测试2、3、4……，直到鸡蛋在第k层被摔碎。这固然是一个可行的方法，但是效率很低。在最坏情况下，临界楼层是100层，需要在1~99楼总共扔99次鸡蛋才能得到这一结果。当然，如果你只有1个鸡蛋，那么也就不得不采用这种朴素的办法。
对于这种有序的查找，最有效率的方法自然是二分查找。可惜的是，我们只有2个鸡蛋。假设临界楼层是100层，此时总共需要摔碎8个鸡蛋才能得到结果。虽然二分查找太过于浪费鸡蛋，但是我们可以借鉴其中的思想，采取折衷的策略，在2个鸡蛋的前提下，提高一点效率。
分段查找似乎是一个不错的选择。一个简单的思路是，每10层分一段，总共有10段。第一个鸡蛋依次从10，20，30，……，90层扔下，这样可以确定临界楼层在哪个区间，每个区间长度都是10；再用第二个鸡蛋遍历这个区间，就可以找到临界楼层。最坏情况下，临界楼层在99层或者100层，需要丢18次鸡蛋才能找到结果。
这个做法相比前面的大有长进，不过仍然有提升的空间。这个潜在的提升空间在于，如果第一个鸡蛋更早的碎了，那么有机会用更少的次数找到解；如果第一个鸡蛋碎的比较晚，那么在第一个鸡蛋上已经耗费了相当多的步数。如果能够平衡一下较好的情况和较差的情况，那么将会得到一个最坏情况下表现更好的算法。

解题方法

法一：数学推导

基于上述想法，提出一种思路：对于分段查找的区间，并不采用均匀的划分，而是从下往上每个区间的长度递减1。这样，当临界楼层所在的高度较高时，虽然定位这个区间需要花费更多的次数，但遍历这个区间需要的次数会少一些。¹

具体算法如下：

第一次从第 $x$ 层扔下鸡蛋。
如果碎了，那么可以确定临界楼层在 $[1, x]$ 这个区间，区间长度为 $x$ 。用第二个鸡蛋遍历第 $1$ 层到第 $x$ 层，寻找临界楼层。
如果没碎，那么下一个区间长度应该为 $x - 1$ 。即下一次在第 $x + x - 1 = 2 x - 1$ 层扔下鸡蛋。
如果碎了，可以确定临界楼层在 $[x + 1, 2 x - 1]$ 这个区间。
如果没碎，那么下一个区间长度应该为 $x - 2$ 。
……

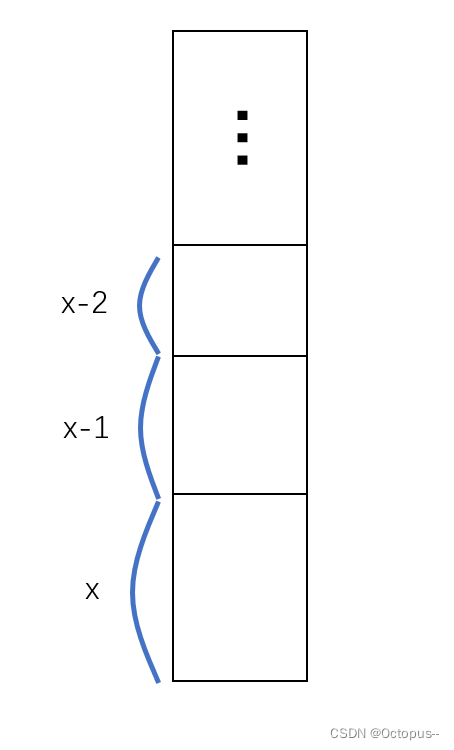
在这种划分方式下，无论临界楼层落在哪个区间，最坏情况下都能够以 $x$ 步找到。
用如下方程求出100层楼时对应的 $x$ （前面提到，因为题目保证了临界楼层的存在性，所以第100层的结果是已知的，完全未知的部分只有99层，因此只需大于等于99）：
$x + (x - 1) + (x - 2) + ... + 2 + 1 >= 99$
容易解得 $x = 14$ ，即最少需要14步，可以保证在最坏情况下找出临界楼层。

法二：动态规划算法

做到这里，我们的经典问题已经解决了。假如想要将题目推广到任意的楼高，也只需要修改上述方程的右边，即可得到结果。
但是，如果变成3个鸡蛋呢？
问题变得麻烦得多了：从第 $x$ 层扔下第一个鸡蛋，假如碎了，那我用剩下的两个鸡蛋去探索 $[1, x]$ 这个区间，到底需要多少步？假如没碎，下一个区间又应该设置为多长？
不过，想到这里，我们已经能够看出明显的动态规划特征：问题的解由若干个小规模的子问题的解组成。即：

第一次将鸡蛋从 $x$ 楼扔下，鸡蛋要么碎，要么没碎。
如果碎了，那么问题归约到：在 $[1, x]$ 楼层区间中、用2个鸡蛋寻找临界楼层。
如果没碎，那么问题归约到：在 $[x + 1, 100]$ 楼层区间中、用3个鸡蛋寻找临界楼层。
那么，当第一次将鸡蛋从 $x$ 楼扔下时，该问题的步数就是这两个子问题各自的最小步数取一个max，再+1（这个+1指的是第一次从 $x$ 楼扔鸡蛋）。
接下来就可以将问题逐层分解。
遍历所有可能的 $x$ ，即可找到整个问题的最小步数。

在这个思路下，来思考相应的状态转移方程，以及如何用程序实现。当拥有m个鸡蛋、楼层高度为n时:

定义函数 $w ors t (i, j)$ ，含义是拥有 $i$ 个鸡蛋、探索一个高度为 $j$ 的楼层区间，最坏情况下所需要的步数。
只有一个鸡蛋的时候，需要通过遍历找解，故 $w ors t (1, j) = j - 1$ （前面说过，因为解的存在性，所以从顶楼扔下鸡蛋是肯定会碎的，可以不扔）。
当楼高为1时，临界楼层只能为1，因此 $w ors t (i, 1) = 0$ 。
其他情况下，遍历所有的 $1\leq x \lt j$ ，计算所有的 $max\{worst(i-1,x),worst(i,j-x)\}+1$ ，取其中最小的一种方案为 $w ors t (i, j)$ 的值。
$w ors t (m, n)$ 即为问题的解。

状态转移方程：
$worst(i,j)=\left\{\begin{matrix}j-1，i=1\\0，j=1\\\min\{\max\{worst(i-1,x),worst(i,j-x)\}+1\}，其他，其中x=1,2,...,j-1 \end{matrix}\right.$
程序实现：

#include <iostream>
#include <algorithm>
#define num_of_eggs 3 // 鸡蛋的个数
#define height 100 // 楼层的高度

using namespace std;

int main()
{
    int worst[num_of_eggs + 1][height + 1];
    // 初始化
    for (int i = 0; i <= num_of_eggs; i++) {
        for (int j = 0; j <= height; j++) {
            worst[i][j] = 0;
        }
    }
	
	// 给 worst表的第一行赋初值
    for (int j = 1; j <= height; j++) {
        worst[1][j] = j - 1;
    }
	
	// 计算
    for (int i = 2; i <= num_of_eggs; i++) {
        for (int j = 2; j <= height; j++) {
            worst[i][j] = worst[i][j - 1] + 1;
            for (int k = 1; k < j; k++) {
                int temp = max(worst[i - 1][k], worst[i][j - k]) + 1;
                if (temp <= worst[i][j]) {
                    worst[i][j] = temp;
                }
            }            
        }
    }

    cout << worst[num_of_eggs][height] << endl;
    return 0;
}

这样可以轻松的算出，如果有3个鸡蛋，100层楼，最坏情况下的最小步数为9。m个鸡蛋，n层楼的任意情况，也可以轻松算出啦~
然而，这个方法的时空复杂度都不太理想，还有很明显的可以压缩的空间。该算法的时间复杂度为 $O(mn^2)$ ，空间复杂度为 $O (mn)$ 。为什么说还有明显的压缩空间呢？我们把上述的worst表打印一段出来看看：

楼层高度	2	3	4	5	6	7	8	9	10
1个鸡蛋	1	2	3	4	5	6	7	8	9
2个鸡蛋	1	2	2	3	3	3	4	4	4
3个鸡蛋	1	2	2	3	3	3	3	4	4

在拥有两个以上的鸡蛋时，每增加一层楼，最小步数可能+1，也可能不变，所以最后会形成一个0，1，2，2，…，2，3，3，…，3，4，4，…的序列，为了找到一个这么简单且有规律的序列，居然需要使用三次方时间复杂度的算法？我们可以用一些动态规划的小伎俩，比如说二分查找、参考前一次的决策等等来压缩一些时间，但这还不够。实际上，相比起研究探索给定的楼层需要多少步数，研究给定的步数能够探索多少楼层 ，是更有价值的！

法三：改进动态规划算法

自此，我们研究的问题已经改变了：我们拥有m个鸡蛋，至多允许扔k次，那么楼高至多为多少时，能够确保找到临界楼层？显然，随着步数的增长，可以探索的楼高是指数上升的，因此一定可以更快地找到原问题的解。
这个问题也可以用动态规划逐层分解：

假设拥有 $m$ 个鸡蛋，允许扔 $k$ 次，至多可以探索 $f (m, k)$ 层楼。
显然，类似法二中的分析，初始条件有 $f (1, k) = k + 1$ ， $f (m, 0) = 1$
其他情况下，如果第一次丢下鸡蛋就碎了，那么我们损失了一个步数、还损失了一个鸡蛋，因此还能探索 $f (m - 1, k - 1)$ 层楼，这就是下半段的最大楼高。
如果第一次丢鸡蛋没有碎，那么我们损失了一个步数、没损失鸡蛋，还能探索 $f (m, k - 1)$ 层楼，这就是上半段的最大楼高。
于是， $f (m, k) = f (m - 1, k - 1) + f (m, k - 1)$

状态转移方程：
$f(m,k)=\left\{\begin{matrix}k+1，m=1\\1，k=0\\f(m-1,k-1)+f(m,k-1)，其他\end{matrix}\right.$
动态规划2

程序实现：

#include <iostream>
#include <algorithm>
#define num_of_eggs 3 // 鸡蛋的个数
#define steps 9 // 至多可以测试的次数

using namespace std;

int main()
{
    int f[num_of_eggs + 1][steps + 1];
    // 初始化
    for (int i = 0; i <= num_of_eggs; i++) {
        for (int j = 0; j <= steps; j++) {
            f[i][j] = 0;
        }
    }

    // 赋初值
    for (int j = 0; j <= steps; j++) {
        f[1][j] = j + 1;
    }
    for (int i = 1; i <= num_of_eggs; i++) {
        f[i][0] = 1;
    }

    // 计算
    for (int i = 2; i <= num_of_eggs; i++) {
        for (int j = 1; j <= steps; j++) {
            f[i][j] = f[i - 1][j - 1] + f[i][j - 1];
        }
    }

    cout << f[num_of_eggs][steps] << endl;
    return 0;
}

可以算出3个鸡蛋、9次测试至多可以探索130层楼。任意m个鸡蛋、k次测试的结果也可以轻松算出~ 而且在方法二中需要3*130的表格才能完成的任务，在方法三中仅仅需要3*9的表格就可以完成！
可以看出，在这个程序的f表中，楼层的增长速度将是指数的。对于相同的询问：m个鸡蛋，n层楼，需要多少步数，仅需要 $O(m\log n)$ 的时空复杂度，相比起方法二，大大提升了性能。

法四：二进制串+组合数法

对于给定步数，至多能够探索多少楼层的问题，是否只能通过递推计算呢？有没有直接计算的方法？
回忆一下我们扔鸡蛋的策略：从某一层楼扔下鸡蛋，如果鸡蛋碎了，那么向下寻找临界楼层；如果鸡蛋没碎，那么向上寻找临界楼层。经历了一系列的尝试之后，会得到一系列的测试结果（例如：碎，没碎，没碎，没碎，碎，……）。每一次的测试结果决定了下一次尝试的方向（向上或向下），如果测试的结果足够，则可以确定临界楼层。
据此，不妨进行一个大胆的抽象：对于每一次测试，如果结果是鸡蛋碎了，那么记1，如果鸡蛋没碎，那么记0。由于我们只有m个鸡蛋，至多能够测试k次，因此最终得到一个长度为k的二进制串，且其中至多有m个1。这些合法二进制串与临界楼层的可能情况一一对应，因此只要算出符合上述要求的合法二进制串有多少个，就能知道m个鸡蛋、k步至多能够探索多少楼层。
结合例子说一下：假设我们拥有2个鸡蛋，至多可以扔3次。根据前面的讨论，容易知道至多可以探索7层楼。下面对所有合法二进制串逐一讨论：

000：
- 第一次从3楼扔下，没碎；
- 第二次从5楼扔下，没碎；
- 第三次从6楼扔下，没碎；
- 结论：临界楼层是第7层。
001：
- 第一次从3楼扔下，没碎；
- 第二次从5楼扔下，没碎；
- 第三次从6楼扔下，碎了；
- 结论：临界楼层是第6层。
010：
- 第一次从3楼扔下，没碎；
- 第二次从5楼扔下，碎了；
- 第三次从4楼扔下，没碎；
- 结论：临界楼层是第5层。
011：
- 第一次从3楼扔下，没碎；
- 第二次从5楼扔下，碎了；
- 第三次从4楼扔下，碎了；
- 结论：临界楼层是第4层。
100：
- 第一次从3楼扔下，碎了；
- 第二次从1楼扔下，没碎；
- 第三次从2楼扔下，没碎；
- 结论：临界楼层是第3层。
101：
- 第一次从3楼扔下，碎了；
- 第二次从1楼扔下，没碎；
- 第三次从2楼扔下，碎了；
- 结论：临界楼层是第2层。
110：
- 第一次从3楼扔下，碎了；
- 第二次从1楼扔下，碎了；
- 两个鸡蛋用完了，测试结束，虽然序列后面还有，但一定全都是0，略去不管即可，可以看作是用来补位的0。
- 结论：临界楼层是第1层。

根据组合数的知识，我们不需要枚举就可以算出合法二进制串的数量： $C_3^0+C_3^1+C_3^2=1+3+3=7$ 。
如果你还不太服气，可以多算几个结果：（其实我也不是很服气，但是看着真挺有那么回事的）
2个鸡蛋，测试14次（熟悉的原始问题）： $C_{14}^0+C_{14}^1+C_{14}^2=1+14+91=106$
3个鸡蛋，测试9次（原始问题的推广，100层楼用3个鸡蛋最坏情况需要9次）： $C_9^0+C_9^1+C_9^2+C_9^3=1+9+36+84=130$
这些数字都可以在方法二和方法三的程序中得到验证。
结论： m个鸡蛋，k次测试，至多可以探索 $C_{k}^0+C_{k}^1+C_{k}^2+...+C_{k}^{m}$ 层楼。
PS：根据这个公式，可以验证方法三中的递推公式噢~
$\begin{aligned} f(m-1,k-1)&=C_{k-1}^0+C_{k-1}^1+C_{k-1}^2+...+C_{k-1}^{m-1}\\ f(m,k-1)&=C_{k-1}^0+C_{k-1}^1+C_{k-1}^2+...+C_{k-1}^{m-1}+C_{k-1}^{m} \end{aligned}$
$\begin{aligned} f(m-1,k-1)+f(m,k-1)&=C_{k-1}^0+(C_{k-1}^0+C_{k-1}^1)+(C_{k-1}^1+C_{k-1}^2)+...+(C_{k-1}^{m-1}+C_{k-1}^{m})\\ &=C_{k}^0+C_{k}^1+C_{k}^2+...+C_{k}^{m}\\ &=f(m,k) \end{aligned}$
这个办法在小规模的用例上体现出巨大的优势，可以不用打表、直接计算。不过在大规模的用例上，因为编程计算组合数在实质上也是依靠递推，所以相比起方法三，时间和空间复杂性上带来的提高应该不大。