【数据结构】期末笔记，超全！

Chap2 Array

SparseMatrix FastTranspose2(){
        SparseMatrix b(cols,rows,terms);
        if(terms > 0){
            int* rowStart = new int[cols];
            fill(rowStart,rowStart+cols,0);
            for(int i = 0;i < terms;i++){
                rowStart[smArray[i].col]++; 
            }          
            int rs = 0, valNow = 0;
            for (int i = 0; i < cols; i++)
            {
            	valNow = rowStart[i];
            	rowStart[i] = rs;
            	rs += valNow;
            }
            for(int i = 0;i < terms;i++){
                int j = rowStart[smArray[i].col];
                b.smArray[j].row = smArray[i].col;
                b.smArray[j].col = smArray[i].row;
                b.smArray[j].value = smArray[i].value;
                rowStart[smArray[i].col]++;
            }
            delete[] rowStart;
        }
        return b;
    }

Chap5 Tree

树的存储结构

广义表表示

按广义表的格式读入，然后建树

优点：可以对已经写好的用来操作广义表的通用函数进行复用

左孩子右兄弟

typedef struct CSNode{
	TElemetype data;
	struct CSNode* firstchild,*rightsib;
}CSNode,*CSTree;

优点：

• 找孩子方便，从firstchild找到长子，然后通过rightsib即可找到具体的孩子
• 把一棵复杂的树变成了一棵二叉树
  缺点：
• 找父节点不方便，但是可以添加一个parent指针域

双亲表示法

#define MAX_TREE_SIZE 100
typedef int TElemType;
typedef struct PTNode{
	TElemType data;//结点数据
	int parent;//双亲下标
}PTNode;
typedef struct{
	PTNode nodes[MAX_TREE_SIZE];
	int r,n;//根的位置和结点数
}PTree;

可以添加：长子域，兄弟域等等

二叉树

理论

存储结构

顺序存储

用一维数组存储二叉树中的结点，并且结点的存储位置即数组的下标要能体现结点之间的逻辑关系

• 一般只用于满二叉树，按二叉树的编号
• 其他二叉树也可存，空节点用其他字符代替，但容易造成存储空间的浪费

二叉链表存储

template<class T> class TreeNode;

template<class T>
class BinaryTree{

public:
    BinaryTree(){root = nullptr;}
    BinaryTree(TreeNode<T>* root){
        this->root = root;
    }
    BinaryTree copy(TreeNode<T>* origNode){
        if(!origNode) return 0;
        root = new TreeNode<T>* (origNode->self,copy(origNode->left),copy(origNode->right));
    }
    ~BinaryTree(){
        while(root){
            delete root->right;
            delete root->left;
            delete root;
        }
    }
    bool isEmpty(){
        return root==nullptr;
    }
    BinaryTree(BinaryTree<T>& bt1,T& item,BinaryTree<T>& bt2){//root:item,leftSubTree:bt1,rightSubTree:bt2
        root->self = item;
        root->left = bt1;
        root->right = bt2;
    }
    BinaryTree<T> leftSubTree(){
        return root->left;
    }
    BinaryTree<T> rightSubTree(){
        return root->right;
    }
    T rootData(){
        return root->self;
    }


    TreeNode<T>* getRoot(){
        return root;
    }

    TreeNode<T>* newNode(T t){
        TreeNode<T>* node = new TreeNode<T>;
        node->self = t;
        node->left = node->right = nullptr;
        return node;
    }
 
    void insertNode(TreeNode<T>*& root,int x){
        if(root == nullptr){
            root = newNode(x);
            return;
        }
        if(root->self > x){
            insertNode(root->left,x);
        }else{
            insertNode(root->right,x);
        }
    }

    void create(int data[],int n){
        root = nullptr;
        for(int i = 0;i < n;i++){
            insertNode(root,data[i]);
        }
    }
private:
    TreeNode<T>* root;
};


template<class T>
class TreeNode{
template<class T1> 
friend class BinaryTree;
public:
    TreeNode(T c){
        self = c;
    }
	TreeNode(){}
    
private:
    TreeNode<T>* left;
    TreeNode<T>* right;
    T self;
};

遍历

前缀/中缀/后缀表达式可以通过前序/中序/后序遍历二叉树的方式来实现

递归

	void inOrder(TreeNode<T>* currentNode){
        if(currentNode){
            inOrder(currentNode->left);
            cout<<currentNode->self<<" ";
            inOrder(currentNode->right);
        }   
    }
    
    void preOrder(TreeNode<T>* currentNode){
        if(currentNode){
            cout<<currentNode->self<<" ";
            preOrder(currentNode->left);         
            preOrder(currentNode->right);
        }   
    }
    
    void postOrder(TreeNode<T>* currentNode){
        if(currentNode){
            postOrder(currentNode->left);         
            postOrder(currentNode->right);
            cout<<currentNode->self<<" ";
        }   
    }

迭代

void nonrecInOrder(){
        if(root == nullptr) return;
        stack<TreeNode<T>*> s;
        TreeNode<T>* currentNode = root;
        while (1)
        {
            while(currentNode){
                s.push(currentNode);
                currentNode = currentNode->left;
            }
            if(s.empty()) return;
            currentNode = s.top();
            s.pop();
            cout<<currentNode->self<<" ";
            currentNode = currentNode->right;
        }
    }
    
    void nonrecPreOrder(){
        if(root == nullptr) return;
        stack<TreeNode<T>*> stk;
        TreeNode<T>* node = root;
        while(!stk.empty() || node!=nullptr){
            while(node != nullptr){
                cout<<node->self<<" ";
                stk.emplace(node);
                node = node->left;
            }
            node = stk.top();
            stk.pop();
            node = node->right;
        } 
    }

    void nonrecPostOrder(){
        if(root == nullptr) return;
        stack<TreeNode<T>*> stk;
        TreeNode<T>* prev = nullptr;
        while(root!=nullptr || !stk.empty()){
            while(root != nullptr){
                stk.emplace(root);
                root = root->left;
            }
            root = stk.top();
            stk.pop();
            if(root->right == nullptr || root->right==prev){
                cout<<root->self<<" ";
                prev = root;
                root = nullptr;
            }else{
                stk.emplace(root);
                root = root->right;
            }
        }
    }

Analysis of NonrecInorder:(n is the number of nodes in the tree)

• time:O(n)
• space: the depth of the tree

层序遍历

利用queue来实现

void levelOrder(){
        queue<TreeNode<T>*> q;
        TreeNode<T>* currentNode = root;
        while(currentNode){
            cout<<currentNode->self<<" ";
            if(currentNode->left) q.push(currentNode->left);
            if(currentNode->right) q.push(currentNode->right);
            if(q.empty()) return;
            currentNode = q.front();
            q.pop();
        }
    }

由遍历结果确定一棵二叉树

• 由前序遍历和中序遍历结果，可以唯一确定一棵二叉树
• 由后序遍历和中序遍历结果，可以唯一确定一棵二叉树
  因此，可以出由二推一的题目。

前序+中序

1. 根据前序序列的第一个元素建立根结点；
2. 在中序序列中找到该元素，确定根结点的左右子树的中序序列；
3. 在前序序列中确定左右子树的前序序列；
4. 由左子树的前序序列和中序序列建立左子树；
5. 由右子树的前序序列和中序序列建立右子树。
   

struct node{
	int data;
	node* lchild;
	node* rchild;
};

node* create(int preL,int preR,int inL,int inR){
	if(preL > preR) return nullptr;
	node* root = new node;
	root.data = pre[preL];
	int k;
	for(k = inL;k <= inR;k++){
		if(in[k]==pre[preL]){
			break;
		}
	}
	int numLeft = k-inL;
	root.lchild = create(preL+1,preL+numLeft,inL,k-1);
	root.rchild = create(preL+numLeft+1,preR,k+1,inR);
	return root;
}

后序+中序

1. 根据后序序列的最后一个元素建立根结点；
2. 在中序序列中找到该元素，确定根结点的左右子树的中序序列；
3. 在后序序列中确定左右子树的后序序列；
4. 由左子树的后序序列和中序序列建立左子树；
5. 由右子树的后序序列和中序序列建立右子树。

把输入纯作为字符串来处理，没有构建树的结构，只是单纯由后序+中序得到前序遍历的输出
https://www.luogu.com.cn/problem/P1030

#include<iostream>
#include<cstdio>
#include<cstring>

using namespace std;

const int maxn=15;

char s1[maxn],s2[maxn];
int length;

int findchar(char c)
{
	for(int i=0;i<length;i++)
	{
		if(c==s1[i]) return i;
	}
}

void dfs(int l1,int r1,int l2,int r2)
{
	int add=findchar(s2[r2]);
	cout<<s2[r2];
	//固定的起始点加上相同的长度
	if(add>l1) dfs(l1,add-1,l2,l2+add-1-l1);
    if(add<r1) dfs(add+1,r1,r2-1-r1+add+1,r2-1);
    
    //if(add>l1) dfs(l1,add-1,l2,r2-r1+add-1);
    //if(add<r1) dfs(add+1,r1,l2-l1+add,l2-l1+add+r1-add-1);
    //r1-add是当前这次切割后右子树的大小，r2-1是当前这次切割后右子树的结束下标，后者-前者则是当前这次切割后左子树的结束下标
}

int main()
{
	cin>>s1;//mid
	cin>>s2;//post
	length=strlen(s1)-1;
	dfs(0,length,0,length);
	return 0;
}

由后序+中序得到层序遍历结果

层序+中序

1. 根据层序遍历的特点，层序序列中第一个元素就是根节点root；
2. 确定该节点在中序序列中的位置。则该位置左边的都是左子树，右边都是右子树；
3. 左子树的根节点就是root的左孩子，右子树的根节点就是root的右孩子；
4. 递归到左子树和右子树；
5. 一直递归，便确定了每个节点的左右孩子。

struct T{
	int l,r;
}a[N];

int build(int il,int ir) //##核心函数：递归实现寻找每个节点的左右孩子
{
	int root,k;
	for(int i=1;i<=n;i++){ 
	//中序数列il到ir位置的数中，第一个在层序数列中出现的就是根节点 
		if(mp[floor[i]]>=il&&mp[floor[i]]<=ir){
			root=floor[i];
			break;
		}
	}
	k=mp[root];
	
	//k>il，根节点左边有位置，说明有左子树
	if(k>il) a[root].l=build(il,k-1); //中序数列中根节点root位置左边的是左子树 
	if(k<ir) a[root].r=build(k+1,ir);
	
	return root; //返回的是根节点！（作为其父树的左孩子或者右孩子）
}

void print(int x) //先序输出
{
	cout<<x<<" ";
	if(a[x].l) print(a[x].l);
	if(a[x].r) print(a[x].r);
}

int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		cin>>in[i]; //输入中序序列
		mp[in[i]]=i; //记录位置
	}
	for(int i=1;i<=n;i++) cin>>floor[i]; //输入层序序列
	
	build(1,n); //建树
	print(floor[1]); //先序输出
	return 0;
}

二叉树的建立

线索二叉树

基本概念

目的：

• 利用起来空指针域:n个结点的二叉树链表有2n个指针域，但只有n-1条分支数，因此有n+1个空指针域
• 在创建时记录下来前驱和后继

线索化

• 对二叉树以某种次序遍历使其变为线索二叉树
• 实质是在遍历的过程中修改空指针

每个结点应增设两个标志域（bool）:ltag,rtag
(教材里是leftthread,rightthread)

• 0表示指向左/右孩子
• 1表示指向前驱/后继

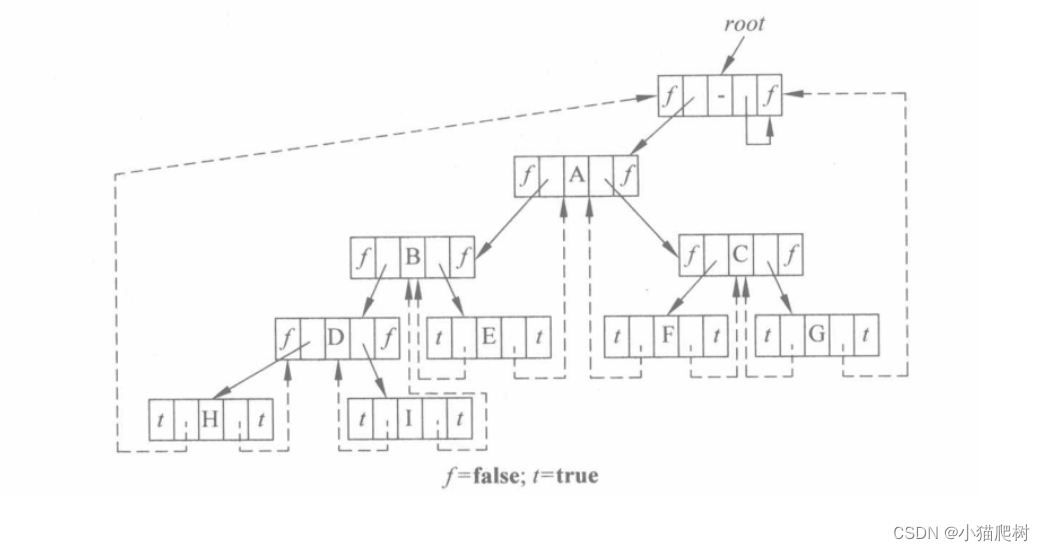
中序线索树举例

可以看到，图中H的leftChild和G的rightChild线索是悬挂着的。
为了不留下悬挂的线索，可为线索二叉树设置一个头节点，原来的二叉树为头节点的左子树。

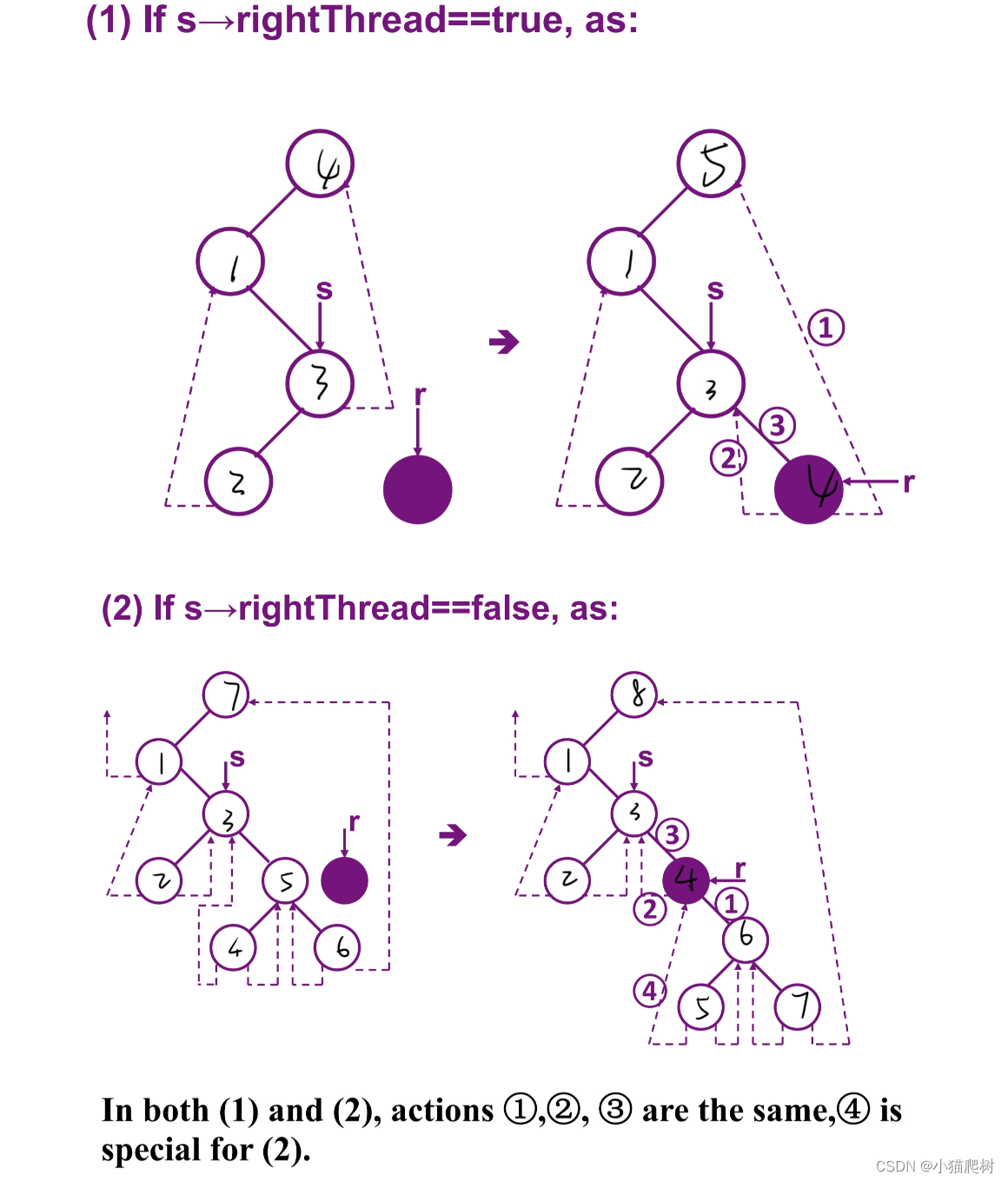
插入结点

（以作为右结点插入为例）
插入的情况有：

1. 如果s的右子树为空
2. 如果s的右子树非空

图示

把二叉树转化为中序线索树

#include<iostream>
#include<stack>
#include<string>
using namespace std;

template<class T> class ThreadedTreeNode;  

template<class T>
class ThreadedBinaryTree{

public:
    ThreadedBinaryTree(){root = nullptr;}
    bool isEmpty(){
        return root==nullptr;
    }
    ThreadedBinaryTree(ThreadedBinaryTree<T>& bt1,T& item,ThreadedBinaryTree<T>& bt2){
    //construct a binary tree，root:item，leftSubTree:bt1，rightSubTree:bt2
        root = new ThreadedTreeNode<T>*(item);
        root->left = bt1.root;
        root->right = bt2.root;
    }
    ThreadedBinaryTree<T> leftSubTree(){
        return root->left;
    }
    ThreadedBinaryTree<T> rightSubTree(){
        return root->right;
    }
    T rootData(){
        return root->self;
    }
    
    void insertRight(ThreadedTreeNode<T>* s,ThreadedTreeNode<T>* r){
    //insert r as the right child of s
        r->right = s->right;
        r->rightThread = s->rightThread;
        r->left = s;
        r->leftThread = true;
        s->right = r;
        s->rightThread = false;
        if(!r->rightThread){
            ThreadedTreeNode<T>* temp = next(r);
            temp->left = r;

        }
    }
	//make a binary tree into an inorder threaded binary tree
    void Threading(ThreadedBinaryTree<T> p){
        if(p){
            Threading(p.leftSubTree());
            if(p.leftSubTree()){
                p.root->leftThread = 1;
                p.root->left = pre;
            }
            if(!pre.right){
                pre.rightThread = 1;
                pre.rightThread = p;
            }
            pre = p;
            Threading(p.rightSubTree());
        }
    }

private:
    ThreadedTreeNode<T>* root;
    static ThreadedTreeNode<T> pre;
};

template<class T>
class ThreadedTreeNode{
template <class T1>
friend class ThreadedBinaryTree;
public:
    ThreadedTreeNode(char c){
        self = c;
    }
    ThreadedTreeNode(){}
    ThreadedTreeNode<T>* getRight(){
        return this->right;
    }
    ThreadedTreeNode<T>* getLeft(){
        return this->left;
    }

private:
    ThreadedTreeNode<T>* left;
    ThreadedTreeNode<T>* right;
    bool leftThread;
    bool rightThread;
    char self;
};

int main()
{
    return 0;
}

堆

堆是一棵顺序存储的完全二叉树

• 每个结点的关键字都不大于其孩子结点的关键字的堆，称为小根堆
• 每个结点的关键字都不小于其孩子结点的关键字的堆，称为大根堆

大顶堆

插入（对应代码中的pushIn）

删除（对应代码中的popOut）

template<class T>
class MaxHeap{
public:
    MaxHeap(int cap = 10){
        if(cap < 10) throw "Capacity must be >=1";
        capacity = cap;
        heapsize = 0;
        heap = new T[capacity+1];//!!heap[0] not used
    }
    bool isEmpty(){
        return heapsize==0;
    }
    T& getTop(){
        if(isEmpty()) throw"heap is empty";
        return heap[1];
    }
    void pushIn(const T& e){
        if(heapsize == capacity){
            T* newHeap = new T[2*capacity];
            copy(heap,heap+capacity,newHeap+1);
            capacity *= 2;
            delete[] heap;
            heap = newHeap;
        }
        int currentNode = ++heapsize;
        while(currentNode!=1 && heap[currentNode/2] < e){
	    //bubble up
            heap[currentNode] = heap[currentNode/2];
            currentNode /= 2;
        }
        heap[currentNode] = e;
    }
    void popOut(){
        if(isEmpty()) throw "Heap is empty. Cannot delete.";
        heap[1].~T();//delete the max
        //remove the last element from the heap
        T lastE = heap[heapsize--];//the last node

		//trickle down
        int currentNode = 1;//root
        int child = 2;//left child of currentNode
        while(child < heapsize){
	        //child always points to the larger child
            if(child<heapsize && heap[child]<heap[child+1]) child++;
            //can wput lastE in currentNode?
            if(lastE>heap[child]) break;//yes
            //no
            heap[currentNode] = heap[child];//move child up
            currentNode = child;
            child *= 2;//move down a level
        }
        heap[currentNode] = lastE;
    }
    
private:
    T* heap;
    int heapsize;
    int capacity;
};

Analysis:
pushIn()算法的时间复杂度为O(logn)

创建–两种方法

1. 创建一个空堆，然后挨个元素插入
2. 将n个元素先顺序放入一个二叉树中，形成一个完全二叉树，然后通过调整各结点的位置来实现

  void create_max_heap(void){
        int total = (*heap).key;
        /// 求倒数第一个非叶子结点
        int child = 2,parent = 1;
        for (int node = total/2; node>0; node--) {
            parent = node;
            child = 2*node;
            int max_node = 2*node+1;
            element temp = *(heap+parent);
            for (; child <= total; child *= 2,max_node = 2*parent+1) {
                if (child+1 <= total && (*(heap+child)).key < (*(heap+child+1)).key) {
                    child++;
                }
                if (temp.key > (*(heap+child)).key) {
                    break;
                }
                *(heap+parent) = *(heap+child);
                parent = child;
            }
            *(heap+parent) = temp;
        }
    }

/**
 *
 * @param heap  最大堆；
 * @param items 输入的数据源
 * @return 1成功，0失败
 */
int create_binary_tree(element *heap,int items[MAX_ELEMENTS]){
    int total;
    if (!items) {
        return 0;
    }
    element *temp = heap;
    heap++;
    for (total = 1; *items;total++,(heap)++,items = items + 1) {
        element ele = {*items};
        element temp_key = {total};
        *temp = temp_key;
        *heap = ele;
    }
    return 1;
}
///函数调用
int items[MAX_ELEMENTS] = {79,66,43,83,30,87,38,55,91,72,49,9};
element *position = heap;
create_binary_tree(position, items);
for (int i = 0; (*(heap+i)).key > 0; i++) {
  printf("binary tree element is %d\n",(*(heap + i)).key);
}
create_max_heap();
for (int i = 0; (*(heap+i)).key > 0; i++) {
  printf("heap element is %d\n",(*(heap + i)).key);
}

找第k大的元素
建立一个大根堆，做 k−1次删除操作后堆顶元素就是我们要找的答案。

class Solution {
public:
    void maxHeapify(vector<int>& a, int i, int heapSize) {
        int l = i * 2 + 1, r = i * 2 + 2, largest = i;
        if (l < heapSize && a[l] > a[largest]) {
            largest = l;
        } 
        if (r < heapSize && a[r] > a[largest]) {
            largest = r;
        }
        if (largest != i) {
            swap(a[i], a[largest]);
            maxHeapify(a, largest, heapSize);
        }
    }

    void buildMaxHeap(vector<int>& a, int heapSize) {
        for (int i = heapSize / 2; i >= 0; --i) {
            maxHeapify(a, i, heapSize);
        } 
    }

    int findKthLargest(vector<int>& nums, int k) {
        int heapSize = nums.size();
        buildMaxHeap(nums, heapSize);
        for (int i = nums.size() - 1; i >= nums.size() - k + 1; --i) {
            swap(nums[0], nums[i]);
            --heapSize;
            maxHeapify(nums, 0, heapSize);
        }
        return nums[0];
    }
};

小顶堆

二叉搜索树

性质概念

二叉搜索树：一棵二叉树，可以为空；如果不为空，满足以下性质：

1. 非空左子树的所有键值小于其根结点的键值。
2. 非空右子树的所有键值大于其根结点的键值。
3. 左、右子树都是二叉搜索树。

创建 插入 查找

#include<iostream>
using namespace std;

template<class T>
struct Node{
    T val;
    Node* lchild;
    Node* rchild;
};

template<class T>
Node<T>* newNode(int v){
    Node<T>* node = new Node<T>;
    node->val = v;
    node->rchild = node->lchild = nullptr;
    return node;
}

template<class T>
void search(Node<T>* root,int x){
    if(root == nullptr){
        cout<<"Search failed.\n";
        return;
    }
    if(x == root->val){
        cout<<root->val;
    }
    else if(x < root->val){
        search(root->lchild,x);
    }else{
        search(root->rchild,x);
    }
}

template<class T>
void insert(Node<T>* &root,int x){
    if(root == nullptr){
        root = newNode(x);
        return;
    }
    if(x == root->val){
        return;
    }else if(x < root->val){
        insert(root->rchild,x);
    }else{
        insert(root->rchild,x);
    }
}

template<class T>
Node<T>* createBST(T data[],int n){
    Node<T>* root = nullptr;
    for(int i = 0;i < n;i++){
        insert(root,data[i]);
    }
    return root;
}

删除

对于二叉搜索树的删除，考虑以下三种情况：
（1）要删除的是叶结点：直接删除该结点，并把其父节点的指针指向空。
（2）要删除的结点只有一个孩子结点，删除该结点后使该结点的父节点指针指向该结点的子结点。
（3）要删除的结点有左、右两棵子树，则在删除该结点后，需要使该结点的父节点指向被删除结点右子树的最小元素（左下角）或左子树的最大元素（右下角）。

struct TreeNode {
    int val;
    TreeNode* left;
    TreeNode* right;

    TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};

TreeNode* findMin(TreeNode* node) {
    while (node->left != nullptr) {
        node = node->left;
    }
    return node;
}

TreeNode* deleteNode(TreeNode* root, int key) {
    if (root == nullptr) {
        return root;
    }
 
    if (key < root->val) {
        root->left = deleteNode(root->left, key);
    } else if (key > root->val) {
        root->right = deleteNode(root->right, key);
    } else {
        if (root->left == nullptr) {
            TreeNode* temp = root->right;
            delete root;
            return temp;
        } else if (root->right == nullptr) {
            TreeNode* temp = root->left;
            delete root;
            return temp;
        }

        TreeNode* minRight = findMin(root->right);
        root->val = minRight->val;
        root->right = deleteNode(root->right, minRight->val);
    }

    return root;
}

注意：
总是优先删除前驱（or后继）容易导致左右子树的高度极度不平衡，使得二叉查找树退化成一条链

• 每次交替删除前驱或后继
• 记录子树高度，总是优先在高度较高的一侧子树里删除结点

索引二叉搜索树

在二叉搜索树的基础上，给每个节点添加了一个leftSize属性，用于记录该节点左子树的节点个数
基于leftSize属性，搜索树可以按照名次快速找到该名次所对应的节点，从而扩展出了按名次查找节点和删除指定名次的节点的操作。

• 维护好leftsize

#include<iostream>
using namespace std;
template<class T, class E>
struct bsNode//定义索引二叉搜索树节点
{
	pair<T, E> element;//元素为数对，前项表示关键字，后项表示数值
	bsNode<T, E>* leftChild;
	bsNode<T, E>* rightChild;
	int leftSize;//左子树的节点个数
	bsNode(const pair<T, E>& theElement)
	{
		element = theElement;
		leftChild = NULL;
		rightChild = NULL;
		leftSize = 0;
	}
	bsNode(const pair<T, E>& theElement, bsNode<T, E>* LEFT, bsNode<T, E>* RIGHT,int theLeftSize)
	{
		element = theElement;
		leftChild = LEFT;
		rightChild = RIGHT;
		leftSize = theLeftSize;
	}
};

template<class T, class E>
class bsTree
{
public:
	bsTree()
	{
		size = 0;
		root = NULL;
	}
	void ascend() { inOrder(root); }//按关键字顺序输出元素数值
	void find_by_key(const T& theKey)//按关键字查找元素
	{
		bsNode<T, E>* p = root;
		while (p != NULL)
		{
			if (theKey < p->element.first)
				p = p->leftChild;
			else if (theKey > p->element.first)
				p = p->rightChild;
			else
			{
				cout << p->element.second << endl;
				return;
			}

		}
		cout << "Not find" << endl;
	}
	void find_by_index(int& theIndex)//按名次查找元素，输入的名次是从1开始的
	{
		if (theIndex > size)//名次大于元素总个数，无法查找
		{
			cout << "Out of range" << endl;
			return;
		}
		theIndex--;//把名次化为从0开始
		bsNode<T, E>* p = root;
		while (p != NULL&& p->leftSize != theIndex)
		{
			if (theIndex<p->leftSize  )//向左子树走不需要改变theIndex
				p = p->leftChild;
			else//向右子树走需要将theIndex减掉(leftSize+1)
			{
				theIndex = theIndex - 1 - p->leftSize;
				p = p->rightChild;
			}
		}
		//循环结束之后p指向所需名次的节点
		cout << p->element.second << endl;
	}
	void insert(const pair<T, E>& theElement)//插入元素
	{
		//先寻找元素位置，根据关键字判断元素是否已经存在
		bsNode<T, E>* p = root;//用于寻找安放空位
		bsNode<T, E>* pp = NULL;//p节点的父节点
		while (p != NULL)//寻找
		{
			pp = p;
			if (theElement.first < p->element.first)
				p = p->leftChild;
			else if (theElement.first > p->element.first)
				p = p->rightChild;
			else//若已经存在，则退出函数
			{
				cout << "Has existed" << endl;
				return;
			}
		}
		bsNode<T, E>* newNode = new bsNode<T, E>(theElement);
		if (root != NULL)//树非空
		{
			if (theElement.first < pp->element.first)
				pp->leftChild = newNode;
			else
				pp->rightChild = newNode;
		}
		else//树空
			root = newNode;
		size++;
		//修改路径上的leftSize
		bsNode<T, E>* q = root;
		while (q != NULL&&q->element.first!=theElement.first)
		{
			if (theElement.first < q->element.first)//只有当指针向左子树走的时候，根节点的leftSize需要加1
			{
				q->leftSize++;
				q = q->leftChild;
			}
			else if (theElement.first > q->element.first)
			{
				q = q->rightChild;
			}
		}
		
	}
	void erase_by_key(const T& theKey)//按关键字删除元素
	{
		//先确定元素是否存在
		bsNode<T, E>* p = root;//用于寻找需要删除的节点
		bsNode<T, E>* pp = NULL;//p节点的父节点
		while (p != NULL && p->element.first != theKey)//把p定位到删除节点上
		{
			pp = p;
			if (theKey < p->element.first)
				p = p->leftChild;
			else
				p = p->rightChild;
		}
		if (p == NULL)//若p为空，则说明删除节点不存在，退出函数
		{
			cout << "Not exist" << endl;
			return;
		}
		//再次寻找，修改路径上的leftSize
		p = root;//用于寻找需要删除的节点
		pp = NULL;//p节点的父节点
		while (p != NULL && p->element.first != theKey)//把p重新定位到删除节点上
		{
			pp = p;
			if (theKey < p->element.first)
			{
				p->leftSize--;
				p = p->leftChild;
			}
			else
				p = p->rightChild;
		}
		if (p->leftChild != NULL && p->rightChild != NULL)//若删除节点有两个子树，则需要将右子树最大值（或左子树最小值）复制到删除节点上，然后转化为删除右子树最大值（或左子树最小值）节点
		{
			bsNode<T, E>* s = p->rightChild;//寻找p右子树的最小值
			bsNode<T, E>* ps = p;//s节点的父节点
			while (s->leftChild != NULL)//循环结束后，s指向p的右子树的最小值
			{
				s->leftSize--;//寻找右子树最小值的过程中，需要修改路径上的leftSize
				ps = s;
				s = s->leftChild;
			}
			p->element = s->element;
			bsNode<T, E>* q = new bsNode<T, E>(s->element, p->leftChild, p->rightChild,p->leftSize);//q节点的元素是p节点右子树的最小值，q节点的位置是p
			if (pp == NULL)//以q节点替换p节点
				root = q;
			else if (p == pp->leftChild)
				pp->leftChild = q;
			else
				pp->rightChild = q;

			if (ps == p)//把pp移动到s节点的父节点
				pp = q;
			else
				pp = ps;
			delete p;
			p = s;//把p移动到s节点，之后的操作相当于删除s节点
		}
		//之后删除节点至多只有一个子树
		bsNode<T, E>* c;
		if (p->leftChild != NULL)
			c = p->leftChild;
		else
			c = p->rightChild;
		if (p == root)
			root = c;
		else
		{
			if (p == pp->leftChild)
				pp->leftChild = c;
			else
				pp->rightChild = c;
		}
		size--;
		delete p;
	}
	void erase_by_index(int& theIndex)//按名次删除元素（相当于按名次查找和按关键字删除的综合）
	{
		if (theIndex > size)
		{
			cout << "Out of range" << endl;
			return;
		}
		theIndex--;//把名次化为从0开始
		bsNode<T, E>* p = root;//用于寻找需要删除的节点
		bsNode<T, E>* pp = NULL;//p节点的父节点
		while (p != NULL && p->leftSize != theIndex)
		{
			pp = p;
			if (theIndex < p->leftSize)//向左子树走不需要改变theIndex
			{
				p->leftSize--;
				p = p->leftChild;
			}
			else//向右子树走需要将theIndex减掉(leftSize+1)
			{
				theIndex = theIndex - (1 + p->leftSize);
				p = p->rightChild;
			}
		}
		//此时已找到需要删除的元素，剩余代码和按关键字删除相同
		if (p != NULL && p->leftChild != NULL && p->rightChild != NULL)
		{
			bsNode<T, E>* s = p->rightChild;
			bsNode<T, E>* ps = p;
			while (s->leftChild != NULL)
			{
				s->leftSize--;
				ps = s;
				s = s->leftChild;
			}
			p->element = s->element;
			bsNode<T, E>* q = new bsNode<T, E>(s->element, p->leftChild, p->rightChild, p->leftSize);
			if (pp == NULL)
				root = q;
			else if (p == pp->leftChild)
				pp->leftChild = q;
			else
				pp->rightChild = q;

			if (ps == p)
				pp = q;
			else
				pp = ps;
			delete p;
			p = s;
		}
		bsNode<T, E>* c;
		if (p->leftChild != NULL)
			c = p->leftChild;
		else
			c = p->rightChild;
		if (p == root)
			root = c;
		else
		{
			if (p == pp->leftChild)
				pp->leftChild = c;
			else
				pp->rightChild = c;
		}
		size--;
		delete p;
	}
private:
	bsNode<T, E>* root;
	int size;
	void inOrder(bsNode<T, E>* node)//中序遍历
	{
		if (node != nullptr)
		{
			inOrder(node->leftChild);
			cout << node->element.second <<endl;
			inOrder(node->rightChild);
		}
	}
};

选择树

胜者树

1. 是一棵完全二叉树
2. 非叶子节点记录胜者的标号
3. 从建立好的胜者树获取最值的时间代价为O(logn)
4. 胜者树的建立和重构涉及到兄弟节点之间的比较

k 个 leaf node

• the time to initial is O(k)
• the time to reconstruct the tree is O(logk)
• the time to merge all n records is thus O(nlogk)

败者树

1. 是一棵完全二叉树
2. 根节点和它的子节点记录败者的标号->增加一个结点记录比赛的胜者（但参与下轮比赛的仍为胜者）
3. 从建立好的胜者树获取最值的时间代价为O(logn)
4. 败者树的建立和重构仅仅涉及到父子节点之间的比较，即简化了重构的过程

k 个 leaf node

• the time to initialize every inner node the absolute minimal(winner) key is O(k)
• the time to initial a loser tree is O(klogk)
  • if an array is used to store the winner of the tournament, we can set up the loser tree in O(k)

森林

森林转化成二叉树

左孩子右兄弟形式

森林的遍历

先序遍历

• 依次对每棵树进行先序遍历
• 效果等同于先序遍历转化成的二叉树

中序遍历

• 依次对每棵树进行中序遍历
• 效果等同于中序遍历转化成的二叉树

后序遍历

• 依次对每棵树进行后序遍历
• 无自然对应的转换二叉树

层序遍历

• 对森林的每层依次遍历
  • Beginning with the roots of each trees in F
  • Within each level, from left to right.
• 效果不一定等同于层序遍历转化成的二叉树

并查集

Union(合并), Find(查找), Set(集合)

• 合并：合并两个结合
• 查找：判断两个元素是否在一个集合
  对同一个集合来说只存在一个根节点，并将其作为所属集合的唯一标识

Disjoint Sets

• represented with trees, but the nodes are linked from the child to the parent
  

identify sets by the roots of the trees
an array: parent[n]

Union: make one of the trees a subtree of the other
O(1)
void Sets::SimpleUnion(int j,int i){parent[i]=j;}

Find:O(u)
int Sets::SimpleFind(int i){while(parent[i]>=0) i = parent[i]; return i;}

Smart Union Strategies

Height Rule: make tree with smaller height a subtree of the other tree
Weight Rule: make tree with fewer number of elements a subtree of the other tree

int father[N];

int findFather(int x) {
	if (x == father[x])
		return x;
	int z = findFather(father[x]);
	father[x] = z;
	return z;
}

void Union(int a, int b) {
	int faA = findFather(a);
	int faB = findFather(b);
	if (faA != faB) {
		father[faA] = faB;
	}
}

void init(int n) {
	for (int i = 1; i <= n; i++) {
		father[i] = i;
	}
}

AVL树

基本概念

• 二叉查找树
• 任意节点的左子树和右子树的高度差绝对值不超过1
  平衡因子：左子树与右子树的高度之差

基本定义

struct node{
	int v,height;
	node* lchild,*rchild;
};

node* newNode(int v){
	node* Node = new node;
	Node->v = v;
	Node->height = 1;
	Node->lchild = Node->rchild = nullptr;
	return Node;
}

int getHeight(node* root){
	if(root == nullptr) return 0;
	return root->height;
}

int getBalanceFactor(node* root){
	return getHeight(root->lchild) - getHeight(root->rchild);
}

void updateHeight(node* root){
	root->height = max(getHeight(root->lchild), getHeight(root->rchild))+1;
}

基本操作

查找

void search(node* root,int x){
	if(root == nullptr){
		printf("search failed\n");
		return;
	}
	if(x==root->v){
		printf("%d\n",root->v);
	}else if(x < root->v){
		search(root->lchild,x);
	}else{
		search(root->rchild,x);
	}
}

插入

左旋

void L(node* &root){
	node* temp = root->rchild;
	root->rchild = temp->lchild;
	temp->lchild = root;
	updateHeight(root);
	updateHeight(temp);
	root = temp;
}

右旋

void R(node* &root){
	node* temp = root->lchild;
	root->lchild = temp->rchild;
	temp->rchild = root;
	updateHeight(root);
	updateHeight(temp);
	root = temp;
}

处理失衡结点

只要把最靠近插入结点的失衡结点调整到正常，路径上的所有结点就都会平衡

LL型
把以C为根节点的子树看成一个整体，然后以A作为root进行右旋

LR型
先忽略结点A，以结点C为root进行左旋，再按LL型的做法进行右旋

RL/RR型与上面的情况对称

void insert(node *&root, int v) {
	if (root == nullptr) {
		root = newNode(v);
		return;
	}
	if (v < root->v) {
		insert(root->lchild, v);
		updateHeight(root);
		if (getBalanceFactor(root) == 2) {
			if (getBalanceFactor(root->rchild) == 1) {
				R(root);
			} else if (getBalanceFactor(root->rchild) == -1) {
				L(root->lchild);
				R(root);
			}
		}
	} else {
		insert(root->rchild, v);
		updateHeight(root);
		if (getBalanceFactor(root) == -2) {
			if (getBalanceFactor(root->rchild) == -1) {
				L(root);
			} else if (getBalanceFactor(root->rchild) == 1) {
				R(root->lchild);
				L(root);
			}
		}
	}
}

建立

node* create(int data[],int n){
	node* root = nullptr;
	for(int i = 0;i < n;i++){
		insert(root,data[i]);
	}
	return root;
}

删除

普通删除，在AVL树中删除结点值为key的元素（最终得到的树应仍为AVL树）

#include <iostream>
using namespace std;

// AVL鑺傜偣绫?
class AVLNode {
public:
    int key;
    int height;
    AVLNode* left;
    AVLNode* right;
    AVLNode(int k) {
        key = k;
        height = 1;
        left = nullptr;
        right = nullptr;
    }
};


class AVLTree {
private:
    AVLNode* root;

    int getHeight(AVLNode* node) {
        if (node == nullptr)
            return 0;
        else
            return node->height;
    }

    int max(int a, int b) {
        return (a > b) ? a : b;
    }

    void updateHeight(AVLNode* node) {
        node->height = 1 + max(getHeight(node->left), getHeight(node->right));
    }

    int getBalanceFactor(AVLNode* node) {
        if (node == nullptr)
            return 0;
        else
            return getHeight(node->left) - getHeight(node->right);
    }

    AVLNode* leftRotate(AVLNode* node) {
        AVLNode* newRoot = node->right;
        AVLNode* subtree = newRoot->left;
        newRoot->left = node;
        node->right = subtree;
        updateHeight(node);
        updateHeight(newRoot);

        return newRoot;
    }

    AVLNode* rightRotate(AVLNode* node) {
        AVLNode* newRoot = node->left;
        AVLNode* subtree = newRoot->right;
        newRoot->right = node;
        node->left = subtree;
        updateHeight(node);
        updateHeight(newRoot);

        return newRoot;
    }

    AVLNode* balanceNode(AVLNode* node) {
        updateHeight(node);
        int balanceFactor = getBalanceFactor(node);
        if (balanceFactor > 1) {
            if (getBalanceFactor(node->left) >= 0)
                return rightRotate(node);
            if (getBalanceFactor(node->left) < 0) {
                node->left = leftRotate(node->left);
                return rightRotate(node);
            }
        }

        if (balanceFactor < -1) {
            if (getBalanceFactor(node->right) <= 0)
                return leftRotate(node);
            if (getBalanceFactor(node->right) > 0) {
                node->right = rightRotate(node->right);
                return leftRotate(node);
            }
        }
        return node;
    }

    AVLNode* insertNode(AVLNode* node, int key) {
        if (node == nullptr)
            return new AVLNode(key);

        if (key < node->key)
            node->left = insertNode(node->left, key);
        else if (key > node->key)
            node->right = insertNode(node->right, key);
        else
            return node;  
        return balanceNode(node);
    } 

    AVLNode* deleteNode(AVLNode* node, int key) {
        if (node == nullptr)
            return node;
        if (key < node->key)
            node->left = deleteNode(node->left, key);
        else if (key > node->key)
            node->right = deleteNode(node->right, key);
        else {
            if (node->left == nullptr || node->right == nullptr) {
                AVLNode* temp = node->left ? node->left : node->right;

                
                if (temp == nullptr) {
                    temp = node;
                    node = nullptr;
                } else { 
                    *node = *temp;
                }

                delete temp;
            } else {
                AVLNode* temp = findMinNode(node->right);
                node->key = temp->key;
                node->right = deleteNode(node->right, temp->key);
            }
        }
        if (node == nullptr)
            return node;
        return balanceNode(node);
    }

    AVLNode* findMinNode(AVLNode* node) {
        AVLNode* current = node;
        while (current && current->left != nullptr)
            current = current->left;
        return current;
    }

    void inorderTraversal(AVLNode* node) {
        if (node != nullptr) {
            inorderTraversal(node->left);
            cout << node->key << " ";
            inorderTraversal(node->right);
        }
    }

public:
    AVLTree() {
        root = nullptr;
    }

    void insert(int key) {
        root = insertNode(root, key);
    }

   
    void remove(int key) {
        root = deleteNode(root, key);
    }

    void tra()
    {
        inorderTraversal(root);
    }

};

int main() {
    AVLTree avlTree;

    avlTree.insert(10);
    avlTree.insert(20);
    avlTree.insert(30);
    avlTree.insert(40);
    avlTree.insert(50);
    avlTree.insert(25);

    avlTree.tra();
    cout<<"\n";

    avlTree.remove(30);
    
    avlTree.tra();
    return 0;
}

利用lsize，删除第k小的结点

#include<iostream>
using namespace std;

class AVLNode {
public:
    int data;
    int lsize;  
    AVLNode* left;
    AVLNode* right;

    AVLNode(int val) {
        data = val; 
        lsize = 0;
        left = nullptr;
        right = nullptr;
    }
};

class AVLTree {
private:
    AVLNode* root;
    void inorderTraversal(AVLNode* node) {
        if (node != nullptr) {
            inorderTraversal(node->left);
            cout << node->data << " ";
            inorderTraversal(node->right);
        }
    }

    AVLNode* insertNode(AVLNode* node, int val) {
        if (node == nullptr) {
            return new AVLNode(val);
        }
        if (val < node->data) {
            node->lsize++;
            node->left = insertNode(node->left, val);
        } else {
            node->right = insertNode(node->right, val);
        }
        return balance(node);
    }

public:
    AVLTree() {
        root = nullptr;
    }
    
    void tra()
    {
        inorderTraversal(root);
    }
    
	 int getSize(AVLNode* node) {
        if (node == nullptr) {
            return 0;
        }
        return node->lsize + 1 + getSize(node->right);
    }

    void insert(int k){
        root = insertNode(root,k);
    }

    AVLNode* removeKthSmallest(AVLNode* node, int k) {
        if (node == nullptr) {
            return nullptr;
        }
        int leftSize = getSize(node->left);
        if (k <= leftSize) {
            node->lsize--;
            node->left = removeKthSmallest(node->left, k);
        } else if (k > leftSize + 1) {
            node->right = removeKthSmallest(node->right, k - leftSize - 1);
        } else {
            if (node->left == nullptr) {
                AVLNode* temp = node->right;
                delete node;
                return temp;
            } else if (node->right == nullptr) {
                AVLNode* temp = node->left;
                delete node;
                return temp;
            }
            AVLNode* temp = getMinNode(node->right);
            node->data = temp->data;
            node->right = removeKthSmallest(node->right, 1);
        }
        return balance(node);
    }
    
    AVLNode* getMinNode(AVLNode* node) {
        if (node == nullptr)
            return nullptr;
        while (node->left != nullptr)
            node = node->left;
        return node;
    }
    
    AVLNode* getRoot() {
        return root;
    }

private:
    AVLNode* rotateLeft(AVLNode* node) {
        AVLNode* newNode = node->right;
        node->right = newNode->left;
        newNode->left = node;
        return newNode;
    }
   
    AVLNode* rotateRight(AVLNode* node) {
        AVLNode* newNode = node->left;
        node->left = newNode->right;
        newNode->right = node;
        return newNode;
    }

    AVLNode* balance(AVLNode* node) {
        if(node==nullptr) return nullptr;
        int balanceFactor = getHeight(node->left) - getHeight(node->right);
          
        if (balanceFactor > 1) {
            if (getHeight(node->left->left) >= getHeight(node->left->right)) {
                node = rotateRight(node);
            } else {
                node->left = rotateLeft(node->left);
                node = rotateRight(node);
            }
        }

        else if (balanceFactor < -1) {
            if (getHeight(node->right->right) >= getHeight(node->right->left)) {
                node = rotateLeft(node);
            } else {
                node->right = rotateRight(node->right);
                node = rotateLeft(node);
            }
        }

        return node;
    }

    int getHeight(AVLNode* node) {
        if (node == nullptr) {
            return 0;
        }
        return max(getHeight(node->left), getHeight(node->right)) + 1;
    }
};

int main() {
    AVLTree avl;

    
    avl.insert(5);
    avl.insert(3);
    avl.insert(7);
    avl.insert(2);
    avl.insert(4);
    avl.insert(6);
    avl.insert(8);

    avl.tra();
    cout<<"\n";
    
    avl.removeKthSmallest(avl.getRoot(), 3);
    avl.tra();

    return 0;
}

---

设AVL树的高度为H，那么最坏情况下，一个结点的插入和删除各需要多少次调整操作？请说明原因

• 结点插入：最多进行1次调整操作。因为结点插入时AVL树中某个子树的调整，不会影响其父节点的平衡情况
• 结点删除：最多进行H-2次调整操作。因为删除结点时AVL树中某个子树的调整，可能减小该子树的高度，进而影响其父节点的平衡状态

Chap 6 Graph

表示方法

ADT Gragh

![[Pasted image 20231128174636.png|500]]

![[Pasted image 20231128174742.png|500]]

Adjacency Matrix

Using an adjacency matrix representation, we need O(n^2) time to get the number of edges in G.
（n^2-n）entries of the matrix have to be examined 对角线元素均为0

space:n^2
无向图可只存一半（对称矩阵）

time to find vertex degree or vertices adjacent to a given vertex:O(n)

无向图

有向图

typedef char VertexType;
typedef int EdgeType;
#define MAXVEX 100
#define INFINITY 65535 //65535 stands for infinity

typedef struct{
    VertexType vexs[MAXVEX];
    EdgeType arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;
}MGraph;

void createMGraph(MGraph *G){
    int i,j,k,w;
    cout<<"input the number of vertexes and edges:";
    cin>>G->numVertexes>>G->numEdges;
    for(i = 0;i < G->numVertexes;i++)
        cin>>G->vexs[i];
    for(i = 0;i < G->numEdges;i++)
        for(j = 0;j < G->numEdges;j++)
            G->arc[i][j] = INFINITY;
    for(k = 0;k < G->numEdges;k++){
        cin>>i>>j>>w;//edge(vi,vj) and weight
        G->arc[i][j] = w;
        G->arc[j][i] = G->arc[i][j];
    }
}

对稀疏图来说，如果我们单独存下图中的每条边，我们可以用O(e+n)的时间解决问题
This leads to the next representaion.

Adjacency Lists

把数组和链表相结合的存储方法

Linked Adjacency Lists

class LinkedGraph{
public: 
	LinkedGraph(const int vertices):e(0){
		if(vertices < 1) throw"Number of vertices must be > 0";
		n = vertices;
		adjLists = new Chain<int>[n];
	}
private:
	Chain<int>* adjLists;
	int n;
	int e;
};

添加新边

#include<iostream>
#define OK 1
#define ERROR -1
#define MVNum 100
using namespace std;
 
typedef struct VNode{
	int data;
	struct VNode *next;
}VNode,*NodeList;
typedef struct{
	NodeList V[MVNum];
	int vexnum,arcnum;
}ALGraph;
 
int CreateUDG(ALGraph &G,int vexnum,int arcnum){
	G.vexnum = vexnum;
	G.arcnum = arcnum;
	for(int i=1;i<=vexnum; i ++){
		G.V[i] = new VNode;
		G.V[i]->next = NULL;
		G.V[i]->data = i;
	}
	//头插法
    for(int i=0;i<arcnum;i++){
		int v1,v2;
		cin>>v1>>v2;
		NodeList p1 =new VNode;
		p1->data =v2;
		p1->next =G.V[v1]->next;
		G.V[v1]->next = p1;
		NodeList p2 =new VNode;
		p2->data = v1;
		p2->next = G.V[v2]->next;
		G.V[v2]->next = p2;	
	}
	return OK;
}
 
int InsertArc(ALGraph &G){
	int v1,v2;
	cin>>v1>>v2;
	NodeList p1 =new VNode;
	p1->data =v2;
	p1->next =G.V[v1]->next;
	G.V[v1]->next = p1;
	NodeList p2 =new VNode;
	p2->data = v1;
	p2->next = G.V[v2]->next;
	G.V[v2]->next = p2;	
}
 
int PrintAL(ALGraph G){
	for(int i=1;i<=G.vexnum;i++){
		NodeList p =G.V[i];
		while(p->next){
			cout<<p->data<<" ";
			p = p->next;
		}
		cout<<p->data<<endl; 
	}
	return OK;
}
 
int main(){
	
	int vexnum,arcnum;
	while(cin>>vexnum>>arcnum&&vexnum!=0&&arcnum!=0){
		ALGraph G;
		CreateUDG(G,vexnum,arcnum);
		InsertArc(G);
		PrintAL(G);
	}
	return 0;
}

Array Adjacency Lists

Adjacency Multilists

1. In the adjacency lists of an undirected graph, each edge(u,v) is represented by 2 entries, one on the list for u, and the other on the list for v.
2. In some situations, it is necessary to be able to determine the second entry for a particular edge and mark that edge as having been examined.

• m
  • boolean mark
  • indicate whether the edge has been examined
• each edge
  • one node in two lists

class MGraph;
class MGraphEdge{
public:
    MGraphEdge(int u,int v){
        m = false;
        vertex1 = u;
        vertex2 = v;
        link1 = link2 = 0;
    }
private:
    bool m;
    int vertex1, vertex2;
    MGraphEdge *link1,*link2;
};

typedef MGraphEdge * EdgePtr;

class MGraph{
public:
    MGraph(const int vertices):e(0){
        if(vertices<1) throw"Number of vertices must be > 0";
        n = vertices;
        adjMultiLists = new EdgePtr[n];
        fill(adjMultiLists,adjMultiLists+n,(EdgePtr)0);
    }
private:
    EdgePtr* adjMultiLists;
    int n;
    int e;
};

图中的lists为：

1. vertex 0: N0->N1->N2
2. vertex 1: N0->N3->N4
3. vertex 2: N1->N3->N5
4. vertex 3: N2->N4->N5

p 指向 (u,v)边时，已知u可以这样得到v

if(p->vertex1 == u) v = p->vertex2;
else v = p->vertex1;

插入一条边

void MGraph::InsertEdge(int u,int v){
    MGraphEdge *p = new MGraphEdge;
    p->m = false;
    p->vertex1 = u;
    p->vertex2 = v;
    p->link1 = adjMultiLists[u];
    p->link2 = adjMultiLists[v];
    adjMultiLists[u] = adjMultiLists[v] = p;
}

删除一条边

Orthogonal List

十字链表

• 将邻接表和逆邻接表结合起来

重新定义结点结构

• Edge node: m,tail,head,column link,row link
• Vertex node: data, firstin, firstout
  

优点：

• 容易求得顶点的出度和入度
• 虽然结构复杂，但是创建图算法的时间复杂度和邻接表相同

图的基本操作

遍历

深度优先遍历DFS

整体算法思想

• same complexity as BFS
• same properties with respect to path finding, connected components, and spanning trees

不同情况的实现

连通图

bool visited[MVNum];                   //访问标志数组，其初值为“false”
void DFS(Graph G,int v)     
{//从第v个顶点出发递归地深度优先遍历图G             
   cout<<v;visited[v]=true;            //访问第v个顶点，并置访问标志数组相应分量值为true  
   for(w=FirstAdjVex(G,v);w>=0;w=NextAdjVex(G,v,w))   
   //依次检查v的所有邻接点w ，FirstAdjVex(G, v)表示v的第一个邻接点  
   //NextAdjVex(G,v,w)表示v相对于w的下一个邻接点，w≥0表示存在邻接点  
      if(!visited[w]) DFS(G,w);       //对v的尚未访问的邻接顶点w递归调用DFS  
}

非连通图

void DFSTraverse(Graph G)
{//对非连通图G做深度优先遍历
   for(v=0;v<G.vexnum;++v) visited[v]=false;         //访问标志数组初始化
   for(v=0;v<G.vexnum;++v)                           //循环调用针对连通图的算法
   if(!visited[v]) DFS(G,v);                         //对尚未访问的顶点调用DFS
}

对于非连通图的算法，每调用一次连通图算法将遍历一个连通分量，有多少次调用，就说明图中有多少个连通分量。

存储结构为邻接矩阵时

void DFS_AM(AMGraph G,int v)
{//图G为邻接矩阵类型，从第v个顶点出发深度优先搜索遍历图G
   cout<<v;visited[v]=true;      //访问第v个顶点，并置访问标志数组相应分量值为true
   for(w=0;w<G.vexnum;w++)                           //依次检查邻接矩阵v所在的行
     if((G.arcs[v][w]!=0)&&(!visited[w])) DFS(G,w);  
     //G.arcs[v][w]!=0表示w是v的邻接点，如果w未访问，则递归调用DFS
}

存储结构为邻接表时

#include<iostream>
using namespace std;

#define MVNum 100                         //最大顶点数  
typedef struct ArcNode                    //边结点 
{                   
   int adjvex;                           //该边所指向的顶点的位置  
   struct ArcNode * nextarc;             //指向下一条边的指针                        //和边相关的信息  
}ArcNode;  
typedef struct VNode                     //顶点信息 
{  
   int data;    
   ArcNode *firstarc;                   //指向第一条依附该顶点的边的指针  
}VNode,AdjList[MVNum];                  //AdjList表示邻接表类型  
typedef struct                          //邻接表 
{  
    AdjList vertices;                    
    int vexnum,arcnum;                 //图的当前顶点数和边数  
}ALGraph;

int LocateVex(ALGraph& G,int v){
    for(int i = 0;i < G.vexnum;i++){
        if(v==G.vertices[i].data) return i;
    }
    return -1;
}

void CreateUDG(ALGraph &G)
{//采用邻接表表示法，创建无向图G 
    cout<<"Please input the num of vertex and edge:";
    cin>>G.vexnum>>G.arcnum;    //输入总顶点数，总边数 
    int i,j,k;
    int v1,v2;          
    ArcNode *p1,*p2;
    cout<<"\nPlease input the values of vertices:";  
    for(i=0;i<G.vexnum;++i)                //输入各点，构造表头结点表 
    {            
       cin>> G.vertices[i].data;           //输入顶点值  
       G.vertices[i].firstarc=NULL;       //初始化表头结点的指针域为NULL  
    }         //for  
    cout<<"\nPlease input the edges:";  
    for(int k=0;k<G.arcnum;++k)               //输入各边，构造邻接表 
    {            
       cin>>v1>>v2;                       //输入一条边依附的两个顶点  
       i=LocateVex(G,v1); j=LocateVex(G,v2);     
       //确定v1和v2在G中位置，即顶点在G.vertices中的序号  
       p1=new ArcNode;                    //生成一个新的边结点*p1  
       p1->adjvex=j;                     //邻接点序号为j  
       p1->nextarc=G.vertices[i].firstarc; G.vertices[i].firstarc=p1;   
       //将新结点*p1插入顶点vi的边表头部  
       p2=new ArcNode;                   //生成另一个对称的新的边结点*p2  
       p2->adjvex=i;                     //邻接点序号为i  
       p2->nextarc=G.vertices[j].firstarc; G.vertices[j].firstarc=p2;   
       //将新结点*p2插入顶点vj的边表头部  
    }                                    //for  
}

bool visited[MVNum];          

void DFS_AL (ALGraph G,int v)
{//图G为邻接表类型，从第v个顶点出发深度优先搜索遍历图G
   cout<<v;visited[v]=true;               //访问第v个顶点，并置访问标志数组相应分量值为true
   ArcNode* p=G.vertices[v].firstarc;              //p指向v的边链表的第一个边结点
   while(p!=NULL)                         //边结点非空
   {
     int w=p->adjvex;                         //表示w是v的邻接点
     if(!visited[w]) DFS_AL(G,w);         //如果w未访问，则递归调用DFS_AL
     p=p->nextarc;                        //p指向下一个边结点
   }                                      //while
}


int main()
{
    ALGraph Graph;
    CreateUDG(Graph);
    DFS_AL(Graph,0);
    return 0;
}

广度优先遍历BFS

借助队列

整体算法思想

#include<iostream>
#include<queue>
using namespace std;

#define MVNum 100                         
typedef struct ArcNode                    
{                   
   int adjvex;                           //该边所指向的顶点的位置  
   struct ArcNode *nextarc;             //指向下一条边的指针                        //和边相关的信息  
}ArcNode;  
typedef struct VNode                     
{  
   int data;    
   ArcNode *firstarc;                   //指向第一条依附该顶点的边的指针  
}VNode,AdjList[MVNum];                  
typedef struct                          //邻接表 
{  
    AdjList vertices;                    
    int vexnum,arcnum;                  
}ALGraph;

int LocateVex(ALGraph& G,int v){
    for(int i = 0;i < G.vexnum;i++){
        if(v==G.vertices[i].data) return i;
    }
    return -1;
}


void CreateUDG(ALGraph &G)
{
    cout<<"Please input the num of vertex and edge:";
    cin>>G.vexnum>>G.arcnum;    
    int i,j,k;
    int v1,v2;          
    ArcNode *p1,*p2;
    cout<<"\nPlease input the values of vertices:";  
    for(i=0;i<G.vexnum;++i)               
    {            
       cin>> G.vertices[i].data;           
       G.vertices[i].firstarc=NULL;      
    }        
    cout<<"\nPlease input the edges:";  
    for(int k=0;k<G.arcnum;++k)               
    {            
       cin>>v1>>v2;                       
       i=LocateVex(G,v1); j=LocateVex(G,v2);     
       
       p1=new ArcNode;                    
       p1->adjvex=j;                      
       p1->nextarc=G.vertices[i].firstarc; G.vertices[i].firstarc=p1;   
       
       p2=new ArcNode;                   
       p2->adjvex=i;                     
       p2->nextarc=G.vertices[j].firstarc; G.vertices[j].firstarc=p2;   
       
    }                                   
}



bool visited[MVNum];          
queue<int> Q;

void BFS_AL(ALGraph G,int v)
{//按广度优先非递归遍历连通图G  
    cout<<v;visited[v]=true;            //访问第v个顶点，并置访问标志数组相应分量值为true  
    while(!Q.empty()) Q.pop();                      //辅助队列Q初始化，置空          
    Q.push(v);                     //v进队  
    while(!Q.empty())               //队列非空 
    {         
        int u = Q.front();
        Q.pop();//队头元素出队并置为u 
        ArcNode* w = new ArcNode;                   
       //依次检查u的所有邻接点w
        for(w = G.vertices[u].firstarc;w!=nullptr;w = w->nextarc)
           if(!visited[w->adjvex])               
           {                  
             cout<<w->adjvex; visited[w->adjvex]=true;  
             Q.push(w->adjvex);             
           }                            
    }                                   
}


int main()
{
    ALGraph Graph;
    CreateUDG(Graph);
    BFS_AL(Graph,0);
    return 0;
}

时间复杂度

When a vertex is removed from the queue, we examine its adjacent vertices

• O(n) if adjacency martix used
• O(vertex degree) if adjacency lists used

Total Time

• O(mn), where m is the number of vertices in the component that is searched(adjacency matrix)
• O(n + sum of component vertex degrees) = O(n + number of edges in component) ,(adj. lists)

实现细节拆解

Path from Vertex v to Vertex u

• start a breadth-first search at vertex v
• terminate when vertex u is visited or when Q becomes empty
• Time
  • O(n^2) with adj matrix
  • O(n+e) with adj lists (e is number of edges)

---

Is the Graph connceted?

• start a breadth-first search at any vertex of the gragh
• graph is conneted iff all n vertexes get visited
• Time
  • O(n^2) with adj matrix
  • O(n+e) with adj lists (e is number of edges)

---

Conneted Components

• start a breadth-first search at any as yet unvisited vertex of the graph
• newly visited vertices(plus edges between them) define a component
• repeat until all vertixes are visited
• Time
  • O(n^2) with adj matrix
  • O(n+e) with adj lists (e is number of edges)

Spanning Tree

BFS/DFS Spanning Tree

• Time
  • O(n^2) with adj matrix
  • O(n+e) with adj lists (e is number of edges)

Minimum-Cost Spanning Tree

贪心算法

• 需要证明：部分最优->整体最优
  采用最小代价原则来构造，解必须满足以下约束：
• 必须只使用图中的边
• 必须刚好使用n-1条边
• 不可以使用产生环的边

Kruskal’s Algorithm

• 每次添加一条边到T中
• 按cost的非降序选边，且不构成环

伪代码

流程

---

可以用min heap来存边，以简化找权值最小的边的过程

• Initialize: O(e)
• the next edge to be chosen or deleted: O(loge)
• worst case of this process: O(eloge+e)
  If the graph is represented by adj matrix or adj list, its representation should be converted to edges array which is expressed as (u,v,weight)

---

判断新加的点是否会导致形成一个环
本质上是看u，v是否在同一个component

• 并查集
  把每个component存储一个set
  s1 = find(u);
  s2 = find(v);
  if(s1 != s2) union(s1,s2);

#include <vector>
#include <algorithm>
using namespace std;

#define MAXV 1000
#define INF 1e9

struct edge {
	int u, v;
	int cost;
} E[MAXV];

bool cmp(edge a, edge b) {
	return a.cost < b.cost;
}

int father[MAXV];

int findFather(int x) {
	if (x == father[x])
		return x;
	int z = findFather(father[x]);
	father[x] = z;
	return z;
}

int kruskal(int n, int m) {
	//n: num of v       m:num of e
	int ans = 0, numE = 0;
	for (int i = 0; i < n; i++) {
		father[i] = i;
	}
	sort(E, E + m, cmp);
	for (int i = 0; i < m; i++) {
		int faU = findFather(E[i].u);
		int faV = findFather(E[i], v);
		if (faU != faV) {
			father[faU] = faV;
			ans += E[i].cost;
			numE++;
			if (numE == n - 1)
				break;
		}
	}
	if (numE != n - 1)
		return -1;
	else
		return ans;
}

证明

Prim’s Algorithm

想法

• Begin with a tree T that contains an arbitrary single vertex.
• Add a least-cost edge (u,v) to T such that T∪{(u,v)} is kept as a tree. Note that edge (u,v) is such that exactly one of u and v is in T.
• Repeat this edge-addition step until T contains n-1 edges.

实现

#include <vector>
using namespace std;

#define MAXV 1000
#define INF 1e9

struct Node {
	int v, dis;
};

vector<Node> adj[MAXV];

int n;
int d[MAXV];
bool vis[MAXV] = {false};

int prim() {
	fill(d, d + MAXV, INF);
	d[0] = 0;
	int ans = 0;
	for (int i = 0; i < n ; i++) {
		int u = -1, MIN = INF;
		for (int j = 0; j < n; j++) {
			if (vis[j] == false && d[j] < MIN) {
				u = j;
				MIN = d[j];
			}
		}
		if (u == -1)
			return -1;
		vis[u] = true;
		ans += d[u];
		for (int j = 0; j < adj[u].size(); j++) {
			int v = adj[u][j].v;
			if (vis[v] == false && adj[u][j].dis < d[v]) {
				d[v] = G[u][v];
			}
		}
	}
	return ans;
}

时间复杂度：
普里姆算法的时间复杂度为O(n2)，与网中的边数无关，因此适用于求稠密网的最小生成树。

Shortest Path

Dijkstra

解决问题

单源最短路径：给定图G和起点s，通过算法得到s到达其他每个顶点的最短距离
适用场景：边权为非负值

基本思想

对图G(V,E)设置集合S，存放已被访问的结点，每次从V-S中选择与起点s的最短距离最小的一个顶点(
记为u)，访问并加入集合S。之后，令顶点u为中介点，优化起点s与所有从u到达的顶点v之间的最短距离。这样的操作执行n次（顶点个数），直到集合S已经包含所有顶点。

图示流程

伪代码

邻接表写法

• 求最短距离
• 求最短路路径
  • pre【】

#include <vector>
using namespace std;

#define MAXV 1000
#define INF 1e9

struct Node {
	int v, dis;
};

vector<Node> adj[MAXV];
int n;
int d[MAXV];
int pre[MAXV];
bool vis[MAXV] = {false};

void dijkstra(int s) {
	fill(d, d + MAXV, INF);
	d[s] = 0;
	for (int i = 0;i < n;i++) pre[i] = i;
	for (int i = 0; i < n; i++) {
		int u = -1, MIN = INF;
		for(int j = 0;j < n;j++){
			if(vis[j]==false && d[j]<MIN){
				u = j;
				MIN = d[j];
			}
		}
		if(u==-1) return;
		vis[u] = true;
		for(int j = 0;j < adj[u].size();j++){
			int v = adj[u][j].v;
			if(vis[v]==false && d[u]+adj[u][j].dis< d[v]){
				d[v] = d[u] + adj[u][j].dis;
				pre[v] = u;
			}
		}
	}
}

void DFS(int s,int v){
	if(v==s){
		printf("%d\n",s);
		return;
	}
	DFS(s,pre[v]);
	printf("%d\n",v);
}

复杂度

O(V^2+E)
如果用堆优化，那么O(VlogV+E)

变式

新增边权

用cost[u][v]代表u->v的花费
新增一个数组c,令从起点s到顶点u的最小花费为c[u]

for(int v = 0;v < n;v++){
	if(vis[v]==false && G[u][v]!=INF){
		if(d[u]+G[u][v] < d[v]){
			d[v] = d[u] + G[u][v];
			c[v] = c[u] + cost[u][v];
		}
		else if(d[u]+G[u][v]==d[v] && c[v]>c[u]+cost[u][v]){
			c[v] = c[u] + cost[u][v];
		}
	}
}

新增点权

用weight[u]代表城市u中的物资数目
新增一个数组w，令起点s到顶点u可以收集到的最大物资为w[u]

for(int v = 0;v < n;v++){
	if(vis[v]==false && G[u][v]!=INF){
		if(d[u]+G[u][v] < d[v]){
			d[v] = d[u] + G[u][v];
			w[v] = w[u] + weight[v];
		}
		else if(d[u]+G[u][v]==d[v] && w[v]<w[u]+weight[v]){
			w[v] = w[u] + weight[v];
		}
	}
}

问最短路径条数

增加一个数组num，令起点s到顶点u的最短路径条数为num[u]
初始化时，nums[s]=1，其余num[u]均为0

for(int v = 0;v < n;v++){
	if(vis[v]==false && G[u][v]!=INF){
		if(d[u]+G[u][v] < d[v]){
			d[v] = d[u] + G[u][v];
			num[v] = num[u];
		}
		else if(d[u]+G[u][v]==d[v]){
			num[v] += num[u];
		}
	}
}

Bellman-Ford算法

解决问题

单源最短路径：给定图G和起点s，通过算法得到s到达其他每个顶点的最短距离
适用场景：边权有负值

基本思想

根据环中边权之和的正负，将环分为零环、正环、负环
算法返回一个bool值

• 存在从源点可达的负环，返回false
• 否则返回true，此时数组d中存放的值就是从源点到达各顶点的最短距离

伪代码

时间复杂度：O(VE)

邻接表写法

#include <vector>
using namespace std;

#define MAXV 1000
#define INF 1e9

struct Node {
	int v, dis;
};

vector<Node> adj[MAXV];

int n;
int d[MAXV];

bool Bellman(int s) {
	fill(d, d + MAXV, INF);
	d[s] = 0;
	for (int i = 0; i < n - 1; i++) {
		for (int u = 0; u < n; u++) {
			for (int j = 0; j < adj[u].size(); j++) {
				int v = adj[u][j].v;
				int dis = adj[u][j].dis;
				if(d[u]+dis < d[v]){
					d[v] = d[u] + dis;
				}
			}
		}
	}
	
	for(int u = 0;u < n;u++){
		for(int j = 0;j < adj[u].size();j++){
			int v = adj[u][j].v;
			int dis = adj[u][j].dis;
			if(d[u]+dis < d[v]){
				return false;
			}
		}
	}
	return true;
}

注意点

求解最短路径、有多重标尺时做法均与Dijkstra相同

但统计最短路径条数时方法会不同:

• BF算法会多次访问曾经访问过的节点
• 应设计记录前驱的数组set<int>pre[MAXV]，当遇到一条和已有最短路径长度相同的路径时，必须重新计算最短路径的条数

SPFA算法

由Bellman-Ford算法优化而来

Bellman-Ford算法不足：每轮操作都需要操作所有边，显然这其中会有大量无意义的操作，严重影响了算法的性能

而：只有当某个顶点u的d[u]改变时，从它出发的临界点v的d[v]值才可能改变

优化：建立一个队列，每次将队首顶点u取出，然后对u出发的所有边u->v进行松弛操作，直至队列为空或某个顶点的入队次数超过V-1

#include <vector>
#include <queue>
#include <cstring>
using namespace std;

#define MAXV 1000
#define INF 1e9

struct Node {
	int v, dis;
};

vector<Node> adj[MAXV];
int n, d[MAXV], num[MAXV];
bool inq[MAXV];

bool SPFA(int s) {
	memset(inq, false, sizeof(inq));
	memset(num, 0, sizeof(num));
	fill(d, d + MAXV, INF);

	queue<int> q;
	q.push(s);
	inq[s] = true;
	num[s]++;
	d[s] = 0;
	while (!q.empty()) {
		int u = q.front();
		q.pop();
		inq[u] = false;
		for (int j = 0; j < adj[u].size(); j++) {
			int v = adj[u][j].v;
			int dis = adj[u][j].dis;

			if (d[u] + dis < d[v]) {
				d[v] = d[u] + dis;
				if (!inq[v]) {
					q.push(v);
					inq[v] = true;
					num[v]++;
					if (num[v] >= n)
						return false;
				}
			}
		}
	}
	return true;
}

如果实现知道图中不会有环，那么num数组部分可以去掉。
注意：使用SPFA可以判断是否存在从源点可达的负环，如果负环从源点不可达，则需要添加一个辅助顶点C，并添加一条从源点到达C的有向边以及V-1条从C到达除源点外各顶点的有向边才能判断负环是否存在

Floyd算法

解决问题

全源最短路径：给定G(V,E)，求任意两点之间的最短路径长度
时间复杂度：O(n^3)

#define MAXV 200
#define INF 1e9

struct Node {
	int v, dis;
};

int n,m;
int dis[MAXV][MAXV];

void Floyd(){
	for(int k = 0;k < n;k++){
		for(int i = 0;i < n;i++){
			for(int j = 0;j < n;j++){
				if(dis[i][k]!=INF && dis[k][j]!=INF && dis[i][k]+dis[k][j] < dis[i][j]){
					dis[i][j] = dis[i][k] + dis[k][j];
				}
			}
		}
	}
}

拓扑排序

概念

将有向无环图G的所有顶点排成一个线性序列，使得对图G中的任意两个顶点u、v，如果存在边u->v，那么在序列中u一定在v前面。

方法步骤

1. 定义一个队列Q，并把所有入度为0的结点加入队列
2. 取队首结点，输出。然后删去所有从它出发的边，并令这些边到达的顶点的入度减去1。如果某个顶点的入度变为0，那么将其加入队列。
3. 反复进行2直至队列为空。如果队列为空时，入过队的结点数目为N，说明拓扑排序成功，图为有向无环图。否则，拓扑排序失败，图G中有环。

代码实现

#include <vector>
#include <queue>
using namespace std;

#define MAXV 1000

vector<int> G[MAXV];

int n, m, inDegree[MAXV];

bool topologicalSort() {
	int num = 0;
	queue<int> q;
	for (int i = 0; i < n; i++) {
		if (inDegree[i] == 0) {
			q.push(i);
		}
	}
	while (!q.empty()) {
		int u = q.front();
		//printf("%d\n",u);
		q.pop();
		for (int i = 0; i < G[u].size(); i++) {
			int v = G[u][i];
			inDegree[v]--;
			if (inDegree[v] == 0) {
				q.push(v);
			}
		}
		G[u].clear();
		num++;
	}
	if (num == n)
		return true;
	else
		return false;
}

如果要求有多个入度为0的顶点，选择编号最小的结点的话，可以把queue改为priority_queue，并保持队首元素是优先队列中最小的元素即可（set也可用）

关键路径

AOV网和AOE网

Activity On Vertex：用顶点表示活动，边集表示活动间优先关系的有向图
Activity On Edge：用带权的边集表示活动，用定点表示事件的有向图
关键路径：AOE网中的最长路径

最长路径

对一个没有正环的图（指从源点可达的正环），可把所有边权*-1变成相反数，然后用Bellman-Ford或SPFA算法求最短路径，最后将结果取反即可。

有向无环图中最长路径

求解有向无环图中最长路径的办法

用数组e和l，其中e[r]、l[r]分别代表活动a_r的最早开始时间和最迟开始时间。通过两者是否相等来确定r是否为关键活动。

事件v_i通过活动a_r到达事件v_j
用数组ve和vl，其中ve[i]和vl[i]分别表示事件i的最早发生时间和最迟发生时间

• 对活动a来说，只要在事件最早发生时马上开始，就可以使得活动开始的事件最早`e[r] = ve[i]
• 活动最迟发生时间和事件最迟发生事件的关系 l[r] = vl[j] - length[r]

按拓扑序列计算，在拓扑排序访问的某个结点Vi时，不是让它去找前驱结点更新ve[i]，而是使用ve[i]来更新其后继结点的ve值。

Chap7 Sorting

插入排序

基本思想

将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

程序代码

void insertion_sort(int arr[], int len) {
	for (int i = 1; i < len; i++) {
		int key = arr[i];
		int j = i - 1;
		while ((j >= 0) && (key < arr[j])) {
			arr[j + 1] = arr[j];
			j--;
		}
		arr[j + 1] = key;
	}
}

快速排序

基本思想

1. 从数列中挑出一个元素，称为 “基准”（pivot）;
2. 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；
3. 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

程序代码

int partition1(int A[], int low, int high) {
	int pivot = A[low];
	while (low < high) {
		while (low < high && A[high] > pivot) {
			--high;
		}
		A[low] = A[high];
		while (low < high && A[low] <= pivot) {
			++low;
		}
		A[high] = A[low];
	}
	A[low] = pivot;
	return low;
}

void quick_sort(int A[], int low, int high) {
	if (low < high) {
		int pivot = partition1(A, low, high);
		quick_sort(A, low, pivot - 1);
		quick_sort(A, pivot + 1, high);
	}
}

（和书上的方法由区别）

归并排序

基本思想

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列；
2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置；
3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置；
4. 重复步骤 3 直到某一指针达到序列尾；
5. 将另一序列剩下的所有元素直接复制到合并序列尾。

程序代码

void merge_sort(int arr[], int len) {
	int *a = arr;
	int *b = new int[len];
	for (int i = 1; i < len; i += i) {
		for (int begin = 0; begin < len; begin += 2 * i) {
			int low = begin;
			int mid = min(begin + i, len);
			int high = min(begin + 2 * i, len);
			int k = low;
			int begin1 = low, end1 = mid;
			int begin2 = mid, end2 = high;
			while (begin1 < end1 && begin2 < end2) {
				b[k++] = a[begin1] < a[begin2] ? a[begin1++] : a[begin2++];
			}
			while (begin1 < end1) {
				b[k++] = a[begin1++];
			}
			while (begin2 < end2) {
				b[k++] = a[begin2++];
			}
		}
		int *temp = a;
		a = b;
		b = temp;
	}
	if (a != arr) {
		for (int i = 0; i < len; i++)
			b[i] = a[i];
		b = a;
	}
	delete[] b;
}

堆排序

基本思想

1. 创建一个堆 H[0……n-1]；
2. 把堆首（最大值）和堆尾互换；
3. 把堆的尺寸缩小 1，并把新的数组顶端数据调整到相应位置；
4. 重复步骤 2，直到堆的尺寸为 1。

程序代码

void max_heapify(int arr[], int start, int end) {
	int dad = start;
	int son = dad * 2 + 1;
	while (son <= end) {
		if (son + 1 <= end && arr[son] < arr[son + 1])
			son++;
		if (arr[dad] > arr[son])
			return;
		else {
			swap(arr[dad], arr[son]);
			dad = son;
			son = dad * 2 + 1;
		}
	}
}

void heap_sort(int arr[], int len) {
	for (int i = len / 2 - 1; i >= 0; i--)
		max_heapify(arr, i, len - 1);
	for (int i = len - 1; i > 0; i--) {
		swap(arr[0], arr[i]);
		max_heapify(arr, 0, i - 1);
	}
}

冒泡排序

基本思想

比较相邻的元素。如果第一个比第二个大，就交换他们两个。
对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。
针对所有的元素重复以上的步骤，除了最后一个。
持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

程序代码

template<typename T> 
void bubble_sort(T arr[], int len) {
        int i, j;
        for (i = 0; i < len - 1; i++)
                for (j = 0; j < len - 1 - i; j++)
                        if (arr[j] > arr[j + 1])
                                swap(arr[j], arr[j + 1]);
}

选择排序

基本思想

首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。
重复第二步，直到所有元素均排序完毕。

程序代码

template<typename T> 
void selection_sort(std::vector<T>& arr) {
        for (int i = 0; i < arr.size() - 1; i++) {
                int min = i;
                for (int j = i + 1; j < arr.size(); j++)
                        if (arr[j] < arr[min])
                                min = j;
                std::swap(arr[i], arr[min]);
        }
}

希尔排序

基本思想

是对插入排序的高效改进版本，先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录"基本有序"时，再对全体记录进行依次直接插入排序。

选择一个增量序列 t1，t2，……，tk，其中 ti > tj, tk = 1；
按增量序列个数 k，对序列进行 k 趟排序；
每趟排序，根据对应的增量 ti，将待排序列分割成若干长度为 m 的子序列，分别对各子表进行直接插入排序。仅增量因子为 1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

程序代码

template<typename T>
void shell_sort(T array[], int length) {
    int h = 1;
    while (h < length / 3) {
        h = 3 * h + 1;
    }
    while (h >= 1) {
        for (int i = h; i < length; i++) {
            for (int j = i; j >= h && array[j] < array[j - h]; j -= h) {
                std::swap(array[j], array[j - h]);
            }
        }
        h = h / 3;
    }
}

非稳定排序算法

外部排序

归并排序法

Chap 8 Hashing

线性探测法删除元素

#include <iostream>
#include <vector>
using namespace std;

class LinearProbingHash {
	private:
		vector<int> table;
		int capacity;
		int size;

	public:
		LinearProbingHash(int capacity) {
			this->capacity = capacity;
			this->size = 0;
			table.resize(capacity, -1);
		}

		int hashFunction(int key) {
			return key % capacity;
		}

		void insert(int key) {
			if (size == capacity) {
				cout << "Hash table is full. Unable to insert." << endl;
				return;
			}

			int index = hashFunction(key);
			while (table[index] != -1 && table[index] != -2) {
				index = (index + 1) % capacity;
			}
			table[index] = key;
			size++;
		}

		void remove(int key) {
			int index = hashFunction(key);
			while (table[index] != -1) {
				if (table[index] == key) {
					table[index] = -2; // Marking the cell as deleted
					size--;
					return;
				}
				index = (index + 1) % capacity;
			}
			cout << "Key not found. Unable to remove." << endl;
		}

		bool search(int key) {
			int index = hashFunction(key);
			while (table[index] != -1) {
				if (table[index] == key) {
					return true;
				}
				index = (index + 1) % capacity;
			}
			return false;
		}

		void print() {
			for (int i = 0; i < capacity; i++) {
				if (table[i] != -1 && table[i] != -2) {
					cout << "Index: " << i << ", Key: " << table[i] << endl;
				}
			}
		}
};

int main() {
	LinearProbingHash hashTable(10);

	hashTable.insert(5);
	hashTable.insert(25);
	hashTable.insert(15);
	hashTable.insert(35);

	cout << "HashTable after insertions:" << endl;
	hashTable.print();

	hashTable.remove(25);
	cout << "HashTable after removing 25:" << endl;
	hashTable.print();

	cout << "Search 15: " << (hashTable.search(15) ? "Found" : "Not found") << endl;
	cout << "Search 25: " << (hashTable.search(25) ? "Found" : "Not found") << endl;
	cout << "Search 35: " << (hashTable.search(35) ? "Found" : "Not found") << endl;

	hashTable.insert(6);
	cout << "HashTable after insertions:" << endl;
	hashTable.print();

	cout << "Search 6: " << (hashTable.search(6) ? "Found" : "Not found") << endl;
	cout << "Search 15: " << (hashTable.search(15) ? "Found" : "Not found") << endl;

	return 0;
}

参考：
教材
算法笔记
菜鸟教程