线性表是一种数据结构,由零个或多个相同数据类型的元素组成的有限序列。这些元素之间存在一定的顺序关系,即每个元素都有一个直接前驱和一个直接后继,除了第一个和最后一个元素外。线性表的特点包括有穷性、一致性和序列性,即元素数量有限、类型一致且有序排列。
线性表的实现方式主要有两种:顺序存储和链式存储。
1:顺序存储:使用数组来存储线性表中的元素,元素在内存中是连续存放的。这种方式的优点是查找效率高,但插入和删除操作可能需要移动大量元素,导致效率较低。

2:链式存储: 通过节点连接的方式实现,每个节点包含数据部分和指向下一个节点的指针。这种方式的优点是插入和删除操作较为方便,但查找效率较低,且存储密度不如顺序存储。
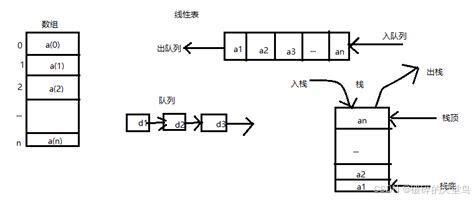
此外,链式存储还可以进一步细分为单链表、双向链表和循环链表等不同形式,每种形式都有其特定的应用场景。
线性表的顺序存储和链式存储在实际应用中的优缺点比较是什么?
线性表的顺序存储和链式存储在实际应用中的优缺点可以从多个方面进行比较。
顺序存储结构(顺序表)
优点:
- 存储密度高:顺序表的存储密度为1,即每个存储单元只存储一个元素,没有额外的空间浪费。
- 随机访问:顺序表可以通过计算地址直接访问任何数据元素,因此具有很高的随机访问效率。
- 简单易用:实现简单,适合存储静态数据,不需要频繁的插入和删除操作。
缺点:
- 插入和删除效率低:插入和删除操作需要移动大量其他元素,效率较低。
- 存储空间固定:顺序表的存储空间是静态分配的,难以动态扩充,当线性表长度变化较大时,容易造成空间浪费或需要频繁扩充。
- 不便于动态变化:顺序表不适合频繁进行插入和删除操作的场景,因为这些操作会导致大量元素的移动。
链式存储结构(链表)
优点:
- 动态分配:链表无需事先估计存储规模,可以动态申请内存空间,适合长度经常波动或事先无法确定长度的线性表。
- 插入和删除灵活:插入和删除操作只需修改指针即可完成,不需要移动其他元素,因此效率较高。
- 存储空间利用率低:链表的存储密度小于1,每个节点除了存储自身信息外,还需要存储指针域,这增加了额外的存储开销。
缺点:
- 随机访问困难:链表中的结点需顺序存取,不能像顺序表那样通过计算地址直接访问,因此随机访问效率较低。
- 指针开销大:每个节点需要额外的指针域来存储关联信息,增加了内存占用。
- 不便于实现:链表的操作基于指针,实现相对复杂,需要更多的编程技巧。
总结
选择顺序存储还是链式存储结构主要取决于具体的应用场景:
- 如果线性表的长度固定且变化不大,且主要操作是查找,则顺序存储结构更为合适。
- 如果线性表的长度经常变化或事先无法确定长度,并且需要频繁进行插入和删除操作,则链式存储结构更为适合。
如何优化线性表的插入和删除操作以提高效率?
为了优化线性表的插入和删除操作以提高效率,可以考虑以下几种方法:
在顺序表中进行插入和删除操作时,通常需要移动大量元素,这导致时间复杂度为O(n)。而链表中的插入和删除操作只需修改指针,不需要移动数据元素,因此更适合频繁的插入和删除操作。
如果插入和删除主要发生在表的首尾两端,可以使用尾指针表示的单循环链表。这种方法在插入和删除操作时只需修改尾指针,从而提高效率。
对于顺序表,当插入操作导致空间不足时,可以通过增加空间来避免频繁的重新分配操作。例如,当线性表的长度达到最大容量的一定比例时,可以将空间扩展一倍,这样可以减少因空间不足而导致的重新分配次数。
在顺序表中插入元素时,尽量选择靠近表尾的位置进行插入,这样可以减少需要移动的元素数量。例如,如果插入位置i为n+1,则无需移动任何元素,时间复杂度为O(1),这是最好的情况。
如果顺序表中的元素按照值的升序或降序排列,可以使用二分查找法来定位插入位置,从而将时间复杂度从O(n)降低到O(log n)。这种方法特别适用于查找频繁但插入和删除较少的情况。
在单片机中实现动态线性表时,可以通过定义变量和程序流程来简化插入操作。例如,通过设置起始地址、偏移量、最大长度等变量,并在插入时检查是否达到表格最大长度,从而实现快速插入。
单链表、双向链表和循环链表的具体应用场景有哪些?
单链表、双向链表和循环链表在不同的应用场景中具有各自的优势和特点。以下是它们的具体应用场景:
单链表
单链表是一种基本的链表结构,每个节点包含数据部分和指向下一个节点的指针。由于其结构简单,单链表通常用于以下场景:
- 栈(Stack) :单链表可以高效地实现栈结构,因为插入和删除操作都在链表的一端进行,表现出先进后出(LIFO)的特性。
- 队列(Queue) :当插入操作在链表的一端进行,删除操作在另一端进行时,单链表表现出先进先出(FIFO)的特性,适用于队列的实现。
- 哈希表(Hash Table) :在解决哈希冲突时,冲突的元素会被放到一个链表中,单链表可以作为哈希表的辅助数据结构。
- 图(Graph) :邻接表是表示图的一种常用方式,其中每个顶点都与一个链表相关联,链表中的每个元素代表与该顶点相连的其他顶点。
- 操作系统中的进程管理:单链表可以用于分配和回收进程的存储空间。
双向链表
双向链表的每个节点不仅包含指向下一个节点的指针,还包含指向前一个节点的指针。这种结构使得双向链表在需要快速查找前一个和后一个元素的场景中非常有用:
- 双向队列(Deque) :双向链表允许在队列的两端进行插入和删除操作,提高了队列的效率。
- 高级数据结构:例如红黑树和B树中,需要访问节点的父节点,这可以通过在节点中保存一个指向父节点的引用来实现,类似于双向链表。
- 符号表(Symbol Table) :在编译器构建中,符号表可以使用双向链表来实现,以便快速查找和更新符号信息。
循环链表
循环链表的特点是最后一个节点指向第一个节点,形成一个闭环。这种结构适用于需要循环访问元素的场景:
- 轮询调度器(Round Robin Scheduler) :循环链表允许元素按顺序访问,适用于轮询调度器的应用场景。
- 邮件列表:循环链表可以用于邮件列表管理,以便顺序打印或处理邮件。
- 图形用户界面中的滚动列表:循环链表可以用于实现滚动列表,用户可以通过滚动条查看列表中的所有元素。
总结来说,单链表、双向链表和循环链表各有其独特的应用场景和优势。
线性表在大数据处理中的表现如何,与其他数据结构相比有何优势和劣势?
线性表在大数据处理中的表现取决于其存储方式,即顺序存储结构和链式存储结构。每种存储方式都有其优势和劣势。
顺序存储结构(顺序表)
优点:
- 存储密度高:不需要额外的存储空间来表示元素之间的逻辑关系,因此空间利用率高。
- 随机存取:可以通过下标直接访问任意位置的元素,时间复杂度为O(1),非常高效。
- 适用于固定长度的线性表:如果事先知道线性表的大致长度,如一年12个月或一周7天,顺序存储结构的效率会更高。
缺点:
- 插入和删除效率低:插入或删除一个元素时,可能需要移动大量其他元素,特别是在表的一端进行操作时,效率较低。
- 空间浪费:顺序存储结构属于静态存储形式,数据元素个数不能自由扩充,初始空间大小分配难以掌握,可能导致空间浪费。
- 不便于动态调整:由于顺序表需要预先分配固定大小的存储空间,因此在数据量变化较大时,不适合使用顺序存储结构。
链式存储结构(链表)
优点:
- 动态分配:链表的存储空间是动态分配的,可以根据需要随时增加或减少存储单元,非常适合处理长度变化较大的线性表。
- 插入和删除高效:插入和删除操作只需修改指针,不需要移动其他元素,因此效率较高。
- 灵活性高:链表中的元素可以任意存放,可以通过修改指针的方式灵活地修改表的结构。
缺点:
- 随机存取困难:链表不支持随机存取,只能通过头指针从头开始逐个访问元素,时间复杂度为O(n),效率较低。
- 额外开销:每个节点需要额外的存储空间来保存指针信息,增加了存储开销。
- 不适用于频繁检索:链表不适合需要频繁进行顺序检索或二分检索的应用场景,因为这些操作需要遍历整个链表或进行排序。
总结
在大数据处理中,选择合适的线性表存储方式至关重要。顺序存储结构适用于长度固定且不需要频繁插入和删除操作的场景,而链式存储结构则更适合处理长度变化较大且需要频繁插入和删除操作的数据集。
线性表的高级操作(如排序、搜索)在不同实现方式下的效率对比是怎样的?
线性表的高级操作,如排序和搜索,在不同实现方式下的效率对比可以从多个角度进行分析。
对于排序操作,顺序表和链表是两种常见的实现方式。顺序表通过将元素顺序存放在一大块连续的存储区里,可以利用计算机内存的特点来提高操作效率。然而,顺序表在插入和删除操作时需要移动大量元素,导致时间复杂度较高。相比之下,链表通过链接构造起来的一系列存储块,可以在插入和删除操作时避免移动大量元素,但其查找操作的时间复杂度较高。
在搜索操作方面,顺序查找和二分查找是两种主要的算法。顺序查找适用于顺序表和链表,但效率较低,时间复杂度为O(n),即随着数据量的增加,搜索时间成线性增长。二分查找则适用于已排序的列表,通过将列表分为两半并逐步缩小搜索范围,显著提高了查找速度,时间复杂度为O(logn),增长速度远慢于线性搜索。
此外,基于线性表的频繁项集挖掘算法在处理稀疏数据集时,尤其是低支持度设置下,展现出更快的挖掘速度,优于位组合算法和FP-growth算法。这表明在特定应用场景下,线性表的实现方式可以提供更高的效率。
线性表的高级操作在不同实现方式下的效率对比取决于具体的应用场景和数据特性。顺序表和链表在存储密度和空间效率方面存在差异,而顺序查找和二分查找在查找效率上也有显著区别。

























 3635
3635

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










