(1)Python所有方向的学习路线(新版)
这是我花了几天的时间去把Python所有方向的技术点做的整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照上面的知识点去找对应的学习资源,保证自己学得较为全面。
最近我才对这些路线做了一下新的更新,知识体系更全面了。

(2)Python学习视频
包含了Python入门、爬虫、数据分析和web开发的学习视频,总共100多个,虽然没有那么全面,但是对于入门来说是没问题的,学完这些之后,你可以按照我上面的学习路线去网上找其他的知识资源进行进阶。
(3)100多个练手项目
我们在看视频学习的时候,不能光动眼动脑不动手,比较科学的学习方法是在理解之后运用它们,这时候练手项目就很适合了,只是里面的项目比较多,水平也是参差不齐,大家可以挑自己能做的项目去练练。

网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。
一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!
if node.right:
new_list.append(node.right)
layers = new_list
return height
# 二叉树可视化
def visualize(self, axis='off'):
'''
基本算法: 将树状结构映射到二维矩阵中,
如果节点左右下方有节点则把该节点加入到矩阵中的坐标中,
如节点(x,y)左下方有节点则把节点放入(x+offset,y+1)
offset为x坐标偏移量,
offset = 2**(len(matrix)-y-2)
'''
figure, axes = plt.subplots(figsize=(8, 6), dpi=80)
height = self.get_height()
width_ = 2 ** (height - 1)
width = 2 * width_ + 1
matrix = [[[] for x in range(width)] for y in range(height)]
matrix[0][width_] = bst_tree # put head in the middle position
for y in range(len(matrix)):
for x in range(len(matrix[y])):
node = matrix[y][x]
if node:
x1, y1 = (1 / width) * (x + 0.32), 1 - (1 / height) * y - 0.21
axes.text(x1, y1, str(node.value), color='white', fontsize=FONT_SIZE, fontweight='bold')
offset = 2 ** (len(matrix) - y - 2)
if node.left:
matrix[y + 1][x - offset] = node.left
x2, y2 = (1 / width) * (x - offset + 0.5), 1 - (1 / height) * (y + 1) - 0.2
line = mlines.Line2D([x1, x2], [y1, y2], zorder=-1)
axes.add_line(line)
if node.right:
matrix[y + 1][x + offset] = node.right
x2, y2 = (1 / width) * (x + offset + 0.5), 1 - (1 / height) * (y + 1) - 0.2
line = mlines.Line2D([x1, x2], [y1, y2], zorder=-1)
axes.add_line(line)
cc = plt.Circle(((1 / width) * (x + 0.5), 1 - (1 / height) * y - 0.2), 1 / width / 2 * NODE_SIZE_SCALE, color='blue')
axes.set_aspect(1)
axes.add_artist(cc)
plt.axis(axis)
plt.show()
使用递归的方式构建二叉搜索树
def make_binary_search_tree(data):
if not data:
return
data.sort()
mid = len(data) // 2
tree = Node(data[mid], # 中间节点数据
make_binary_search_tree(data[:mid]), # 左子树
make_binary_search_tree(data[mid+1:])) # 右子树
return tree
FONT_SIZE = 20
NODE_SIZE_SCALE = 1
X = [3, 6, 5, 2, 4, 1, 7]
if name == ‘main’:
bst = make_binary_search_tree(X)
bst.visualize()
运行结果:
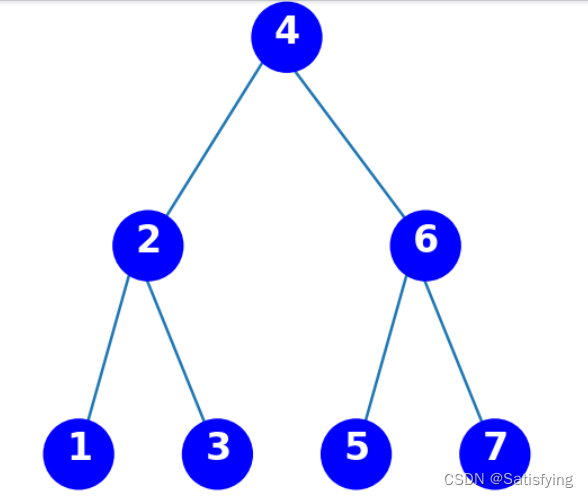
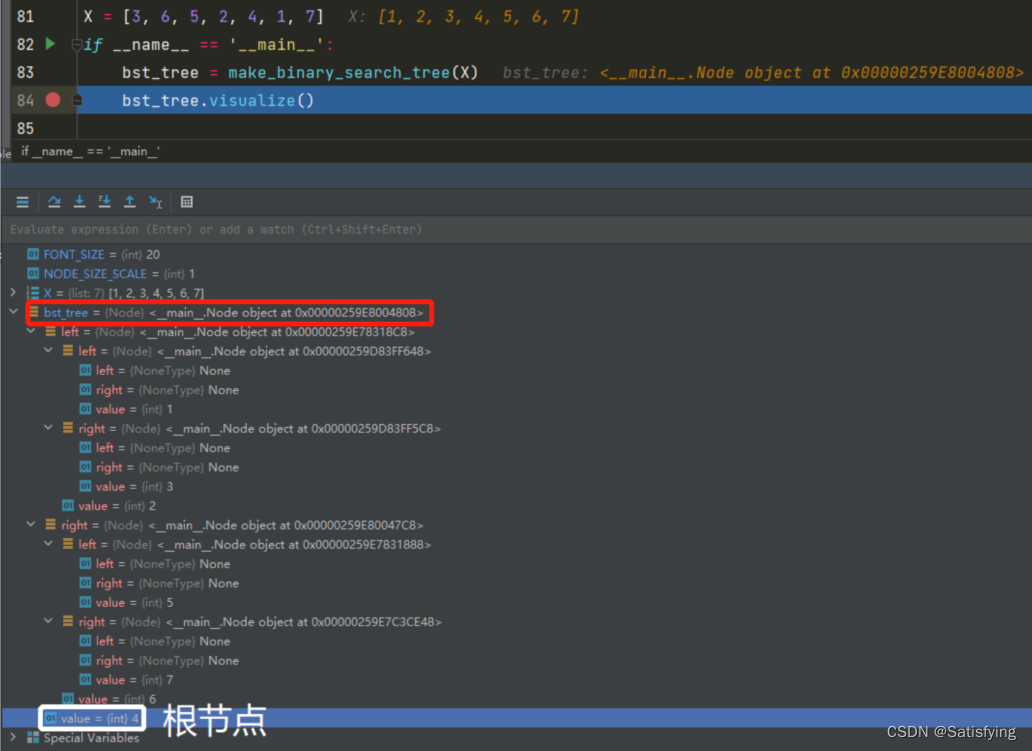
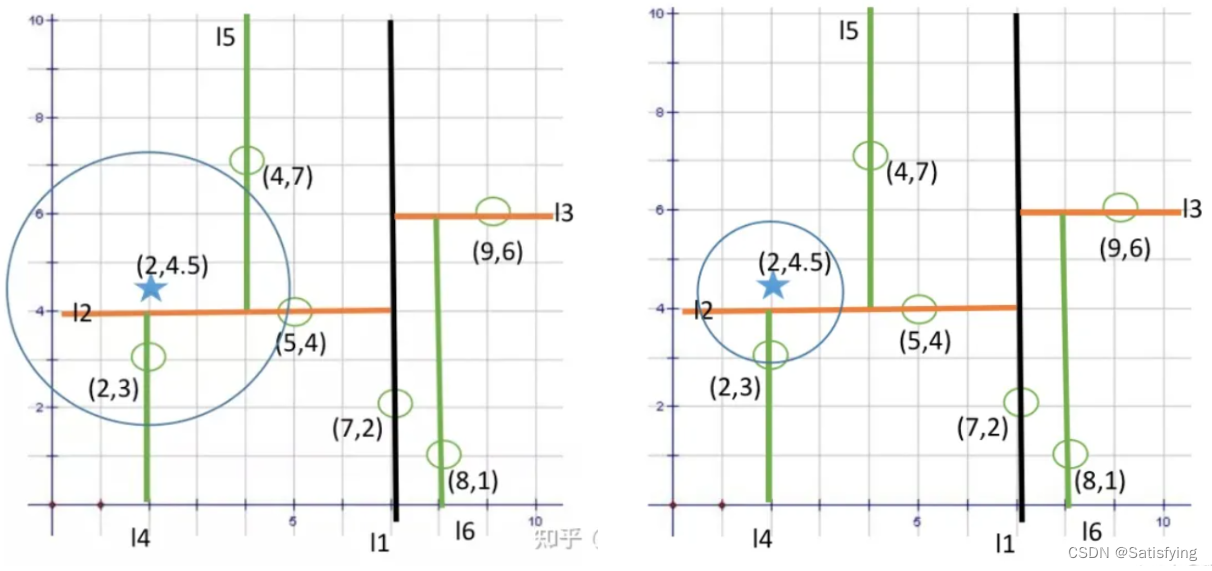
要求找到距离输入数据=2.1最近的节点,若使用线性搜索,那么需要进行7次比较,时间复杂度为
O
(
N
)
O(N)
O(N);
若使用二叉树搜索,只需要先和根节点4比较:2.1<4,此时记录最短距离d=1.9;进入左子树继续和2比较:2.1>2,更新最短距离d=0.1;进入右子树继续和3比较,此时两节点距离为0.9,0.9>0.1,因此最短距离就是0.1,且最近节点为2。使用二叉搜索树只需要3次就能找到最近节点,搜索的时间复杂度为
O
(
l
o
g
N
)
O(logN)
O(logN)。
## 三、KD-Tree
### 3.1 对KD-Tree的理解
**对于多维数据,可以使用二叉树在 K 维(在激光雷达中,一般使用三维点云,所以KD-Tree的维度K=3)空间上的扩展 KD-Tree**,它的时间复杂度也能近似达到
O
(
l
o
g
N
)
O(logN)
O(logN),实际上它的时间复杂度介于
O
(
l
o
g
N
)
O(logN)
O(logN)和
O
(
N
)
O(N)
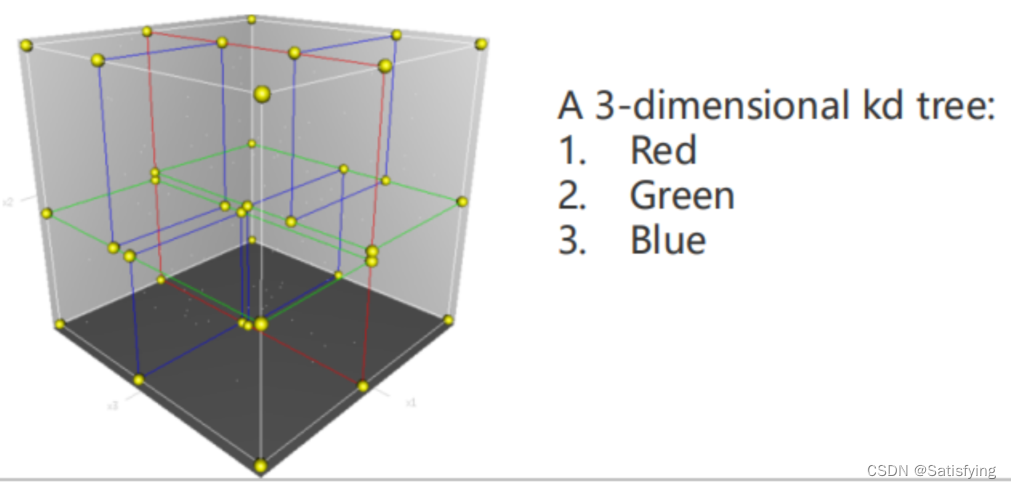
O(N)之间。\*\*KD-Tree本质上是一种特殊的数据结构——基于空间的平衡二叉树。\*\*KD-Tree是每个节点都有k维数据的平衡二叉树,每个节点代表一个超平面,该超平面垂直于当前划分维度的坐标轴,并在该维度上将空间划分为两部分。**KD-Tree两个关键问题:① 树的建立;②最近邻域搜索。**
**KD-Tree和二叉搜索树的不同点在于**,二叉搜索树每个节点只有一维特征,所以构建二叉搜索树时只需要根据这一维数据进行划分即可;对于多维数据,KD-Tree的划分策略是交替地使用每一维特征进行划分。KD-Tree会将三维空间分割成下图形式:
\*\*KD-Tree本质上就是一种数据结构,\*\*它的优点:① 搜索效率高;② 它是自平衡的,所以插入、删除数据也能保持高效;③ 易于实现。
### 3.2 生成KD-Tree
(1)初始化树深为
d
e
p
t
h
=
0
depth=0
depth=0和KD-Tree维度
K
K
K为数据维度;
(2)计算当前划分维度
s
p
l
i
t
=
d
e
p
t
h
%
K
split=depth\,\%\,K
split=depth%K,对当前维度数据进行排序并取其中位数;
(3)将该中位数作为分割点,并将其所在数据对作为当前根节点;
(4)将该维度数据小于该中位数的数据对传给当前根节点的左子树,将该维度数据大于该中位数的数据对传给当前根节点的右子树;
(5)递归执行步骤(2)~(4),直到所有数据都被建立到KD-Tree的节点上为止。
### 3.3 最近邻搜索
(1)从根节点出发进行查找,根据树深计算当前的分割维度split,若目标结点在分割维度上的数据小于当前节点,则进入左子树遍历,否则进入右子树遍历;
(2)重复步骤一,直到找到叶子节点,记录当前目标节点和当前节点的距离为最小距离,当前节点为最近节点,并开始回溯;
(3)回溯过程中若当前节点与目标节点距离更近,则更新最近节点及最小距离;并且判断是否需要遍历另一边子树:**若当前节点在分割维度上的数据与目标节点在分割维度上的数据间的距离小于当前最小距离,则进入另一边查找**,否则向上回溯;
(4)回溯到根节点,**同样比较根节点在当前分割维度上的数据与目标节点在分割维度上的数据间的距离小于当前最小距离**,则需要查找根节点的另一边子树,否则直接退出。
**整体思想:二分查找+回溯。**
\*\*细节点:\*\*回溯到某个节点,比较该节点和目标节点之间的距离时并不是计算欧氏距离(其实使用欧氏距离也可以),而是在当前分割维度上的数据之差,这是因为多维数据进行二分查找分割时,使用的是平行于某个坐标轴的超平面,\*\*每次判断是否查找另一边,是通过以目标节点为圆心,当前最小距离为半径做圆,判断当前分割面是否和该圆相交,\*\*如果不相交,那么说明该分割面另一边的点距离目标节点都更远,则不需要再查找;若相交,则说明分割面另一边可能存在距离目标节点更近的点,则需要查找另一边。
[Python手撸机器学习系列(十一):KNN之kd树实现]( )
[【精选】KD-Tree详解: 从原理到编程实现\_白鸟无言的博客-CSDN博客]( )
[最近邻搜索 KD树 生动图示理解笔记]( )
[【量化课堂】kd 树算法之详细篇 - JoinQuant量化课堂 - JoinQuant]( )
(批量查询参考:[机器学习——详解KD-Tree原理]( ))
### 3.4 Python代码
import numpy as np
import matplotlib.pyplot as plt
创建Node类型
class Node(object):
def init(self, value, left=None, right=None):
self.val = value
self.left = left
self.right = right
创建KDTree类型
class KDTree(object):
def init(self, K):
self.K = K
# 建树
def build_tree(self, data, depth):
l = len(data)
if l == 0:
return None
split = depth % self.K # 当前分割维度
sorted_data = sorted(data, key=lambda x: x[split]) # 按照某个维度数据进行排序
mid_idx = l // 2
left_data = sorted_data[:mid_idx]
right_data = sorted_data[mid_idx+1:] # mid_idx已经作为当前层根节点了,所以不能加mid_idx这个数据对
cur_node = Node(sorted_data[mid_idx]) # 将中位数作为当前根节点
cur_node.left = self.build_tree(left_data, depth + 1) # 递归构建当前根节点左子树
cur_node.right = self.build_tree(right_data, depth + 1) # 递归构建当前根节点右子树
return cur_node
# 计算欧氏距离
def cal_dis(self, point1, point2):
return np.linalg.norm(np.array(point1) - np.array(point2))
# 最近邻搜索(1个target)
def search_nn(self, tree, target):
self.near_dis = None
self.near_point = None
def dfs(node, depth):
if not node:
return
# 第一步要先找到叶子节点,之后再进行回溯
split = depth % self.K
if target[split] < node.val[split]:
dfs(node.left, depth + 1) # 该行包括下面的dfs行,第一个参数输入都是某个节点node.left或node.right,所以本质上该节点node并没有改变,每次改变的都是函数输入参数,所以当dfs递归结束并回退到该位置时,该节点没有变化,以此实现回溯上一个节点的过程!
else:
dfs(node.right, depth + 1)
# ======= 到这结束就已经找到了某个路径下最终叶子节点 =======
# 开始回溯,以当前叶子节点和目标节点的距离作为初始的最小距离
dis = self.cal_dis(node.val, target)
if not self.near_dis or dis < self.near_dis:
self.near_dis = dis
self.near_point = node.val
# 判断是否遍历该节点另一边子树
if abs(node.val[split] - target[split]) < self.near_dis:
if target[split] < node.val[split]: # 第一次从上往下遍历时目标节点值小于当前节点值时,就遍历左边;回溯时因为要遍历另一边,所以刚好相反!
dfs(node.right, depth + 1)
else:
dfs(node.left, depth + 1)
dfs(tree, 0)
return self.near_point
if name == “main”:
# dataset, target, K = [[2, 3], [5, 4], [9, 6], [4, 7], [8, 1], [7, 2]], [1, 5], 2
N_points, K = 64, 2
dataset = np.random.rand(N_points, K) # 生成随机的三维坐标数据
target = np.random.rand(1, K)[0] # 目标点坐标
tree = KDTree(K) # 构建kdtree类
my_tree = tree.build_tree(dataset, 0) # 使用数据构建kdtree
nearest_point = tree.search_nn(my_tree, target) # 求最近邻坐标点
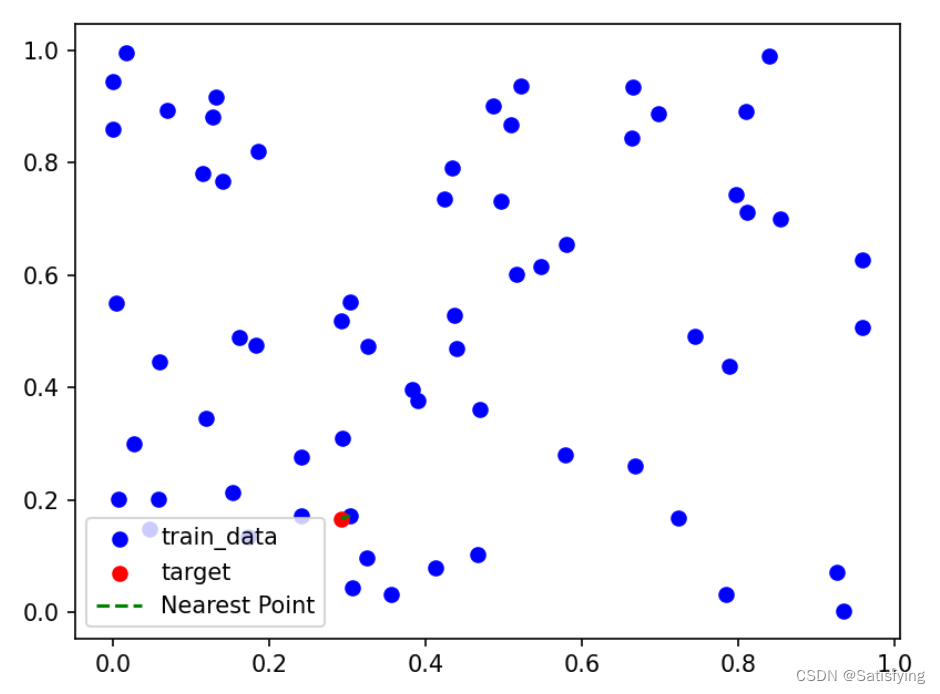
print('Nearest Point of {}: {}'.format(target, nearest_point))
plt.scatter([x[0] for x in dataset], [x[1] for x in dataset], c='blue', label='train_data')
plt.scatter(target[0], target[1], c='red', label='target')
plt.plot([nearest_point[0], target[0]], [nearest_point[1], target[1]], c='green', label='Nearest Point', linestyle='--')
plt.legend()
plt.show()
运行结果:
### 3.5 细节点理解
#### 3.5.1 分割维度的选择
**(1)选择方差最大的特征**
方差大说明该维度的数据相对分散,因此选择该特征进行分割可以获得更好的平衡。但可能会出现许多长条的分割,如右图。
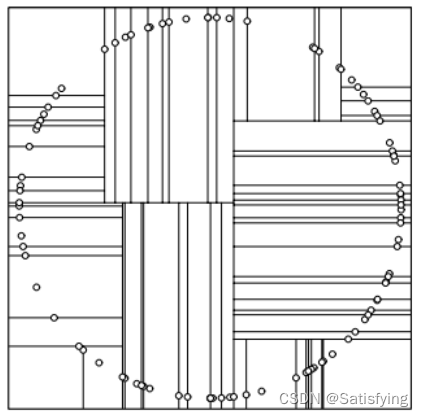
**(2)轮流选择**
**(1)Python所有方向的学习路线(新版)**
这是我花了几天的时间去把Python所有方向的技术点做的整理,形成各个领域的知识点汇总,它的用处就在于,你可以按照上面的知识点去找对应的学习资源,保证自己学得较为全面。
最近我才对这些路线做了一下新的更新,知识体系更全面了。

**(2)Python学习视频**
包含了Python入门、爬虫、数据分析和web开发的学习视频,总共100多个,虽然没有那么全面,但是对于入门来说是没问题的,学完这些之后,你可以按照我上面的学习路线去网上找其他的知识资源进行进阶。

**(3)100多个练手项目**
我们在看视频学习的时候,不能光动眼动脑不动手,比较科学的学习方法是在理解之后运用它们,这时候练手项目就很适合了,只是里面的项目比较多,水平也是参差不齐,大家可以挑自己能做的项目去练练。

**网上学习资料一大堆,但如果学到的知识不成体系,遇到问题时只是浅尝辄止,不再深入研究,那么很难做到真正的技术提升。**
**[需要这份系统化学习资料的朋友,可以戳这里获取](https://bbs.csdn.net/topics/618317507)**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








