目录
相反数:只有符号不同的两个数互为相反数,如:−a=a 0的绝对值还是0编辑
相反数和相反意义的数是不一样的,相反意义表示只要符号相反即可
绝对值:是指一个数在数轴上所表示的对应点到 原点的距离叫做这个数的绝对值,绝对值用“||”来表示。|a|
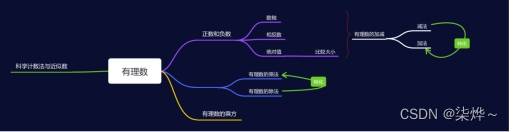
一,有理数的概念:整数和分数统称为有理数。
有理数方法1.按定义分类:

正整数,0,负整数统称为整数;
方法2,按符号分类

正分数,负分数统称为分数。<!--注:小数可以化成分数,分数也能化做小数-->
0是整数也是有理数即是自然数
小数化分数的时候,应该要化为10,100,1000.........为分母的数
如11.111 化为分数就是1000分之11111
二,数轴
数轴的定义:数轴(number axis) 规定了原点(origin),正方向和单位长度的一条直线叫数轴。所有的实数都可以用
在数学中,可以用一条直线上的点来表示数,这条线就叫做数轴
数轴它满足以下要求:
(1)在直线上任取一个点表示0这个点叫做原点(origin);
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示 1(向右1个单位长度),2(向右2个单位长度),3(向右3个单位长度),…;从原点向左,用类似方法 依次表示-1(向左1个单位长度),-2(向左2个单位长度),-3(向左3个单位长度)…
数轴的画法:画一条直线,规定一个原点,再选取一个适当的长度单位(实数)画点
注意点:实数和数轴是不分离的,模范夫妻一对一 的一个存在(实数)
数轴的三要素
一个数轴的三要素分别是 :原点,长度单位,正方向
利用数轴可以比较有理数的大小,数轴上从左往右的点表示的数就是按从小到大的顺序。
如何在数轴上画出表示一个数的点呢?
首先需要根据已知数的符合确定表示这个数的原点在哪边,
其次,从原点沿相应的放心确定它与原点相距的几个单位长度,从而确定这个点的位置!最后,在这个点上边写上对应的字母(或下边写上对应的数即可)
目前所有的 有理数都可以在数轴上用点来表示
三,相反数
数值相反的两个数,我们就说其中一个数是另外一个数的相反数。
定义:只有符合不同的两个数互为相反数
注意点:0的相反数是0。
例如:-2与+2互为相反数。用字母表示a与-a是相反数
这里a便是任意一个数,可以是正数、负数,也可以是0.
基本概念
相反数
- 相反数特性:若a.b互为相反数,则a+b=0,反之若a+b=0,则a、b互为相反数。
- 相反数是成对出现,不能单独出现。
- 要把"相反数"与"相反意义的量"区分开来。
- "相反数"不但是数的符号相反,而且符号后面的数字必须相同,如同:+2与-2。
- 而"具有相反意义的量"只要符号相反即可,如+2与-5。
- 求一个数的相反数只需这个数前面加上一个负号就可以了,若原数带有符号(不论正负),则应 先添括号。
- 数字a的相反数是-a,-a的相反数是a。这里的a不一定是正数(a表示任意一个数,可以是正 数、负数,也可以是0.),所以-a也不一定就是负数。
例如: a=0 时,则-a=0, 即a= -a
a<0时,则-a>0,即a<-a
a>0时,则-a<0,即a>-a
多重符合化简
求一个数的相反数只需这个数前面加上一个负号就可以了,若原数带有符号(不论正负),则应先添括号
例子:
-12读作“负12”,结合前面相反意义的学习,还可以赋予-12怎样的意义呢?我们可以把负12 理解为:12的相反数
类比
-15看作:15的相反数
-15 = -15
-(-15)可以看作:15的相反数的相反数
所以-(-15)= 15
-[ - ( -15 )]可以看作:15的相反数的相反数的相反数 感觉像在无限套娃
所以-[ - ( -15 )] = -15
那么:- [+ ( -15 )]可以看作什么呢?
分析:根据前面学习的知道,一个正数的符号可以省略
所以:- [+ ( -15 )] = - (-15)
-[+ ( -15 )]可以看作:15的相反数的相反数
-[+ ( -15 )] = 15
探索总结:
-15 = -15
-(-15)= 15
-[ - ( -15 )] = -15
-[+ ( -15 )] = 15
- 一个正数前面不管有多少个“+”号,都可以全部省略
- 一个正数前面偶数个”-“号,则化简后把”-“号一起去掉
- 一个正数前面奇数个”-“号,则化简后保留一个”-“
四,绝对值
绝对值:一般的是指一个数在数轴上所表示的对应点到 原点的距离叫做这个数的绝对值,绝对值用“||”来表示的 :|a|
例子:
36 的绝对值是 36 为什么?因为它距离原点的长度是36
-36的绝对值是36的相反数= 36,为什么?因为距离就是36!
0的绝对值就是它本身,距离也是0
以此来判断可以发现一个规律
任何有理数的绝对值都是大于0或等于0的数 简称:有理数的绝对值都是非负数
方法
结合有理数分为正数,负数和0,结合数轴,我们可以将求一个有理数的绝对值方法概况为:
一个正数的绝对值是它本身:若a≥0; 则|a|=a;
一个负数的绝对值是它的相反数:若a<0; 则|a|=-a(a的相反数);
0的绝对值是0 若a=0;则|a|=-a;
互为相反数的两个数的绝对值相等
重要结论:任何一个有理数a的绝对值总是非负数
符合表示:|a|≥ 0
有理数比较大小的方法
代数方法
正数大于0,负数小于0,正数大于负数
两个正数,绝对值大的数较大
两个负数,绝对值大的数反而小
异号两数比较大小,要考虑它们的正负,同号两数比较大小,要考虑它们的符号和绝对值
几何方法
利用数轴,数轴上左边的点表示的数比右边点表示的数小
五,有理数的加减乘除
有理数的加减法
有理数的加法
将一个或多个有理数的值相加的过程叫有理数的加法!
有理数加法的运算结果必然是有理数的。
如果有两个有理数做加法运算,试着思考一下会有几种情况?
正有理数 + 正有理数 正有理数 + 0 正有理数 + 负数
0 + 正有理数 0 + 0 0 + 负有理数
负有理数 + 正有理数 负有理数 + 0 负有理数 + 负有理数
可以发现有9种情况
小学学过的有
正有理数 + 正有理数 正有理数 + 0 0 + 0
中学要学的数有
负有理数 + 负有理数 负有理数 + 正有理数 负有理数 + 0
三种类型:
同号相加
(-8)+ (-4)= -12
负有理数 + 负有理数
异号相加
8+ (-5) = 3 (-8) + 5 = -3
负有理数 + 正有理数
一个数与0相加仍得这个数
0 + 有理数 = 有理数
注:可以利用数轴更加直观的去理解
要点规律
同号相加不变,异号相加变减.欲问符号怎么定,绝对值大号选
加法法则
加法:同号两数相加,取相同的符号,并把绝对值相加; 绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值; 一个数同零相加,仍得这个数。
有理数的减法
有理数的减法法则
减去一个数,等于加上这个数的相反数
符合表示为:a-b = a +(-b)
例子:(-2) - (-3) = (-2) + 3数轴
(-2) - (-3) = 1
如果大数减小数,那么大数减小数的差大于0; 如果 a>b,那么a - b > 0
如果小数减大数,那么大数减小数的差小于0; 如果 a<b,那么a - b < 0
如果相同两个数相减,差就等于0:
a等于b=0 (-3) - (-3) = 0
a和b互为相反数 = 两数绝对值相加 (-3) - 3 = -6 或 3 - (-3) = 6 不同的操作顺序结果也不同
减法的注意步骤!
首要要统一转化成加法运算
注意运算符合的变化
运算律简便计算
分数的运算要先通分再计算 最终结果要化成最简形式
加减混合运算
加减混合运算可以统一为加法运算
符合表示:a + b - c = a + b + (-c)
统一为加法运算剖析
(-7)-(+5) + (-4) - (-10)
平常的解法:(-7)-(+5) + (-4) - (-10)
解:(-7)+(-5) + (-4) + (10)
= (-16)+10
= -6
更加简便的:(-7)-(+5) + (-4) - (-10)
解:-7-5-4+10
= -16+10
= -6
注意这个更加简便的加法运算里面没有加减符号
-7-5-4+10表达的是负7负5负4正10 这个时候我们只要计算-7-5-4+10的和就可以了
1- 4 + 6 - 0.5
有理数加减混合运算基本小结
将加减混合运算统一为加法运算;
写成省略加号和括号的形式
利用加法运算律和加法法则进行计算
在使用加法运算律时,需遵循的原则:
互为相反数的数相结合;
能凑整数的数相结合;
同分母的数相结合;
有理数的乘除法
乘法
问题 1
3 x 4 = 12 依次 (-3)x 4 = -12
如果是这样的算式?该怎么解?
4 x (-3) = ?
(-8) x (-3) = ?
0 x (-8) = ?
问题2:观察一下,发现规律
2 x 4 = 8
2 x 3 = 6
2 x 2 = 4
2 x 1 = 2
2 x 0 = 0
2 x (-1) = -2
2 x (-2) = -4
以此内推..........
乘法法则
正数乘负数(负数乘正数),积为负数,积的绝对值等于各乘数绝对值的积
负数乘负数;积为正数,至于为什么可以上网搜索一下为什么
任何数与0相乘,积仍为0
两数相乘,同号得正,异号得负,并把绝对值相乘
倒数定义
回顾小学知识扩展
倒数定义:ab = 1;
正数的倒数是正数,比如3和3分之一;负数的倒数是负数,0没有倒数
数a(a != 0)的倒数是a分之一
多个有理数相乘的积的符号规律
1 x 2 x 3 x (-4) = -24
1 x 2 x (-3) x (-4) = 24
1 x (-2) x (-3) x (-4) = -24
(-1) x (-2) x (-3) x (-4) = 24
几个不是0的数相乘,积的符号由负因数的个数决定
当负因数的个数是偶数是,积为正
当负因数的个数是奇数是,积为负
简记为:“奇负偶正”
多个有理数乘法计算步骤
先观察是否有因数为0;
确定积的符号(奇负偶正);
确定积的绝对值。
除法
问题1:(-4)/ 2 = ?
小学的时候,我们所学的乘除,我们都知道被除数 / 除数 = 商 商 x 除数 = 被除数
根据除法是乘法的逆运算,要求一个数,使它这个数与2相乘 得 - 4。
因为:(-2)x 2 = - 4
所以:(-4)/ 2 = - 2
倒数方面:(-4)/ 2 = (-4) x 2分之一 = -2
于是我们可以:(-4) / 2 = (-4) x 2分之一
通过上述式子表明,一个数除以2可以转化为乘2的倒数来进行。
依照这个规律做一下题
如:(-15) / 5 = (-15) x 5分之1
所以:(-15) / 5 = (-3)
如:(-15) / (-3) = (-15) x 负3分之1
所以:(-15) / (-3) = 5
以此可知有理数除法法则:
第一种方法
除以一个不等于0的数,等于乘以这个数的倒数。
符号表示:a / b = a x b分之1 (b != 0)
第二种方法
(1). (-15) / 5 = (-3) (2). (-15) / (-3) = 5
由这个规律我们可以进一步得出:
同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0的数都得0
提示:乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后得结果,乘除混合同级运算时要按照从左到右进行计算(括号里的除外)
先乘除后加减(只在乘除加减混合运算里面运用)乘除混合就要从左到右
六,有理数乘方&科学记数与近似数
有理数的乘方
引例:
根据小学学过的知识
假如:一个正方体棱长为6cm的正方体
一面的面积为:6 x 6 = 12(cm²) 体积:6 x 6 x 6 = 18(cm³)
这个时候6记作:6² 6记作: 6³ 或6的三次方
如果:4个(-2)相乘 记作:(-2) 读作:”-2的4次方”
如果:n个5相乘 记作5ⁿ 读作:”5的n次方”
概念:求n个相同的因数的积的运算,叫做乘方,乘方的结果叫做幂。
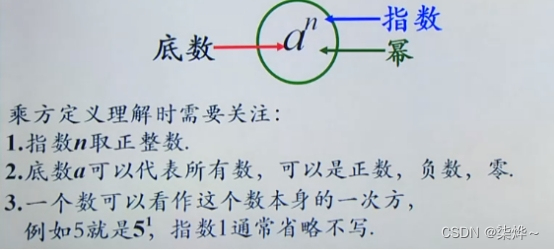
注:乘法的书写方式如果是负数一定要加括号,加括号表达的意思和不加是两个概念
不加括号的
-3⁴ (-3)⁴ 是不一样的
-3⁴ 次幂结果为:-81
(-3)⁴次幂结果为:81
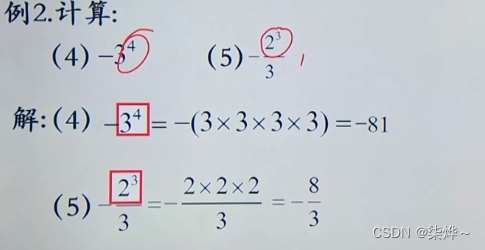
根据乘法的法则:我们可知:正数的次幂都是正数;负数的指数为奇数 次幂就是负数,反之偶数就为正数
0的任何正整数次幂都是正数

如果10^-5 ?
10^-5= 1 / 10^5 = 0.00001
有理数的混合运算
加减,乘除,乘方的混合运算顺序:
先乘方,再乘除,最后加减 三个级别
同级别运算,从左到右进行
如有括号,先做括号里,按小括号,中括号,大括号依次进行
科学计数法与近似数
科学计数法
把一个大于10的数表示成a x 10^n (其中a大于或等于1且小于10,n是正整数)
使用的是科学计数法
56000000000 = 5.6 x 10^10 表示更加简洁
a的确定:左边数第一个数字后面点小数点,去掉最后一个不是0的数字后面的所有0;
n的确定:原数的整数部分的位数减1
对于一个绝对值很大的负数,我们可以先用负数的相反数用科学计数法表示,再添加负号
10^-5 = 1 / 10^5 = 0.00001
近似数
3.1415926 取近似数

精确度的两种形式
精确到个位,十分位,百分位.......
精确到1,0.1,0.01
近似数的表示
根据要求,找准所在位的数字,再把这个数字后面的数字四舍五入
七,初略总结

数轴:一条定义了正方向,原点和长度单位的线,叫做数轴 |
相反数:只有符号不同的两个数互为相反数,如:−a=a 0的绝对值还是0 |
绝对值:是指一个数在数轴上所表示的对应点到 原点的距离叫做这个数的绝对值,绝对值用“||”来表示。|a| |
有理数加减:同号相加不变,异号相加变减.欲问符号怎么定,绝对值大号选 减去一个数,等于加上这个数的相反数 符合表示为:a-b = a +(-b) 有理数加减混合运算基本小结将加减混合运算统一为加法运算; 写成省略加号和括号的形式 利用加法运算律和加法法则进行计算 在使用加法运算律时,需遵循的原则: 互为相反数的数相结合; 能凑整数的数相结合; 同分母的数相结合
|
有理数的乘除法:乘法法则正数乘负数(负数乘正数),积为负数,积的绝对值等于各乘数绝对值的积 负数乘负数;积为正数,至于为什么可以上网搜索一下为什么 任何数与0相乘,积仍为0 两数相乘,同号得正,异号得负,并把绝对值相乘 除法法则:第一种方法 除以一个不等于0的数,等于乘以这个数的倒数。 符号表示:a / b = a x b分之1 (b != 0) 第二种方法 (1). (-15) / 5 = (-3) (2). (-15) / (-3) = 5 由这个规律我们可以进一步得出: 同号得正,异号得负,并把绝对值相除。 0除以如何一个不等于0的数都得0 提示:乘除混合运算往往先将除法化为乘法,然后确定积的符号,最后得结果,乘除混合同级运算时要按照从左到右进行计算(括号里的除外) 先乘除后加减(只在乘除加减混合运算里面运用)乘除混合就要从左到右
有理数的混合运算加减,乘除,乘方的混合运算顺序: 先乘方,再乘除,最后加减 三个级别 同级别运算,从左到右进行 如有括号,先做括号里,按小括号,中括号,大括号依次进行
|
有理数的乘方
|
科学计数法把一个大于10的数表示成a x 10^n (其中a大于或等于1且小于10,n是正整数) 使用的是科学计数法 |
























 979
979

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








