
加油!还有时间,期末考试只是一次检验,而你所累积的知识和努力却是无法被考试分数所衡量的(bushi)
但你再不学就真的来不及了!!!
一、概率的性质(填空题、选择题)
1️⃣加法公式:
- 对任意事件A,B,有P(AUB) = P(A) + P(B) - P(AB)
- 若AB两两不相容则有P(AUB) = P(A)+P(B)
⭕推广:
对任意事件4,B,C,有
P(AUBUC)
= P(A)+P(B)+P(C) - P(AB)-P(BC)-P(AC)+ P(ABC)
若A,B,C互不相容,则 P(AUBUC) = P(A)+P(B)+P(C)
2️⃣减法公式:
- 对任意事件AB 有 P(A-B)=P(A)-P(AB);
- 若B∈A(包含在A中),则有 P(B)≤P(A),且P(A-B)= P(A)-P(B) 大的事件发生的概率也大

记忆口诀:长杠变短杠,开口换方向
📜例题:
由加法公式得 P(AB)=P(A)+P(B)-P(AUB) = 0.5+0.7-0.8 = 0.4

例2:设4,B,C是三个事件,且P(A)=P(B)=P(C)=0.25,P(AB)=P(BC)=0,P(AC)=0.125,则A,B,C至少有一个发生的概率为________
解:P(AUBUC)
=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC)由于ABC包含在AB中(ABC看成AB和C相交,AB都0肯定是0),所以P(ABC) ≤ P(AB)=0,故 P(ABC)=0 代入公式,得到
P(AUBUC)=0.25+0.25+0.25-0-0-0.125+0=0.625.


二、条件概率(填空题)
条件概率: 事件A 发生的条件下,B 发生的概率为 P(B|A) = P(AB) ÷ P(A)
乘法公式: 若P(A)>0,则P(AB)=P(B|A)P(A)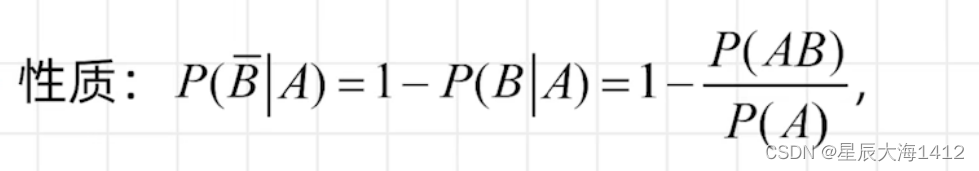
以上是对立事件发生的概率公式
如果加上A条件即加法公式
解:由加法公式 P(AUB) = P(A) + P(B) - P(AB),知 P(A)= 0.6+0.25-0.3 = 0.55
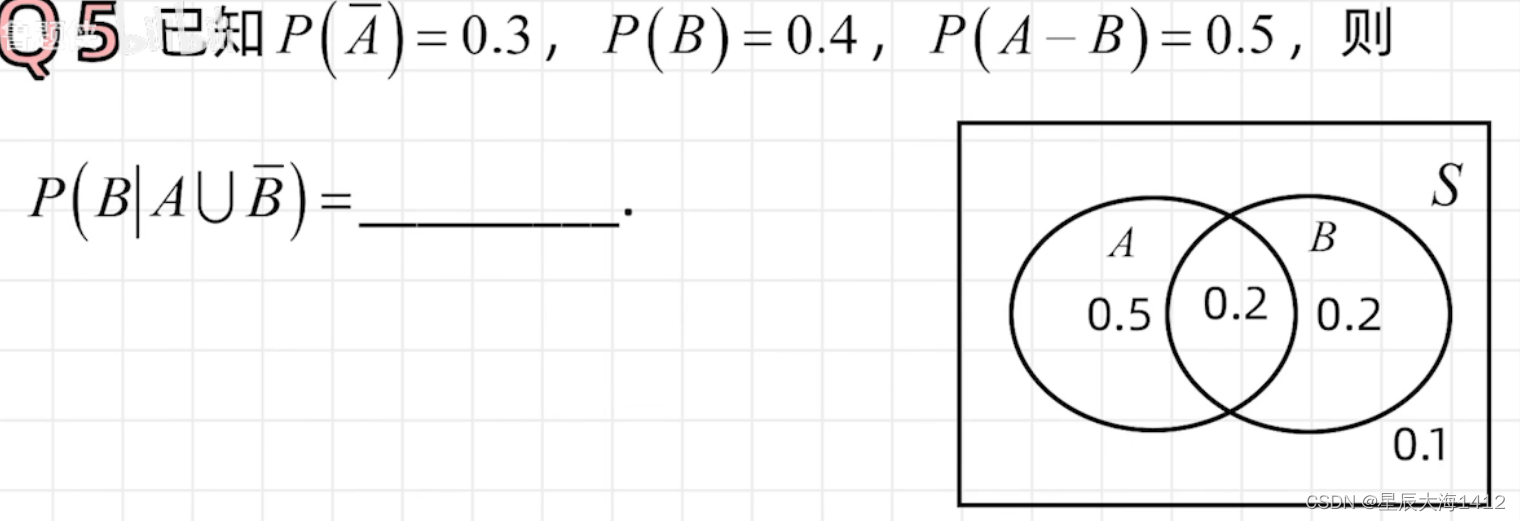
⭕ ∩写成乘,∪写成+
= 0.2 ÷ ( 0.7 + 0.6 -0.5 ) = 1/4
🌟随机事件和概率应试技巧总结
(1)无放回题目(一次摸多个)
- 例1. 盒子里有 3绿 4红 共7个小球,无放回的摸3个试求摸出 1绿 2红 的概率?
- 例2. 钱包里有3张100元,5张10元,3张5元的纸币,随机摸3张,试求摸出 1张100, 1张10 ,1张5元 的概率?

即答案为:


(2)有放回题目(进行多次,每次情况一致)
- 盒子里有 3绿 4红 共 7个小球,有放回的摸 3次 试求摸出 1绿 2红 的概率
- 某商场举行抽奖活动,每位用户可转下面奖盘3次,试求转3次奖盘,转出1次减免10元 2次谢谢参与的概率



✍🏻例题:盒子里有 3绿 4红 2粉 共9个小球,有放回的摸4次试求摸出 1绿 1红 2粉 的概率

(3)事件的概率①
📜例题:已知A、B相互独立,P(A) = 0.4,P(B)= 0.45

解题思路画图如下:
- 画一个面积为 1的方框
- 题干每有一个事件(字母),就在方框里画一个名称为该事的圆圈,暂时让各圆圈之间都有重合
- 根据 P(某事件) = 该事件对应区域的面积,调整每个圆圈的大小和位置
- 找出要求概率在图里对应的区域,算该区域的面积要求的概率 = 该区域面积

(4)事件概率题型②
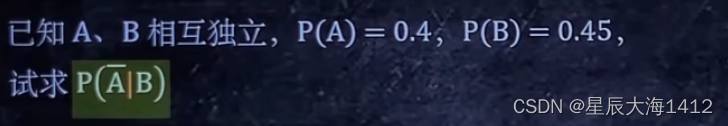
在已知 B 发生的情况下,A否 发生的概率

⭕A与B独立,那么 A否 与 B 也独立,要求的 P(A否|B)= P(A否) = 1 - 0.4 =0.6
(5)🌟全概率公式

✍🏻例题:某高速公路上客车中有 20% 是高速客车,80% 是普通客车,假设高速客车发生故障的概率是 0.002, 普通客车发生故障的概率是 0.01。求该高速公路上有客车发生故障的概率。

(6)🌟贝叶斯公式

✍🏻例题:某高速公路上客车中有 20% 是 高速客车,80% 是 普通客车,假设高速客车发生故障的概率是 0.002,普通客车发生故障的概率是 0.01。求该高速公路上⭕有客车发生故障时,发生故障的是高速客车的概率

✍🏻随机事件和概率题型总结
(1)古典概型(有放回、无放回)
①有放回
例题1️⃣:

✍🏻题型思路:
例题2️⃣:
假如你宿舍有哥儿10000个,中午抽签决定午饭吃什么,共有5张签2张写的鸡公煲,1张写的黄焖鸡,1张写的脆皮鸡,1张写的麻辣烫.你们10000个依次抽签,每人抽完后把签放回,则求哥儿10000个中有2000个去吃鸡公煲、4000个去吃黄焖鸡、2000个去吃脆皮鸡2000个去吃麻辣烫的概率。
②无放回

✍🏻 做题思路:

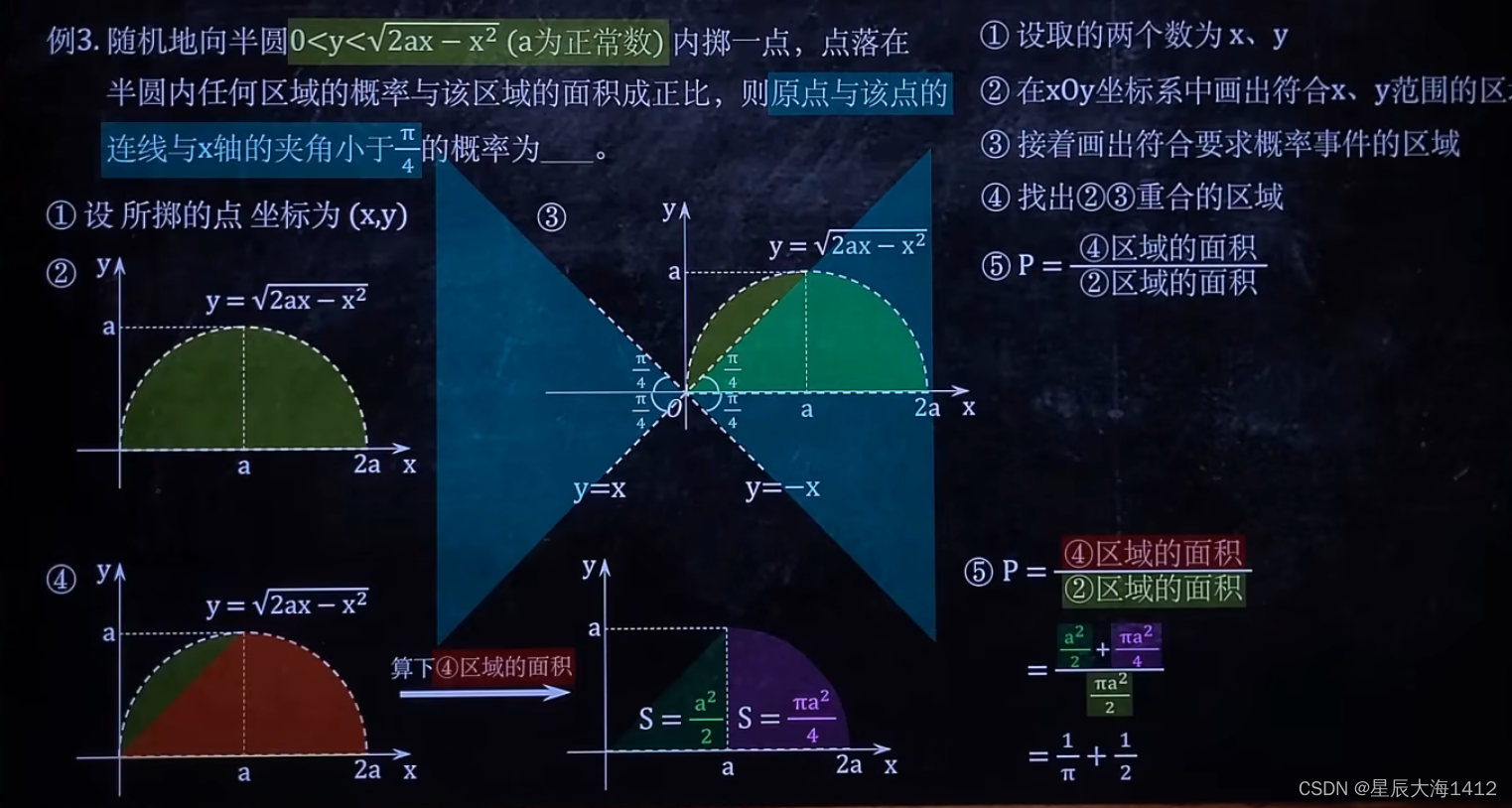
(2)几何概型

✍🏻做题思路:
(3)事件的概率

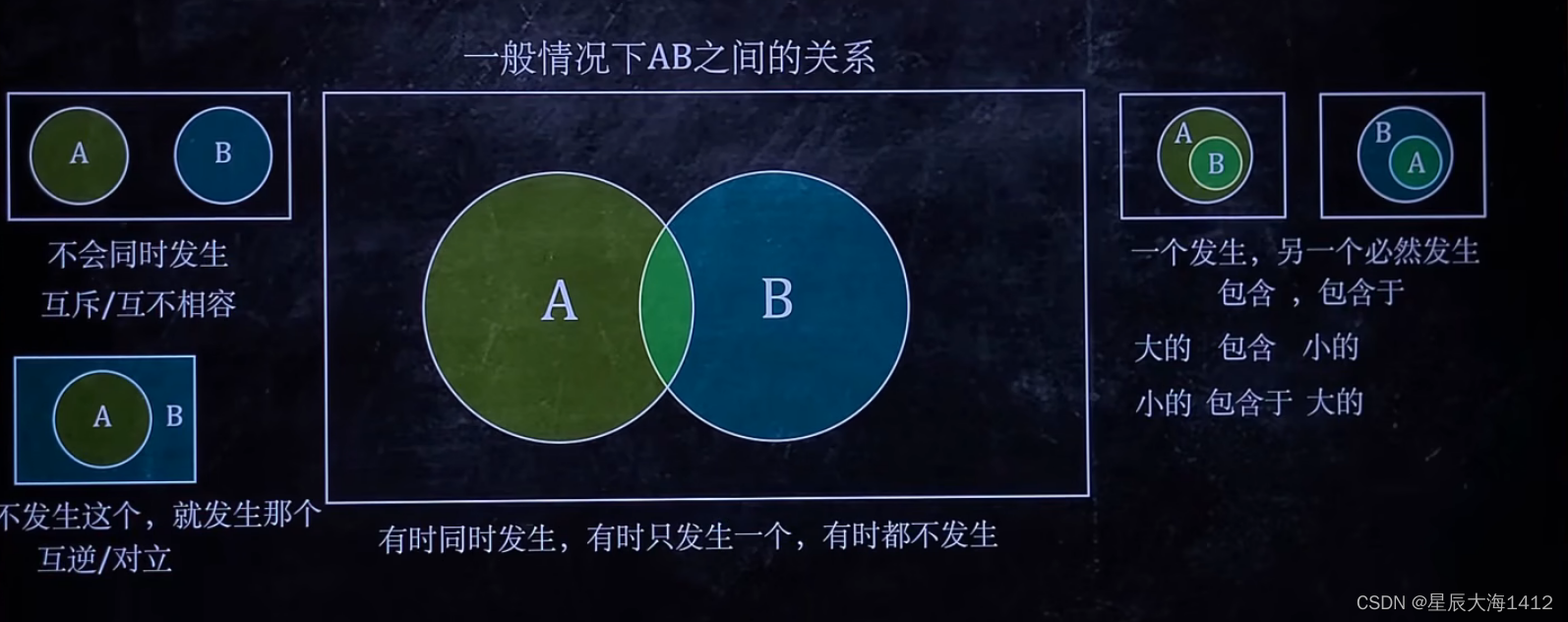


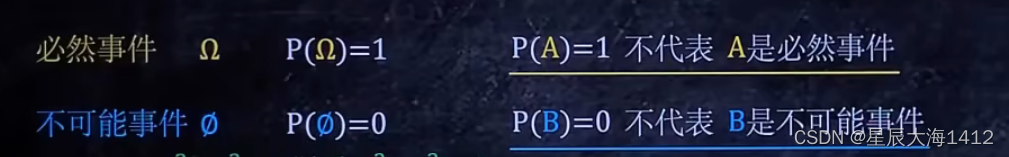

⭕ =1是可能发生的,因此<1不是必然发生的。这种情况不是必然发生的,那么就不是必然事件。
(4)事件的独立性

✍🏻解题思路:

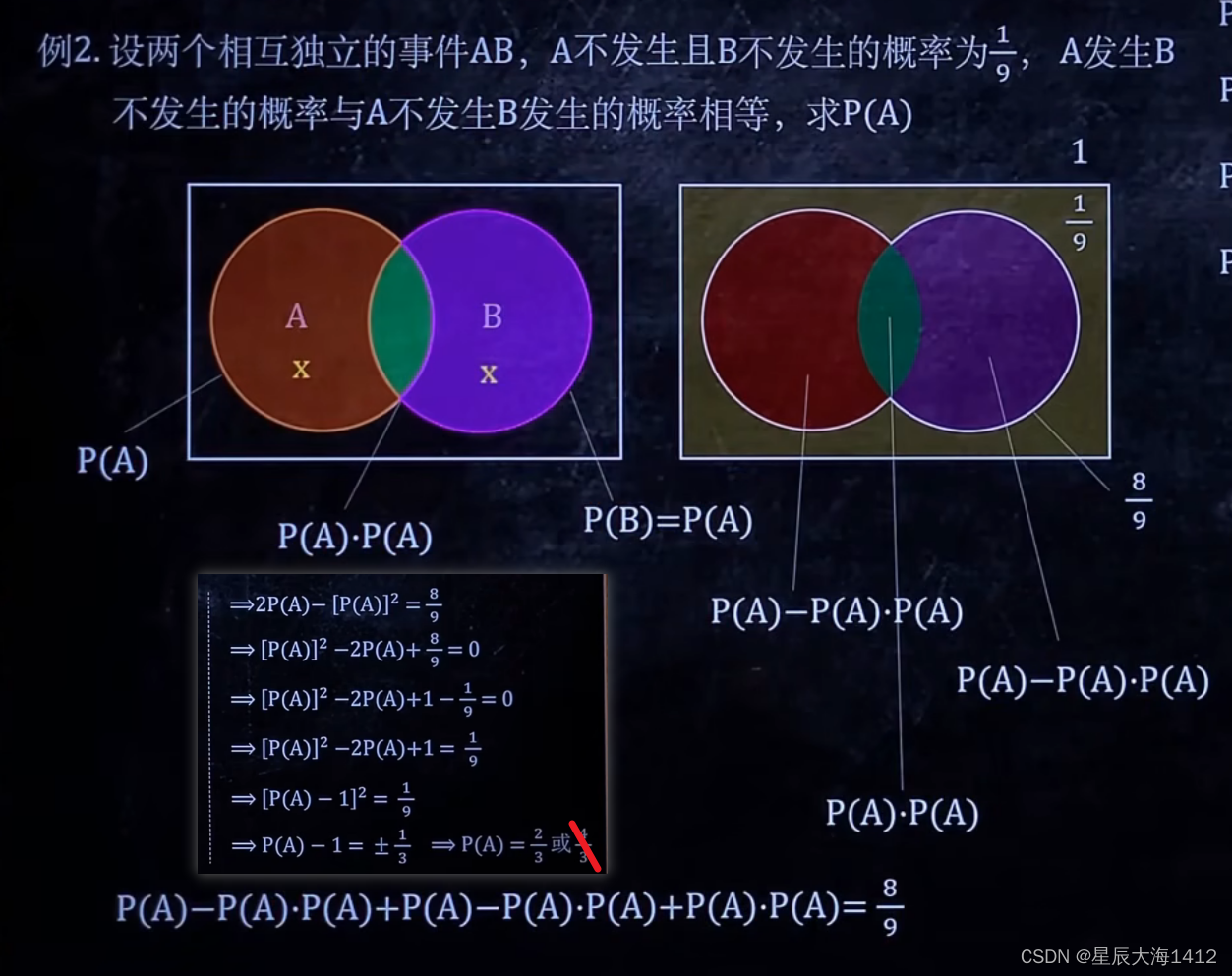
(5)条件概率

✍🏻解题思路:


(6)全概率公式

✍🏻解题思路:

(7)贝叶斯公式

✍🏻解题思路:


✍🏻推导图示关系:
三、🌟考点古典概型(填空题)
若随机试验的样本空间Ω只有有限个样本点,且每个基本事件发生的可能性相等,则事件A发生的概率为:
例题1️⃣:
在一副扑克牌 (52 张)中任取 4张,则4张花色金不相同的概率为_________。
解:每一张的概率都是相同的,且没有顺序关系。
四种花中各取一张(每一个花色各有十三张牌)

- 从M件次品中取m个,从 N - M 中选取 n - m 个
- 从N中选n 是整个事件发生的可能性
例题2️⃣:(抽样问题)
一个盒子中装有6(N)只杯子,其中有2只(m)不合格品,现做不放回抽样连续取2只(n),至少有1只是合格品的概率为_______。
例题3️⃣:
袋中有50个乒乓球,其中20个黄球,30个白球,今有三个人依次随机地从袋中各取一球,取后不放回,则第三个人取到黄球的概率是________。
解:由抽签原理知,第三个人取到黄球的概率与第一个人取到黄球的概率相等,为 2/5.
四、全概率与贝叶斯公式(大题)
①全概率公式

使用情况:A事件 可以被 B事件分割
②🌟贝叶斯公式
使用情况:已知A发生的概率去判断是属于哪一块的概率。(如果已知结果A发生了,判是那种情况时,要用贝叶斯公式)
贝叶斯公式(Bayes' theorem)是概率统计中的一项重要公式,用于更新对某个事件发生的先验概率(prior probability)基于观察到的证据来计算其后验概率(posterior probability)。
贝叶斯公式的一般形式如下:
P(A|B) = (P(B|A) * P(A)) / P(B)
其中,P(A|B)表示在已知事件B发生的前提下,事件A发生的概率,称为后验概率。P(B|A)表示在事件A发生的前提下,事件B发生的概率,称为似然度。P(A)表示事件A发生的先验概率,即不考虑观察到的证据时事件A发生的概率。P(B)表示事件B发生的先验概率,即不考虑观察到的证据时事件B发生的概率。
贝叶斯公式的核心思想是根据观测到的证据来修正先验概率,得到更准确的后验概率。它将概率问题转化为条件概率的计算,使得我们能够根据已有的信息和观测到的证据来进行推断和决策。
例题1️⃣:
设工厂甲 和工厂乙 的次品率分别是1%和2%. 现从甲厂 和乙厂 的产品分别占60%和40%的一批产品中随机抽取一件求
(1) 这件产品是次品的概率;
(2) 该次品是由甲厂生产的概率为
解:设A为“抽取的是次品”,B1表示“该产品来自甲厂,B2表示“该产品来自乙厂”
由题意,P(B1)=0.6,P(B2)=0.4,P(A|B1)=0.01,P(A|B2)=0.02
(1)出于事件A的发生可以分成两种情况
来自甲厂(B1),或来自乙厂(B2),A=AB1+AB2
由全概率公式,
P(A)= P(AB1)+ P(AB2)
= P(A|B1)P(B1)+ P(A|B2)P(B2) = 0.01x0.6+0.02x04 = 0.014(2)已知抽取的是次品,求它是甲厂生产的概率,用贝叶斯公式(已知结果,判断情况)
例题2️⃣:
两台车床加工同样的零件,第一台出现废品的概率为0.03第二台出现废品的概率为 002加工出来的零件放在一起,现已知第一台加工的零件比第二台加工的零件多一倍
(1)求任意取出一个零件是合格品的概率是多少?(利用对立事件求值)
(2)如果任取的零件是废品,求它是由第二台车床加工的概率
解:设A为 “取出的一件是废品”,B1为 “该零件由第一台车床加工”,B2为“该零件由第二台车床加工”
(2)由贝叶斯公式,所求概率为
五、事件的独立性(填空题、选择题)
例题1️⃣:
设事件A和B独立,P(B)=0.5
P(A-B)=0.3, 则P(B-A)=________。
由 0.3 = P(A-B) = P(A)-P(AB)
= P(A) - P(A)P(B) = P(A)-0.5P(A)
= 0.5P(A)
可知 P(4)=0.6. 因此 P(B-A) = P(B) - P(AB) = P(B) - P(A)P(B) = 0.5 - 0.6 x 0.5 = 0.2
例题2️⃣:
某人向同一目标重复射击,且每次射击相互独立,设每次命中目标的概率为P(0<p<1),则此人第三次射击时恰好是第二次命中的概率为________。
解:设A表示“第i次命中”,那么所求事件可分成2种情况:
第一次 第二次 第三次 中 未中 中 未中 中 中 第一种情况发生的概率为:
第二种情况发生的概率为:
⭕第五次射击 时恰好是 第三次命中 的概率是多少?
六、离散型随机变量分布律与分布函数互求(填空题、选择题)

分布律:①非负性,②全部概率和为1
例题:

解:由所有概率之和为1,得到p= 1 - 0.1 - 0.6 =0.3
- ≤ 全在左侧,而 <全在右侧,即右连续
- 给点可求得概率变化,因此可以发布函数、分布律互求

解:P(X=I) = P(X≤1) - P(X≤-1) = F(1) - F(-1) = 0.8 - 0.2 = 0.6.
实际上,由例13的分析,可知的分布律为
X
-1 1 3 P 0.2 0.8 - 0.2 = 0.6 1 - 0.8 = 0.2
七、二项分布和泊松分布(填空题、选择题) - 常见的离散型随机变量

- 当试验次数确定,每次试验的成功概率也确定,并且试验之间相互独立时,可以使用二项分布。
- 当事件发生的次数不确定,但在一定时间或空间内具有平均速率,并且事件之间相互独立时,可以使用泊松分布。
例题1️⃣:
从学校乘汽车到火车站的途中有5个十字路口,假设在各个十字路口遇到红灯的事件是相互独立的,并且概率都是0.4,那么途中遇到2次红灯的概率是_________。
例题2️⃣:
设在3次相互独立试验中,事件A出现的概率相等,若已知A至少出现1次的概率19/27,是则A在一次试验中出现的概率为_________。
解方程,得到 p = 1 / 3

🌟连续型需要积分题型应试技巧总结

(1) 求分段函数在确定区间的定积分

✍🏻解题思路:
- 画出待求积分的上下限区域
- 根据 f 不同的取值范围,将区域分成几段
- 令待求积分 = 第一段区域积分 + 第二段区域积分 + ···



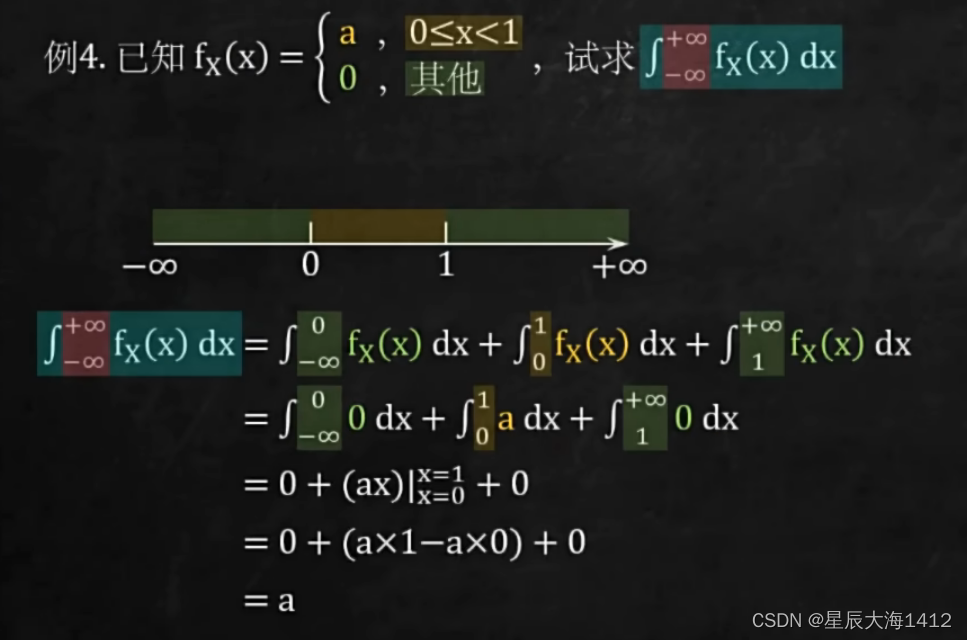



(2)求分段函数在-∞到未知数的定积分
✍🏻解题思路:
①画出 f式子 不同式子的范围
②设积分上限 ∈ 第一个范围,求积分
设 积分上限 ∈ 第二个范围,求积分
设 积分上限 ∈ 第三个范围,求积分
③将各种情况结果汇总在一个大括号里


(3) 求简单的二重积分

✍🏻解题思路:

(4)求 f(x,y) 的二重积分
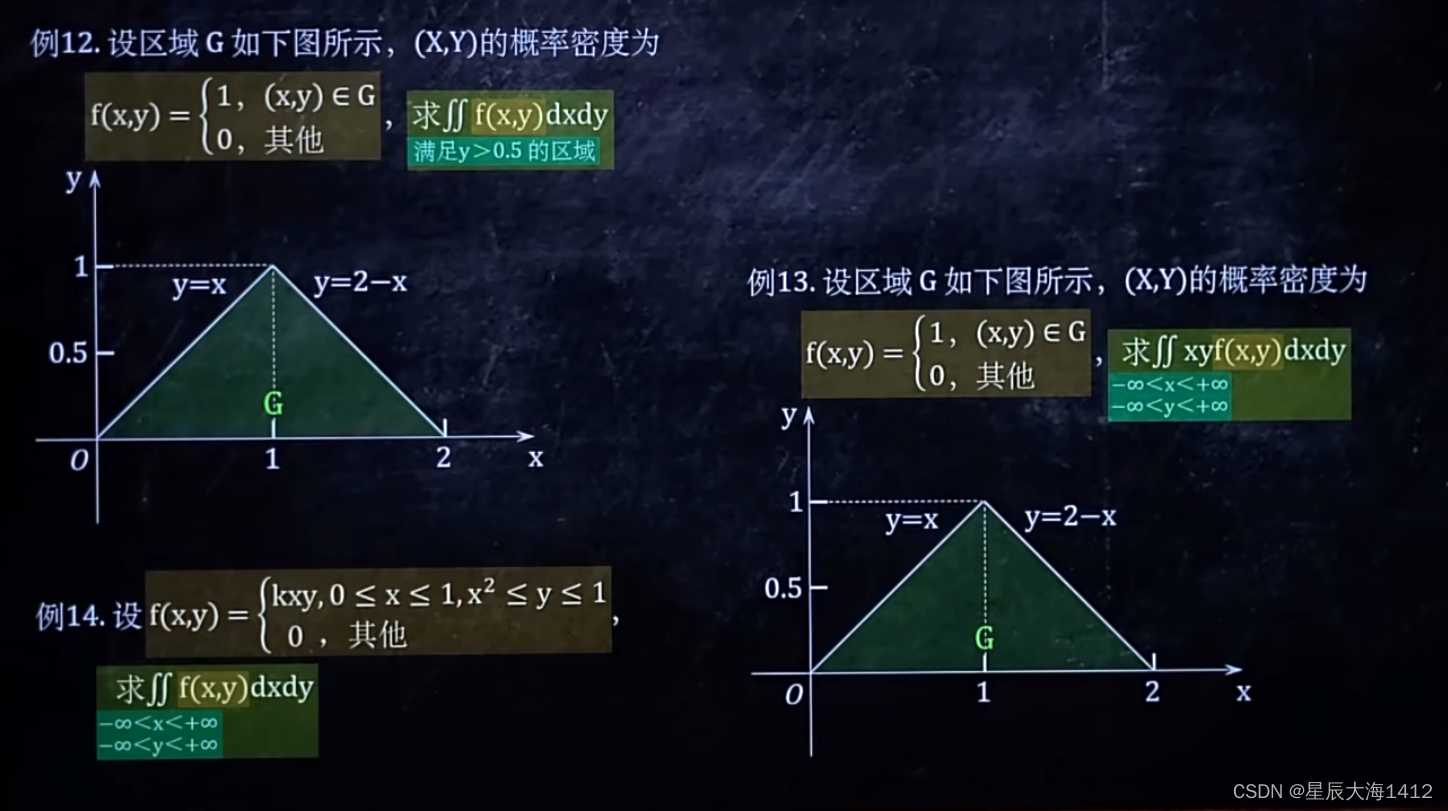
✍🏻解题思路:
🌟一维连续型随机变量应试解题技巧
(1)已知 fx(x) 求概率

✍🏻解题技巧:
(2)求 fx(x) 中的未知数
(3)已知 fx(X)求F

✍🏻解题思路:
(4)求 F 中的未知数
✍🏻解题思路:

(5)已知 F 求 f
✍🏻解题思路:
(6)已知 f 求 f

✍🏻解题思路:


(7)已知 f 求期望、方差
✍🏻解题思路:

🌟离散型随机变量题型总结
(1)一维离散型 求分布律
离散型 VS 连续型

一维离散型 题型如下:
✍🏻解题思路:
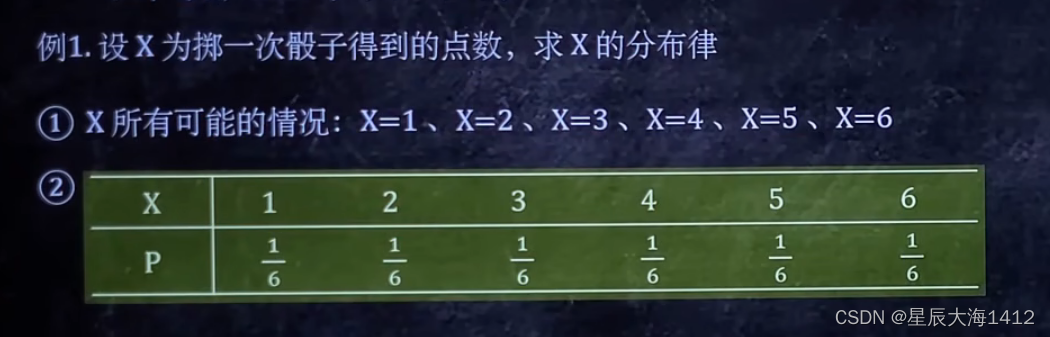



⭕不用分布律里是因为题目没说事件A、B相互独立

(2)二维离散型 求分布律
✍🏻解题思路:

(3)二维离散型 求 边缘分布律

(4)一维离散型求分布函数
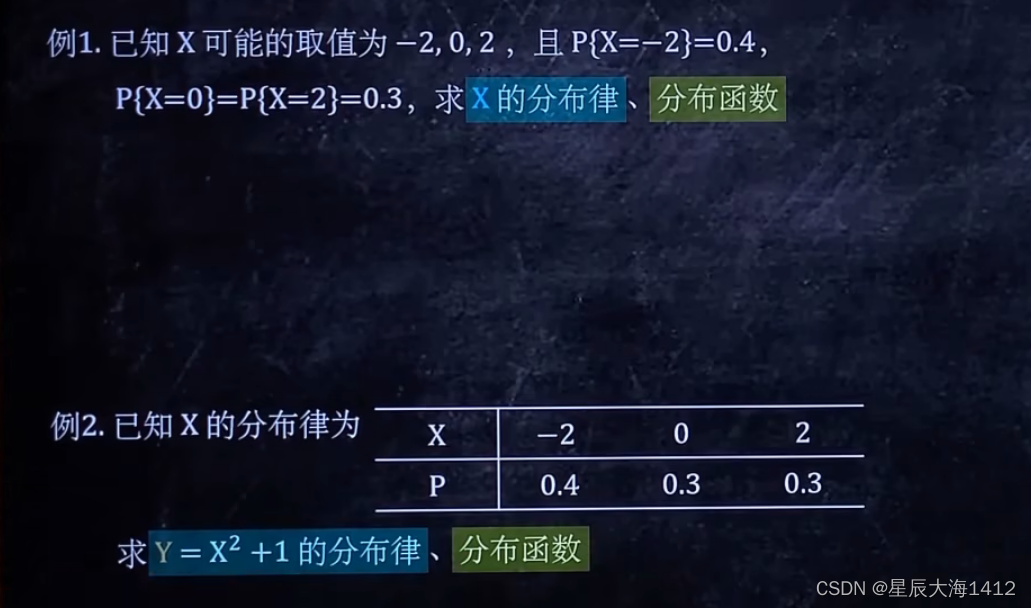
✍🏻做题思路:


(5)二维离散型 求分布函数
✍🏻做题思路:

⭕注意:

(6)🌟一维离散型求期望、方差

✍🏻做题思路:


(7)二维离散型 求期望、方差

✍🏻连续型随机变量 题型总结
(1)一维连续型求概率

✍🏻解题思路:

🌟积分常用公式:

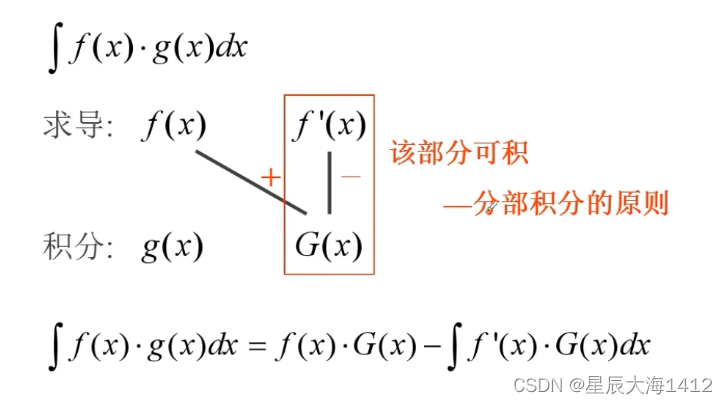
分部积分法口诀:上导下积,斜线相乘,竖线相积,正负交替
例题:









(2)二维连续型求概率

✍🏻解题思路:










八、🌟关于连续型随机变量概率的计算(填空题、大题)

- 离散型随机变量分布函数为求和,连续型是随机变量函数是取积分
- 取某一个固定点的概率为0,即不用考虑端点的情况,是否加等号并不影响概率的值。

-∞ 可看为0代入
当x ≥ 1 时,F(x)=1.(即包含所有的概率)
- 从 a 到 b 的概率即是函数从 a 到 b 的积分
- 密度函数又是非0的,因此积分下限从0开始积
- 分布函数也可求概率
九、均匀分布(填空题) - 常见连续型随机变量①

均匀分布是一种概率分布,它的定义式可以如下表示:
对于一个随机变量X,如果其取值范围在[a, b]之间,且在该范围内的每个数值都有相等的可能性,则称X服从均匀分布。
记作:X ~ U(a, b)
其中,a和b是分布的参数,表示均匀分布的上下界。这意味着在[a, b]区间内的任何一个值的概率密度函数(PDF)为常数,表示该值出现的概率与其他值相等。
均匀分布的概率密度函数(PDF)为:
f(x) = 1 / (b - a),a <= x <= b
其中,f(x)表示随机变量X取值为x的概率密度。
均匀分布的累积分布函数(CDF)为:
F(x) = (x - a) / (b - a),a <= x <= b
其中,F(x)表示随机变量X小于等于x的概率。
⭕注意:均匀分布是在给定范围内所有值的概率相等,而不考虑取值范围外的情况。此外,均匀分布还可以有离散和连续两种形式,上述定义式适用于连续均匀分布。

⭕有实根即求取值在两个数之间的概率之和
0.2 是根据均匀分布的定义式提前算出来的 f(x) = 1/(6-1) = 0.2
十、正态分布(填空题、选择题) - 常见连续型随机变量②




- 正态分布函数标准化如上
- X - μ / σ 得到的随机变量即标准正态随机变量
- 把随机给的正态分布转化为标准正态分布,方便后面的转换和查表

十一、离散型随机变量 函数的分布(填空题)


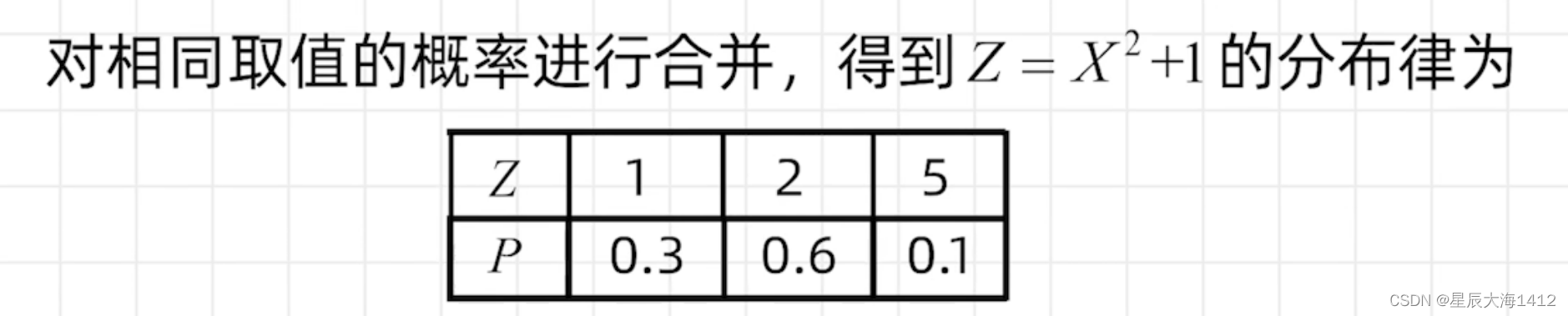
⭕需要对Z取值相同的概率进行合并
十二、连续型随机变量函数的分布(填空题、与连续型随机变量分布函数、概率等 结合的大题)


⭕ (3/2)x^2 -> (积分)(1/2)x^3,然后代入“根号y”(根号y = y的(1/2)次方)

⭕(4)x>0时,3x=y-1,3x>0,y-1>0,y>1
🌟离散型随机变量应试技巧总结
(1)求分布律里的未知数
✍🏻例题①:
已知的分布律为
| X | -2 | 0 | 2 |
| P | 0.4 | 0.3 | k |
试求 k。
解:0.4+ 0.3 + k = 1 => k= 0.3
例题②: 
解:2/3 + 1/12 + a + 1/12 = 1 => 1/6
X的取值要么是0要么是1,概率分别是2/3,a。
(2)根据X的分布律写Y的分布律


(3)根据(X,Y)的分布律写 Z 的分布律


(4)根据(X,Y) 的分布律写边缘分布律

(5)X 与 Y 相互独立时的联合分布律
设随机变量X与Y相互独立,下表列出了二维随机变量(X,Y)的联合分布律及关于X和关于Y的边缘分布律中的部分数值,试将其余数值填入表中的空白处

- 1/6 = y1x1 + 1/8
- P{ X = x2 } = 1/8 + x2y2 + x2y3
- x1y1 + x2y1 = 1/8
- P{ X = x1 } + P{ X = x2 } = P{X,Y} = 1
- P{ X=x1 } * x1y2 = P{ Y = y2 }
(6)根据分布律求期望、方差
已知X的分布律为
| X | -2 | 0 | 2 |
| P | 0.4 | 0.3 | 0.3 |
Y的分布律为
| Y | 1 | 5 |
| P | 0.3 | 0.7 |

求方差公式:DX = E(X^2) - (EX)^2
🌟六种常用随机变量的期望与方差,期望与方差的性质

十三、二维离散型随机变量的分布(填空题、大题)



十四、二维连续型随机变量的分布(大题)

- 离散型随机变量是把满足条件的所有概率相加
- 连续型则是求积分
- 二维连续型则是求二重积分


把 y 积分掉剩下就是关于 x 的函数

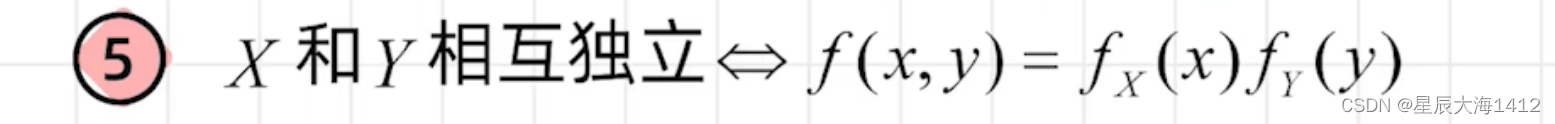

⭕(-y)dy+(6-x)dy=-1/2y^2+(6-x)y,上下限为2,4

十五、离散型随机变量函数的分布(填空题、大题)


十六、连续型随机变量函数的分布(填空题、选择题、大题)






十七、数学期望(填空题、大题)


十八、方差和标准差(填空题、大题)

二维离散型

🌟常用分布的期望和方差(填空题)


⭕X2是正态分布


















































































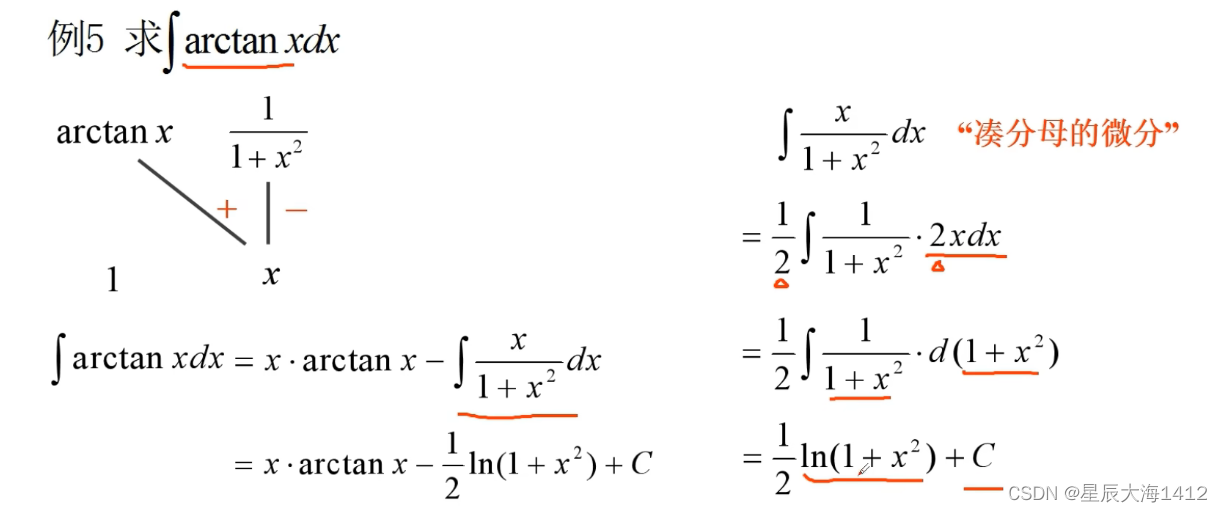



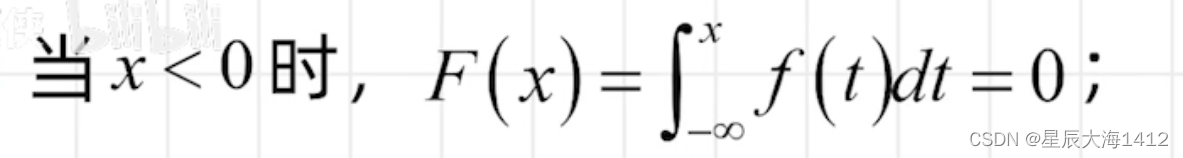

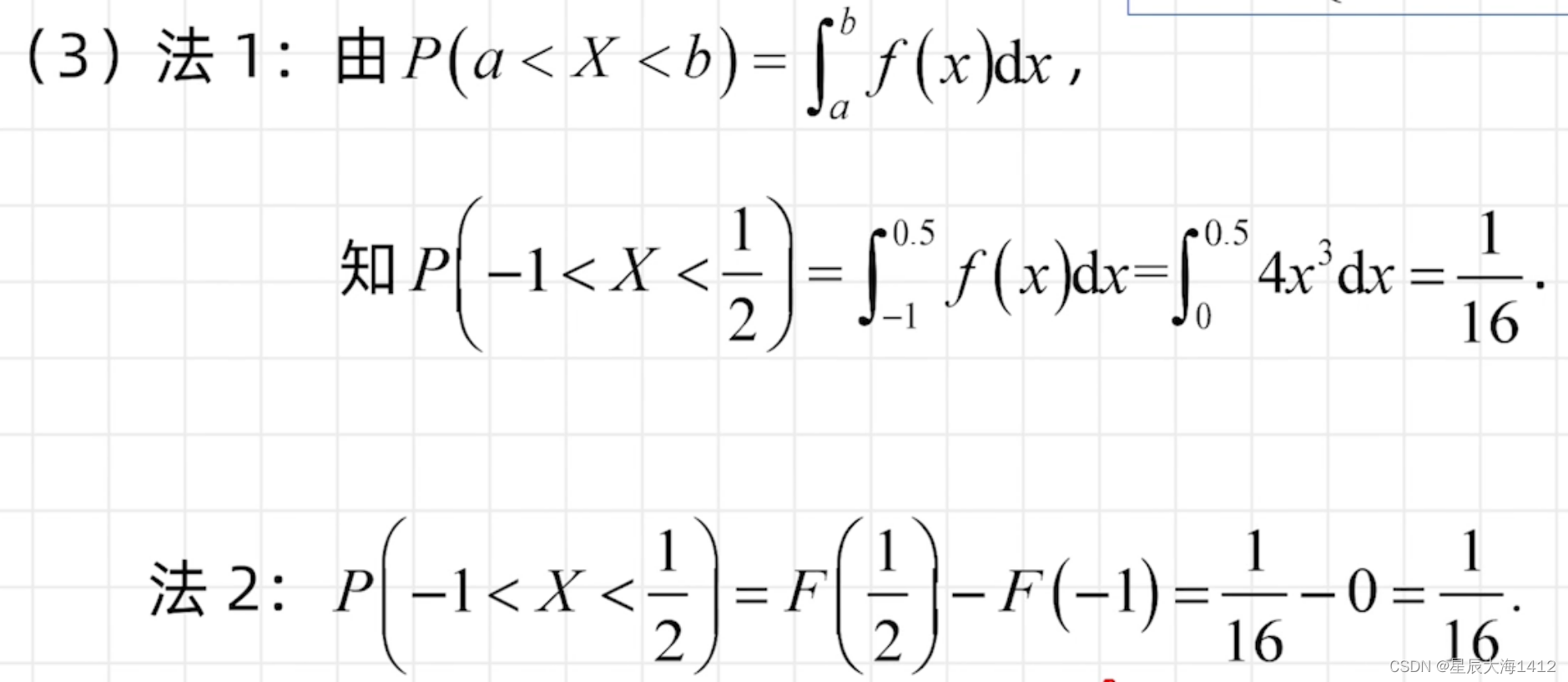






























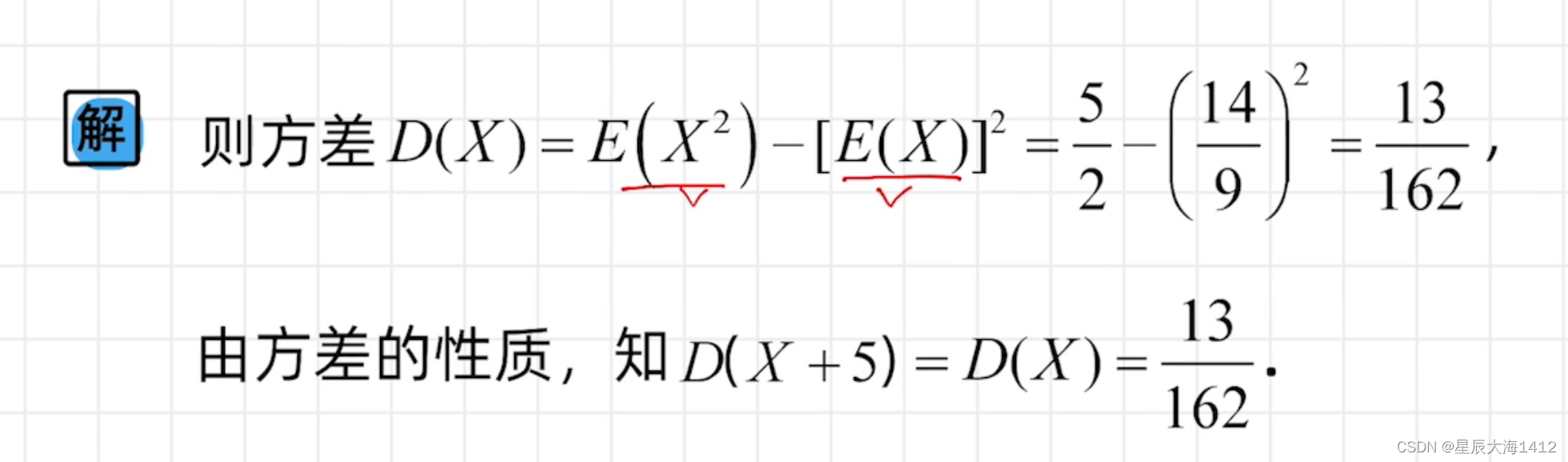




















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








