递归算法之全排列生成（Permutations）详细解读

最新推荐文章于 2025-04-07 21:53:44 发布

Katie。

最新推荐文章于 2025-04-07 21:53:44 发布

阅读量1.9k

点赞数 11

分类专栏：算法分析文章标签：算法

本文链接：https://blog.csdn.net/m0_61840987/article/details/143138744

版权

算法分析专栏收录该内容

87 篇文章

订阅专栏

全排列（Permutations）是指从给定的 nnn 个元素中，按照某种顺序进行排列，生成所有可能的顺序组合。全排列是排列组合中的一个重要问题，在算法、数学、以及计算机科学中有着广泛的应用。

全排列问题的目标是生成某个集合的所有排列。例如，给定集合 {1, 2, 3}，其全排列为：

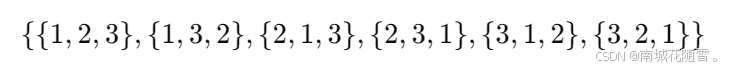
1. 全排列的定义

给定一个包含 n 个不同元素的集合，要求输出所有元素的不同排列，具体指的是把这 n 个元素按照不同的顺序排列。例如，集合 {a,b,c}的所有排列为：

全排列的数量为 n!（阶乘），即 n 个元素有 n 种排列方式。对于 n 个元素，排列数公式为：

2. 全排列的生成算法

全排列问题可以通过递归、回溯、以及字典序法等多种方法来生成。

2.1 递归生成全排列

递归生成全排列的核心思想是：将问题分解为较小的子问题。设定一个指针 index 指向当前处理的元素，将该位置的元素与之后的每个元素交换，然后递归处理剩下的元素。

递归生成全排列的步骤：

交换当前位置元素与后续位置元素。
递归处理当前位置的后续子序列。
回溯，即将元素交换回原来的位置，继续处理其他的排列情况。

递归实现 Java 代码：

import java.util.ArrayList;
import java.util.List;

public class Permutations {
    
    // 主方法，生成并返回所有的全排列
    public static List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> result = new ArrayList<>();
        backtrack(nums, result, 0);
        return result;
    }
    
    // 回溯法生成全排列
    private static void backtrack(int[] nums, List<List<Integer>> result, int index) {
        // 当 index 指向数组末尾时，表示已生成一种排列，将其加入结果集中
        if (index == nums.length) {
            List<Integer> currentPermutation = new ArrayList<>();
            for (int num : nums) {
                currentPermutation.add(num);
            }
            result.add(currentPermutation);
            return;
        }
        
        // 递归地交换元素生成不同的排列
        for (int i = index; i < nums.length; i++) {
            swap(nums, index, i);      // 交换当前元素与后续元素
            backtrack(nums, result, index + 1); // 递归处理下一个元素
            swap(nums, index, i);      // 回溯：将数组恢复原状
        }
    }
    
    // 交换数组中的两个元素
    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        List<List<Integer>> permutations = permute(nums);
        for (List<Integer> permutation : permutations) {
            System.out.println(permutation);
        }
    }
}

代码详解：

permute 方法是生成全排列的入口，初始化结果集，并调用回溯法 backtrack。
backtrack 是核心递归函数，index 表示当前处理到的元素位置。若 index 到达末尾，说明生成了一个完整的排列，加入结果集。
在每一层递归中，遍历后续元素，将其与当前元素交换以生成新的排列。递归调用后再交换回来，称为回溯，继续生成其他排列。
swap 方法用于交换数组中的两个元素。

递归算法的时间复杂度：

生成 n个元素的全排列，其时间复杂度为 O(n!)，因为总共有 n! 种排列。
递归深度为 n，每次递归涉及数组元素的交换操作。

2.2 非递归的字典序法

字典序法生成全排列的思路是按照字典序的顺序生成排列，从最小的排列开始，不断生成下一个排列直到所有排列都生成完毕。它适合用于那些需要按顺序生成排列的场景。

字典序法生成全排列的步骤：

找到当前排列的第一个不满足升序的元素对 nums[i]<nums[i+1]
找到该元素后面最小的大于它的元素 nums[j]，并交换它们。
将 i 后面的部分反转，以获得下一个字典序排列。

字典序法 Java 实现：

import java.util.Arrays;

public class NextPermutation {
    
    // 生成下一个字典序排列
    public static boolean nextPermutation(int[] nums) {
        int n = nums.length;
        int i = n - 2;

        // 从后向前找到第一个升序的数对 (i, i+1)
        while (i >= 0 && nums[i] >= nums[i + 1]) {
            i--;
        }

        // 如果不存在下一个排列，则返回 false
        if (i < 0) {
            return false;
        }

        // 从后向前找到比 nums[i] 大的最小元素 nums[j]
        int j = n - 1;
        while (nums[j] <= nums[i]) {
            j--;
        }

        // 交换 nums[i] 和 nums[j]
        swap(nums, i, j);

        // 反转 i+1 到末尾的元素，恢复最小字典序
        reverse(nums, i + 1, n - 1);

        return true;
    }

    // 交换数组中的两个元素
    private static void swap(int[] nums, int i, int j) {
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
    }

    // 反转数组的某个子区间
    private static void reverse(int[] nums, int start, int end) {
        while (start < end) {
            swap(nums, start, end);
            start++;
            end--;
        }
    }

    public static void main(String[] args) {
        int[] nums = {1, 2, 3};
        do {
            System.out.println(Arrays.toString(nums));
        } while (nextPermutation(nums));
    }
}