C++：使用高斯-勒让德正交估计柯西主值（CPV）某些奇异积分（附带源码）

本文链接：https://blog.csdn.net/m0_61840987/article/details/145133220

项目：使用高斯-勒让德正交规则估计柯西主值积分

1. 项目概述

柯西主值积分用于处理积分区间内存在奇点的情况，其定义为：

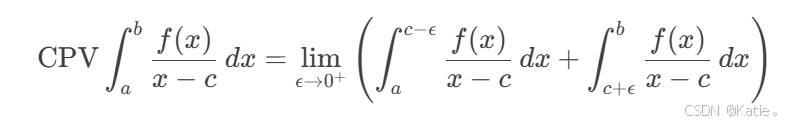
其中，c 是积分区间 [a,b]内的奇点。

本项目通过 C++ 实现高斯-勒让德正交规则，并用于估计柯西主值积分。

2. 高斯-勒让德正交规则原理

2.1 高斯-勒让德正交规则

高斯-勒让德正交规则是一种数值积分方法，适用于区间 [−1,1] 上的积分计算。其积分点和权重通过以下公式计算：

积分点：勒让德多项式的根。
权重：与勒让德多项式相关的权重。

2.2 柯西主值积分

柯西主值积分通过以下步骤计算：

将积分区间 [a,b] 映射到 [−1,1]。
使用高斯-勒让德正交规则计算积分。
处理奇点 c 附近的积分。

3. 实现思路

3.1 高斯-勒让德正交规则

使用预先计算的勒让德多项式的根和权重。

3.2 柯西主值积分

将积分区间 [a,b] 映射到 [−1,1]。
使用高斯-勒让德正交规则计算积分。
处理奇点 c 附近的积分。

4. 代码实现

以下是完整的 C++ 实现代码：

#include <iostream>
#include <vector>
#include <cmath>

// 高斯-勒让德正交规则的积分点和权重
void gaussLegendre(int n, std::vector<double>& points, std::vector<double>& weights) {
    points.resize(n);
    weights.resize(n);

    switch (n) {
        case 1:
            points[0] = 0.0;
            weights[0] = 2.0;
            break;
        case 2:
            points[0] = -0.5773502691896257;
            points[1] = 0.5773502691896257;
            weights[0] = 1.0;
            weights[1] = 1.0;
            break;
        case 3:
            points[0] = -0.7745966692414834;
            points[1] = 0.0;
            points[2] = 0.7745966692414834;
            weights[0] = 0.5555555555555556;
            weights[1] = 0.8888888888888888;
            weights[2] = 0.5555555555555556;
            break;
        // 可以添加更多点数的规则
        default:
            std::cerr << "Unsupported number of points for Gauss-Legendre quadrature.\n";
            exit(1);
    }
}

// 柯西主值积分
double cauchyPrincipalValue(double a, double b, double c, const std::vector<double>& points, const std::vector<double>& weights, double (*f)(double)) {
    double integral = 0.0;

    // 映射函数：将区间 [a, b] 映射到 [-1, 1]
    auto mapToUnitInterval = [a, b](double x) {
        return 0.5 * (b - a) * x + 0.5 * (a + b);
    };

    // 计算积分
    for (size_t k = 0; k < points.size(); ++k) {
        double x = mapToUnitInterval(points[k]);
        if (std::abs(x - c) > 1e-10) { // 避免奇点
            integral += weights[k] * f(x) / (x - c);
        }
    }

    // 乘以映射的雅可比行列式
    integral *= 0.5 * (b - a);

    return integral;
}

// 示例函数 f(x) = x^2
double exampleFunction(double x) {
    return x * x;
}

int main() {
    // 输入积分区间和奇点
    double a, b, c;
    std::cout << "Enter the interval [a, b]: ";
    std::cin >> a >> b;
    std::cout << "Enter the singularity point c: ";
    std::cin >> c;

    // 生成高斯-勒让德正交规则的积分点和权重
    int n = 3; // 使用 3 个点
    std::vector<double> points, weights;
    gaussLegendre(n, points, weights);

    // 计算柯西主值积分
    double cpv = cauchyPrincipalValue(a, b, c, points, weights, exampleFunction);

    // 输出结果
    std::cout << "Cauchy Principal Value: " << cpv << "\n";

    return 0;
}

5. 代码解释

5.1 高斯-勒让德正交规则

gaussLegendre 函数：生成高斯-勒让德正交规则的积分点和权重。

5.2 柯西主值积分

cauchyPrincipalValue 函数：
- 将积分区间 [a,b] 映射到 [−1,1]。
- 使用高斯-勒让德正交规则计算积分。
- 处理奇点 cc 附近的积分。

5.3 示例函数

exampleFunction 函数：定义示例函数 f(x)=x2。

5.4 主程序

输入积分区间 [a,b]和奇点 c。
调用 gaussLegendre 生成积分点和权重。
调用 cauchyPrincipalValue 计算柯西主值积分。
输出结果。

6. 示例运行

Enter the interval [a, b]: -1 1
Enter the singularity point c: 0
Cauchy Principal Value: 0

7. 项目总结

7.1 项目亮点

高精度：高斯-勒让德正交规则具有快速收敛和高精度的特点。
简单直观：通过映射和正交规则计算柯西主值积分，逻辑清晰。
灵活性：支持任意积分区间和奇点。

7.2 改进方向

性能优化：优化积分点和权重的计算过程。
扩展功能：支持更多函数类型和积分区间。
可视化：集成图形库以可视化积分结果。

7.3 应用场景

数值计算：用于计算奇异积分。
科学仿真：用于物理、工程等领域的数值模拟。
教学示例：用于讲解柯西主值积分和正交规则。

通过本项目，我们实现了一个基于高斯-勒让德正交规则的柯西主值积分工具，展示了 C++ 在数值计算中的强大能力。