矩阵乘法基本概念及模板题目

矩阵乘法（如下图所示）：

设第一个矩阵是A*B，第二个矩阵是B*C，那么乘出来得到的就是A*C

两个矩阵相乘的模板：

void mul(int a[][],b[][],c[][])
{
    for(int i=1;i<=A;i++)
    for(int j=1;j<=C;j++)
    for(int k=1;k<=B;k++)
    c[i][j]=a[i][k]*b[k][j];
}

常用场景：矩阵快速幂

矩阵乘法具有结合律如A*B*C==A*(B*C),当遇到A*(X*X*X*...*X)时就可以算法后面的X^n用快速幂来解决先。

传送门：1303. 斐波那契前 n 项和 - AcWing题库

思路：回顾斐波那契数列可以知道f[n]=f[n-1]+f[n-2]

现在定义一个向量F[n]= [ f[n] , f[n+1] ] , F[n+1]=[ f[n+1] ,f[n+2] ]，其余看下图：

由上式可以逐渐推出F[n]的表达式，F[n]=F[1]*A^(n-1),其中F[1,1]=[1,1],后半部分的A就是上图中的01行列式，快用快速幂求它的次方

对于题目中的S[n],可以将F[n]变成一个带有S[n]的向量，F[n]= [ f[n] , f[n+1]，S[n] ]

F[n+1]=[ f[n+1] ,f[n+2] , S[n+1] ],至于推法形如下图：

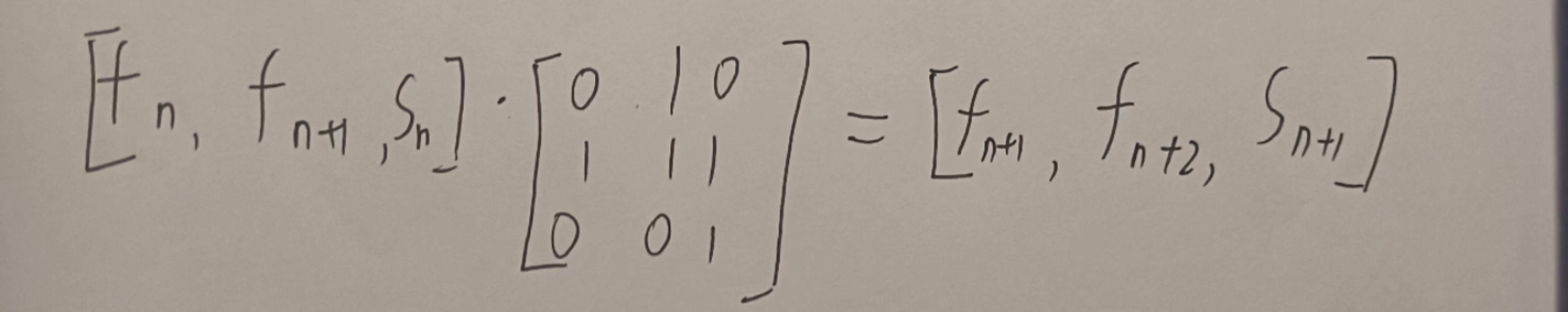
代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=3;
typedef long long ll;
 int n,m;
int a[N][N]={
    {0,1,0},
    {1,1,1},
    {0,0,1}
};
void mul(int a[],int b[][N])
{
    int tmp[N]={0};
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        tmp[i]=(tmp[i]+(ll)a[j]*b[j][i])%m;
        
    memcpy(a,tmp,sizeof tmp);//不能放传进来的C在sizeof后面，C是个形参
}
void mul(int a[][N],int b[][N])
{
    int tmp[N][N]={0};

    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        for(int k=0;k<N;k++)
        tmp[i][j]=(tmp[i][j]+(ll)a[i][k]*b[k][j])%m;
    memcpy(a,tmp,sizeof tmp);
}

int main()
{
    scanf("%d%d",&n,&m);
    int f1[N]={1,1,1};
    n--;
    while(n)
    {
        if(n&1) mul(f1,a); //相当于res*a操作
        mul(a,a);  //相当于快速幂里面的a*a操作
        n>>=1;
    }
    cout<<f1[2]<<endl;
    return 0;
}

又或者只用一个函数：

代码：

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=3;
typedef long long ll;
 int n,m;
int a[N][N]={
    {0,1,0},
    {1,1,1},
    {0,0,1}
};

void mul(int a[][N],int b[][N])
{
    int tmp[N][N]={0};

    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        for(int k=0;k<N;k++)
        tmp[i][j]=(tmp[i][j]+(ll)a[i][k]*b[k][j])%m;
    memcpy(a,tmp,sizeof tmp);
}

int main()
{
    scanf("%d%d",&n,&m);
    int f1[N][N]={1,1,1};
    n--;
    while(n)
    {
        if(n&1) mul(f1,a); //相当于res*a操作
        mul(a,a);  //相当于快速幂里面的a*a操作
        n>>=1;
    }
    cout<<f1[0][2]<<endl;
    return 0;
}

——————————————分割线——————————————

斐波那契数列的扩展：

传送门： 佳佳的 Fibonacci

思路：新的要求的 T(n)和原本的S(n)不同，不能像S(n)一样用S(n-1)+F(n)表示，但可以像下图里面一样用式子2减去式子1之后得到一个新的不含额外变量的式子，

新的式子用p(n)表示为n*S(n)-T(n),p(n+1)也可以表示为p(n)+s(n)

最后设一个四元向量F(n)表示[ f[n] , f[n+1] , S[n] , p[n]],可以得出F[n]=f[n-1]*A,F[n]=F[1]*(A^(n-1)) ,接着用矩阵快速幂来做。

代码：
 

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
const int N=4;
typedef long long ll;
 int n,m;
int a[N][N]={
    {0,1,0,0},
    {1,1,1,0},
    {0,0,1,1},
    {0,0,0,1}
};

void mul(int a[][N],int b[][N])
{
    int tmp[N][N]={0};

    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        for(int k=0;k<N;k++)
        tmp[i][j]=(tmp[i][j]+(ll)a[i][k]*b[k][j])%m;
    memcpy(a,tmp,sizeof tmp);
}

int main()
{
    scanf("%d%d",&n,&m);
    int f1[N][N]={1,1,1,0};
    int k=n;
    n--;
    while(n)
    {
        if(n&1) mul(f1,a); //相当于res*a操作
        mul(a,a);  //相当于快速幂里面的a*a操作
        n>>=1;
    }
    cout<<(((ll)k*f1[0][2]-f1[0][3])%m+m)%m<<endl;
    return 0;
}