动态规划哪里难了？这么多年都是这个难度(上)

开篇

本文可能和你以前所见的直接讲动态转移方程的动态规划文章不同，笔者在学习动态规划期间，也看过很多类似的教程，感觉对于萌新的我一脸蒙蔽，感觉就是像高中数学老师拿着答案给我们讲解一样。

本文按照算法导论的思路由递归演化到动态规划，带你感受其中的优化

还有人会说up，up，我会用递归解出来了，还要啥动态规划啊，这不是吃咸鱼蘸酱油 —多此一举吗？

咋要是都能轻松AC，代码优雅，高效，还要啥动态规划啊，

递归代码人偷懒了，关键是费机器，慢，特别容易超时

但是也不是说递归的思想就很简单了，我一直觉得递归几乎可以贯穿所以的算法，而用的好可以用最简单的代码完成任务，因为递归的黑盒特性，这点在二叉树章节想必大家有所体会。

而且对于优化比较好的code面试官也会对你印象深刻些，和其他人有区分度

我觉得在最前面我需要先说一些你从教材和算法导论上的基础概念和思想，

如果你觉得初学无法理解这么多名词那么多总结的思想，可以先跳过，我会在文章的最后再去把贪心，分治，回溯，动态规划这几种算法在放在一起对比一下使用场景

使用动态规划通常用来求解全局的最优解问题，为了求解全局最优解所有很自然的想到计算出所有的解然后返回最优解，而动态规划的核心思想就是 用于子问题重叠的情况，即不同的子问题具有公共的子子问题。动态规划算法对每个子问题只求解一次，将其解保存到一个表格中，避免重复计算，最后将这些子问题组合可以得出一个最优解

一句话总结就是每次计算完只有记录在表中，然后依靠表中的数据进行计算；

大家常见的动态规划步骤

• 1.创建dp 理解其含义
• 2.递推公式 -状态转移方程
• 3.初始化dp数组
• 4.遍历顺序，计算结果

这里的每一步都非常重要，当你做的题够多就明白你出错可能是某一步有问题
这里我们先用一个最简单的爬楼梯问题举例说明各种方法并且逐渐进阶
题目:leetcode 70.爬楼梯

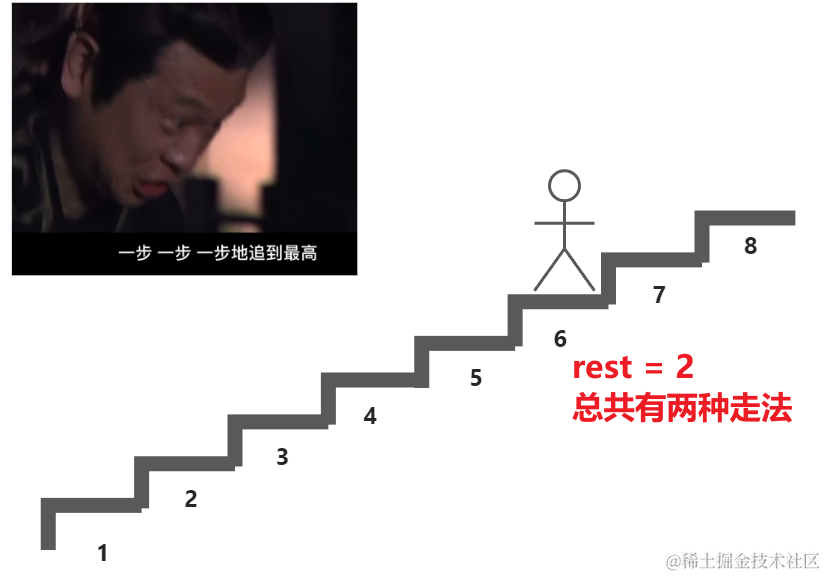
假设你正在爬楼梯，需要n阶才能到达楼顶 ，每次你可以爬1个或者2个台阶，。

返回你有多少种不同的方法爬到楼顶。

本文中的代码你也可以上leetcode去运行

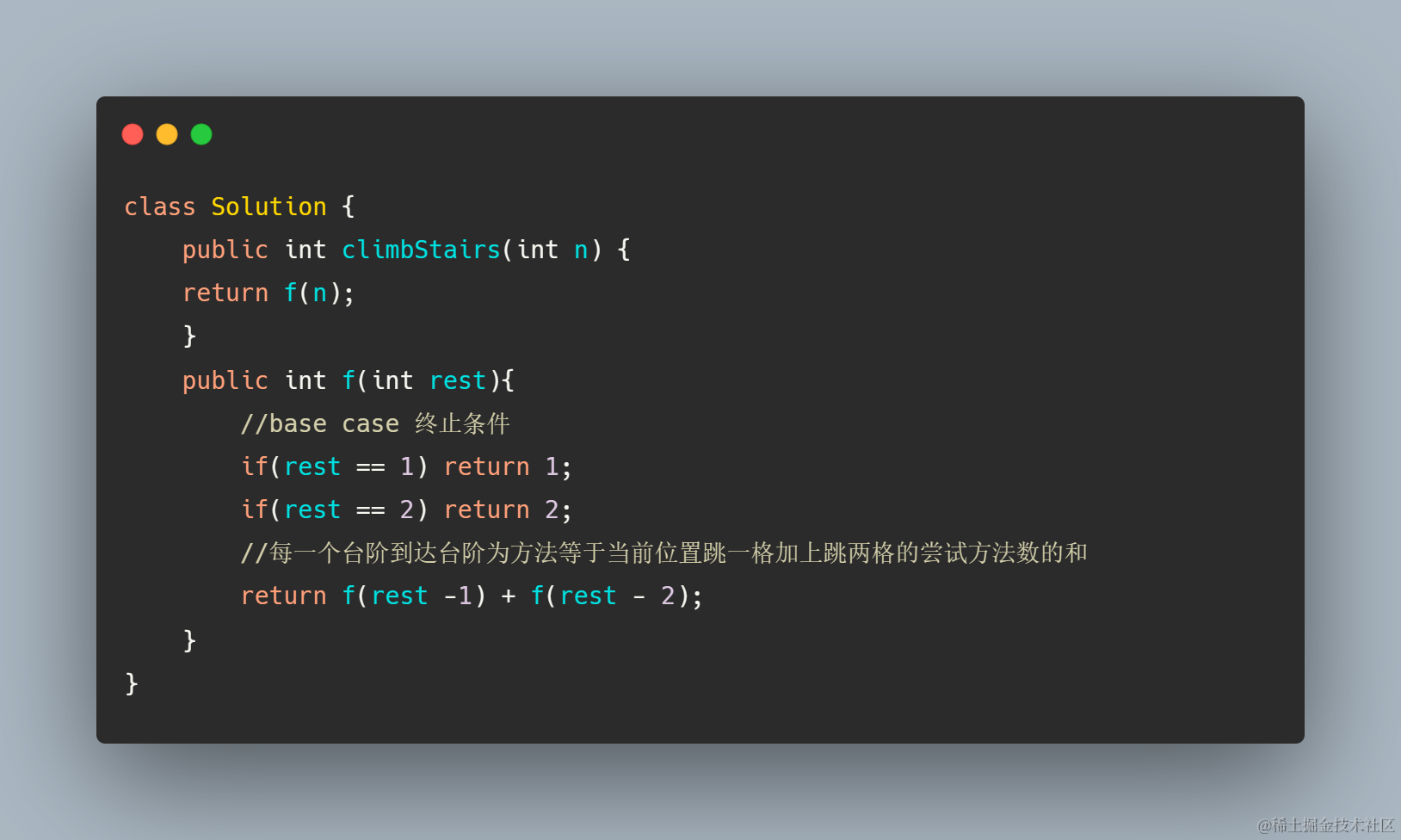
最初始版本 朴素暴力递归尝试-回溯

递归思想其实和回溯思想很像，就是无脑穷举尝试所有值，很好理解,想求解全局最优解必然是穷举所有可能性，然后对比选出最优解

每一个台阶到楼顶的路径数 等于当前位置跳一格加上跳两格的尝试方法数的和

递归三部曲为

• 1.递归的返回值 和 参数列表 //返回值应该是尝试的路径数 ,参数列表是剩余多少爬完
• 2.确定递归的终止条件 //倘若递归计算到，rest等于0步代表爬到楼顶了，返回一种成功的尝试
• 3.递归单层逻辑 每一层都是递归的计算当前层的尝试路径数 等于rest - 1和 rest - 2 的尝试路径数和

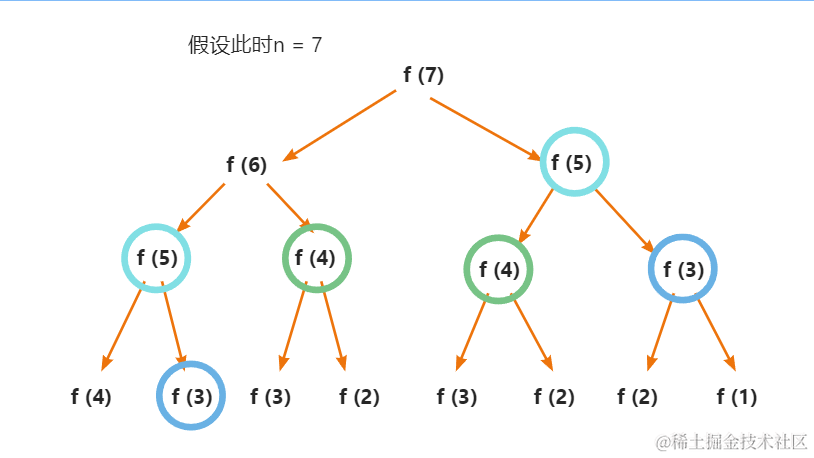
一棵高度为k的决策树形状为二叉树，每个地方都分出两个选择

时间复杂度 2^K

这个版本虽然比较容易想到，符合人类正常尝试思维，但是非常容易超时,从图中可以看出这个版本在求解子问题的时候充斥着大量的重复计算，

这样可以引出 相同的子问题 我们可以把每次计算的结果记录下来因此引出了备忘录法

记忆化搜索，自顶向下的动态规划—备忘录法

相比普通的递归计算，其实在时间复杂度上已经接近常用的动态规划了，也已经可以AC了

这也算是一种自顶向下的动态规划思路

具体的操作

增加一个备忘录数组dp[n+1] 每次先去检查表是否已经计算过，如果计算过直接返回表中的结果，避免重复计算

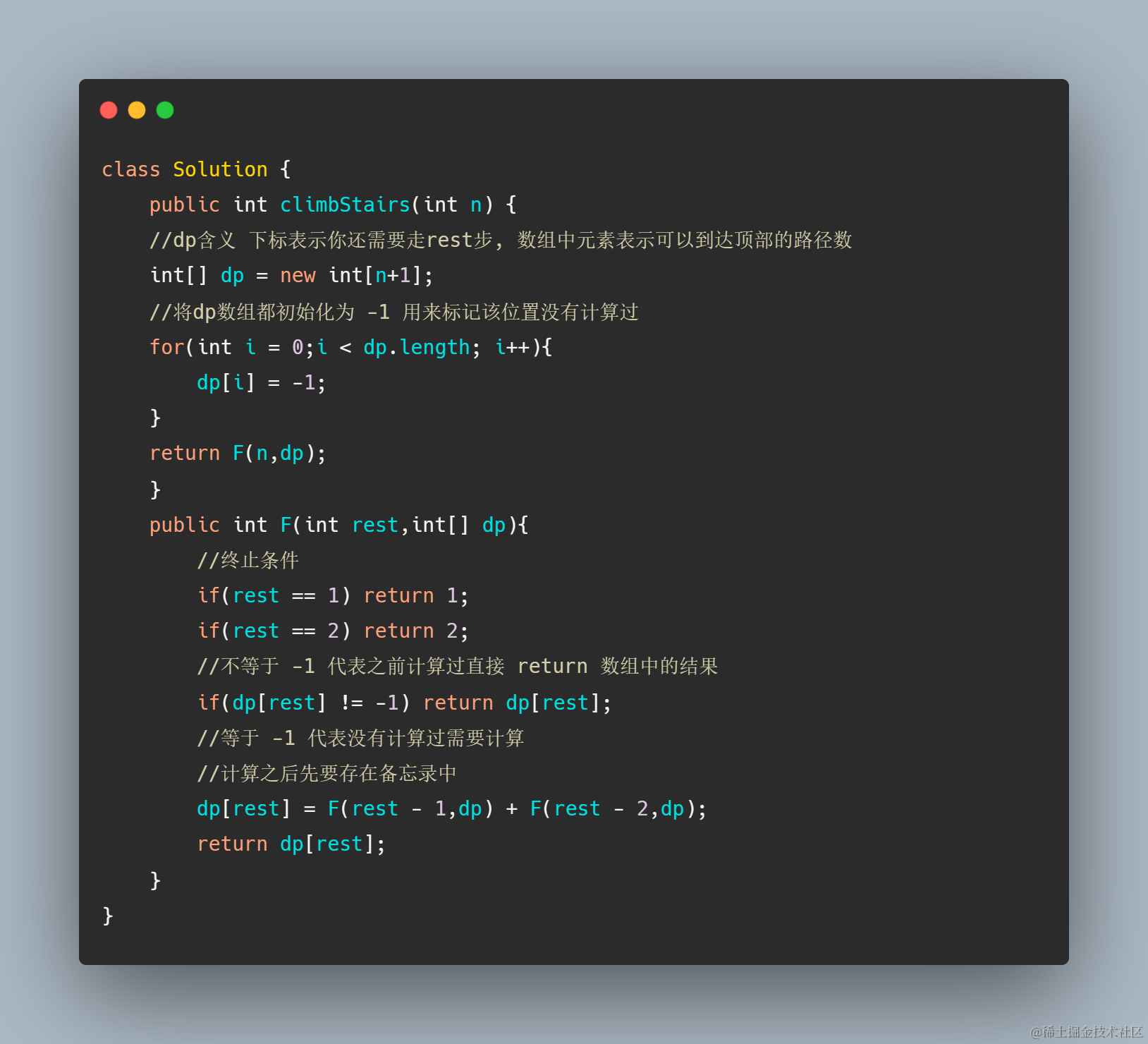
但是该方法还是使用的递归自顶向下的方式计算，而递归会有额外的开销，因此也引出另外一种优化思路，先求解子问题自底向上的求解问题，最后将子问题的解组合起来，

实现的方式就是 通过表数据之间的结构依赖来计算，而这个表结构依赖就是所谓的动态转移方程

自底向上—表结构依赖的动态规划

这一版也需要一个状态记录表，也需要将计算完的结果存到表中 ，和上一般的核心区别在于这里的计算是研究数据之间的表结构依赖关系去计算结果 ，也就是常说的状态转移方程

具体状态转移方程该如何的来呢？ 是你看题直接灵机一现顿悟道法？

动态转移方程的来源 ！！！如果你真的按照本文的思路在思考优化，那么其实动态转移方程也已经从递归的思路中呼之欲出的，动态转移方程就是递归的单层递归逻辑演变而来，

其实基本没有修改，递归版本是将计算结果递归返回给上层的递归调用，然后将这次计算结果记录在备忘录中，而动态规划不过是将结果直接返回到了dp状态表中保存。

在递归备忘录版本中,递归计算完每一个值都会将值记录在dp数组中，假设到最后每一个调用递归的计算需要的数据都保存在了备忘录中，是不是就可以看作只调用表格中的值来计算,用伪代码举个简单的例子

假设求解rest = 5

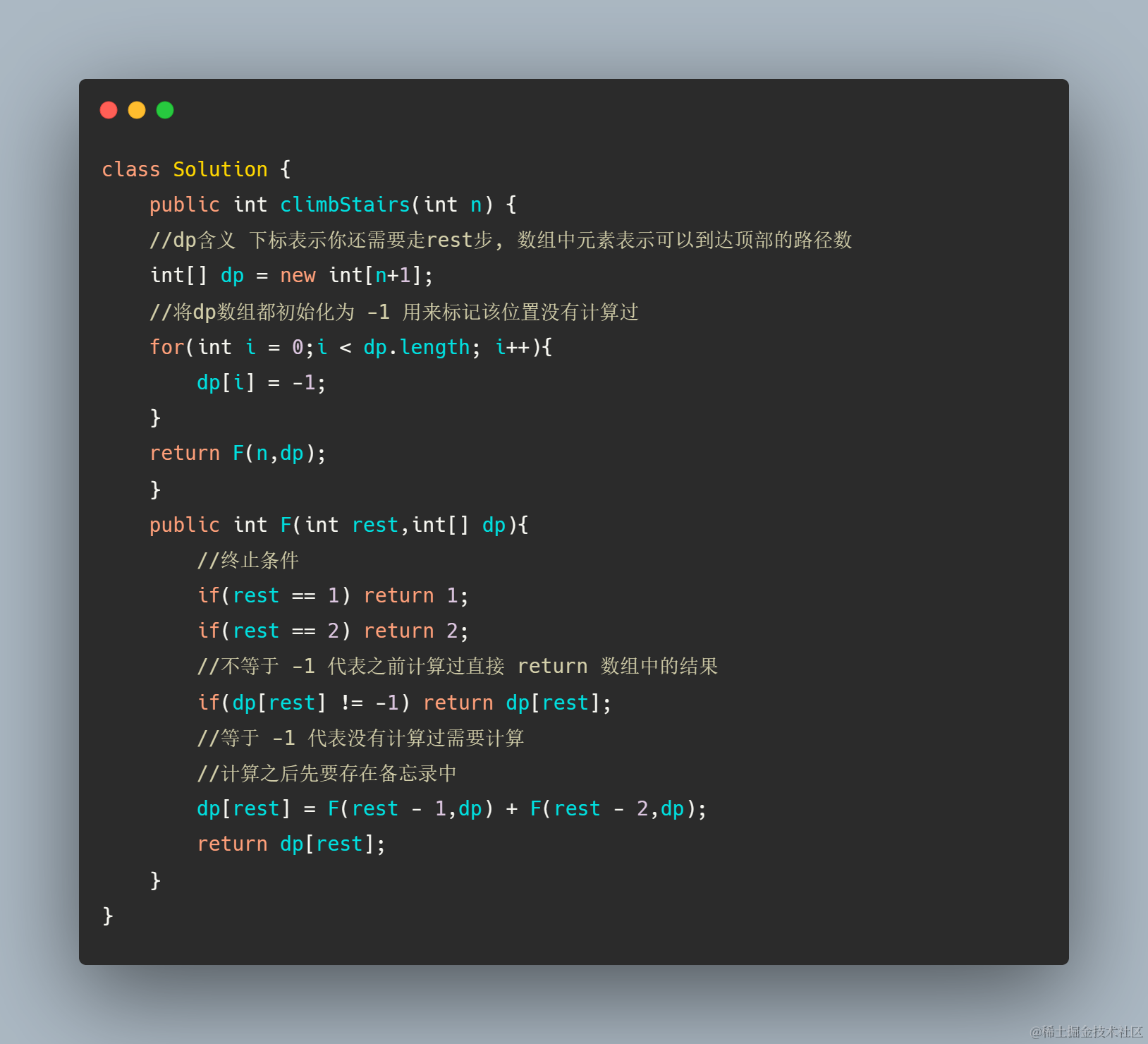
不过其实动态转移方程的本质是通过数据之间的表结构依赖关系去计算

这个表结构依赖关系可以由图表轻松看出,可以轻松得到和理解动态转移方程

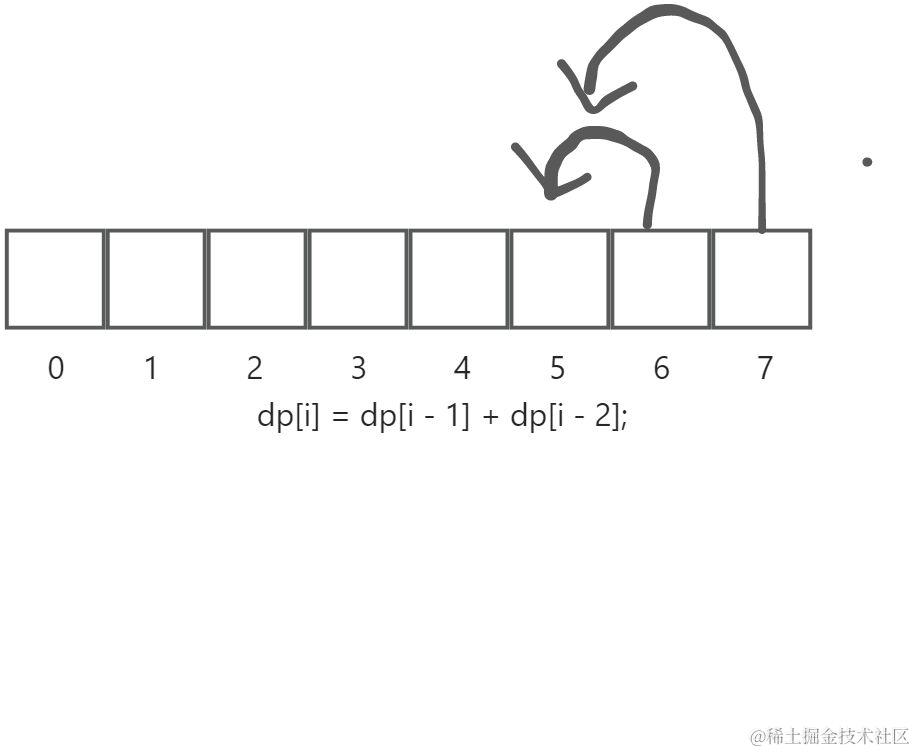
如果你已经会求解动态转移方程，不过这里其实还有一个问题就是递归是自顶向下去计算也就是我们先计算f（7）的时候再去递归计算f（6）和f（5），在最开始的备忘录数组中是没有数据也可以计算的。

但是在通过动态转移方程，只严格依赖表结构的计算，自底向上的计算，也就是我们先计算得到的dp[1] ,dp[2]，再通过方程计算得出dp[3]，因此最开始表中必须要有基础数据。

由此引出动态规划重要步骤之一：dp数组的初始化

很多人有一个误区认为动态规划难点也就一个动态转移方程了，刷题可能看个动态转移方程一抄就觉得自己ok了，如果还是AC不了，可能就一点一点的 欸 ！模仿，读书人的事情怎么能是抄呢

其实还有一部十分的关键就是关于dp数组的初始化，

相信你看到现在也大致猜到了初始化的思路源于递归的终止条件，也就是最基础的初始化数据。也可以从题意中取提取更多初始化的信息丰富dp基础信息;

核心点 ： 递归的终止条件可以作为初始化的关键信息 类似于斐波那契数列的第零项和第一项dp数组初始化的数据， 本题还可以直接读题意获取初始化信息

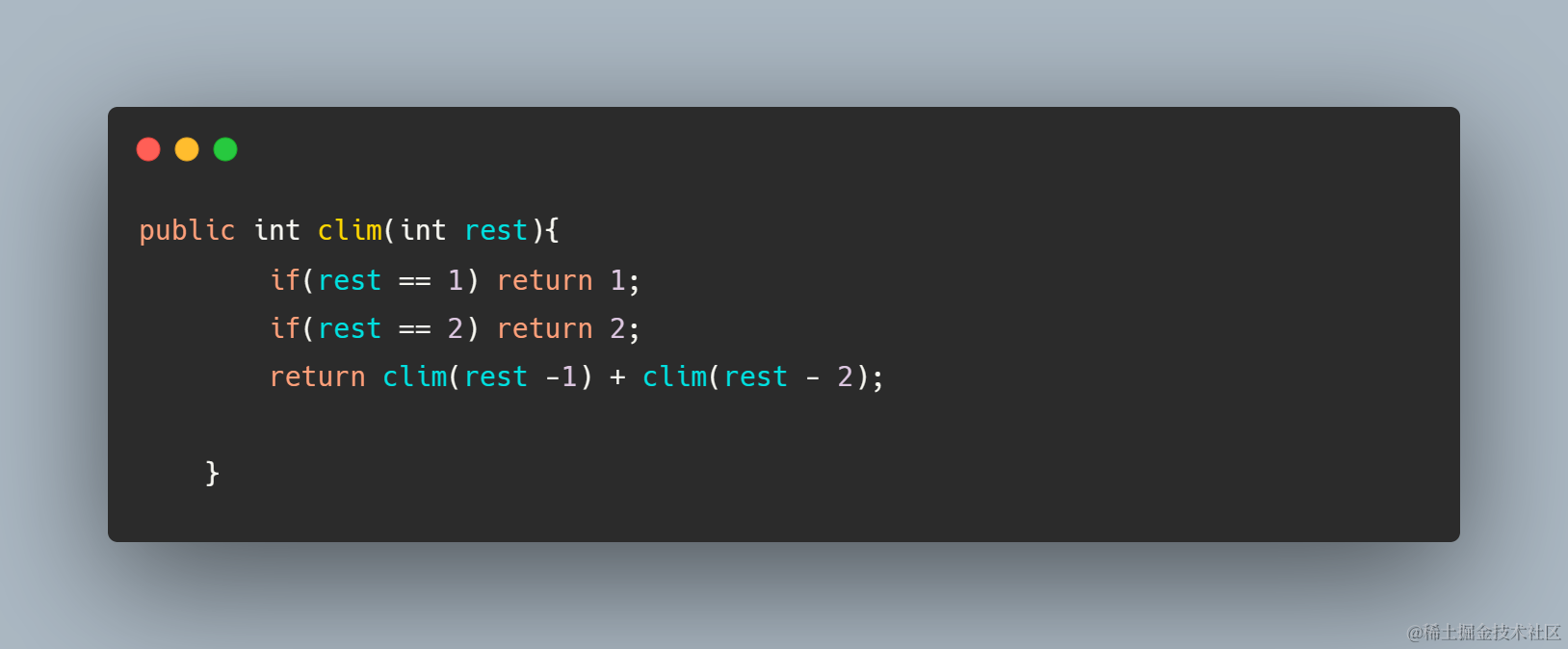
其实这里还有重要的一步就是遍历结算的顺序，遍历起点应该是你可以通过初始化的基础数据的方向开始，dp[0],dp[1],dp[2]有初始化数据，所有从前往后遍历

最后这里放下动态规划版本和初始递归版本的对比

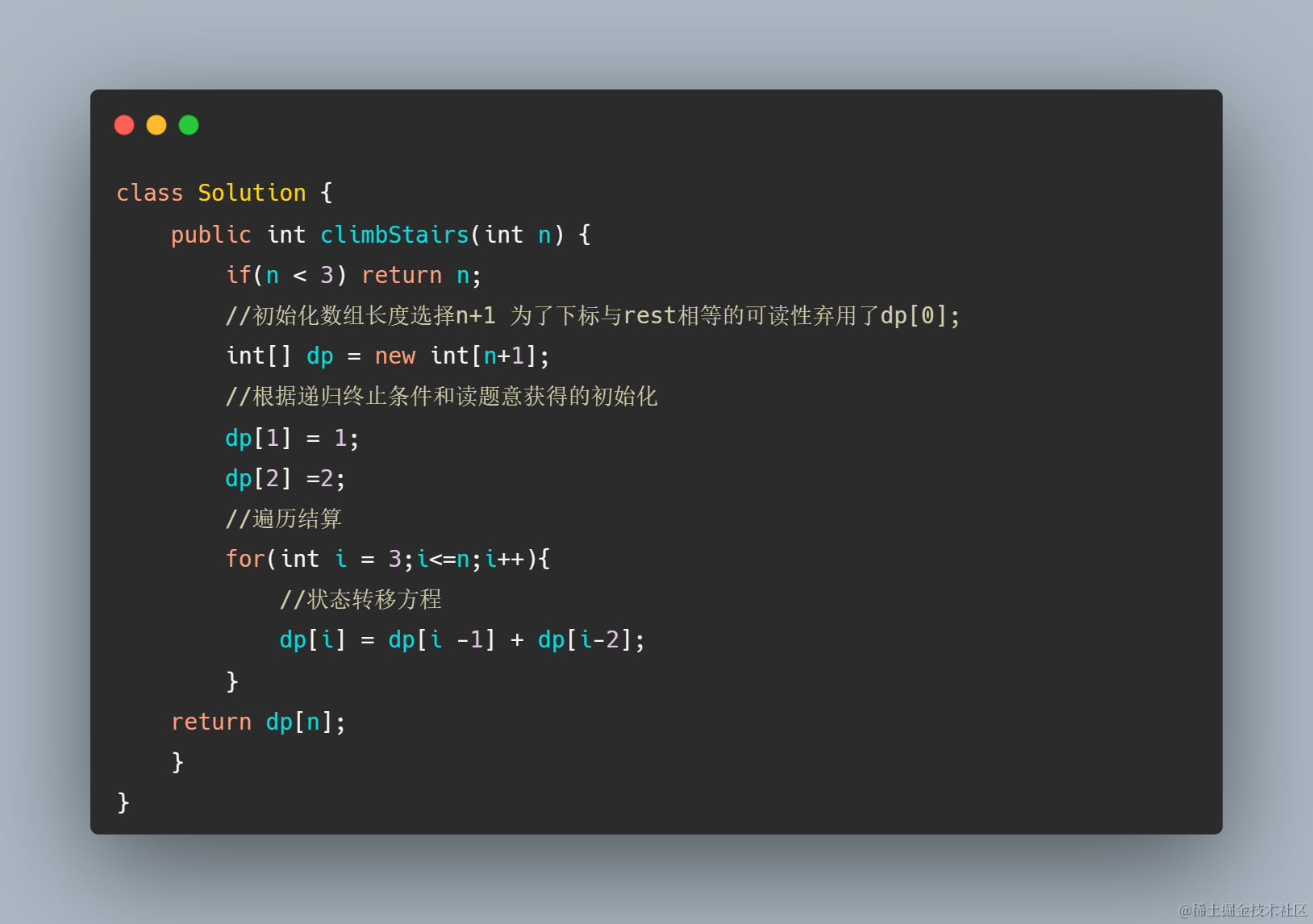
每个格子是通过状态方程计算获取 O(1) ,有n+1格子,时间复杂度为O（n）;

其实到这一步时间复杂度上已经不是优化方向了，更多是考虑如何优化code更加简洁优雅 和一些常数时间的优化， 但是空间复杂度上还可以有更多的优化，

空间上的优化

类似于有类似压缩状态 ，可以使用滚动数组优化 01背包中可以将二维数组优化为一维数组 ，而类似最小花费爬楼梯中，将一维数组优化为 几个状态转移的变量

还有一些常见的动态规划优化例如

有枚举的动态规划 可以通过斜率相加 去优化 枚举，减少枚举次数

还有一些区间范围的dp模型也有优化套路,

这里不展开细说更多了，之后dp的优化套路和常见模型会一起再出一起新的总结 todo

---

小试牛刀—leetcode62.不同路径

力扣链接https://leetcode.cn/problems/unique-paths/

你可以动手 代码放到力扣去运行和提交试试，会发现暴力递归回溯可以通过测试用例，

但是当数据量大的时候就会超时。

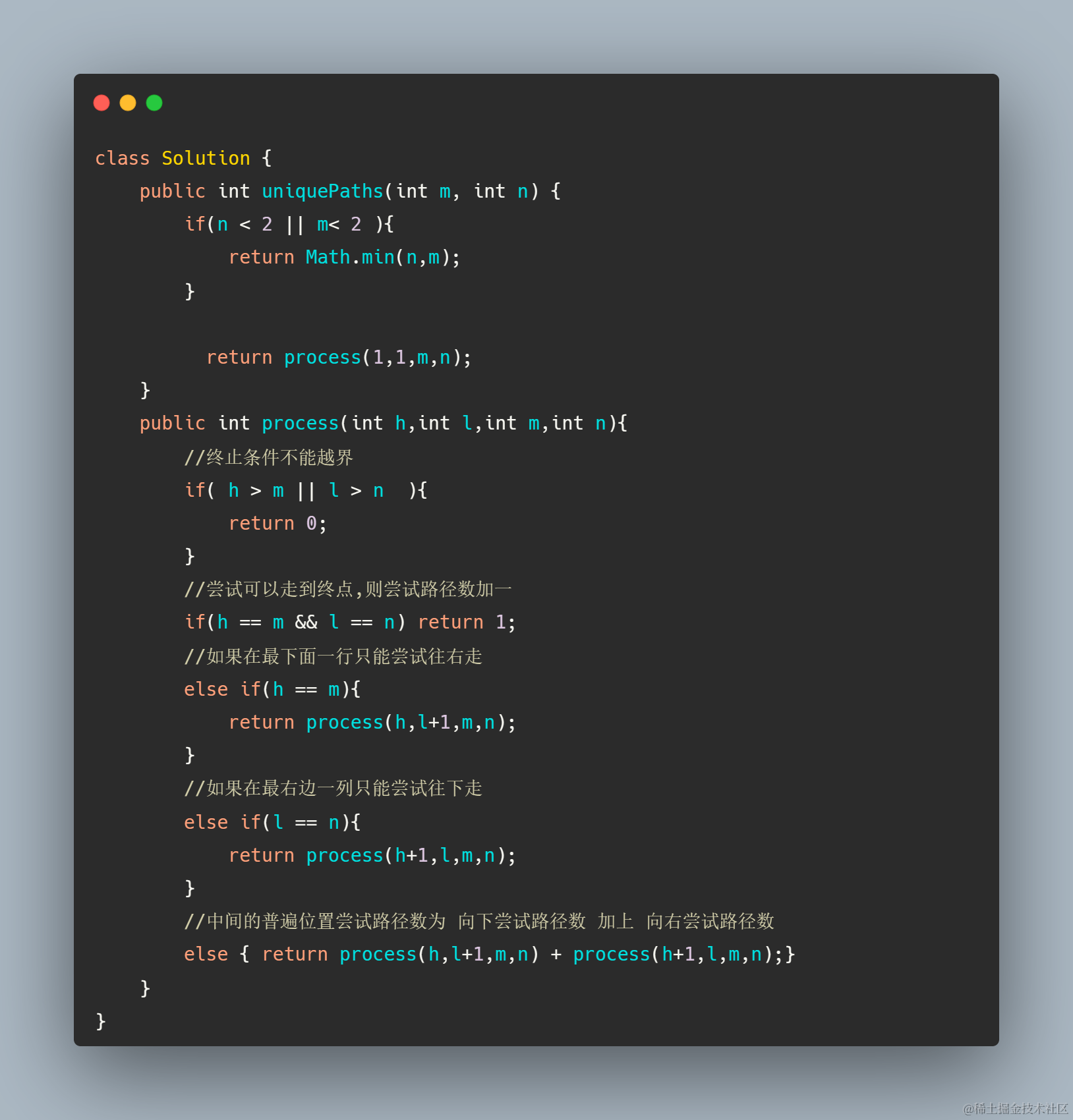
用上备忘录以后你就会发现执行时间大大提升了，和常规的动态规划几乎没有差别1，也可以击败100%了

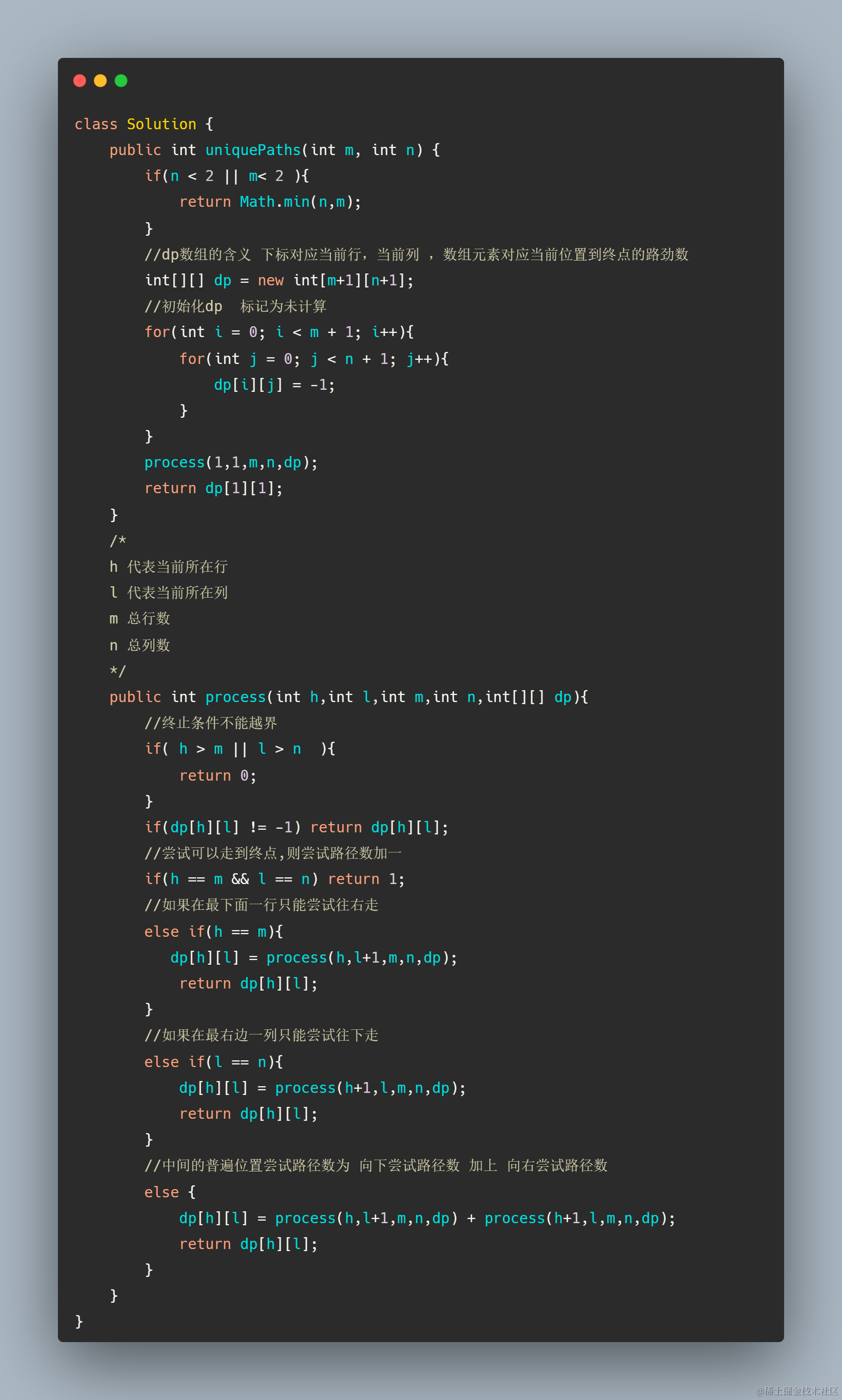
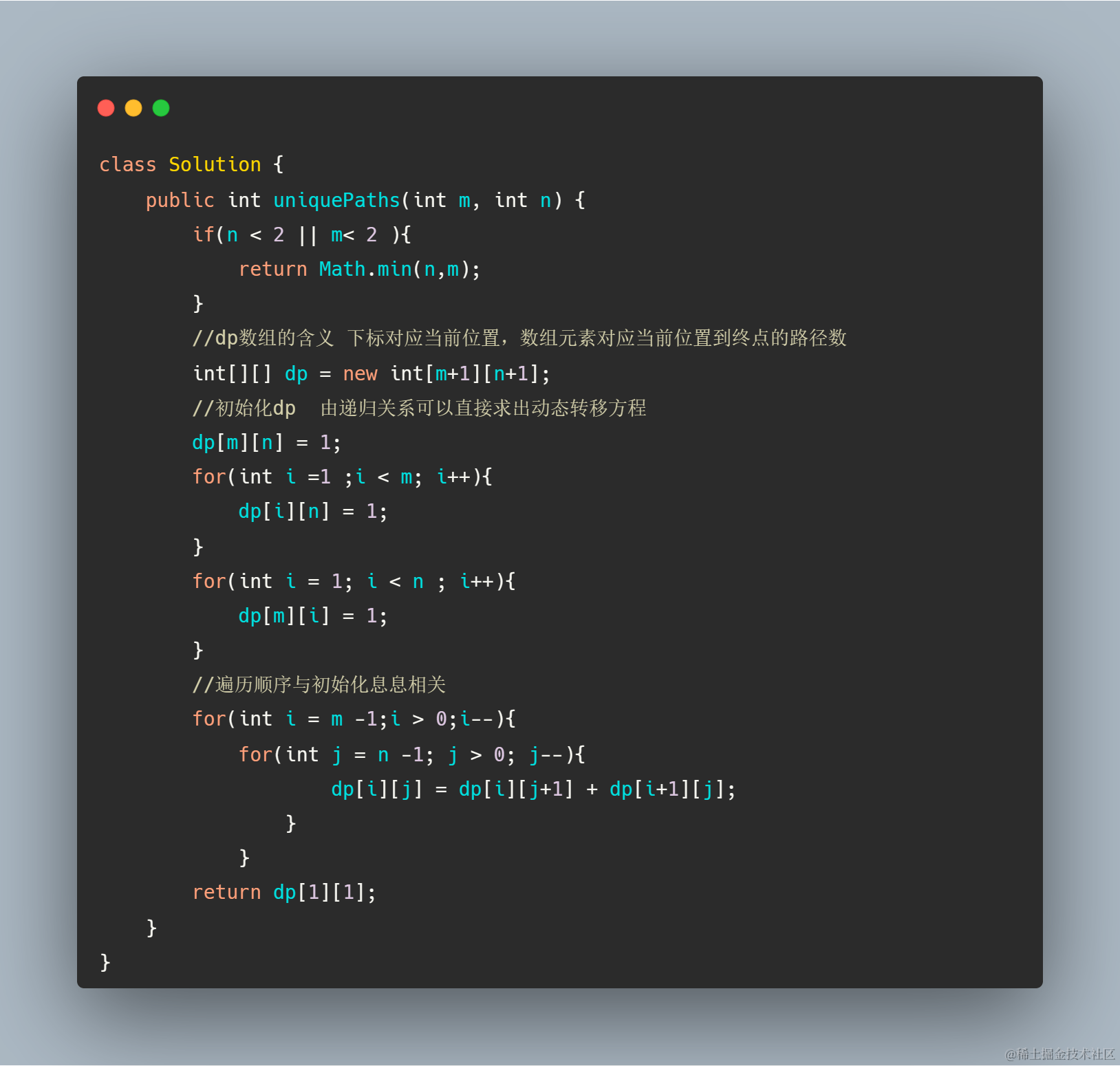
dp数组的含义 下标对应当前位置，数组元素对应当前位置到终点的路径数

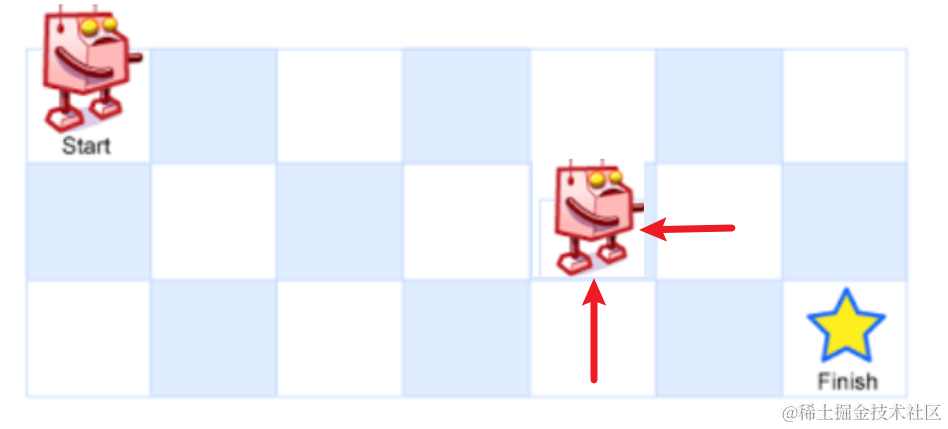
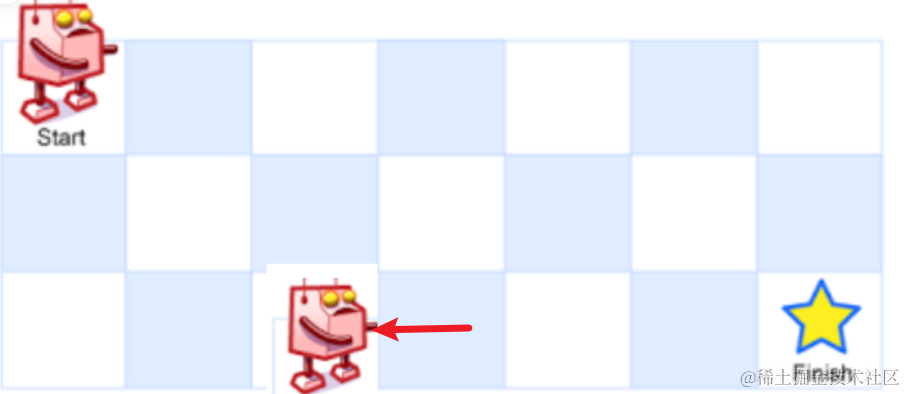
由递归的尝试思想，观察图,对于一般位置来讲每一个格子可以走的路径数为下一步往 右走 和往下走的路径数和

能够得到状态转移方程 dp[i][j] = dp[i][j+1] + dp[i+1][j]

接下来我们考虑一下初始化以及边界条件

1. 如果已经在终点的位置了，将dp[m][n] = 1
2. 如果在最下面一行，只有一直往右边走一种路径 ，或者在最右边一行只有往最下面走一种路径

因此最下面一行和最右边一行都应该初始化为1

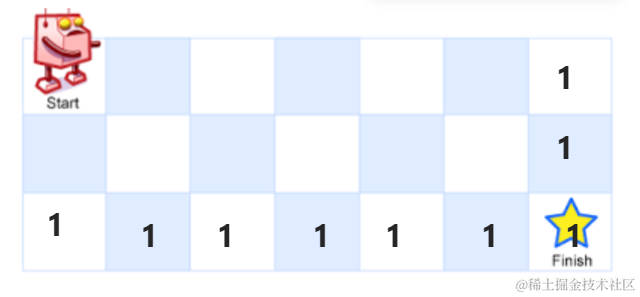
下一步就是遍历顺序了

结合我们的初始化数据和动态转移方程，这题的遍历顺序应该是从最后一排最后一列往第一排第一列遍历。

01背包模型

如果你看完上面的内容已经有所思考那我们就来自己尝试应用在解决背包问题上,

选择背包模型是因为它十分经典，学习规划的第一个遇到的模型基本就是背包模型。

而其实应对大厂面试，背包九讲重点学习 01背包问题和完全背包问题就足够了，其他的背包模型都是竞赛的级别，可以拓展了解但是不是重点

这里的模型是最根本的01背包问题也是最重要的背包模型

题目为：有n件物品和一个最多能背重量为w 的背包。给你一个全部物品重量的数组weight[ ]，第i件物品的重量是weight[i]，物品价值的数组value[ ],得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。

这里都为了偷懒把一些应该是输入的参数，写成了全局的变量

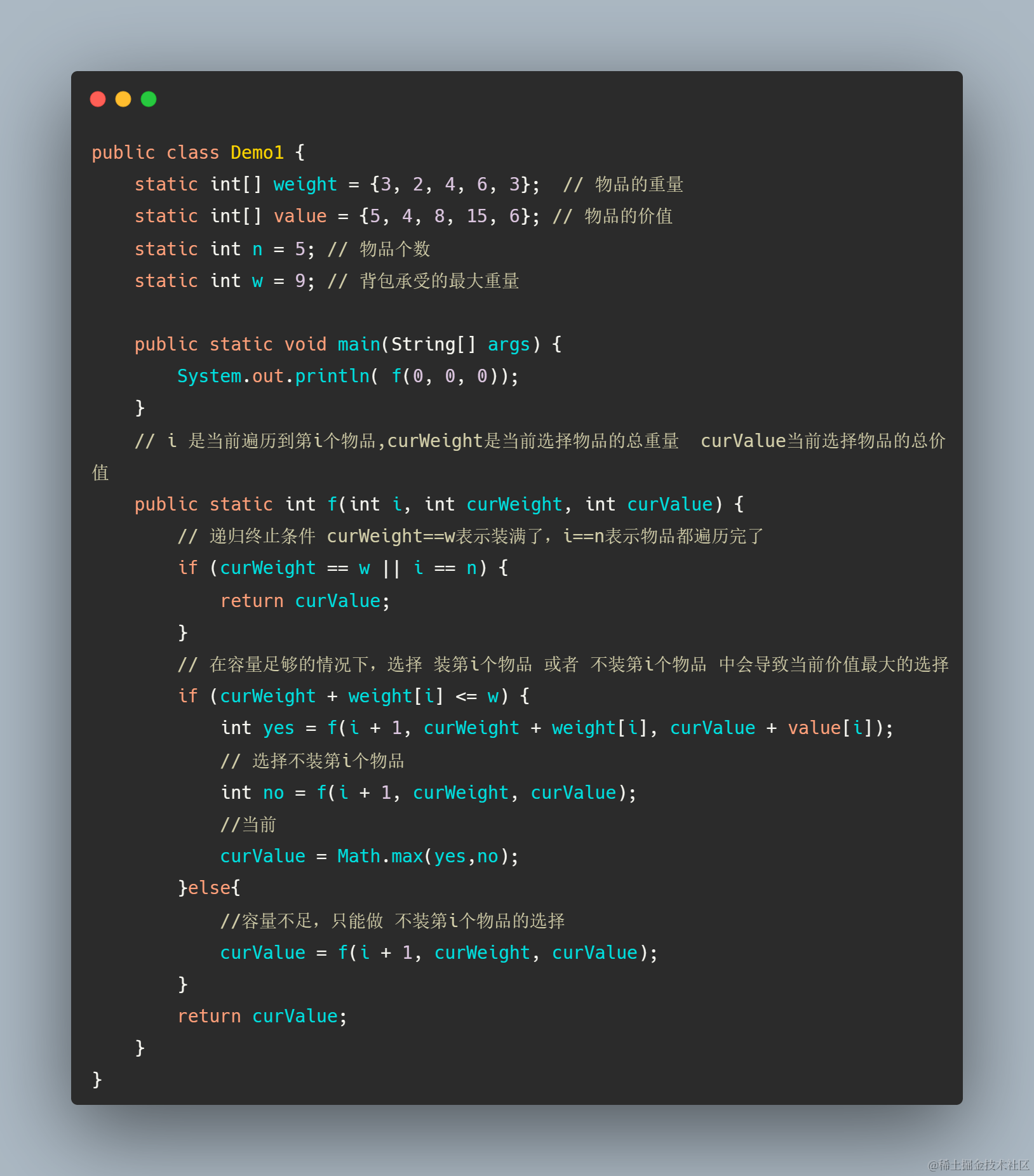
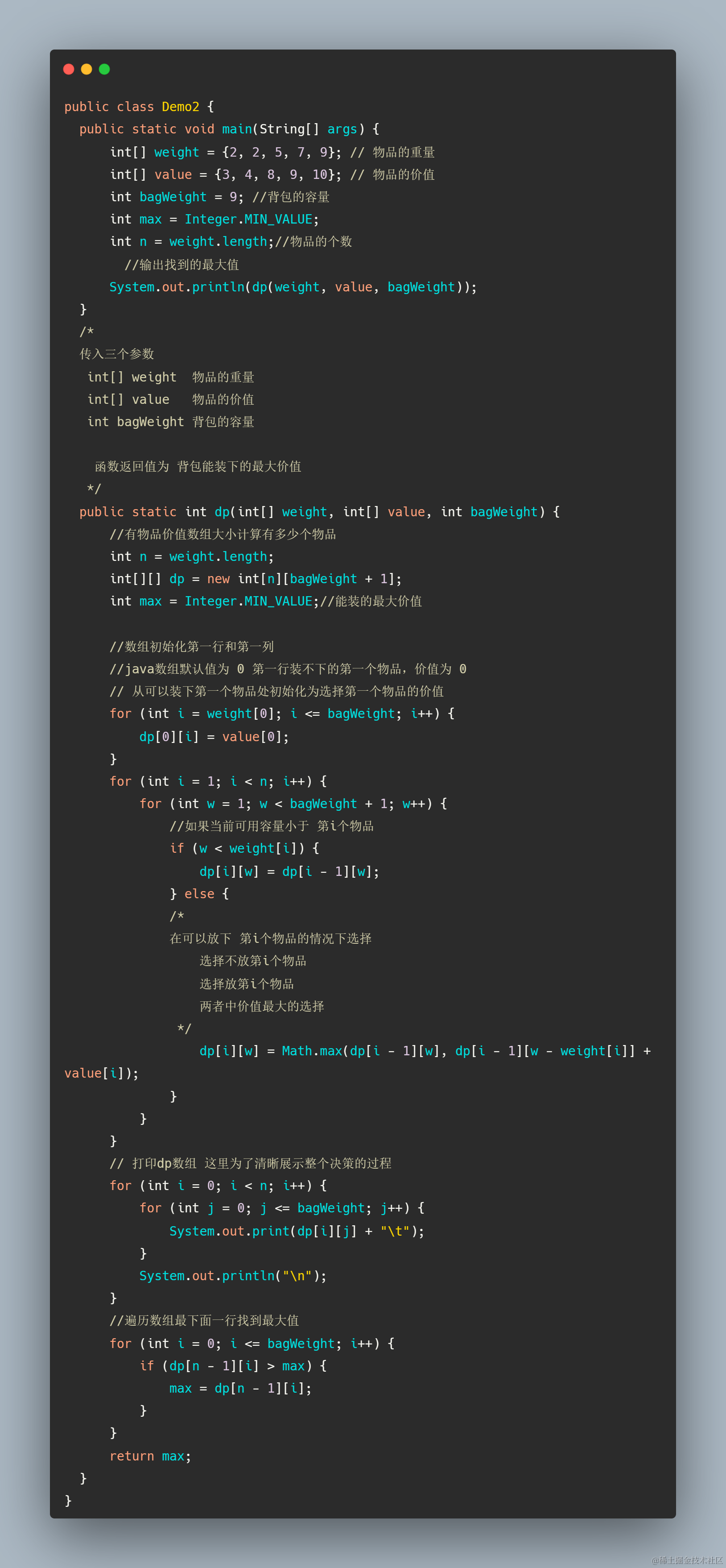
备忘录版本

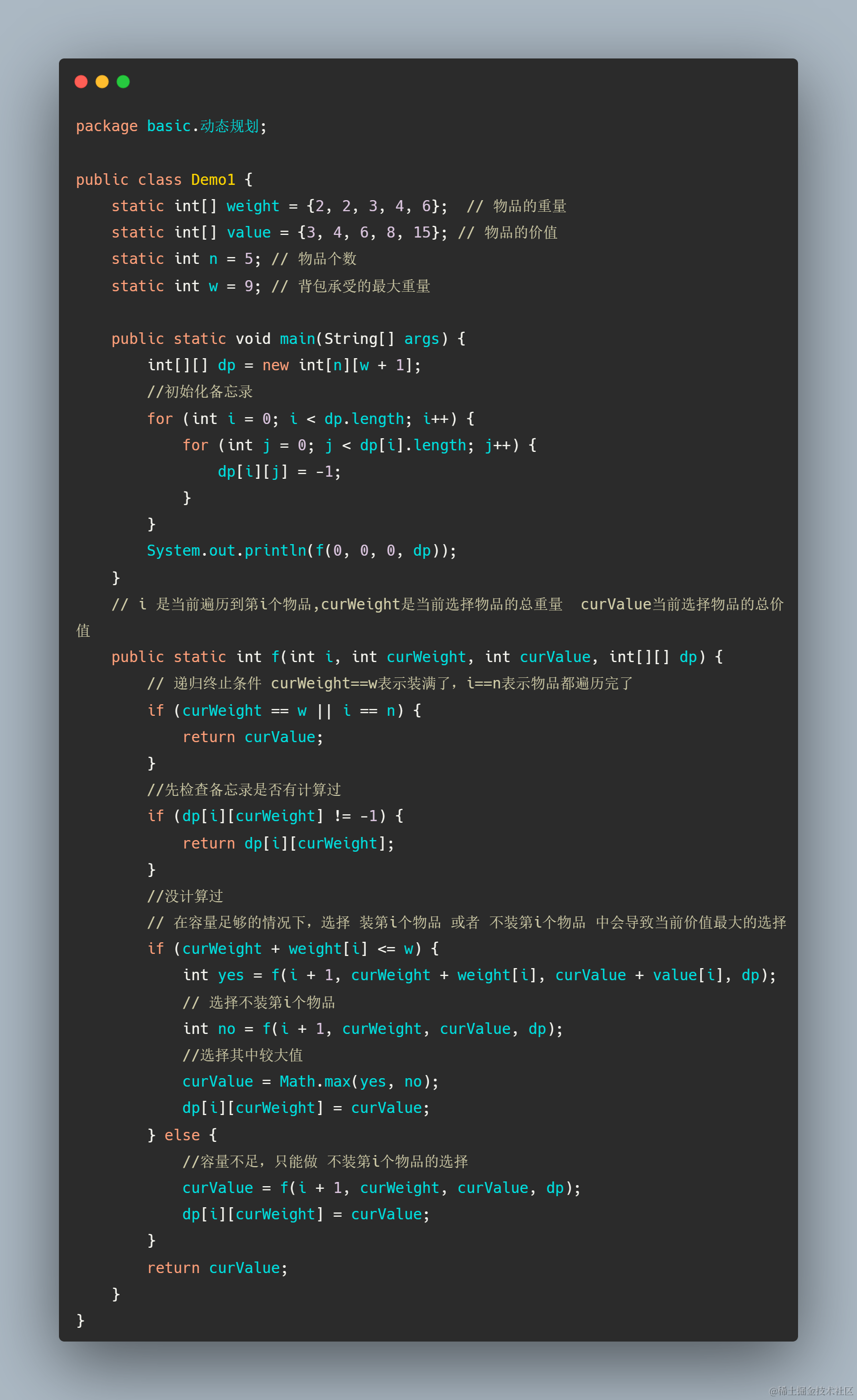
通过这个图能够更加清楚的看出dp数组的一些初始化信息和表结构依赖关系，能够更好的理解动态转移方程，

这里在回忆下动态规划的步骤

• • 1.创建dp 理解其含义
  • 2.递推公式 -状态转移方程
  • 3.初始化dp数组
  • 4.遍历顺序，计算结果

一维dp数组（滚动数组）

对于背包问题其实状态都是可以压缩的。

在使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);

其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上，表达式完全可以是：dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组）。

这就是滚动数组的由来，需要满足的条件是上一层可以重复利用，直接拷贝到当前层。

贪心，分治，回溯，动态规划四种算法思想对比理论性较强

回溯算法是个“万金油”。基本上能用的动态规划、贪心解决的问题，我们都可以用回溯算法解决。回溯算法相当于暴力穷举所有的情况，然后对比得到最优解。不过，回溯算法的时间复杂度非常高，是指数级别的，只能用来解决小规模数据的问题。对于大规模数据的问题，用回溯算法解决的执行效率就很低了。

使用动态规划可以优化时间复杂度，但是并非所有问题都可以使用动态规划，必须满足有最优子结构和重复子问题两个特性才能使用，重复子问题这一点上，动态规划和分治算法的区分非常明显。分治算法要求分割成的子问题，不能有重复子问题，而动态规划正好相反，动态规划之所以高效，就是因为回溯算法实现中存在大量的重复子问题，而动态规划使用状态表记录避免了重复计算.

贪心算法实际上是一种特殊的动态规划,动态规划求解的是全局最优性选择，它解决问题起来更加高效，代码实现也更加简洁。不过，它可以解决的问题也更加有限。它能解决的问题需要满足最优子结构和贪心选择性（这里我们不怎么强调重复子问题）。“贪心选择性”的意思是，通过局部最优的选择，能产生全局的最优选择。每一个阶段，我们都选择当前看起来最优的决策，所有阶段的决策完成之后，最终由这些局部最优解构成全局最优解。

动态规划常见模型

1.线性模型
上述不同路径问题
2.背包模型
零钱兑换系列问题
力扣：
1.https://leetcode.cn/problems/coin-change/description/
2.https://leetcode.cn/problems/coin-change-ii/description/
3.区间DP
例题：最长回文子序列https://leetcode.cn/problems/longest-palindromic-subsequence/description/
4.树形DP
例题： 打家劫舍 |||
力扣连接 ：https://leetcode.cn/problems/house-robber-iii/description/
上司的舞会
5.状态机DP
股票买卖系列题目
1.https://leetcode.cn/problems/best-time-to-buy-and-sell-stock/description/
2.https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-ii/description/
3.https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iii/description/
4.https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-iv/description/
5.含有冷冻期https://leetcode.cn/problems/best-time-to-buy-and-sell-stock-with-cooldown/description/

这篇文章偏向于入门动态规划，这里详细的模型例题展开讲解会再接下来持续更新，点个关注不迷路！

线性模型

线性模型的是动态规划中最常用的模型，上文的不同路径问题就是一个线性的模型，这里的线性指的是状态的排布是呈线性的。【例题1】是一个经典的面试题，我们将它作为线性模型的敲门砖。

**【例题1】**在一个夜黑风高的晚上，有n（n <= 50）个小朋友在桥的这边，现在他们需要过桥，但是由于桥很窄，每次只允许不大于两人通过，他们只有一个手电筒，所以每次过桥的两个人需要把手电筒带回来，i号小朋友过桥的时间为T[i]，两个人过桥的总时间为二者中时间长者。问所有小朋友过桥的总时间最短是多少。

每次过桥的时候最多两个人，如果桥这边还有人，那么还得回来一个人（送手电筒），也就是说N个人过桥的次数为2*N-3（倒推，当桥这边只剩两个人时只需要一次，三个人的情况为来回一次后加上两个人的情况…）。有一个人需要来回跑，将手电筒送回来（也许不是同一个人，realy？！）这个回来的时间是没办法省去的，并且回来的次数也是确定的，为N-2，如果是我，我会选择让跑的最快的人来干这件事情，但是我错了…如果总是跑得最快的人跑回来的话，那么他在每次别人过桥的时候一定得跟过去，于是就变成就是很简单的问题了，花费的总时间：

T = minPTime * (N-2) + (totalSum-minPTime)

来看一组数据 四个人过桥花费的时间分别为 1 2 5 10，按照上面的公式答案是19，但是实际答案应该是17。

具体步骤是这样的：

第一步：1和2过去，花费时间2，然后1回来（花费时间1）；

第二歩：3和4过去，花费时间10，然后2回来（花费时间2）；

第三部：1和2过去，花费时间2，总耗时17。

所以之前的贪心想法是不对的。我们先将所有人按花费时间递增进行排序，假设前i个人过河花费的最少时间为opt[i]，那么考虑前i-1个人过河的情况，即河这边还有1个人，河那边有i-1个人，并且这时候手电筒肯定在对岸，所以opt[i] = opt[i-1] + a[1] + a[i] (让花费时间最少的人把手电筒送过来，然后和第i个人一起过河)如果河这边还有两个人，一个是第i号，另外一个无所谓，河那边有i-2个人，并且手电筒肯定在对岸，所以opt[i] = opt[i-2] + a[1] + a[i] + 2a[2] (让花费时间最少的人把电筒送过来，然后第i个人和另外一个人一起过河，由于花费时间最少的人在这边，所以下一次送手电筒过来的一定是花费次少的，送过来后花费最少的和花费次少的一起过河，解决问题)

所以 opt[i] = min{opt[i-1] + a[1] + a[i] , opt[i-2] + a[1] + a[i] + 2a[2] }

区间模型

区间模型的状态表示一般为d[i][j]，表示区间[i, j]上的最优解，然后通过状态转移计算出[i+1, j]或者[i, j+1]上的最优解，逐步扩大区间的范围，最终求得[1, len]的最优解。

【例题2】给定一个长度为n（n <= 1000）的字符串A，求插入最少多少个字符使得它变成一个回文串。

典型的区间模型，回文串拥有很明显的子结构特征，即当字符串X是一个回文串时，在X两边各添加一个字符’a’后，aXa仍然是一个回文串，我们用d[i][j]来表示A[i…j]这个子串变成回文串所需要添加的最少的字符数，那么对于A[i] == A[j]的情况，很明显有 d[i][j] = d[i+1][j-1] （这里需要明确一点，当i+1 > j-1时也是有意义的，它代表的是空串，空串也是一个回文串，所以这种情况下d[i+1][j-1] = 0）；当A[i] != A[j]时，我们将它变成更小的子问题求解，我们有两种决策：

1、在A[j]后面添加一个字符A[i]；

2、在A[i]前面添加一个字符A[j]；

根据两种决策列出状态转移方程为：

d[i][j] = min{ d[i+1][j], d[i][j-1] } + 1; (每次状态转移，区间长度增加1)

空间复杂度O(n2)，时间复杂度O(n2)， 下文会提到将空间复杂度降为O(n)的优化算法。

背包模型

背包问题是动态规划中一个最典型的问题之一。由于网上有非常详尽的背包讲解，这里只将常用部分抽出来。

**【例题3】**有N种物品（每种物品1件）和一个容量为V的背包。放入第 i 种物品耗费的空间是Ci，得到的价值是Wi。求解将哪些物品装入背包可使价值总和最大。f[i][v]表示前i种物品恰好放入一个容量为v的背包可以获得的最大价值。决策为第i个物品在前i-1个物品放置完毕后，是选择放还是不放，状态转移方程为：

f[i][v] = max{ f[i-1][v], f[i-1][v – Ci] +Wi }

时间复杂度O(VN)，空间复杂度O(VN) （空间复杂度可利用滚动数组进行优化达到O(V) ）

这段模型总结部分先引用一下这位博主的总结，后续我会出新的一期来更加细致的更加完全的DP模型，例题讲解，点个关注不迷路，之后还会系统更新提单

参考资料 《数据结构与算法之美》《代码随想录》
最后的模型三个模型来自https://blog.csdn.net/u013309870/article/details/75193592