有限域的第一种表示方法称为多项式表示,这种表示是基于域的有限 扩张,设p是素数,,只要找到
上一个n次不可约多项式f(x),就 有
。 在信息安全领域,应用最多的有限域是
和素域
。
下面介绍有限域的多项式表示:
选用上的一个n次既约多项式
扩成一个
,由模
的 全体余式的集合,即
每个域的元素都可以表示为一个次数 的多项式.
基本运算操作
举例:
注:以下皆为有限域的运算或有限域上的多项式运算。
1.创建有限域
GF=galois.GF(2**4,repr="poly")repr="poly"指用多项式表示
2.访问有限域的不可约多项式
GF.irreducible_poly3.构建有限域上的多项式
f = galois.Poly([1, 1, 1], field=GF)Out: Poly(x^2 + x + 1, GF(2))
注:在有限域上构建多项式后,几乎任何多项式算术运算都可以 使用 Python 运算符执行,例如f+g、f-g、f*g、加法逆-f、模余f%g、幂f**3.
将多项式和有限域标量相加减乘除,标量被视为 0 次多项式,例:f + GF(3)。
4.函数divmod(f, g):
将一个多项式除以另一个多项式并返回商和余数。
divmod(f, g)5.求多项式最大公因数
d = galois.gcd(f, g)6.扩展的欧几里得除法求多项式最大公因数和逆元
可用该函数求多项式在有限域中的逆元。
d, s, t = galois.egcd(f, g)7.不可约多项式的因式分解
galois.factors(f)
f.factors()以上两种访问方法都可以,galois.factors(f) == f.factors()。
8.访问有限域的属性
print(GF.properties)9.检索有限域的元素
GF7.elements10.输出有限域的算数表(加减乘)
以加法为例:
print(GF.arithmetic_table("+"))11.有限域的生成元
galois.primitive_root(7)#抽象有限域的生成元组
g = GF.primitive_element#具体有限域的最小生成元12.计算有限域 的
的 =
=
有限域的生成元g的定义多项式
叫做本原多项式,设
是
上的n次本原多项式,则使得
的最小正整数
。
g.multiplicative_order()13.输出有限域的生成元表
print(GF.repr_table())实例
求 ![F_{2^{8}}=F_{2}[x]/(x^8+x^4+x^3+x+1)](https://latex.csdn.net/eq?F_%7B2%5E%7B8%7D%7D%3DF_%7B2%7D%5Bx%5D/%28x%5E8+x%5E4+x%5E3+x+1%29) 的生成元
的生成元 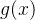 ,并计算
,并计算  ,
,  和所有生成元。
和所有生成元。
import galois
f=galois.irreducible_poly(2,8)
GF=galois.GF(2**8,repr="poly", irreducible_poly=f)
print("f=",f)
g=GF.primitive_element
print("g=",g)
g1=g.multiplicative_order()
print(g1)
print(GF.repr_table(g))输出Out:
......























 731
731

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








