NepCTF2022 招新赛 crypto篇

Paintrain

已于 2022-07-22 22:00:22 修改

阅读量794

点赞数 3

分类专栏：密码文章标签：密码学 ctf python

于 2022-07-21 20:38:18 首次发布

本文链接：https://blog.csdn.net/m0_62506844/article/details/125886853

版权

密码专栏收录该内容

51 篇文章 4 订阅

订阅专栏

动态更新至全部复现完成

文章目录

还是太菜了，看了wp依然是学到了很多，发现nep的密码师傅们经验也太丰富了！

p or s

from secret import keys
from Crypto.Util.number import *
assert(len(keys)==6)
Pbox=[
[0, 3, 6, 9, 10, 11, 13, 16, 18, 19, 20, 24, 25, 27, 28, 29, 30, 31],
[0, 1, 3, 8, 9, 11, 12, 14, 16, 18, 19, 23, 24, 25, 26, 28, 29],
[0, 1, 2, 3, 9, 10, 11, 13, 19, 20, 22, 25, 27, 28, 29, 31],
[0, 2, 3, 5, 6, 7, 8, 13, 16, 19, 21, 25, 26, 27, 28],
[2, 4, 6, 7, 9, 11, 12, 13, 16, 17, 20, 21, 22, 23, 24, 25, 27, 31],
[2, 10, 13, 15, 16, 17, 21, 22, 23, 24, 29, 31],
[1, 2, 8, 11, 12, 13, 16, 17, 19, 21, 22, 24, 25, 26, 27, 28, 30, 31],
[0, 3, 6, 13, 14, 17, 19, 21, 22, 23, 26, 27, 28],
[1, 5, 7, 8, 11, 12, 14, 15, 19, 23, 25, 27, 31],
[0, 2, 3, 6, 7, 8, 9, 10, 11, 12, 16, 18, 19, 22, 23, 24, 25, 26, 27, 28],
[0, 1, 6, 7, 10, 15, 16, 21, 24, 25, 29, 30],
[1, 4, 5, 6, 7, 12, 13, 15, 18, 19, 20, 22, 26, 27, 29, 31],
[0, 3, 5, 8, 9, 17, 21, 22, 24, 25, 26, 27, 30],
[0, 2, 3, 4, 5, 6, 7, 8, 11, 17, 19, 20, 24, 25, 26, 27, 30],
[2, 6, 7, 8, 11, 12, 14, 16, 20, 21, 22, 24, 29, 30, 31],
[0, 2, 5, 6, 7, 8, 9, 10, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 29, 31],
[0, 1, 2, 3, 4, 5, 8, 10, 11, 12, 13, 16, 17, 18, 20, 21, 22, 23, 25, 26, 28, 29, 30],
[3, 5, 6, 8, 10, 13, 14, 17, 19, 20, 21, 22, 24, 26, 27, 29, 30],
[1, 3, 6, 12, 14, 15, 16, 17, 18, 21, 24, 25, 26, 27, 28],
[0, 1, 2, 3, 5, 6, 7, 8, 9, 12, 13, 19, 20, 23, 26, 29, 30],
[3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 20, 21, 22, 25, 26, 27, 28, 29, 30],
[0, 1, 2, 4, 6, 7, 9, 10, 11, 13, 15, 16, 18, 19, 20, 21, 25, 31],
[0, 2, 7, 10, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 29, 31],
[1, 2, 3, 5, 7, 8, 18, 19, 21, 22, 23, 25, 31],
[3, 4, 7, 8, 10, 11, 13, 14, 17, 18, 19, 21, 22, 23, 24, 28, 29],
[0, 2, 6, 7, 8, 10, 11, 12, 13, 16, 18, 19, 21, 23, 31],
[0, 1, 3, 4, 8, 13, 14, 16, 18, 19, 21, 26, 27, 30, 31],
[5, 6, 7, 9, 13, 14, 15, 18, 19, 20, 21, 24, 25, 28],
[1, 3, 4, 5, 6, 7, 11, 14, 16, 17, 19, 20, 21, 22, 23, 25, 30, 31],
[2, 3, 4, 6, 7, 11, 13, 17, 18, 19, 20, 23, 24, 25, 26, 28, 29, 30, 31],
[0, 1, 2, 3, 4, 7, 9, 10, 13, 15, 16, 19, 22, 23, 24, 25, 27],
[0, 1, 3, 4, 12, 16, 18, 19, 26, 30]]

def enc(flag):
    t=flag
    for i in keys:
       q=[]
       for j in Pbox:
           q.append(sum([t[k] for k in j])%2)
       t=[int(q[j])^int(i[j]) for j in range(32)]
    return t
 
assert(len(flag)==32)
fb=bin(bytes_to_long(flag))[2:].zfill(32*8)
ciphertext=""
for i in range(0,len(fb),32):
    t=enc([int(j) for j in fb[i:i+32]])
    ciphertext+="".join([str(j) for j in t])
 
print(ciphertext)
"""
0111110000100101000001101011110111101100000010110011101111000101111110111111100100100010001011000101000110110011111101000001001000000101111000001110001111001001100100111000011011101111111101001011100000100100110011111101100111001100111111110001111011101100

"""

根据加密流程，可以构造等式：
$P(P(P(P(P(Pm+k0)+k1)+k2)+k3)+k4)+k5=m*P^6+\sum P^ik_{5-i}$
已知明文前四个字节 “flag”,和密文，也就是已知一组明密文，利用已知明文攻击，可以求出 $\sum P^ik_{5-i}$
然后对应每一组明密文，就只有m不知道了，套方程求解即可
在当时做此题的时候，发现用了6组key，就没有头绪了，想着怎么也不可能恢复出来key了。现在懂得了列式子的重要性哈哈，题还是做少了。
exp:

from tqdm import tqdm
from Crypto.Util.number import *


c="0111110000100101000001101011110111101100000010110011101111000101111110111111100100100010001011000101000110110011111101000001001000000101111000001110001111001001100100111000011011101111111101001011100000100100110011111101100111001100111111110001111011101100"
cc=[]
for i in range(0,len(c),32):
    cc.append(c[i:i+32])
    
Pbox=[
[0, 3, 6, 9, 10, 11, 13, 16, 18, 19, 20, 24, 25, 27, 28, 29, 30, 31],
[0, 1, 3, 8, 9, 11, 12, 14, 16, 18, 19, 23, 24, 25, 26, 28, 29],
[0, 1, 2, 3, 9, 10, 11, 13, 19, 20, 22, 25, 27, 28, 29, 31],
[0, 2, 3, 5, 6, 7, 8, 13, 16, 19, 21, 25, 26, 27, 28],
[2, 4, 6, 7, 9, 11, 12, 13, 16, 17, 20, 21, 22, 23, 24, 25, 27, 31],
[2, 10, 13, 15, 16, 17, 21, 22, 23, 24, 29, 31],
[1, 2, 8, 11, 12, 13, 16, 17, 19, 21, 22, 24, 25, 26, 27, 28, 30, 31],
[0, 3, 6, 13, 14, 17, 19, 21, 22, 23, 26, 27, 28],
[1, 5, 7, 8, 11, 12, 14, 15, 19, 23, 25, 27, 31],
[0, 2, 3, 6, 7, 8, 9, 10, 11, 12, 16, 18, 19, 22, 23, 24, 25, 26, 27, 28],
[0, 1, 6, 7, 10, 15, 16, 21, 24, 25, 29, 30],
[1, 4, 5, 6, 7, 12, 13, 15, 18, 19, 20, 22, 26, 27, 29, 31],
[0, 3, 5, 8, 9, 17, 21, 22, 24, 25, 26, 27, 30],
[0, 2, 3, 4, 5, 6, 7, 8, 11, 17, 19, 20, 24, 25, 26, 27, 30],
[2, 6, 7, 8, 11, 12, 14, 16, 20, 21, 22, 24, 29, 30, 31],
[0, 2, 5, 6, 7, 8, 9, 10, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 29, 31],
[0, 1, 2, 3, 4, 5, 8, 10, 11, 12, 13, 16, 17, 18, 20, 21, 22, 23, 25, 26, 28, 29, 30],
[3, 5, 6, 8, 10, 13, 14, 17, 19, 20, 21, 22, 24, 26, 27, 29, 30],
[1, 3, 6, 12, 14, 15, 16, 17, 18, 21, 24, 25, 26, 27, 28],
[0, 1, 2, 3, 5, 6, 7, 8, 9, 12, 13, 19, 20, 23, 26, 29, 30],
[3, 4, 6, 7, 8, 9, 10, 11, 12, 13, 14, 16, 20, 21, 22, 25, 26, 27, 28, 29, 30],
[0, 1, 2, 4, 6, 7, 9, 10, 11, 13, 15, 16, 18, 19, 20, 21, 25, 31],
[0, 2, 7, 10, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 25, 29, 31],
[1, 2, 3, 5, 7, 8, 18, 19, 21, 22, 23, 25, 31],
[3, 4, 7, 8, 10, 11, 13, 14, 17, 18, 19, 21, 22, 23, 24, 28, 29],
[0, 2, 6, 7, 8, 10, 11, 12, 13, 16, 18, 19, 21, 23, 31],
[0, 1, 3, 4, 8, 13, 14, 16, 18, 19, 21, 26, 27, 30, 31],
[5, 6, 7, 9, 13, 14, 15, 18, 19, 20, 21, 24, 25, 28],
[1, 3, 4, 5, 6, 7, 11, 14, 16, 17, 19, 20, 21, 22, 23, 25, 30, 31],
[2, 3, 4, 6, 7, 11, 13, 17, 18, 19, 20, 23, 24, 25, 26, 28, 29, 30, 31],
[0, 1, 2, 3, 4, 7, 9, 10, 13, 15, 16, 19, 22, 23, 24, 25, 27],
[0, 1, 3, 4, 12, 16, 18, 19, 26, 30]]

flag=bin(bytes_to_long(b"flag"))[2:].zfill(32)
m=[int(i)for i in flag]
m=matrix(GF(2),1,32,m)
P=Matrix(GF(2),32,32)
j=0
for box in Pbox:
    for i in range(32):
        if i in box:
            P[i,j]=1
    j+=1
c=[int(i)for i in cc[0]]
c=matrix(GF(2),1,32,c)

sum_=c-m*P^6

for c in cc:
    c=[int(i)for i in c]
    c=matrix(GF(2),1,32,c)
    m=(c-sum_)*(P^6)^-1
    m=m.list()
    str_=""
    for i in m:
        str_+=str(i)
    mm=int(str_,2)
    print(long_to_bytes(int(mm)).decode(),end="")
#flag{P_has_no_Semantic_Security}

语义安全，科普一下：
语义安全（英语：Semantic Security）是密码学中的术语。如果已知某段未知文段的密文不会泄露任何该文段的其余信息，那么则称该密文是语义安全的。该概念相似于香农的完善保密性定义。完善保密性意味密文不会泄露任何明文的信息，而语义安全侧重表示被揭露的信息不会被实际窃取。
（源自维基百科。）

中学数学

还是不太擅长做这种题T_T
总体思路就是构造n的等式，q的范围缩小，找到q
我们知道 $q=(1+\frac{1}{2^{500}})p+r\\ n =pq=(1+\frac{1}{2^{500}})p^2+rp$
写到这里应该是基本操作。

先来讲讲 我的思路：

看到 $(1+\frac{1}{2^{500}})p^2+rp$ ，我想到的是 $p^2$ 和rp差距较大，直接对n开2次方应该可以得到p的高位。但是 $(1+\frac{1}{2^{500}})$ 我们没法开方，于是想到左边乘上 $(1+\frac{1}{2^{500}})$ ,这样右边成了
$(1+\frac{1}{2^{500}})^2p^2+(1+\frac{1}{2^{500}})rp$
将 $(1+\frac{1}{2^{500}})n$ 开方，大概能得到 $(1+\frac{1}{2^{500}})p$ 的高位
那么 nextprime( $(1+\frac{1}{2^{500}})p$ )按理应该可以得到q的高位，利用高位攻击恢复q。
我们自己生成几个数来测试一下：
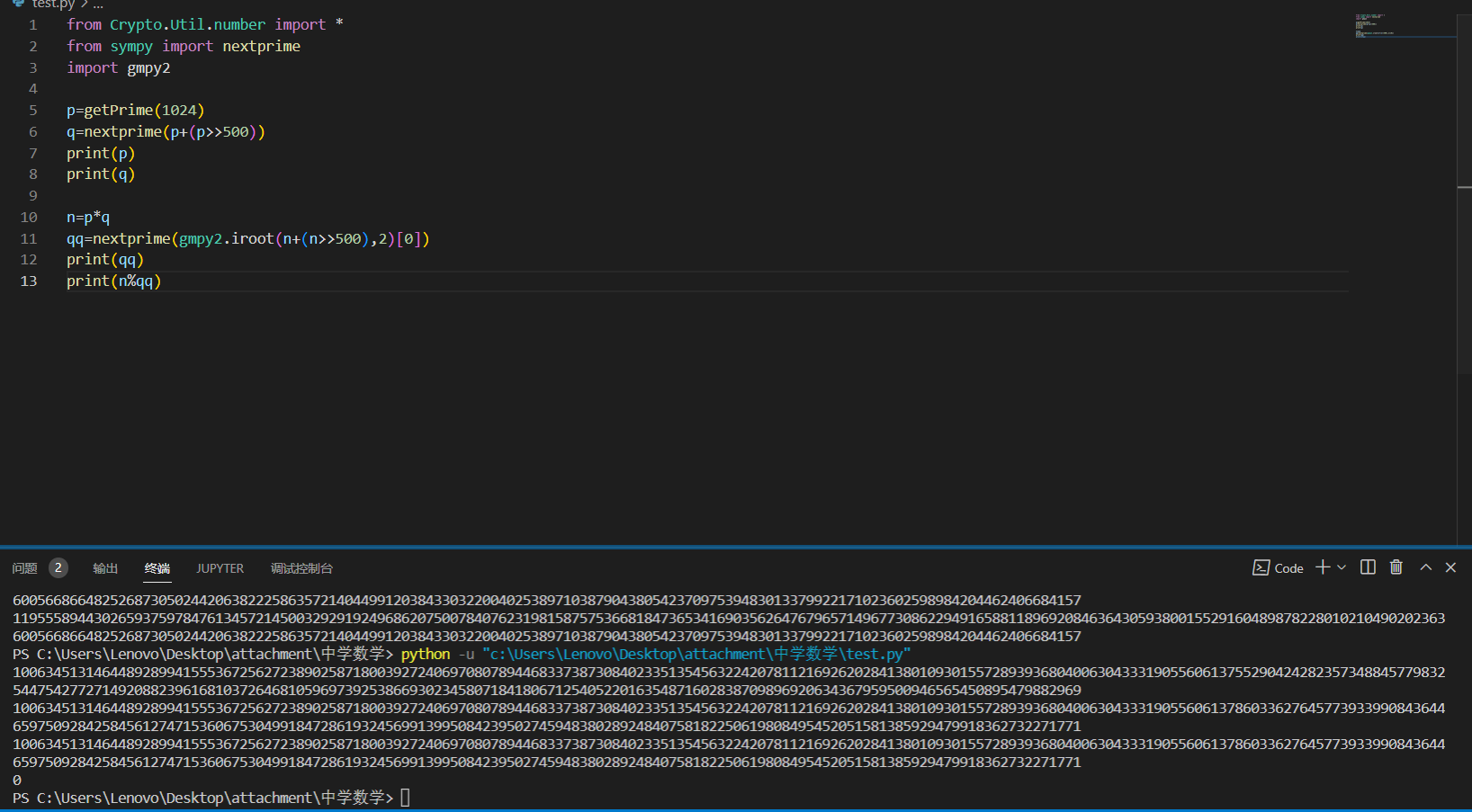
在这里插入图片描述
可以发现直接就能找出来q，连高位攻击都不需要
刚刚的式子是
$(1+\frac{1}{2^{500}})^2p^2+(1+\frac{1}{2^{500}})rp$
可以发现
$(1+\frac{1}{2^{500}})^2p^2的阶数是(1+\frac{1}{2^{500}})rp的两倍$
我们是不是可以推断，至少在1024和2048位的大数上，如果一个数是一个1024位的数和一个2048位的数之和，直接对2048开方有很大概率可以忽略低位的1024位，等同于直接对2048位的大数进行开方呢？这个显然还需要实践不断证明。
利用此方法，写exp：

from Crypto.Util.number import *
from sympy import nextprime
import gmpy2

n= 13776679754786305830793674359562910178503525293501875259698297791987196248336062506951151345232816992904634767521007443634017633687862289928715870204388479258679577315915061740028494078672493226329115247979108035669870651598111762906959057540508657823948600824548819666985698501483261504641066030188603032714383272686110228221709062681957025702835354151145335986966796484545336983392388743498515384930244837403932600464428196236533563039992819408281355416477094656741439388971695931526610641826910750926961557362454734732247864647404836037293509009829775634926600458845832805085222154851310850740227722601054242115507

c= 6253975396639688013947622483271226838902346034187241970785550830715516801386404802832796746428068354515287579293520381463797045055114065533348514688044281004266071342722261719304097175009672596062130939189624163728328429608123325223000160428261082507446604698345173189268359115612698883860396660563679801383563588818099088505120717238037463747828729693649297904035253985982099474025883550074375828799938384533606092448272306356003096283602697757642323962299153853559914553690456801745940925602411053578841756504799815771173679267389055390097241148454899265156705442028845650177138185876173539754631720573266723359186

q=nextprime(gmpy2.iroot(n+(n>>500),2)[0])
p=n//q
phi=(p-1)*(q-1)
d=gmpy2.invert(65537,phi)
m=pow(c,d,n)
print(long_to_bytes(m))

看了下官方wp，理解起来更复杂一点，但是按照他的这个思路，写出来的exp和我的是一模一样的，虽然说做法不一样。

上面我们说到：
$(1+\frac{1}{2^{500}})n =(1+\frac{1}{2^{500}})^2p^2+(1+\frac{1}{2^{500}})rp$
可以得到：
$(1+\frac{1}{2^{500}})n =(1+\frac{1}{2^{500}})^2p^2+(1+\frac{1}{2^{500}})rp>(1+\frac{1}{2^{500}})^2p^2$
又：
$q=(1+\frac{1}{2^{500}})p+r\\ q^2=[(1+\frac{1}{2^{500}})p]^2+r^2+2[(1+\frac{1}{2^{500}})pr]>(1+\frac{1}{2^{500}})n$
所以
$(1+\frac{1}{2^{500}})p<\sqrt{(1+\frac{1}{2^{500}})n}<(1+\frac{1}{2^{500}})p+r$
到这一步了，找q就简单了，wp上点到为止，那我也点到为止。嘿嘿
（其实也没剩什么东西了）

COA_RSA

from Crypto.Util.number import getStrongPrime, inverse, bytes_to_long
from secret import get_e, message, flag


def gen_parameter():
    p = getStrongPrime(1024)
    q = getStrongPrime(1024)
    N = p*q
    phi_N = (p-1) * (q-1)
    e = get_e(N, phi_N)
    d = inverse(e, phi_N)

    print(f"N:{N}\n")
    print(f"e:{e}\n")
    return N, e


def enc(m, e, N):
    return pow(m, e, N)


if __name__ == '__main__':
    assert(len(message) == 18)
    assert(flag == b"NepCTF{" + message + b"}")

    N, e = gen_parameter()
    m = bytes_to_long(message)
    c = enc(m, e, N)

    print(f"c:{c}")

"""
N:21584562909016222405243274981318074723609424537864138818516166296882870952596923388616896100179452902343709246295468740335682613555154383977025156631083258377497353559709636001246215851357586251697339782140616762844466658464225538929007012548727508420837702781524936615164070353418037478517089569783507555024418411710631778073941565485748505472232785028182423960096719453903248061164351629862893495202801853287312265865916733075532360012981688805080299664971109817752216823608878051817158172160419426189481753020154076548471877219325637944601624370884640014467928928695819398270014246851395540617763179525187009648347

e:3083508987002317486463324997331153531944203505409162688359452328126124421799560484088128014311350414620529892327924105762240373365022054853860736661583322625356764794244233714463745121622512321671048540305802394692066665494889362704143858935532501202976814683074990945023438621916862496931012795683358222146303422749958603642494190335211644060403826011553655733835479351434022282429633638548092493767861402690047591624267078125799219896130381280612151738318061042109602694447606410766564110264194828211637692086652912524063147129310052531789754620749834783108524619617738417203269142329494376062347356009094704271801

c:4350922598266339224026193891975078418170168801819772034264767820713898265684630717877568988722980203827973605369872324389093738872638952249759042892387749292013137399168284781320083750172563798340746904451459359268152189983004829803065811628192447436195347501480101582498240174872791092809557067538800318476384792579696811714128502969704568997167132768453189707964546102168532460995624338582249438596921314744866700025932162716723912105789085167524526913197129852605391260182535842364550510703599942313178440055016324692710162447783500265413604087721982116926701740447032328198647967485123967003172122184982695286738
"""

没什么特别的，就是get_e函数没有给出，所以肯定和e的生成有关系。
提示是目标向量长度满足 Minkowski’s bound
不得不惊讶于出这道题师傅的知识储备，感觉自己好菜啊。
根据官方wp:
已知
$\begin{bmatrix} A\\ m \end{bmatrix}$ 满足Minkowski’s bound，有：
$A^{2} + m^2 = ( m^{1-e} \ \text{mod}\ n )^2 + m^2 \leq 2n$
（我不知道怎么出来的但我觉得有些道理）
所以
$1.m^{1-e}~(mod~n)的量级为\sqrt{n}$ ,

画一条分割线，因为从这里开始我就看不懂了！
(刚刚问了一下出题师傅，我发现涉及到了数论的一些基础知识，还是抽空补习一下吧。。）

2.可以猜测出 $1 - e$ 很接近 $m$ 的阶，进而有 $\phi(n)/a - b$ ，其中 $\,|\, \phi(n)$ 并且 $a, b$ 很小.

3. $n // e$ 算出a，对 $b$ 进行穷举。已知 $ \phi(n) = (p-1)(q-1) $ 分解 $n = pq$ 是容易的（中学数学），用 $\pmod{p} = 0$ 来判断当前分解是否正确即可。之后再做常规RSA解密就好了。
(理论出自 NepCTF随缘师傅)

可以，很强，看来学习之路比我想象中的还要长好多。。。
根据这道题可以发现，当
$A=m^{1-e}~mod~n$ 且
$\begin{bmatrix}A\\m\end{bmatrix}$ 是最短向量的时候，可以构造此攻击进行攻击。

# sagemath

from Crypto.Util.number import long_to_bytes

    N = 21584562909016222405243274981318074723609424537864138818516166296882870952596923388616896100179452902343709246295468740335682613555154383977025156631083258377497353559709636001246215851357586251697339782140616762844466658464225538929007012548727508420837702781524936615164070353418037478517089569783507555024418411710631778073941565485748505472232785028182423960096719453903248061164351629862893495202801853287312265865916733075532360012981688805080299664971109817752216823608878051817158172160419426189481753020154076548471877219325637944601624370884640014467928928695819398270014246851395540617763179525187009648347
    e = 3083508987002317486463324997331153531944203505409162688359452328126124421799560484088128014311350414620529892327924105762240373365022054853860736661583322625356764794244233714463745121622512321671048540305802394692066665494889362704143858935532501202976814683074990945023438621916862496931012795683358222146303422749958603642494190335211644060403826011553655733835479351434022282429633638548092493767861402690047591624267078125799219896130381280612151738318061042109602694447606410766564110264194828211637692086652912524063147129310052531789754620749834783108524619617738417203269142329494376062347356009094704271801
    c = 4350922598266339224026193891975078418170168801819772034264767820713898265684630717877568988722980203827973605369872324389093738872638952249759042892387749292013137399168284781320083750172563798340746904451459359268152189983004829803065811628192447436195347501480101582498240174872791092809557067538800318476384792579696811714128502969704568997167132768453189707964546102168532460995624338582249438596921314744866700025932162716723912105789085167524526913197129852605391260182535842364550510703599942313178440055016324692710162447783500265413604087721982116926701740447032328198647967485123967003172122184982695286738

def fact_N(phi, N):
    p_plus_q = N - phi + 1
    p_minus_q = isqrt(p_plus_q ** 2 - 4 * N)
    p = int(p_plus_q + p_minus_q) // 2
    if(N % p) != 0:
        print(f"Current phi is incorrect\n")
        return None
    else:
        print(f"Correct. Find p = {p}")
        q = p_plus_q - p
        print(f"q = {q}.\n")
        return p, q

    
def get_m(c, p, q, N):
    def dec(c, d, N):
        return pow(c, d, N)

    phi_N = (p-1) * (q-1)
    d = pow(e, -1, phi_N)
    return dec(c, d, N)


if __name__ == '__main__':
    a = N // e
    print(f"a = {a}")

    for b in range(20):
        phi = (e + b) * a
        fact = fact_N(phi, N)
        if fact is None:
            continue
        else:
            print(f"b = {b}")
            p, q = fact
            print(f"p = {p}")
            print(f"q = {q}")
            break

    m = get_m(c, p, q, N)
    message = long_to_bytes(m)
    flag = b"NepCTF{" + message + b"}"
    print(flag)

"""
b"NepCTF{N0t_4lw4ys_l4tt1ce}"
"""

回去补数学基础了，明天再去研究那个椭圆曲线的伪随机数发生器了。
————————————————————————————————————————————

芜湖来喽

bd_key

from Crypto.Util.number import long_to_bytes, bytes_to_long, getPrime
from FLAG import flag

"""
 Note: I have modified Dual_EC a little bit.
    It would be EASIER for you to exploit it.
"""
class Dual_EC():
    def __init__(self, s_0=None):
        from Crypto.Util.number import getRandomNBitInteger
       
        # Init curve P-256
        self.p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
        self.n = 115792089210356248762697446949407573529996955224135760342422259061068512044369
        self.b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
        self.curve = EllipticCurve(GF(self.p), [-3, self.b])
        
        # Init P, Q
        self.Qx = 0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296
        self.Qy = 0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5
        self.Q = self.curve(self.Qx, self.Qy)
        self.d = getRandomNBitInteger(256)
        self.P = self.d * self.Q      
        
        # Init state, h_adin
        if s_0 == None:
            self.s_i = int(floor((2^16-1)*random()))
        else:
            self.s_i = s_0
        self.h_adin = 0
        
        self.__leak_par()

        
    def __leak_par(self):
        print(f"curve = {self.curve}")
        print(f"P = {self.P}")
        print(f"d = {self.d}")
        print(f"Q = {self.Q}")

    
    # Output 32bytes now.          
    def __Dual_EC_DRBG(self, h_adin = 0): 
        t_i = self.s_i ^^ h_adin
        self.s_i = (t_i*self.P)[0].lift()
        r_i = (self.s_i*self.Q)[0].lift()
        return r_i

    
    def getRandomNBytes(self, N:int) -> bytes:
        result = 0
        req = (N/32).ceil()

        for i in range(req):
            if(i == 0):
                result = (result << (32*8)) | self.__Dual_EC_DRBG(self.h_adin)
            else:
                result = (result << (32*8)) | self.__Dual_EC_DRBG()

        self.s_i = (self.s_i * self.P)[0].lift()

        result = result >> ((32*req - N)*8)
        return long_to_bytes(result)

    
def encrypt_flag(key:bytes) -> bytes:
    from Crypto.Cipher import AES
    from Crypto.Util.Padding import pad
    from FLAG3 import flag
    
    cipher = AES.new(key, AES.MODE_ECB)
    flag_pad = pad(flag, 16)
    ct = cipher.encrypt(flag_pad)
    return ct


def do_schnorr_identification(dbrg):
    p = getPrime(256)
    Zp = Zmod(p)
    g = Zp(2)
    q = g.multiplicative_order()
    Zq = Zmod(q)
    k = 10
    
    
    class SchnorrProver(object):
        def __init__(self):
            self.secret_key = Zq.random_element()
            self.public_key = g^self.secret_key

        def commit(self):
            self.r = Zq.random_element()
            return g^self.r

        def respond(self, challenge):
            return self.r - challenge*self.secret_key

        
    class SchnorrVerifier(object):
        def __init__(self, prover_public_key):
            self.prover_public_key = prover_public_key

        def challenge(self, commitment):
            self.commitment = commitment
            while True:
                c = bytes_to_long(dbrg.getRandomNBytes(32))
                if c < p:
                    break
            self.challenge_number = c
            return self.challenge_number

        def check(self, response):
            check_value = g^response*self.prover_public_key^self.challenge_number
            return self.commitment == check_value

        
    def run_protocol(iterations=1):
        for _ in range(iterations):
            prover = SchnorrProver()
            verifier = SchnorrVerifier(prover.public_key)
            t = prover.commit()
            c = verifier.challenge(t)
            s = prover.respond(c)
            assert(verifier.check(s))
            
            print(f"c = {c}")
            
    run_protocol()
    
    
def main():
    dbrg = Dual_EC()
    do_schnorr_identification(dbrg)
    key = dbrg.getRandomNBytes(16)
    ct = encrypt_flag(key)
    print(f"ct = {bytes_to_long(ct)}")

main()

output:
# curve = Elliptic Curve defined by y^2 = x^3 + 115792089210356248762697446949407573530086143415290314195533631308867097853948*x + 41058363725152142129326129780047268409114441015993725554835256314039467401291 over Finite Field of size 115792089210356248762697446949407573530086143415290314195533631308867097853951
# P = (72696788778535848020209987825324097844942627382508830211685965810687985426258 : 49180397040468497821240854375656422791216946832858522054245540263375986110762 : 1)
# d = 66604141534275704476445937214374130642068729921454877238730830814793201802544
# Q = (48439561293906451759052585252797914202762949526041747995844080717082404635286 : 36134250956749795798585127919587881956611106672985015071877198253568414405109 : 1)
# c = 59100197418944667413449341413044666843726352095054393072750502893110293231642
# ct = 25645992443585671366815910836517434170297823176311632150463962979581372384075859802765045877741181123347569267185176

考察Dual_EC的后门，先看伪随机数发生的原理：
在这里插入图片描述
s0和adin0异或得到t0，t0P的x坐标作为s1。
产生随机数 s1Q的x坐标即为随机数
若继续生成随机数，s1与adin1异或得到t1，t1P的x坐标作为s2，继续依照上述方式依次生成后续随机数。
攻击：
论文：https://eprint.iacr.org/2015/767.pdf

根据论文中描述，假设我们知道P、d、Q和由这个随机数随机生成的r1，那么我们可以知道r1是椭圆曲线上的一个x坐标，根据此x坐标来计算出y坐标，记此x、y坐标为点R，计算dR，那么dR的X坐标即为s1P的X坐标，如此一来，我们就可以恢复所有随机数了！
看这一段代码：

    def __Dual_EC_DRBG(self, h_adin = 0): 
        t_i = self.s_i ^^ h_adin
        self.s_i = (t_i*self.P)[0].lift()
        r_i = (self.s_i*self.Q)[0].lift()
        return r_i

在本题中，adin默认为0，根据异或性质，可以忽略adin
可以发现，题目中先生成了一个c，然后再生成的key，也就是说key应该是生成的第二个随机数。
给了d相当于给了后门。根据上述内容构造exp:

借鉴一下官方wp，按照我的理解修改一下名字
# sagemath

from Crypto.Util.number import long_to_bytes
from Crypto.Cipher import AES

p = 115792089210356248762697446949407573530086143415290314195533631308867097853951
n = 115792089210356248762697446949407573529996955224135760342422259061068512044369
b = 0x5ac635d8aa3a93e7b3ebbd55769886bc651d06b0cc53b0f63bce3c3e27d2604b
E = EllipticCurve(GF(p), [-3, b])
Qx = 0x6b17d1f2e12c4247f8bce6e563a440f277037d812deb33a0f4a13945d898c296
Qy = 0x4fe342e2fe1a7f9b8ee7eb4a7c0f9e162bce33576b315ececbb6406837bf51f5
Q = E(Qx, Qy)
d = 66604141534275704476445937214374130642068729921454877238730830814793201802544
P = d * Q
c = 59100197418944667413449341413044666843726352095054393072750502893110293231642
ct = 25645992443585671366815910836517434170297823176311632150463962979581372384075859802765045877741181123347569267185176


def dec_flag(ct, key):
    cipher = AES.new(key, AES.MODE_ECB)
    ct = long_to_bytes(ct)
    flag = cipher.decrypt(ct)
    print(f"flag = {flag}")
    if b"NepCTF{" in flag:
        print("Success!")
    

def main():
    assert E.is_x_coord(c)
    s1_Q = E.lift_x(c)
    s1_P_x = Integer( (d * s1_Q)[0] )
    s2 = Integer( (s1_P_x * P)[0] )
    r2 = int( (s2 * Q)[0] )
    
    k = r2 >> ((32 - 16) * 8)#key是16位
    key = long_to_bytes(k)
    dec_flag(ct, key)
    
main()

Paintrain

关注

3
点赞
踩
1

收藏

觉得还不错? 一键收藏
打赏
0
评论
NepCTF2022 招新赛 crypto篇

动态更新至全部复现完成还是太菜了，看了wp依然是学到了很多，发现nep的密码师傅们经验也太丰富了！根据加密流程，可以构造等式：P(P(P(P(P(Pm+k0)+k1)+k2)+k3)+k4)+k5=m∗P6+∑Pik5−iP(P(P(P(P(Pm+k0)+k1)+k2)+k3)+k4)+k5=m*P^6+\sum P^ik_{5-i}P(P(P(P(P(Pm+k0)+k1)+k2)+k3)+k4)+k5=m∗P6+∑Pik5−i已知明文前四个字节 “flag”,和密文，也就是已知一组明密文，利用已知
复制链接

扫一扫