本文详细介绍了图的概念、分类（无向图、有向图、环形图、无环图、连通性和强连通性）、顶点度和边的度量，以及五种图的存储结构：邻接矩阵、边集数组、邻接表、链式前向星和哈希表实现的邻接表。
本系列是算法通关手册LeeCode的学习笔记
算法通关手册（LeetCode） | 算法通关手册（LeetCode） (itcharge.cn)
目录
一，图（Graph）
由顶点的非空有限集合 V （由 n > 0 个顶点组成）与边的集合 E （顶点之间的关系）构成的结构。其形式化定义为 G = ( V, E )。
顶点（Vertex）：图中的数据元素通常称为顶点；
边（Edge）：图中两个数据元素之间的关联关系称为边，边的形式化定义为 e = <u, v>，表示从 u 到 v 的一条边，其中 u 称为起始点，v 称为终止点。
子图（Sub Graph），边是子集并且顶点也是子集：
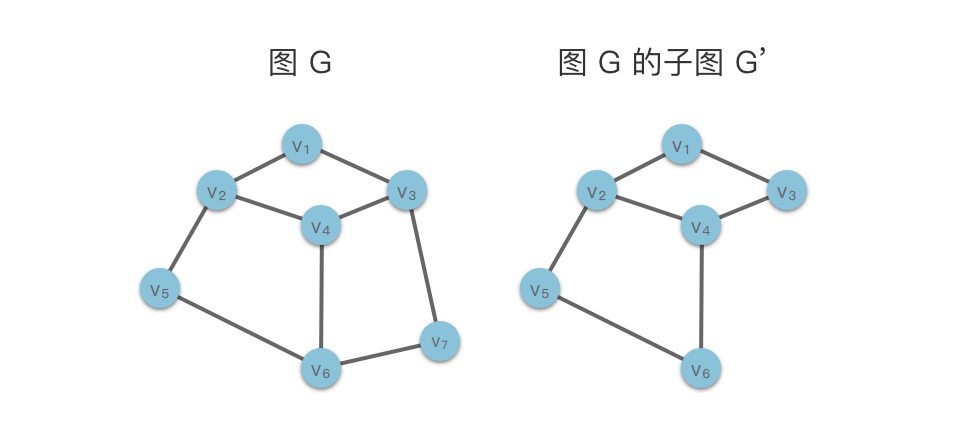
根据定义，G 也是其自身的子图。
图的分类
按照边是否右方向，可以分为 无向图 和 有向图。
无向图（Undirected Graph）：图中的每条边都没有指向性；
有向图（Directed Graph）：图中的每条边都具有指向性。
无向图中，每条边都是由两个顶点组成的无序对，上图中记为(v1, v2) 或 (v2, v1)
有向图中，有向边也被称为弧，是有序对，上图中记为 <v1, v2>。
如果无向图中有 n 个顶点，则无向图中最多有 n * (n - 1) / 2 条边，称这样的无向图为【完全无向图（Completed Undirected Graph）】。
如果有向图中有 n 个顶点，则有向图中最多有 n * （n - 1）条弧，称这样的有向图为 【完全有向图（Completed Directed Graph）】。
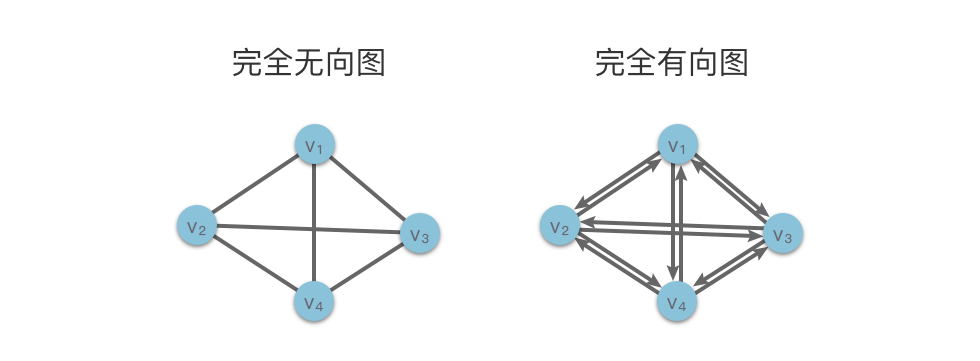
顶点的度
与该顶点 vi 相关联的边的条数，记为 TD(vi)。
例如上图左侧的无向完全图中，顶点 v3 的度为 3.
而对于有向图，可以将顶点的度分为【顶点的出度】和【顶点的入度】
顶点的出度：以该顶点 vi 为出发点的边的条数，记为 OD(vi)；
顶点的入度：以该顶点 vi 为终止点的边的条数，记为 ID(vi)；
有向图中某顶点的度：
TD(vi) = OD(vi) + ID(vi)
环形图和无环图
【路径】是图中的一个重要的概念，简单来说，如果顶点 v[n] 可以通过系列的顶点和边，到达顶点 v[m] ，则称两顶点之间有一条路径，其中经过的顶点序列，称为两个顶点之间的路径。
环（Circle）：如果一条路径的起始点和终止点相同，则称这条路径为【回路】或【环】；
简单路径：顶点序列中，不重复出现某一顶点的路径；
根据图中是否有环，我们可以将图分为【环形图】和【无环图】；
环形图（Circular Graph）：图中存在至少一条环路；
无环图（Acyclic Graph）：图中不存在环路。
特别的，在有向图中，如果不存在环路，则将该图称为【有向无环图（Directed Acyclic Graph）】，缩写为DAG，因为有向无环图拥有特殊的拓扑结构，经常被用于处理动态规划、导航中最短路径、数据压缩等多中算法场景。
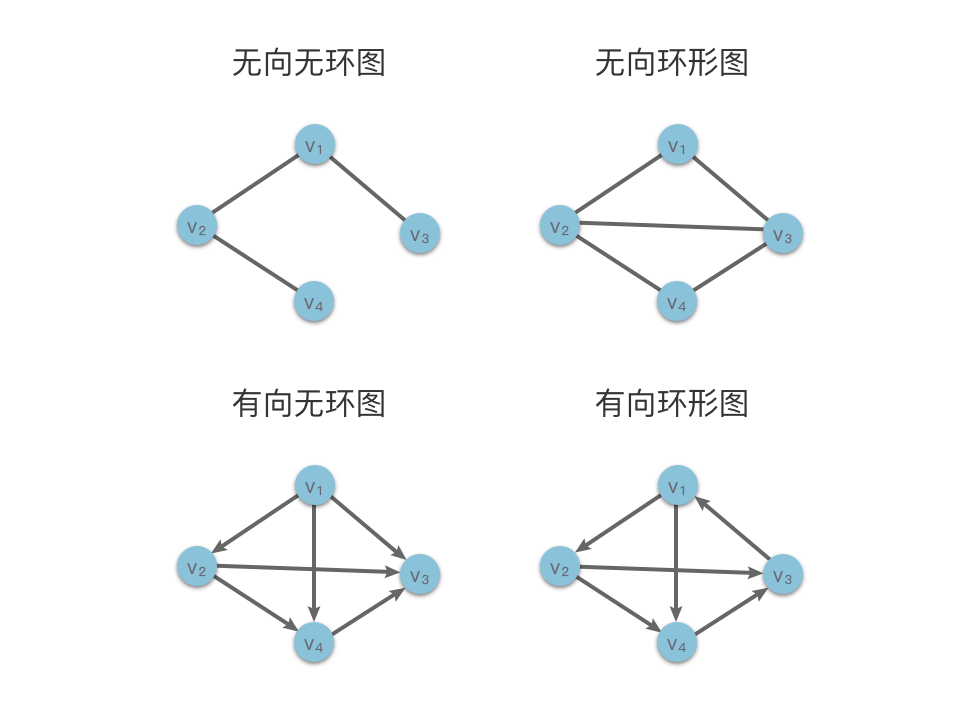
连通图和非连通图
无向图中，如果从顶点 vi 到顶点 vj 有路径，则称顶点 vi 和 vj 是连通的。
连通无向图：在无向图中，图中任意两个顶点之间都是连通的；
非连通无向图：无向图中，至少存在一对顶点之间不存在任何路径；
连通分量：有些无向图可能不是连通图，但是其子图可能是连通的，这些子图称为原图的连通子图。而无向图的一个极大连通子图（不存在包含它的更大的连通子图）则称为该图的【连通分量】。
连通子图：无向图的子图是连通无向图，则该子图为原图的连通子图；
极大连通子图：无向图中一个连通子图，且不存在包含它的更大的连通子图；
连通分量：无向图中的一个极大连通子图。
上图中右侧的非连通无向图，其本身是非连通的，但 v1, v2, v3, v4 与其相连的边构成的子图是连通的，且不存在包含它的更大的连通子图了，所以该图是原图的一个连通分量。注意，顶点 v5, v6 与其相连的边构成的子图也符合定义，也是原图的一个连通分量。
强连通图和强连通分量
有向图中，如果顶点 vi 到 vj 有路径，并且从顶点 vj 到 vi 也有路径，则称两顶点是连通的。
强连通有向图：图中任意两个顶点都有路径；
非强连通有向图：存在某顶点无法到达其他任何顶点；
有向图的一个极大强连通子图称为该图的 强连通分量。
上图中，右侧 v1, v2, v3, v4, v5, v6 与其相连的边构成的子图是原图的一个强连通分量，注意顶点 v7 构成的子图，也是原图的一个强连通分量。
带权图
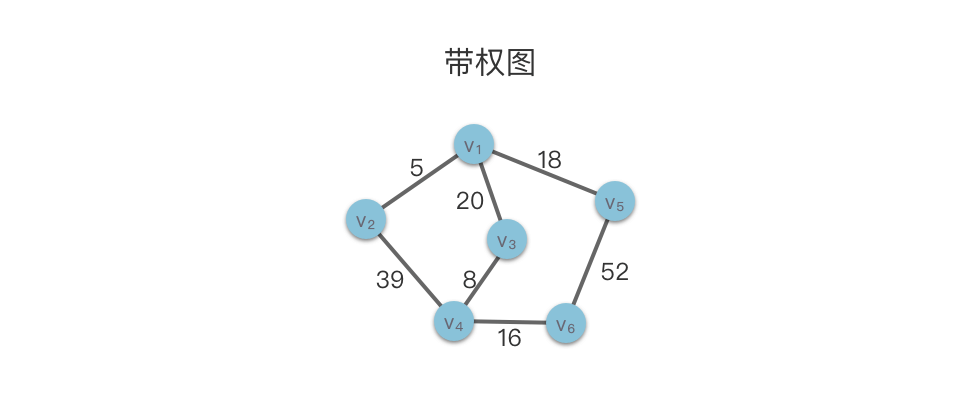
图不仅需要表示顶点之间是否存在某种关系，还需要表示这一关系的具体细节。则需要在边上带一些数据信息，这些信息称为 权 。在具体应用中，权值可以具有某种具体意义，如权值可以代表距离、时间及价格等不同属性。
带权图：图的每条边都被赋予一个权值；
网络：带权的连通无向图。
二，图的存储结构
图的结构比较复杂，需要表示顶点和边。一个图可能有任意多个顶点，任何两个顶点之间都可能存在边。在实现图的存储时，重点关注边与顶点之间的关联关系，这是图存储的关键。
图的存储可以通过【顺序存储结构】和【链式存储结构】来实现。其中顺序存储结构包括邻接矩阵和边集数组；链式存储结构包括邻接表，链式前向量等。
1. 邻接矩阵（Adjacency Matrix）
使用一个二维数组 adjmatrix 来存储顶点之间的邻接关系。
无权图：adjmatrix[i][j] = 1表示顶点 vi 到 vj 存在边。adjmatrix[i][j] = 0 表示顶点 vi 到 vj 不存在边；
带权图：adjmatrix[i][j] = w 且 w != float('inf') ，表示顶点 vi 到 vj 的权值为 w，adjmatrix[i][j] = float('inf') 表示顶点 vi 到 vj 不存在边。
特点：
优点：实现简单，且可以直接查询顶点 vi 与 vj 之间是否有边存在，可以直接查询边的权值；
缺点：初始化效率和遍历效率低，空间利用率低，且不能存储重复边，也不便于增删节点。
class adjMatrix:
def __init__(self, ver_count):
self.ver_count = ver_count
self.adj_matrix = [[None for _ in range(ver_count)] for _ in range(ver_count)]
def __valid(self, v):
return 0 <= v <= self.ver_count
def creatGraph(self, edges = []):
for vi, vj, val in edges:
self.add_edge(vi, vj, val)
def add_edge(self, vi, vj, val):
if not self.__valid(vi) or not self.__valid(vj):
raise ValueError(str(vi) + 'or' + str(vj) + 'is not i valid vertex.')
self.adj_matrix[vi][vj] = val
def get_edge(self, vi, vj):
if not self.__valid(vi) or not self.__valid(vj):
raise ValueError(str(vi) + 'or' + str(vj) + 'is not i valid vertex.')
return self.adj_matrix[vi][vj]
def printGraph(self):
for vi in range(self.ver_count):
for vj in range(self.ver_count):
val = self.get_edge(vi, vj)
if val:
print(str(vi) + ' - ' + str(vj) + ' : ' + str(val))
时间复杂度：
初始化 O(n ^ 2)
查询，添加或删除 O(1)
获取某个节点所有边 O(n)
图的遍历 O(n ^ 2)
空间复杂度 O(n ^ 2)
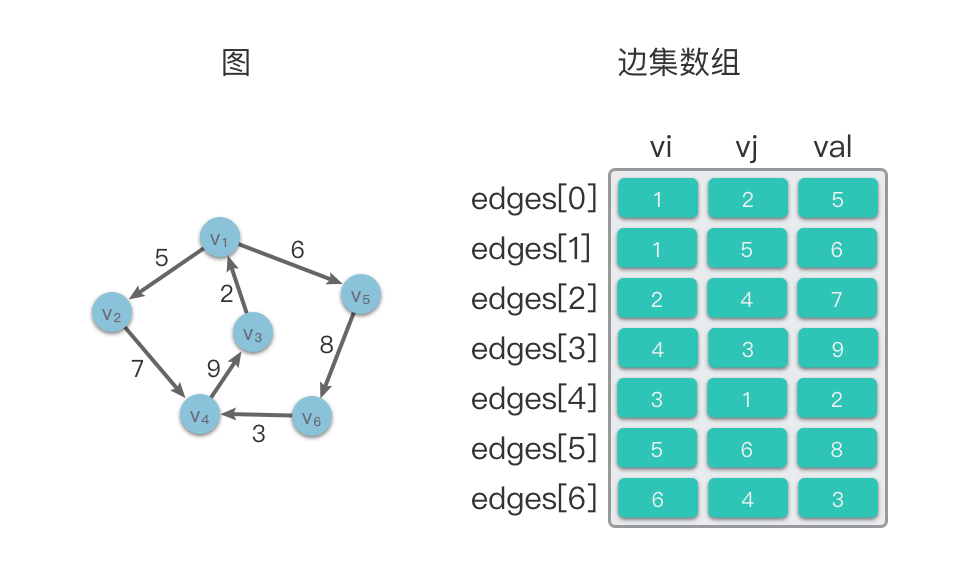
2. 边集数组（Edgeset Array）
使用一个数组来存储顶点之间的邻接关系。数组中的每个元素都包含一条边的起点vi，终点vj和边的权值 val。
class EdgeNode:
def __init__(self, vi, vj, val):
self.vi = vi
self.vj = vj
self.val = val
class EdgesetGraph:
def __init__(self):
self.edges = []
def creatGraph(self, edges = []):
for vi, vj, val in edges:
self.add_edge(vi, vj, val)
def add_edge(self, vi, vj, val):
edge = EdgeNode(vi, vj, val)
self.edges.append(edge)
def get_edge(self, vi, vj):
for edge in self.edges:
if vi == edge.vi and vj == edge.vj:
val = edge.val
return None
def printGraph(self):
for edge in self.edges:
print(str(edge.vi) + ' - ' + str(edge.vj) + ' : ' + str(edge.val))
3. 邻接表（Adjacency List）
使用顺序存储和链式存储相结合的存储结构在存储图的顶点和边。其数据结构其一是数组，主要用来存放顶点的数据信息，其二是链表，用来存放边信息。
在邻接表的存储方法中，对于图中的每个节点建立一个线性链表，把所有邻接于 vi 的顶点链接到单链表上。
在每个顶点的前面设置一个表头节点，称之为【顶点节点】。每个顶点节点由【顶点域】和【指针域】组成。其中顶点域用于存放某个顶点的数据信息，指针域用于指出该顶点的第 1 条边对应的链节点。
为了方便随机访问任意顶点的链表，使用一组顺序存储的数组存储所有【顶点节点】部分，数组的下标表示顶点在图中的位置。
class AdjListNode:
def __init__(self, vj, val):
self.vj = vj
self.val = val
self.next = None
class VertexNode:
def __init__(self, vi):
self.vi = vi
self.head = None
class AdjList:
def __init__(self, ver_count):
self.ver_count = ver_count
self.vertices = []
for vi in range(ver_count):
vertex = VertexNode(vi)
self.vertices.append(vertex)
def __valid(self, v):
return 0 <= v <= self.ver_count
def creatGraph(self, edges = []):
for vi, vj, val in edges:
self.add_edge(vi, vj, val)
def add_edge(self, vi, vj, val):
if not self.__valid(vi) or not self.__valid(vj):
raise ValueError('It is not a valid vertex')
vertex = self.vertices[vi]
edge = AdjListNode(vj, val)
edge.next = vertex.head
vertex.head = edge
def get_edge(self, vi, vj):
if not self.__valid(vi) or not self.__valid(vj):
raise ValueError('It is not a valid vertex')
vertex = self.vertices[vi]
cur_edge = vertex.head
while cur_edge:
if cur_edge.vj == vj:
return cur_edge.val
cur_edge = cur_edge.next
return None
def printGraph(self):
for vertex in self.vertices:
cur_edge = vertex.head
while cur_edge:
print(str(vertex.vi) + ' - ' + str(cur_edge.vj) + ' : ' + str(cur_edge.val))
cur_edge = cur_edge.next
时间复杂度：
初始化和创建 O(m + n)
查询存在 vi 到 vj 的边 O(TD(vi))
遍历某个点的所有边 O(TD(vi))
遍历整张图 O(m + n)
空间复杂度 O(m + n)
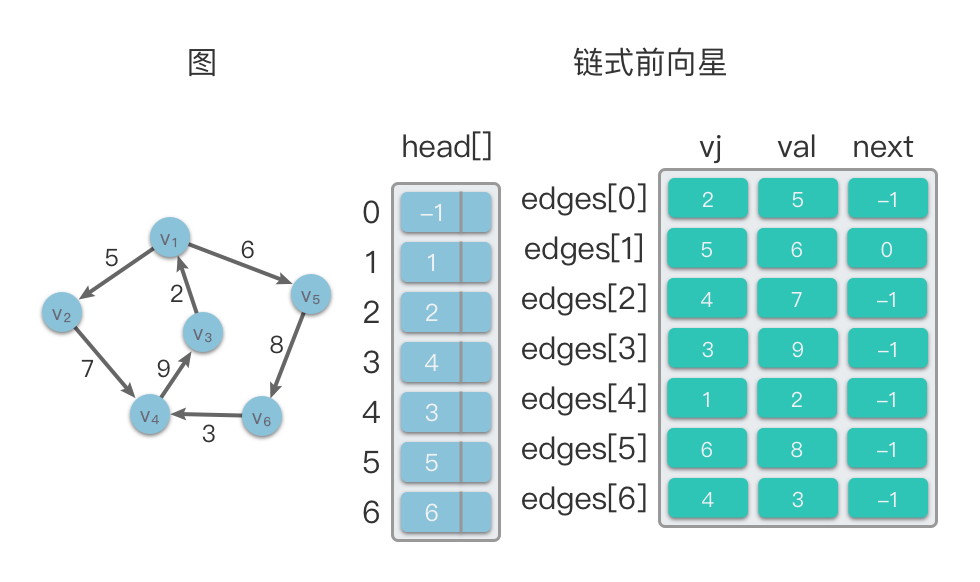
4. 链式前向星（Linked Forward Star）
实质上是使用静态链表实现的邻接表，也叫做静态邻接表，将边集数组和邻接表相结合，可以快速访问一个节点所有的邻接点，并且使用很少的额外空间。
特殊的边集数组 edges：其中 edges[ i ] 表示第 i 条边，edges[i].vj 表示第 i 条边的终止点，edges[i].val 表示第 i 条边的权值，edges[i].next 表示与第 i 条边同起始点的下一条边的存储位置。
头节点数组 head：其中 head[ i ] 存储以顶点 i 为起始点的第 1 条边在数组 edges 中的下标。
class forwardStarNode:
def __init__(self, vj, val):
self.vj = vj
self.val = val
self.next = None
class forwardStar:
def __init__(self, ver_count, edge_count):
self.ver_count = ver_count
self.edge_count = edge_count
self.head = [-1 for _ in range(ver_count)]
self.edges = []
def __valid(self, v):
return 0 <= v <= self.ver_count
def creatGraph(self, edges = []):
for i in range(len(edges)):
vi, vj, val = edges[i]
self.add_edge(i, vi, vj, val)
def add_edge(self, index, vi, vj, val):
if not self.__valid(vi) or not self.__valid(vj):
raise ValueError('It is not a valid vertex.')
edge = forwardStarNode(vj, val)
edge.next = self.head[vi]
self.edges.append(edge)
self.head[vi] = index
def get_edge(self, vi, vj):
if not self.__valid(vi) or not self.__valid(vj):
raise ValueError('It is not a valid vertex.')
index = self.head[vi]
while index != -1:
if vj == self.edges[index].vj:
return self.edges[index].val
index = self.edges[index].next
return None
def printGraph(self):
for vi in range(self.ver_count):
index = self.head[vi]
while index != -1:
print(str(vi) + ' - ' + str(self.edges[index].vj) + ' : ' + str(self.edges[index].val))
index = self.edges[index].next时间复杂度：
初始化和创建 O(m + n)
查询存在 vi 到 vj 的边 O(TD(vi))
遍历某个点的所有边 O(TD(vi))
遍历整张图 O(m + n)
空间复杂度 O(m + n)
5. 哈希表实现邻接表
在Python中，可以通过字典（哈希表）实现邻接表：
第一个字典主要用来存放顶点的数据信息，字典的键是顶点，值是该点所有邻边构成的
另一个字典；
另一个字典是用来存放顶点相连的边信息，地点的键是边的终点，值是边的权重。
class HashNode:
def __init__(self, vi):
self.vi = vi
self.adj_edges = dict()
class HashGraph:
def __init__(self):
self.vertices = dict()
def creatGraph(self, edges = []):
for vi, vj, val in edges:
self.add_edge(vi, vj, val)
def add_vertex(self, vi):
vertex = HashNode(vi)
self.vertices[vi] = vertex
def add_edge(self, vi, vj, val):
if vi not in self.vertices:
self.add_vertex(vi)
if vj not in self.vertices:
self.add_vertex(vj)
self.vertices[vi].adj_edges[vj] = val
def get_edge(self, vi, vj):
if vi in self.vertices and vj in self.vertices[vi].adj_edges:
return self.vertices[vi].adj_edges[vj]
return None
def printGraph(self):
for vi in self.vertices:
for vj in self.vertices[vi].adj_edges:
print(str(vi) + ' - ' + str(vj) + ' : ' + str(self.vertices[vi].adj_edges[vj]))
时间复杂度：
初始化和创建 O(m + n)
查询存在 vi 到 vj 的边 O(1)
遍历某个点的所有边 O(TD(vi))
遍历整张图 O(m + n)
空间复杂度 O(m + n)
算法通关手册（LeetCode） | 算法通关手册（LeetCode）
原文内容在这里，如有侵权，请联系我删除。
916
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
