计算机的运算方法--乘法运算

文章目录

• 前言
• 一、乘法运算的分类
• 二、乘法运算简介
  • 1.原码一位乘法
  • 2.原码两位乘法
  • 3.补码一位乘法
  • 4.补码两位乘法

---

前言

在计算机中，乘法运算是一种很重要的的运算，有的机器直接由硬件乘法器完成乘法运算，有的机器内没有乘法器，但可以按机器做乘法运算的方法，用软件编程实现。因此，学习乘法运算有助于乘法器的设计，也有助于乘法编程。

一、乘法运算的分类

简单来说乘法运算基础主要分为四类：1.原码一位乘法，2.原码二位乘法，3.补码一位乘法，4.补码二位乘法。

二、乘法运算简介

1.计算机乘法方式由来

 计算机的乘法运算是根据乘法笔算的方式改进得到。

          乘法笔算方式特点：1.被乘数A左移多次。

                                           2.4个积位的相加运算。

           但是不难发现笔算乘法的方式不适合计算机的运算方式;

                                           1.4个积位难以一次相加。

                                            2.乘积位数增加一倍，造成器材浪费，时间增加。

            改进方式：

              由此可得：两数相乘的过程可以看为加法和移位的过程两种运算（2^-1可以看做向右移位），这对计算机来说是非常容易实现的。

              假定被乘数A = 0.1101， 乘数B = 0.1011。 我们根据上面的分析可以得到下面的步骤过程。

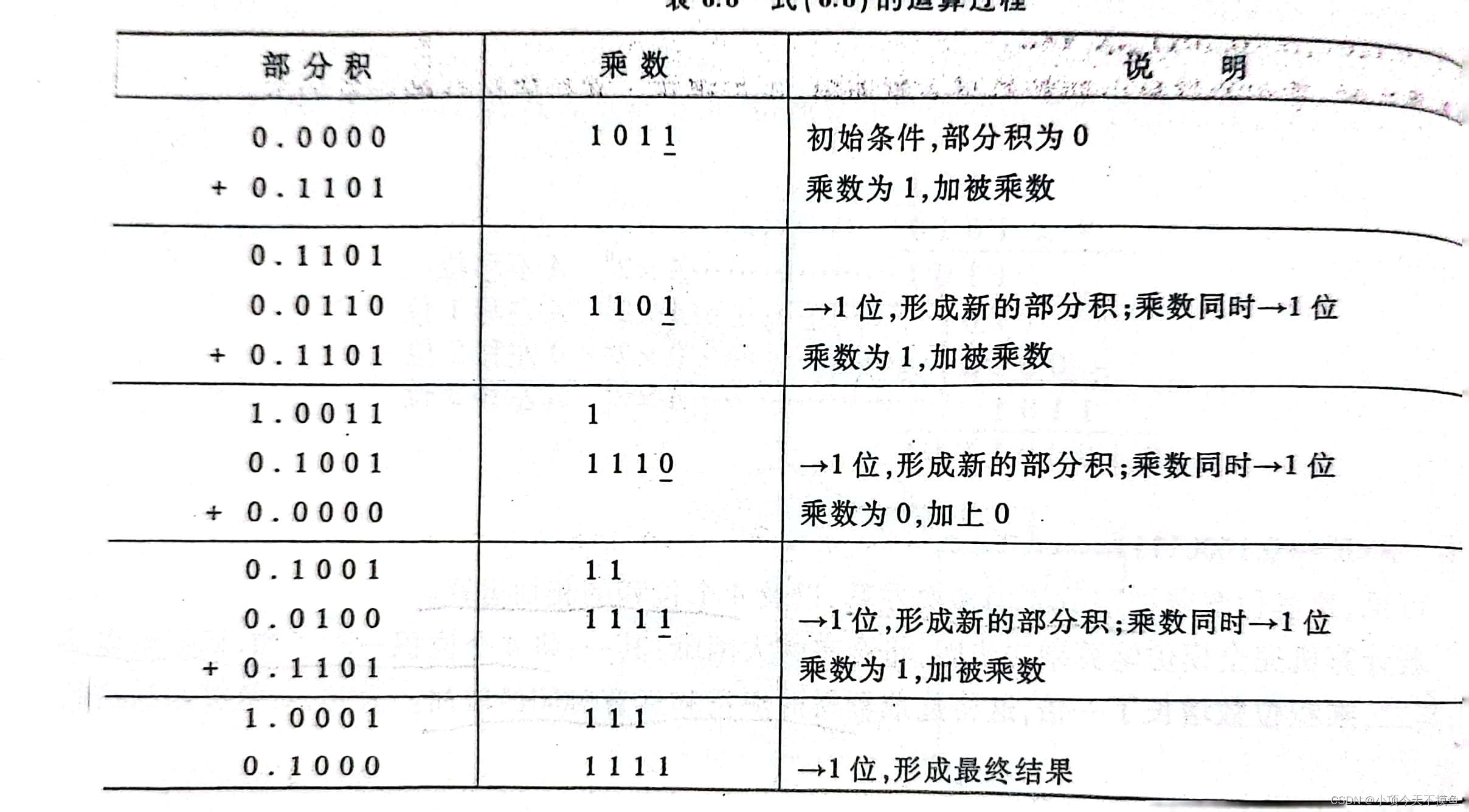
有上述运算过程可以归纳如下：

       1.两个n位数相乘需要经过n次加法运算，n次移位。

       2.由乘数的末尾来确定被乘数是否与 原部分积相加，然后右移一位，形成行的部分积，同时乘数也右移一位，由次低位作为新的末尾，空出的最高位放部分积的最低位。

      3.每次做加法，部分积的最高位和被乘数相加。

2、原码一位乘法

原码乘法的过程和上述数值相乘的过程基本相似，但是有几个注意点：

       1：乘积的符号由乘数和被乘数的符号异或得到。

       2：乘积的数值由乘数和被乘数的数值绝对值相乘得到。

       3：部分积取 n + 1 为来确保过程中绝对值 >= 1 的情况。

       4：过程中的部分积的移位全都为逻辑移位。（因为是两个实数相乘没有符号）。

3、原码两位数相乘

为了提高运算速率可以采用原码两位乘法，和原码一位乘法类似，符号位和数值位分开运算，采用两位乘数来决定部分积来提高效率。

        我们不难知道两位乘数可以得到四种状态，分别对应了四种操作，如下：

        其中的2倍被乘数的操作可以通过左移移位得到。但是三倍被乘数的操作比较难以得到，我们可以把3 = 4 - 1（11 = 100 - 1）；可以先完成减去一倍被乘数的操作，第二步完成加上四倍被乘数的操作。 这样的话我们可以在完成的第一步以后，将“加上四倍被乘数的操作”来记录在Cj触发器中（看作进位），左移两位部分积，高两位乘数+1来完成第二步。

         两位乘数结合Cj寄存器共有三位，共有八种情况，如下：

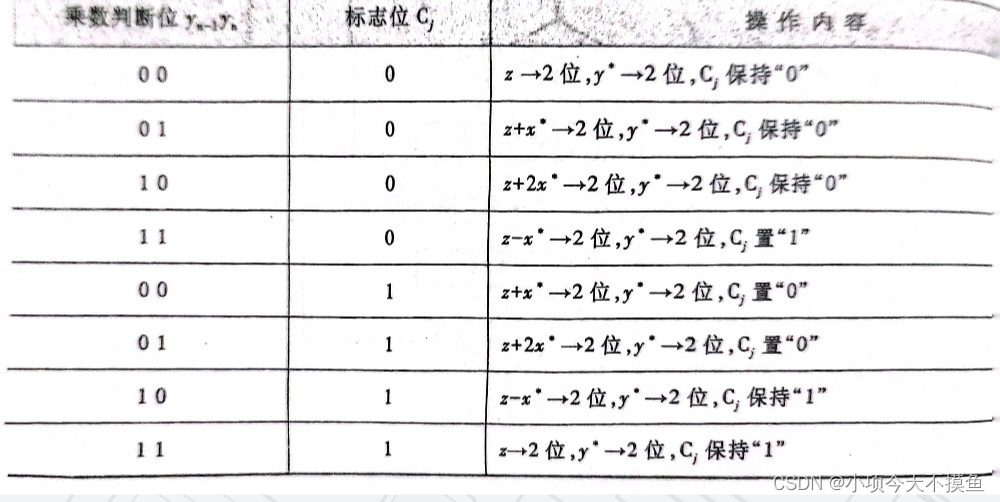
        在进行-x*运算的时候，计算机一般都采用+【-x】补来实现，所以在计算过程中参与运算的是操作数绝对值的补码，运算过程的右移操作要遵循补码的移位规则。还有过程中出现的+【2x】补使部分积的绝对值>2,所以采用三位符号位来确保无误，其中最高位为真正的符号位。 

       此外与原码一位乘法不同的是，如果乘数的位数为偶数那么需要在最高位补00，奇数则补0。这是因为为了避免Cj寄存器存在1的情况未参加运算。所以最后一次运算不需要进行移位。

       不难分析，位数为偶数需要做n / 2 + 1 次加法， n / 2 次 移位。

                                    奇数时做n  / 2 + 1 次加法，移位。

原码的乘法实现比较容易，但是由于机器都采用补码做加减运算，若做乘法前将补码转换成原码，相乘之后又将负积的原码转换成补码形式增添了许多操作步骤，反而是运算变得复杂。为此有不少机器直接用补码相乘，机器里配置实现补码相乘的乘法器，避免了码制转换，提高了机器效率。

3、补码一位乘法

         补码一位乘法基础分为两种，一种是分开根据乘数的符号区别操作（也叫校验法），第二种是被乘数和乘数的符号均为任意（也叫Booth算法，可以由校验法导出）。

         校验法：

         1.乘数的符号位为正，就可以按照原码的运算规则来进行运算，但是移位和加和要按照补码规则运算。

          2.乘数的符号位为负，前面和乘数为正数的情况一样，只需要在最后一项加上[-x]补即可。

注意点：考虑到运算时可能出现绝对值 >= 1的情况（此刻没有溢出），所以部分积和被乘数取双符号位。

          booth算法：

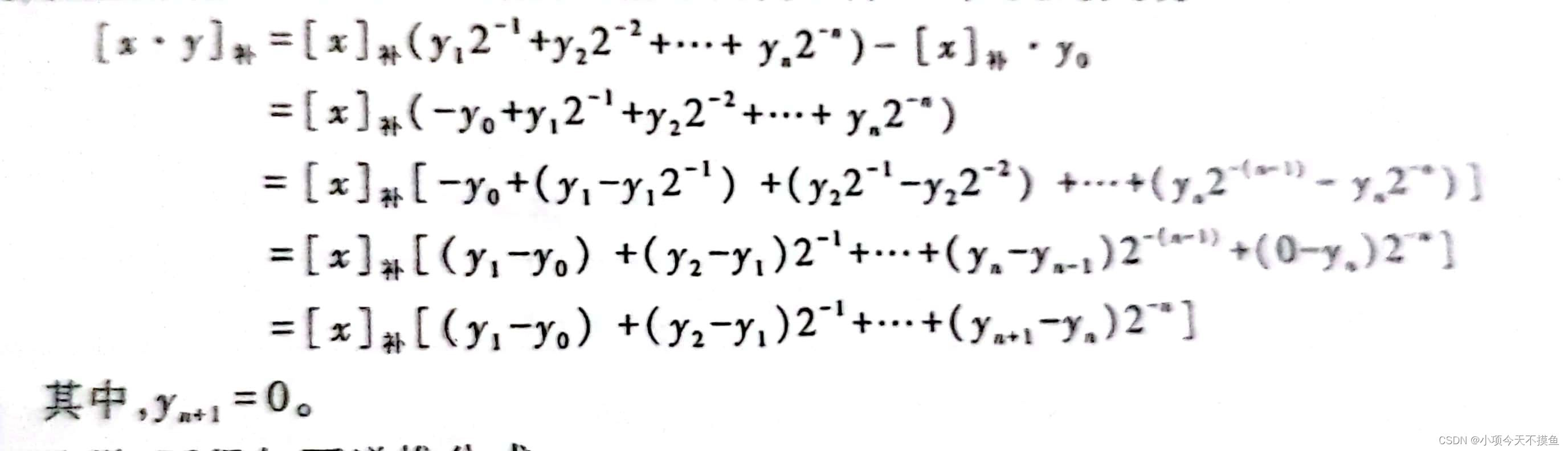
 可以发现，开始时yn+1 = 0，部分积 = 0；每一步由（yi+1 - yi）确定部分积加上[x]补或[-x]补或0。由此重复n步，直到y1 - y0，但是这一步不移位。

        这里yi+1yi一共有四种情况对应相应的操作：

 

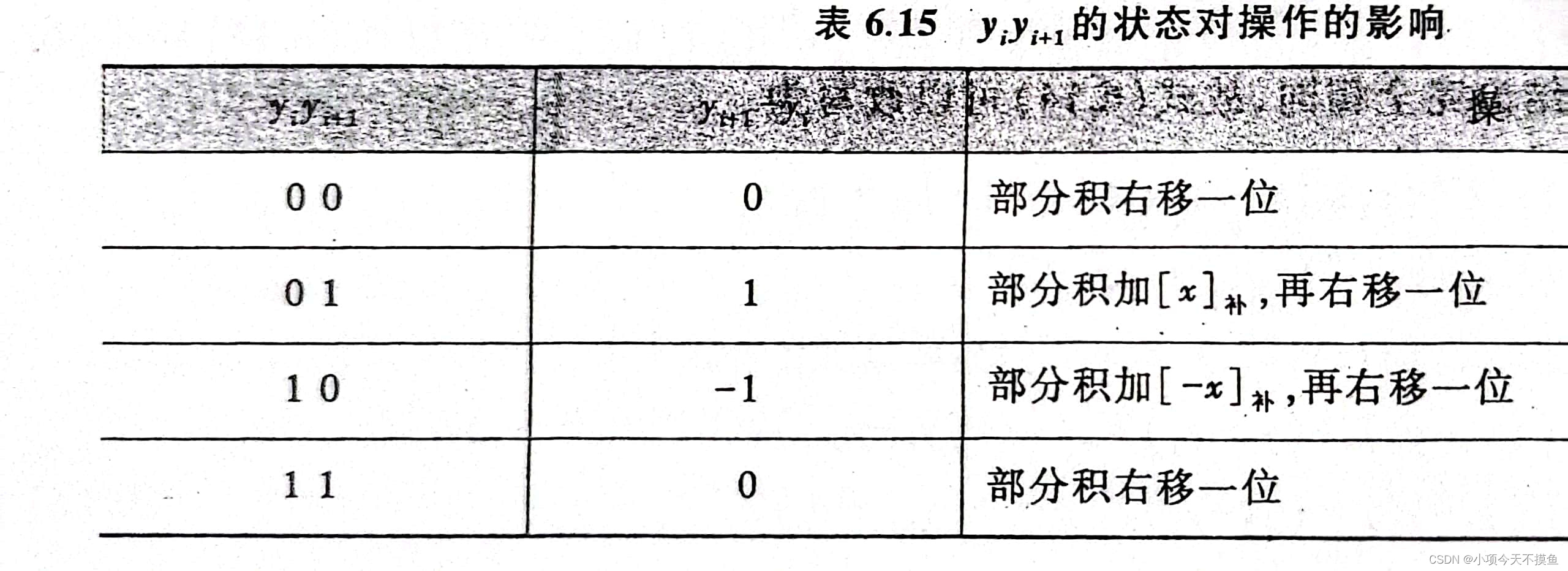
 值得注意的是补码的乘法也要像加减法一样符号位参与运算。

 这里部分积和被乘数的符号位和校验法一样取双符号位，但是由于乘数的符号位参与运算，所以乘数多一位。

4、补码两位乘法

        补码两位乘法运算规则的本质就是根据补码一位乘法的运算规则结合yn-1ynyn+1三位的状态合并成一次操作；

        不难发现yn-1ynyn+1一共有三位对应八种状态，操作如下：

 操作中出现加2【x】补加2【-x】补，左移被乘数的操作，都可能因为溢出侵占两位符号位，所以取三位符号位。如果乘数y的尾数位数为奇数，则采用单符号位，并且运算的最后一步移一位；如果乘数y尾数的位数为偶数，则采用双符号位，并且运算的最后一步要不移位。