动态规划-拔萝卜问题

问题：小白兔从一片田地的左上角进入，右下角离开，田地中每个方格里有数量不等的萝卜供小白兔拿取，小白兔必须尽快离开田地以降低被猎人发现的概率(即小白兔每次必须选择向下或者向右走一格，并拿走格子里的萝卜)，在保证尽可能安全的前提下，尽可能获得最多萝卜，请为小白兔规划一条最佳的拿萝卜路径。

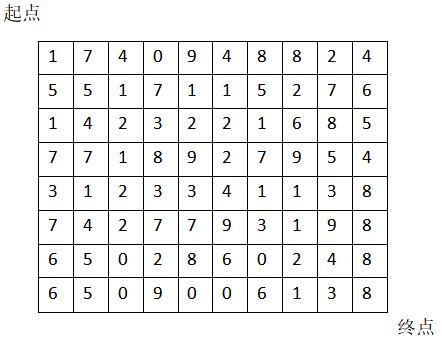
采用动态规划法，即从左上角开始，将紧邻的上方和左方的数进行比较，取其中加大的数与本格代表的数相加作为萝卜总数写入对应的萝卜矩阵，如果上方或左方没有数则不参与运算。依次类推可以在在萝卜矩阵的右下方得到本体的最优解。

如图：

代码如下：

#include<stdlib.h>
#include<stdio.h>
#include <time.h>
const int M=8;//萝卜地行数
const int N=10;//萝卜地列数
int v[M][N],c[M][N];//萝卜数矩阵，最优萝卜数矩阵 
int dituiluobo(int m,int n)
{
    //分四种情况计算最优萝卜矩阵 
    for(int i=0;i<=m;i++)
        for(int j=0;j<=n;j++)
        {
            if(i==0&&j==0) c[0][0]=v[0][0];//入口即出口 
            if(i==0&&j!=0) c[i][j]=c[i][j-1]+v[i][j];//最上面一行 
            if(i!=0&&j==0) c[i][j]=c[i-1][j]+v[i][j];//最左侧一列 
            if(i!=0&&j!=0){ //其他部分 
                if(c[i-1][j]>=c[i][j-1]){
                    c[i][j]=v[i][j]+c[i-1][j];
                }else if(c[i][j-1]>c[i-1][j]){
                    c[i][j]=v[i][j]+c[i][j-1];
                }
            }
        }
    return 0;//返回最优萝卜矩阵右下角的值 
}

int main()
{
    int i,j,count;
    printf("一片萝卜地如下：\n");
    for(i=0;i<M;i++)
    {
        for(j=0;j<N;j++)
        {
            v[i][j]=rand()%10;
            c[i][j]=0;
            printf("%d  ",v[i][j]);
        }
        printf("\n");
    }
    count=dituiluobo(M-1,N-1);
    printf("递推小萝卜最优结果为%d\n",c[M-1][N-1]);
    printf("最优萝卜矩阵如下：\n");
    for(i=0;i<M;i++)
    {
        for(j=0;j<N;j++)
        {
            //printf("%d  ",c[i][j]);
            if(c[i][j]>=10){
                printf("%d  ",c[i][j]);
            }else if(c[i][j]<10){
                printf("%d   ",c[i][j]);
            }
        }
        printf("\n");
    }
    
    return 0;
}