【一起撸个深度学习框架】6 折与曲的相会——激活函数

清风莫追

已于 2023-08-15 11:53:11 修改

阅读量783

点赞数 48

分类专栏： # 一起撸个DL框架文章标签：深度学习 python 人工智能算法

于 2023-05-15 20:57:26 首次发布

本文链接：https://blog.csdn.net/m0_63238256/article/details/130691899

版权

一起撸个DL框架专栏收录该内容

6 篇文章 7 订阅

订阅专栏

CSDN个人主页：清风莫追
欢迎关注本专栏：《一起撸个DL框架》
GitHub获取源码：https://github.com/flying-forever/OurDL
blibli视频合集：https://space.bilibili.com/3493285974772098/channel/series

文章目录

6 折与曲的相会——激活函数🍈

6 折与曲的相会——激活函数🍈

1 前言

在上一节，我们实现了一个“自适应线性单元”，不断地将一个一次函数的输入和输出“喂”给它，它就可以自动地找到一次函数 $y = w x + b$ 中合适的参数值w和b。计算图通过前向传播和反向传播，初步展现了它的神奇之处。

但在实际遇到的问题中，输入与输出之间往往并不是简单的线性关系，它们之间的函数关系可能是二次的、指数、甚至分段的。此时”自适应线性单元“就不足以满足我们的需求了。而”激活函数“，将为计算图带来一种拟合这些非线性函数关系的能力。

同时为了得到对于激活函数更加清晰和形象化的认知，本节我们还将使用matplotlib对拟合过程进行一些可视化的展现。

本节任务：在计算图中加入激活函数relu，拟合二次函数 $y=x^2$ 在区间[0,2]的一小段曲线。

可视化效果：


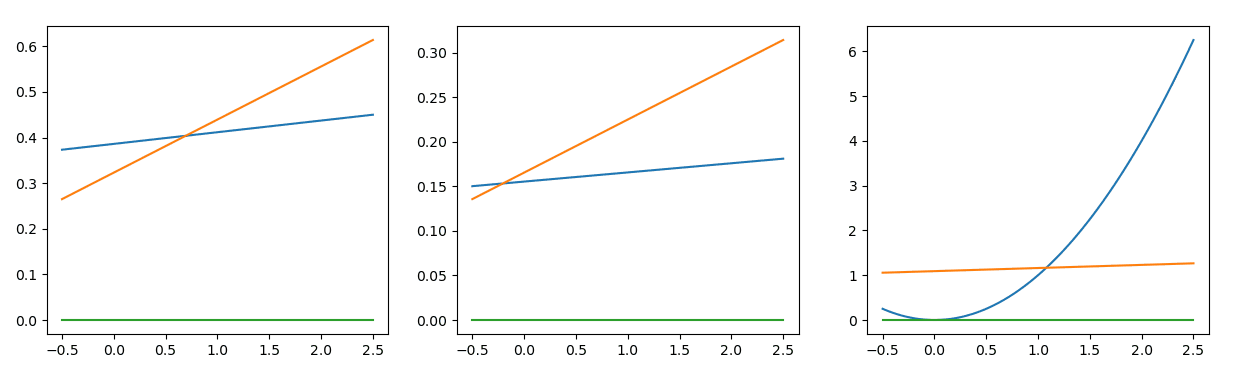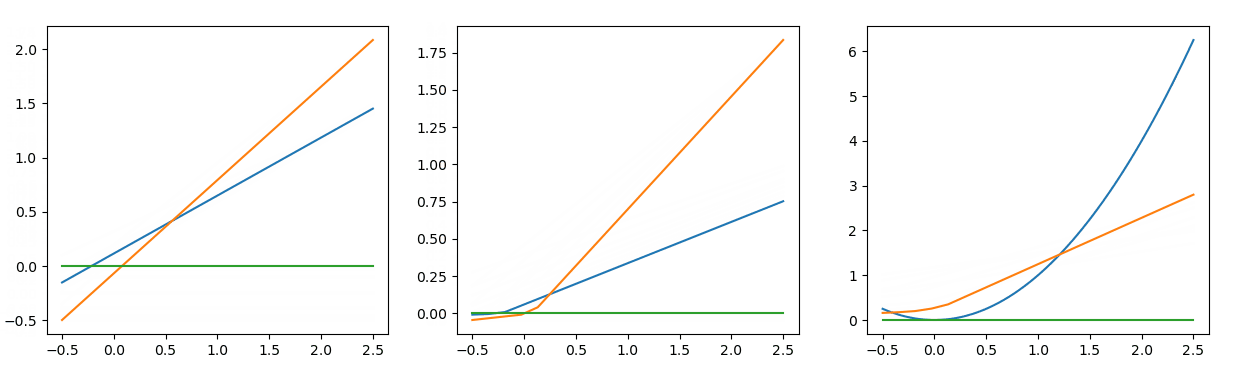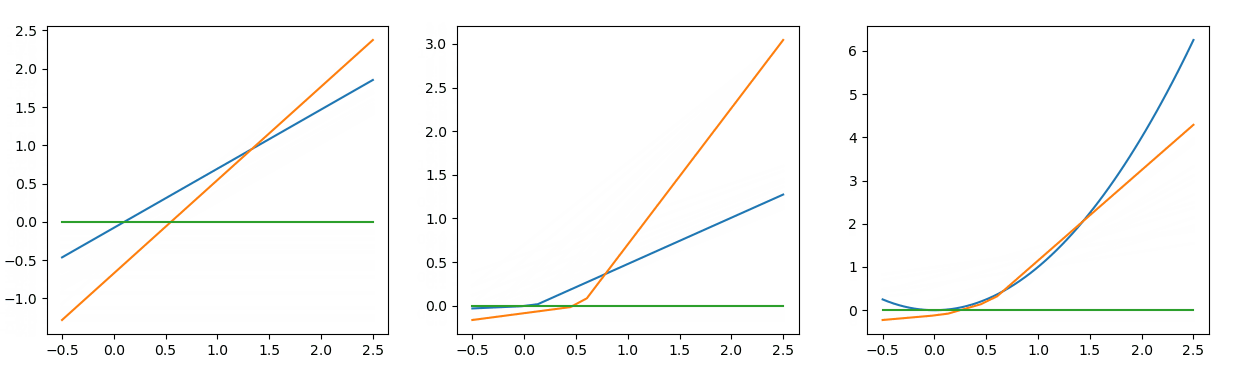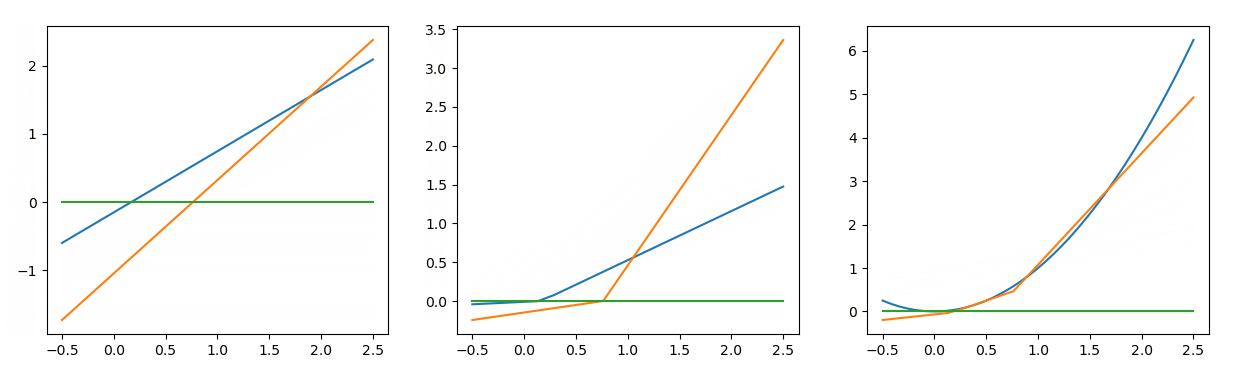图1：二次函数拟合动画

2 激活函数

关于”激活函数“这个名称（非专业解释），首先我们可以看阶跃函数。当输入超过0这个阈值时，输出就从0跳到了1，0是一个非激活的状态，而1是一个激活的状态。这个和生物领域中神经元间的突触有一定相似性，当突触间的兴奋性神经元递质超过某个阈值后，下一个神经元才会进入兴奋状态继续传递信号。
$f(x)=\begin{cases} 0, & x<0 \\ 1, & x>=0 \end{cases}$


图2：阶跃函数的图像

2.1 Relu

人们发明了许多各式各样的激活函数，它们有着不同的特点，而Relu是其中比较常用的一种。Relu是一个简单的分段函数，它的核心思想是通过多段折线来贴近曲线，折线段越多、越短，拟合效果就越好，理论上使用relu几乎可以较好地任何曲线。
$relu(x)=\begin{cases} x, & x>=0 \\ 0, & x<0 \end{cases}$


图3：Relu函数图像

Relu节点的实现：

# ourdl/ops/ops.py
class Relu(Op):
    def compute(self):
        assert len(self.parents) == 1
        self.value = self.parents[0].value if self.parents[0].value >= 0 else 0
    def get_parent_grad(self, parent):
        return 1. if self.parents[0].value > 0 else 0  # 发现relu的导函数就是step
    @staticmethod
    def relu(x: float):
        '''静态方法 --> 在计算图之外使用relu'''
        return x if x >= 0. else 0.

在前向传播的过程中，它接受一个父节点的输入，并产生一个输出。我们还使用装饰器@staticmethod，实现了一个静态方法relu(x)，这样我们也可以在计算图之外直接调用relu函数了，例如可以在使用matplotlib绘制函数图像时用到。

2.3 LeakyRelu

和加法节点、乘法节点等节点一样，激活函数也是计算图中的一个运算节点，需要在该节点类中实现对应的get_parent_grad()方法对父节点进行求导。Relu函数在输入小于0时函数值都是0，对应的导数也是0，这种情况下参数就不会进行更新了。

人们提出了一种对Relu函数的修正方案，那就是LeakyRelu。在输入大于等于0的部分函数值不变，仍然是x；但是在输入小于0的部分取 $0.1 x$ ，这样在反向传播的过程中，节点的输入小于0时，虽然导数只有0.1，但并没有直接消失，参数仍然可以进行更新。（这里0.1是一个”超参数“，也可以取其它值）

在我的一些尝试中，使用Relu函数时训练过程会卡住一直无法拟合，但LeakyRelu可以一定程度上缓解问题，仍然可以拟合只是比较慢。


图4：LeakyRelu的函数图像

LeakyRelu节点的实现：

# ourdl/ops/ops.py
class LeakyRelu(Op):
    '''消除了relu中导数为0的情况'''
    def compute(self):
        assert len(self.parents) == 1
        t = self.parents[0].value
        self.value = t if t >= 0 else t * 0.1
    def get_parent_grad(self, parent):
        return 1. if self.parents[0].value > 0 else 0.1  # 发现relu的导函数就是step
    @staticmethod
    def relu(x: float):
        '''静态方法 --> 在计算图之外使用leakyrelu'''
        return x if x >= 0. else x * 0.1

超参数”0.1"直接写死在代码中了，因为它通常并不需要改变。

3 拟合曲线的尝试

3.1 设计计算图


图5：计算图的设计

这个计算图中明确地画出了所有的节点，看起来有一些复杂。从整体看，计算图包含了三次变换：

$输入 - - > 线性变换 - - > 激活函数 - - > 线性变换 - - > 输出$

上述三次变换各自的意义是什么？计算图为什么设计成这个样子？这都是很重要的问题。

其实在图一中大致就能得到答案。

第一次变换，产生两条不同的直线，它们有着不同的斜率，更重要的是：它们与x轴有着不同的交点。
第二次变换，使用激活函数relu（图一中是LeakyRelu)，两条直线都在与x轴的交点处折断，得到两条折线。
第三次变换，两条折线线性叠加，由于它们折断点不同，故得到是一个三段折线。

而我所希望的，就是利用三段的折线去尽可能地贴合二次函数的曲线。

3.2 实现训练过程

1、计算图的搭建：

# example/01_esay/04_relu与二次拟合.py
import sys
sys.path.append('../..')  # 父目录的父目录
from ourdl.core import Varrible
from ourdl.ops import Mul, Add
from ourdl.ops.loss import ValueLoss
from ourdl.ops import LeakyRelu as Relu
import matplotlib.pyplot as plt
import numpy as np
import random

# 1.1 线性变换一
x = Varrible()
w_11 = Varrible()
w_12 = Varrible()
mul_11 = Mul([x, w_11])
mul_12 = Mul([x, w_12])
b_11 = Varrible()
b_12 = Varrible()
add_11 = Add([mul_11, b_11])
add_12 = Add([mul_12, b_12])
# 1.2 激活函数 --> 非线性变换
relu_11 = Relu([add_11])
relu_12 = Relu([add_12])
# 1.3 线性变换二
w_21 = Varrible()
w_22 = Varrible()
mul_21 = Mul([relu_11, w_21])
mul_22 = Mul([relu_12, w_22])
b_21 = Varrible()
add_21 = Add([mul_21, mul_22, b_21])
# 1.4 损失函数
label = Varrible()
loss = ValueLoss([label, add_21])

在完成计算图的设计后，搭建的过程比较简单，就是一些节点的创建和连接。由于节点的数量比较多，因此稍有些繁琐，后面我们会实现一些对象和方法用于批量创建和连接节点以及计算图的封装，简化计算图的搭建过程。一个个节点地创建也有其优势——灵活。

2、初始化计算图参数

# example/01_esay/04_relu与二次拟合.py
# 2 参数初始化
params = [w_11, w_12, b_11, b_12, w_21, w_22, b_21]
for param in params:
    param.set_value(random.uniform(-1, 1))
print([param.value for param in params])

这里调用了random库，使用均匀分布进行参数的随机初始化。将所有需要训练的参数加入到了一个列表params中，方便批量进行初始化以及后面的参数更新。

有时为了对比多次训练的效果，需要进行固定的初始化（初始化有时可以很大程度地影响训练效果），你可以手动地指定这些参数的初始值，例如

values = [-0.1571950013426796, -0.1070365984042347, 0.3791639008324807, 0.31960284774415215, 0.4263410176300597, 0.5097967360623379, 0.7597168751185974]
for i in range(len(params)):
    params[i].set_value(values[i])

如果你使用的是Relu激活函数而不是LeakyRelu，同时采用随机参数初始化，你将发现你的训练时而成功时而失败。

3、构造训练数据

# example/01_esay/04_relu与二次拟合.py
# 3 生成数据
data_x = [random.uniform(0, 2) for i in range(1500)]  # 似乎实数比离散的[0, 1, 2]要好
data_label = [x * x for x in data_x]

使用均匀分布，在[0, 2]的范围内生成了1500个随机值，作为输入的x。然后使用了列表推导式得到对应的二次函数输出值，作为计算图中的标签。

4、训练过程

# example/01_esay/04_relu与二次拟合.py
# 4 开始训练
losses = []
for i in range(len(data_x)):
    x.set_value(data_x[i])
    label.set_value(data_label[i])
    loss.forward()
    for param in params:
        param.get_grad()
        param.update(lr=0.01)
    if i % 100 == 0:
        print(f'[{i}]:loss={loss.value},', [param.value for param in params])
    losses.append(loss.value)
    loss.clear()

# 5 画出训练过程中loss的变化曲线
show_x = [i for i in range(len(losses))]
show_y = [_ for _ in losses]
plt.plot(show_x, show_y)
plt.show()

训练过程与上一节“自适应线性单元”基本相同。在第三步构造训练数据时，我们生成了1500个数据样本，因此绘制曲线来观察训练过程中的损失变化会更加直观。我们使用losses列表记录了每次参数更新后的损失值，并使用matplotlib库绘制损失的变化曲线。

3.3 训练效果

这里我们就完成了训练过程的所有代码编写，让我们运行一下代码看看效果吧！


图6：损失变化曲线

可以看到随着训练过程的进行，损失值呈下降的趋势，并渐渐趋于平稳。损失值越低表示着模型的输出越准确，我们的模型看起来好像训练得还不错。

但只看损失函数其实还是不太直观，我们可以直接将模型所表示的函数，与二次函数 $y=x^2$ 画在一起，看看它们到底贴得近不近。

3.4 训练过程的可视化动画

当然，我觉得只看一个最后的贴合结果还不够，甚至只看输出的结果也仍然不能很清晰地了解训练的过程。所以我决定将中间节点的输出也画出来，并随着训练的过程以动画的形式呈现。

效果大家已经看过啦！就是图1所示的动画。

# example/01_esay/04_relu与二次拟合.py
# 4 开始训练
# 4.1 创建画布
fig = plt.figure(figsize=(15,4))
ax = fig.subplots(1,3,sharex=True,sharey=False)  # ax是包含一行三列，一共三块子画布的列表
# 4.2 训练，同时绘制动画
losses = []
for i in range(len(data_x)):
    x.set_value(data_x[i])
    label.set_value(data_label[i])
    loss.forward()
    for param in params:
        param.get_grad()
        param.update(lr=0.01)
    if i % 200 == 0:
        print(f'[{i}]:loss={loss.value},', [param.value for param in params])
    losses.append(loss.value)
    loss.clear()
    if i % 40 == 0:
        show_ax_mul(ax)  # 用于绘制多图动画

首先我们修改了 4、训练过程 部分的代码，创建画布，然后将画布对象传递给show_ax_mul()函数，绘制图像。在show_ax_mul()每次绘制完成后，调用plt.pause()让画面暂停下（否则画面会一闪而逝啥也看不清），然后清空画布方便下次绘图。

画布的绘制、清空都是在后台的，因此“清空画布”操作不会直接清空已经画出的函数图像。在下次绘制图像时，才会将原来的图像覆盖掉。

通过反复的绘制——清空，就形成了动画的效果。这样绘制的效率比较低，大家也可以自行搜索其它的动画绘制方法。

# example/01_esay/04_relu与二次拟合.py
def show_ax_mul(ax):
    '''
    用于绘制多图动画\n
	'''
    # 1 画真实的二次函数曲线
    show_x = np.linspace(-0.5, 2.5, 30, endpoint=True)
    show_y = [x_one * x_one for x_one in show_x]
    ax[2].plot(show_x, show_y)
    # 2 画模型拟合的曲线
    show_x = np.linspace(-0.5, 2.5, 10, endpoint=True)
    shows = {'add1':[], 'add2':[], 'mul1':[], 'mul2':[], 'y':[]}
    for x_one in show_x:
        x.set_value(x_one)
        add_21.clear()
        add_21.forward()
        shows['y'].append(add_21.value)
        shows['add1'].append(add_11.value)
        shows['add2'].append(add_12.value)
        shows['mul1'].append(mul_21.value)
        shows['mul2'].append(mul_22.value)
    ax[2].plot(show_x, shows['y'])
    ax[0].plot(show_x, shows['add1'])
    ax[0].plot(show_x, shows['add2'])
    ax[1].plot(show_x, shows['mul1'])
    ax[1].plot(show_x, shows['mul2'])
    y_0 = [0 for _ in show_x]  # 水平的参考线
    ax[2].plot(show_x, y_0)
    ax[0].plot(show_x, y_0)
    ax[1].plot(show_x, y_0)
    plt.pause(0.01)
    for i in range(ax.shape[0]):
        ax[i].cla()

4 补充：参数初始化的影响

参数的初始化对训练效果的影响真的很大！它可以影响训练的速度，最终成功拟合的方式，以及是否能够成功拟合。大家可以尝试着调整各个初始化参数的正负以及大小，观察它们对应训练效果的影响，并思考这样的影响是怎样产生的。

同时，由于我们的计算图还比较简单，也方便进行比较透彻的思考。

对比图7 与图8 的拟合结果，发现它们虽然有所区别，但是都较好的拟合了二次函数在[0, 2]的这一段曲线。这种区别是损失函数曲线中所无法体现出来的信息，这便是可视化的意义之一。

图8的训练迭代了1500次，而图7 迭代了10000次以上，两次训练的区别仅仅就是参数的初始化不同。随着计算图参数规模的增大，对应参数初始化的敏感程度会没有那么高。但利用不同的随机分布、不同的数值范围进行初始化，有时训练效果仍会有较大的差距。

# 图8对应的参数初始化
values = [-0.1571950013426796, -0.1070365984042347, 0.3791639008324807, 0.31960284774415215, 0.4263410176300597, 0.5097967360623379, 0.7597168751185974]
# 图7对应的参数初始化
values = [-0.4571950013426796, -0.4070365984042347, 0.3791639008324807, 0.31960284774415215, 0.4263410176300597, 0.5097967360623379, 0.7597168751185974]


图7：实际的拟合方式


图8：我期待的拟合方式

下节预告：计算图的封装

清风莫追

关注

48
点赞
踩
34

收藏

觉得还不错? 一键收藏
打赏
40
评论
【一起撸个深度学习框架】6 折与曲的相会——激活函数

但在实际遇到的问题中，输入与输出之间往往并不是简单的线性关系，它们之间的函数关系可能是二次的、指数、甚至分段的。此时”自适应线性单元“就不足以满足我们的需求了。而”激活函数“，将为计算图带来一种拟合这些非线性函数关系的能力。同时为了得到对于激活函数更加清晰和形象化的认知，本节我们还将使用matplotlib对拟合过程进行一些可视化的展现。
复制链接

扫一扫