前排提示:最五彩斑斓的一集

A
.
A.
A.
题意:求前9个数减去后8个数再+1的答案
c o d e : code: code:
#include <cstdio>
int a[15];
int b[10];
int main()
{
int asum=0;
int bsum=0;
for(int i=1;i<=9;i++) scanf("%d",&a[i]),asum+=a[i];
for(int i=1;i<=8;i++) scanf("%d",&b[i]),bsum+=b[i];
printf("%d",asum-bsum+1);
}
B . B. B.
题意:给两个大小一样的矩阵,问两个矩阵哪个位置的字符不一样,数据保证答案存在且唯一
c o d e : code: code:
#include <string>
#include <iostream>
#include <cstdio>
using namespace std;
int n;
char a[105][105],b[105][105];
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) cin>>a[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++) cin>>b[i][j];
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
{
if(a[i][j]!=b[i][j])
{
printf("%d %d",i,j);
return 0;
}
}
}
C . C. C.
题意:
分析:模拟题意即可,注意 2 A ∗ 2 2^A*2 2A∗2就是指数加1即可。
c o d e : code: code:
#include <cstdio>
const int N = 2e5+5;
int n;
int a[N];
int b[N];
int head;
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++) scanf("%d",&a[i]);
for(int i=1;i<=n;i++)
{
b[++head]=a[i];
if(head==1) continue;
while(b[head]==b[head-1])
{
b[head]=0;
head--;
b[head]++;
}
}
printf("%d",head);
}
D . D. D.
题意:给一个
H
∗
W
H*W
H∗W的二维矩阵,由.和#两种字符构成,如果
′
.
′
'.'
′.′的上下左右没有#,那么这个位置可以移动,求矩阵任意
′
.
′
'.'
′.′位置出发能搜索到的最多的
′
.
′
'.'
′.′的个数
数据范围
H
,
W
<
=
1000
H,W <=1000
H,W<=1000
分析:搜索+剪枝,重点是让每一个点只被搜索一次,从而保证复杂度为 O ( H ∗ W ) O(H*W) O(H∗W),具体实现可以把通常判断是否搜过的vis数组由0和1变为0和搜索编号,让能被同一个点出发搜到的所有点变成连通块,实现剪枝(说的抽象,可以看看代码), b f s bfs bfs或者 d f s dfs dfs都可以
c o d e : code: code:
#include <cstdio>
#include <queue>
#include <algorithm>
#include <iostream>
using namespace std;
const int N = 1005;
int h,w;
char mp[N][N];
bool b[N][N];
int dx[5]={0,0,1,-1};
int dy[5]={1,-1,0,0};
int ans,cnt;
struct node{
int x;
int y;
};
queue <node> q[N*N];
int num;
int vis[N][N];
void bfs(int x,int y)
{
num++;
q[num].push((node){x,y});
vis[x][y]=x*h+y;
while(!q[num].empty())
{
int fx=q[num].front().x;
int fy=q[num].front().y;
q[num].pop();
for(int i=0;i<4;i++)
{
int nx=fx+dx[i];
int ny=fy+dy[i];
if(nx<1||nx>h||ny<1||ny>w) continue ;
if(vis[nx][ny]==x*h+y) continue;
if(mp[nx][ny]=='.')
{
vis[nx][ny]=x*h+y;
cnt++;
}
if(b[nx][ny]) q[num].push((node){nx,ny});
}
}
int main()
{
scanf("%d%d",&h,&w);
for(int i=1;i<=h;i++)
for(int j=1;j<=w;j++)
{
cin>>mp[i][j];
}
for(int i=1;i<=h;i++)
for(int j=1;j<=w;j++)
{
if(mp[i][j]=='#') continue ;
int flag=1;
for(int k=0;k<4;k++)
{
int nx=i+dx[k];
int ny=j+dy[k];
if(nx<1||nx>h||ny<1||ny>w) continue;
if(mp[nx][ny]=='#')
{
flag=0;
break;
}
}
if(flag) b[i][j]=1;
}
ans=1;
for(int i=1;i<=h;i++)
for(int j=1;j<=w;j++)
{
if(!b[i][j]) continue ;
if(vis[i][j]) continue;//这里是剪枝的关键,只把没搜过的点进行搜索
cnt=1;
bfs(i,j);
ans=max(ans,cnt);
}
printf("%d",ans);
}
E . E. E.
题意:给 N N N个点的坐标, P i Pi Pi每次移动可以从 ( X i , Y i ) (Xi,Yi) (Xi,Yi)到 ( X i + 1 , Y i + 1 ) , ( X i + 1 , Y i − 1 ) , ( X i − 1 , Y i + 1 ) , ( X i − 1 , Y i − 1 ) (Xi+1,Yi+1),(Xi+1,Yi-1),(Xi-1,Yi+1),(Xi-1,Yi-1) (Xi+1,Yi+1),(Xi+1,Yi−1),(Xi−1,Yi+1),(Xi−1,Yi−1)四个方向,定义 d i s t ( A , B ) dist(A,B) dist(A,B)为从 A A A点到 B B B点的最小移动次数,若不能从 A A A到 B B B,则 d i s t ( A , B ) = 0 dist(A,B) = 0 dist(A,B)=0,求任意两点之间的 d i s t dist dist的和[ Σ i = 1 N − 1 \Sigma_{i=1}^{N-1} Σi=1N−1 Σ j = i + 1 N \Sigma_{j=i+1}^{N} Σj=i+1N d i s t ( P i , P j ) dist(Pi,Pj) dist(Pi,Pj)]
分析:
先考虑任给两个点,这两个点能否相互到达。题意说明是斜着四十五度进行移动,即如图所示,红色可以互相到达,白色可以互相到达,不能从红到白或者从白到红。
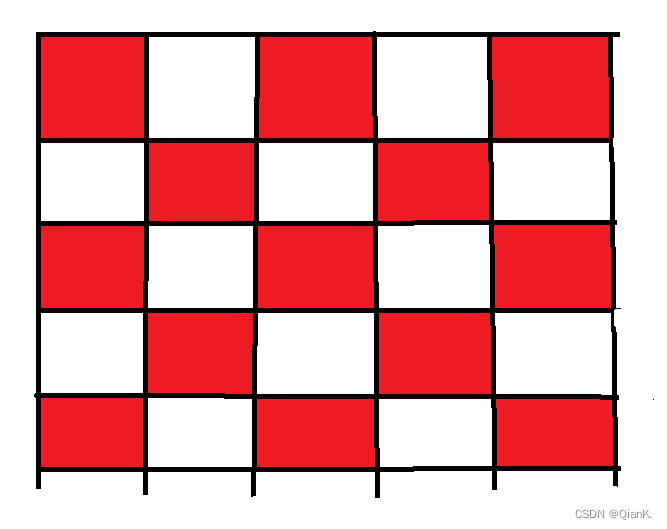
那么我们不难发现,横纵坐标和为偶数的可以相互到达,和为奇数的可以相互到达,所以分成两组统计答案即可,不同组之间的坐标的
d
i
s
t
dist
dist都是0.
斜着移动太费劲了,不如把每个点的坐标都旋转45°然后把距离乘以
2
\sqrt2
2,同时把每次移动也这样变化(可以把每次移动看成一段向量,对向量进行旋转和放大),坐标从
(
X
,
Y
)
(X,Y)
(X,Y)变化为
(
X
+
Y
,
X
−
Y
)
(X+Y,X-Y)
(X+Y,X−Y),移动变成从
(
a
,
b
)
(a,b)
(a,b)移动至
(
a
+
2
,
b
)
,
(
a
−
2
,
b
)
,
(
a
,
b
+
2
)
,
(
a
,
b
−
2
)
(a+2,b),(a-2,b),(a,b+2),(a,b-2)
(a+2,b),(a−2,b),(a,b+2),(a,b−2),因为答案只考虑移动次数,所以将坐标和移动同时旋转放大不会影响答案,这样就把斜着移动转为上下左右移动了。考虑
d
i
s
t
(
A
,
B
)
=
1
/
2
∗
(
∣
X
a
−
X
b
∣
+
∣
Y
a
−
Y
b
∣
)
dist(A,B)=1/2*(|Xa-Xb|+|Ya-Yb|)
dist(A,B)=1/2∗(∣Xa−Xb∣+∣Ya−Yb∣),即曼哈顿距离的一半。
下面考虑把这个数学式子化简一下,只考虑求
Σ
i
=
1
n
−
1
\Sigma_{i=1}^{n-1}
Σi=1n−1
Σ
j
=
i
+
1
n
\Sigma_{j=i+1}^{n}
Σj=i+1n
∣
X
i
−
X
j
∣
|Xi-Xj|
∣Xi−Xj∣,首先把
X
X
X升序排列,然后直接去掉绝对值,原式变为
Σ
i
=
1
n
−
1
\Sigma_{i=1}^{n-1}
Σi=1n−1
Σ
j
=
i
+
1
n
\Sigma_{j=i+1}^{n}
Σj=i+1n
(
X
i
−
X
j
)
(Xi-Xj)
(Xi−Xj)
X i 对答案的贡献 = 比他小的 X 的个数 ∗ X i − 比他大的 X 的个数 ∗ X i Xi对答案的贡献=比他小的X的个数*Xi-比他大的X的个数*Xi Xi对答案的贡献=比他小的X的个数∗Xi−比他大的X的个数∗Xi。
这样就可以 O ( N ) O(N) O(N)地统计答案,排序复杂度 O ( N l o g N ) O(NlogN) O(NlogN),总复杂度 O ( N l o g N ) O(NlogN) O(NlogN),对 Y Y Y的贡献同理可求,不要忘记最后答案 ∗ 1 / 2 *1/2 ∗1/2
c o d e : code: code:
#include <cstdio>
#include <algorithm>
#define int long long
using namespace std;
const int N = 2e5+5;
int n;
int h1,h2;
int a1[N],a2[N],a3[N],a4[N];
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
int x,y;
scanf("%lld%lld",&x,&y);
if((x+y)%2)
{
a1[++h1]=(x+y);
a2[h1]=(x-y);
}
else
{
a3[++h2]=(x+y);
a4[h2]=(x-y);
}
}
int ans=0;
sort(a1+1,a1+h1+1);
sort(a2+1,a2+h1+1);
sort(a3+1,a3+h2+1);
sort(a4+1,a4+h2+1);
for(int i=1;i<=h1;i++)
{
int cnt=a1[i];
ans+=(i-1)*cnt;
ans-=(h1-i)*cnt;
}
for(int i=1;i<=h1;i++)
{
int cnt=a2[i];
ans+=(i-1)*cnt;
ans-=(h1-i)*cnt;
}
for(int i=1;i<=h2;i++)
{
int cnt=a3[i];
ans+=(i-1)*cnt;
ans-=(h2-i)*cnt;
}
for(int i=1;i<=h2;i++)
{
int cnt=a4[i];
ans+=(i-1)*cnt;
ans-=(h2-i)*cnt;
}
printf("%lld",ans/(2LL));
}
F
.
F.
F.
传送门
题意:求 Σ i = 1 N \Sigma_{i=1}^{N} Σi=1N Σ j = i + 1 N \Sigma_{j=i+1}^{N} Σj=i+1N m a x ( A j − A i , 0 ) max(Aj-Ai,0) max(Aj−Ai,0),数据规模 N < = 2 e 5 N<=2e5 N<=2e5
分析:拿人话说一下,就是统计每个 A i Ai Ai后边所有比他大的数,并把两者的差值计入答案。
看到这种分大小关系统计答案的题目,一般考虑排序。
考虑每个
A
i
Ai
Ai对答案的影响
A
i
的贡献
=
A
i
前面比他小的
A
的个数
∗
A
i
−
A
i
后面比他大的
A
的个数
∗
A
i
Ai的贡献=Ai前面比他小的A的个数*Ai-Ai后面比他大的A的个数*Ai
Ai的贡献=Ai前面比他小的A的个数∗Ai−Ai后面比他大的A的个数∗Ai
我们把每个
A
i
Ai
Ai的贡献求和就是答案。
我们开一个新数组 B [ N ] B[N] B[N],初始值为 0 0 0。先把最小的 A i Ai Ai找到,然后把 B i Bi Bi改为1,接着再找第二小的 A i Ai Ai,然后把 B i Bi Bi改为1。。。一共进行 N N N次操作。第 K K K次操作时, B B B数组已经有了 K − 1 K-1 K−1个 1 1 1,这些 1 1 1代表他们对应的 A A A比当前的 A j Aj Aj要小,剩下的 0 0 0代表的 A A A都比当前 A j Aj Aj要大。进而,我们只需要统计 A i Ai Ai前面的 1 1 1的总数和 A i Ai Ai后边的 0 0 0的总数即可。
具体到代码实现,对每次操作,我们先统计0和1的数量,再把当前位置的 B B B改为1。用单点修改的线段树可以很好实现上述过程,统计和修改的单次时间复杂度都是 O ( l o g N ) O(logN) O(logN),总的时间复杂度为 O ( N l o g N ) O(NlogN) O(NlogN)
再优化一下,第 i i i次操作求后边的 0 0 0的个数时,可以直接用公式:
s u m ( 0 ) = N − i − ( n o w p l − 1 − s u m ( 1 ) ) sum(0) = N-i-(nowpl-1-sum(1)) sum(0)=N−i−(nowpl−1−sum(1))
其中, n o w p l nowpl nowpl表示 A i Ai Ai的下标, s u m ( 1 ) sum(1) sum(1)表示该位置前面 1 1 1的总数
c o d e : code: code:
#include <cstdio>
#include <algorithm>
#include <iostream>
#define int long long
using namespace std;
const int maxn = 4e5+5;
int n,m,p;
int a[maxn];
int c[maxn];
struct node{
int l,r,tag,sum;
};
struct snode{
int num;
int pl;
};
snode b[maxn];
node tree[maxn<<2];
int ls(int rt)
{
return rt<<1;
}
int rs(int rt)
{
return rt<<1|1;
}
void pushdown(int rt)
{
if(tree[rt].tag)
{
int tg=tree[rt].tag;
tree[rt].tag=0;
tree[ls(rt)].tag +=tg;
tree[rs(rt)].tag +=tg;
tree[ls(rt)].sum +=(tg*(tree[ls(rt)].r-tree[ls(rt)].l+1));
tree[rs(rt)].sum +=(tg*(tree[rs(rt)].r-tree[rs(rt)].l+1));
return ;
}
}
void build(int rt,int l,int r)
{
tree[rt].l=l;tree[rt].r=r;
if(l==r)
{
tree[rt].sum=a[l];
return ;
}
int mid=(l+r)>>1;
build(ls(rt),l,mid);
build(rs(rt),mid+1,r);
tree[rt].sum=tree[ls(rt)].sum+tree[rs(rt)].sum;
}
int s_search(int rt,int l,int r)
{
if(tree[rt].l>=l&&tree[rt].r<=r) return tree[rt].sum;
int s=0;
pushdown(rt);
if(tree[ls(rt)].r>=l) s+=s_search(ls(rt),l,r);
if(tree[rs(rt)].l<=r) s+=s_search(rs(rt),l,r);
tree[rt].sum=tree[ls(rt)].sum+tree[rs(rt)].sum;
return s;
}
void add(int rt,int l,int r,int k)
{
if(tree[rt].l>=l&&tree[rt].r<=r)
{
tree[rt].tag+=k;
tree[rt].sum+=(tree[rt].r-tree[rt].l+1)*k;
return ;
}
pushdown(rt);
if(tree[ls(rt)].r>=l) add(ls(rt),l,r,k);
if(tree[rs(rt)].l<=r) add(rs(rt),l,r,k);
tree[rt].sum=tree[ls(rt)].sum+tree[rs(rt)].sum;
return ;
}
bool cmp(snode a,snode b)
{
return a.num<b.num;
}
signed main()
{
scanf("%lld",&n);
for(int i=1;i<=n;i++)
{
scanf("%lld",&c[i]);
b[i].num=c[i];
b[i].pl=i;
}
sort(b+1,b+1+n,cmp);
build(1,1,n);
int ans=0;
for(int i=1;i<=n;i++)
{
int nowpl=b[i].pl;
int nowx=s_search(1,1,nowpl);
int nowy=n-i-(nowpl-1-nowx);
ans+=nowx*b[i].num;
ans-=nowy*b[i].num;
}
printf("%lld",ans);
}






















 175
175











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








