A. Destroying Bridges 题意:一个人住在1号岛屿,一共有n个岛屿,并且一共有 题解:只看1号岛屿就可以,一共1号岛屿有n - 1条边,如果 代码: #include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
const int mod = 998244353 ;
inline ll read() {
ll x = 0, f = 1 ;
char c = getchar() ;
while (c > '9' || c < '0') {
if (c == '-')
f = -1 ;
c = getchar() ;
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , d , k , a[maxn] ;
void solve(){
n = read() ;
k = read() ;
if(k >= n - 1){
cout << 1 << endl ;
}
else{
cout << n << endl ;
}
}
int main(){
t = read() ;
while(t --){
solve() ;
}
return 0 ;
}B. Equal XOR 题意:给你2 * n个数字,这些数字必须满足 题解:因为这些数字都是小于等于n,所以如果没有重复的情况那么就是1~n每个数字各一个,那很简单,想要取多少个数字那么就将数组排序,依次取即可,异或和一定相等。那么如果说有相同的情况呢,那么也很容易想了,先把a[1~n]和a[n + 1 ~ 2 * n]的数字统计一下,然后枚举,如果说两个数组都有这个数字,那么就放在前面,如果说只有一个数组有的数字,就放到最后面。为什么是对的呢,因为题目中说答案一定存在,那么每次取都是2的倍数,这样从前面取的数字一定是两个数组中都有的,那么两个数组一定相等,那如果取到单个数组中有的数字,那么一定是偶数个,那偶数个异或的值是0,意思也就是这个数组会添加一个0,另一个数组也是0,不会影响答案。所以一定符合答案。 代码: #include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
const int mod = 998244353 ;
inline ll read() {
ll x = 0, f = 1 ;
char c = getchar() ;
while (c > '9' || c < '0') {
if (c == '-')
f = -1 ;
c = getchar() ;
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
ll t , n , k , a[maxn] , b[maxn] , c[maxn] , d[maxn] ;
void solve(){
n = read() ;
k = read() ;
ll ans ;
map < ll , ll > mp , mq ;
for(int i = 1 ; i <= n ; i ++){
a[i] = read() ;
mp[a[i]] ++ ;
}
for(int i = 1 ; i <= n ; i ++){
b[i] = read() ;
mq[b[i]] ++ ;
}
ll cnt = 0 , Cnt = 0 ;
ll res = n , Res = n ;
for(int i = 1 ; i <= n ; i ++){
while(1){
if(mp[i] == 0 || mq[i] == 0)
break ;
c[++ cnt] = i ;
d[++ Cnt] = i ;
mp[i] -- ;
mq[i] -- ;
}
while(1){
if(mp[i] == 0){
break ;
}
c[res] = i ;
res -- ;
mp[i] -- ;
}
while(1){
if(mq[i] == 0){
break ;
}
d[Res] = i ;
Res -- ;
mq[i] -- ;
}
}
for(int i = n ; i >= n - 2 * k + 1 ; i --){
cout << c[i] << " " ;
}
cout << endl ;
for(int i = n ; i >= n - 2 * k + 1 ; i --){
cout << d[i] << " " ;
}
cout << endl ;
}
int main(){
t = read() ;
while(t --){
solve() ;
}
return 0 ;
}C. MEX Game 1 题意:Alice和Bob在玩一个游戏,给你一个数组a,Alice和Bob每次从中取出一个数组,Alice先操作,Alice每次可以取一个数字加入数组C,Bob每次取出一个数字删除,问两个人的策略都是最优的,最终答案的Mex最大是多少。(Mex值是指未出现的最小自然数) 题解:这个题是我最先做出来的,简单的博弈论,有可能一开始毫无头绪,但是你想,如果一个数字有2个或者以上,那么Bob扔掉a[i] - 1个,Alice只要在最后的时刻选择它,那么这个数字一定存在,这与轮数没有关系,所以说,影响答案的只有单个数字的时候,很明显,要求Mex值,需要尽量小的数字,所以说很容易想到,将只有一个的数字取出,然后排序,Alice和Bob分别操作,Alice拿一个,Bob扔一个,最后用 代码: #include<bits/stdc++.h>
using namespace std ;
typedef long long ll ;
const int maxn = 1e6 + 7 ;
const int mod = 998244353 ;
inline ll read() {
ll x = 0, f = 1 ;
char c = getchar() ;
while (c > '9' || c < '0') {
if (c == '-')
f = -1 ;
c = getchar() ;
}
while (c >= '0' && c <= '9') {
x = x * 10 + c - '0' ;
c = getchar() ;
}
return x * f ;
}
bool vis[maxn] ;
ll t , n , d , k , a[maxn] , b[maxn] , sum[maxn] , Sum[maxn] ;
void solve(){
int cnt = 0 ;
memset(vis , 0 , sizeof(vis)) ;
n = read() ;
map < ll , ll > mp ;
for(int i = 1 ; i <= n ; i ++){
a[i] = read() ;
mp[a[i]] ++ ;
}
for(auto it : mp){
if(it.second == 1){
b[++ cnt] = it.first ;
}
}
sort(b + 1 , b + cnt + 1) ;
for(int i = 2 ; i <= cnt ; i += 2){
vis[b[i]] = 1 ;
}
sort(a + 1 , a + n + 1) ;
ll nn = unique(a + 1 , a + n + 1) - a - 1 ;
int rt = 1 ;
ll Mex = 0 ;
while(mp[Mex] && vis[Mex] == 0){
Mex ++ ;
}
cout << Mex << endl ;
}
int main(){
t = read() ;
while(t --){
solve() ;
}
return 0 ;
}注:B题也许有更优的做法,如果有更好的做法希望大家踊跃指出,谢谢啦! 喜欢作者的记得点赞收藏加关注哦~
 条边连接着各个岛屿,问用最优的方式删除k条边,你从1号岛屿最少能去多少个岛屿(包含自己)。
条边连接着各个岛屿,问用最优的方式删除k条边,你从1号岛屿最少能去多少个岛屿(包含自己)。 ,那么只能到达自己,其他情况n个岛屿均可到达。
,那么只能到达自己,其他情况n个岛屿均可到达。 ,你必须选择两个集合l和r,l要从1~n中选择2 * k个数字,l必须是a[1~n]的子集,r也同理,子集的定义是指从a[1 ~ n]中删除y个数字,其他数字任意排列的组合,问能否使l集合中的所有数字异或和等于r集合中所有数字的异或和。
,你必须选择两个集合l和r,l要从1~n中选择2 * k个数字,l必须是a[1~n]的子集,r也同理,子集的定义是指从a[1 ~ n]中删除y个数字,其他数字任意排列的组合,问能否使l集合中的所有数字异或和等于r集合中所有数字的异或和。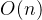 的复杂度统计出Mex值就是最终的答案。复杂度
的复杂度统计出Mex值就是最终的答案。复杂度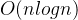

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










