回溯算法实现NPC旅行售票员问题

 问题重述：

设有n个城镇，已知每两个城镇之间的距离，一个售货员从某一城镇出发巡回售货，问这个售货员应如何选择路线，能使每个城镇经过一次且仅一次，最后返回到出发地，而使总的费用最少？

如图所示：

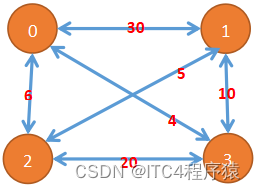
注：图中各边所标注的数值为经过各边所需要花费的代价，我们假设起点为0。

问题分析 ：

算法的选择

本题是一个典型的NPC问题。在刚看到这个问题的时候我也不确定用什么算法去解决它比较好，可不可以使用贪心算法呢？可以不可以使用动态规划算法呢？

贪心算法是否可行

假设本问题可以采用贪心算法，那么可以使用的贪心策略是选择最短边，经过的节点排除在外（起点除外），那么我们来看是否符合使用条件。

贪心算法如果可以使用，必须要满足最优子结构的性质，即原问题的最优解可以由子问题的最优解推导出来，我们规定d(i)为当前节点标号为i时到最后一个没有经过的城镇的最小代价的路径。如果满足最优子结构，则d(i)=min{d(a),d(b),d(c)......}+Mi(选择出来的最优节点到i节点的距离)，但是呢，这不一定正确，如果存在一个节点m,d(m)此时是最优的，但是呢，d(m)+Mm却不是最优的，所以最优子结构无法满足。

贪心算法笼统来说就是将大问题分成无数个子问题，如果每个子问题都能充分最优，那么便能实现整体的最优，注意这里说的是充分的最优，而不是对于每个子问题来说达到最优即可。0-1背包问题为什么不能用贪心算法，是因为如果用贪心算法可能会存在空闲的空间，那部分空间的价值就被浪费了，所以总体达到的解未必是全局最优解。而经典的背包问题则必定能填满所有的背包空间，便不存在剩余问题未解决的问题了。

综上所述呢，贪心算法对于该问题的求解来说是行不通的。

动态规划是否可行

那么问题来了贪心算法不行的话，动态规划是否可以求解呢？

答案依然是否定的，因为由上可以知道，最优子结构的性质无法满足，动态规划算法也就行不通了。

动态规划是广义的贪心算法，但是也必须要满足最优子结构的性质才能保证解的正确性。

选择回溯算法解决本问题

回溯是一种高效率的穷举方法，之所以选择回溯方法，是因为贪心算法和动态规划都无法使用的情况下，我们能使用的最方便的算法便是穷举算法了，但是穷举算法往往都是伴随着高阶的时间复杂度与空间复杂度，而且有许多本不必要继续执行的操作会拖累算法整体的执行效率。而回溯法则很好的解决了这个问题，搭配上合适的约束函数与剪枝函数，我们可以有效的提高穷举的效率。回溯法的广泛的适用性是我们选择回溯算法求解本问题的原因。

经验之谈~~ 不能贪心，也不能动态，那就回溯吧。哈哈~~多么痛的领悟

接下来该来解决这个老大难的问题了。 

问题解决 

 算法框架

对于我们这个问题呢，我们先来建立我们的解空间树，及所有可能的解构成的解空间树。大概是这样的，嗯。。。只能画成这样了。

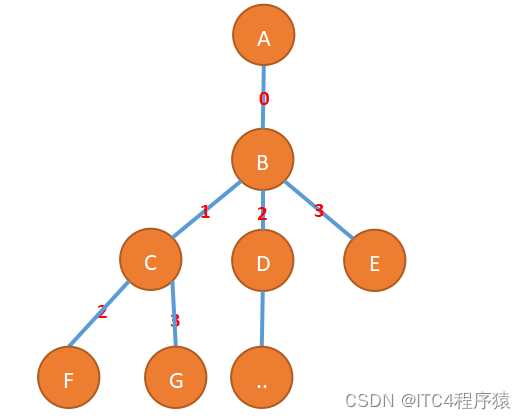
然后呢我们的思路就是去用回溯法递归遍历这个排列树，层层遍历。

递归算法代码如下：

void backTrack(int t,int n){
    //其中的t代表的是当前遍历到的层数，层数从0开始
    if(t >= n){
        return;
    }
    else
    {
        //k取值到n-1结束是因为节点从0号节点开始
        for(int k = t; k < n; k++){
            swap(x[t], x[k]);
            //cut()为剪枝函数，bound()为约束函数
            if(cut()&&bound()) backTrack(t + 1, n);//递归到下一层
            swap(x[t], x[k]);//回溯回原来的状态
        }
    }
}

整体求解代码

有了递归函数以后，我们就基本上求解出了问题的关键，接下来是整体的代码。

#include <iostream>

#define MAX_SIZE 5
#define POINT_NUM 4

using namespace std;

int bestCost;
int bestPath[MAX_SIZE] = { 0,1,2,3,0 };
int allPath[][POINT_NUM] = { { -1, 30, 6, 4},{30, -1, 5, 10},{6, 5, -1, 20},{4, 10, 20, -1} };


//初始化函数
void initialize() {
	bestCost = 10000;
}

//约束函数
bool bound() {
	return true;
}

//剪枝函数
bool cut(int nowCost) {
	if (nowCost >= bestCost) {
		return false;
	}
	return true;
	
}

//计算当前花费
int countCost(int t) {
	int cost = 0;
	for (int i = 0; i < t; i++) {
		cost += allPath[bestPath[i]][bestPath[i + 1]];
	}
	return cost;
}

//打印结果函数
void print() {
	cout << "最优代价为：" << bestCost << endl;
	cout << "最优路径为：";
	for (int i = 0; i < MAX_SIZE; i++) {
		if (i) cout << " -> ";
		cout << bestPath[i];
	}
	cout << endl;
}

//递归函数
void backTrack(int t,int n) {
	if (t >= n) {
		bestCost = countCost(n - 1) + allPath[bestPath[MAX_SIZE - 2]][bestPath[MAX_SIZE - 1]];
		print();
		return;
	}
	else 
	{
		for (int k = t; t < n; t++) {
			swap(bestPath[t], bestPath[k]);
			int nowCost = countCost(t);
			if (cut(nowCost) && bound()) {
				backTrack(t + 1, n);
			}
			swap(bestPath[t], bestPath[k]);
		}
	}
}

void swap(int &a,int &b) {
	int temp = a;
	a = b;
	b = temp;
}

int main() {
	//初始化
	initialize();
	//调用递归函数
	backTrack(1, POINT_NUM);
}

其中allPath为边长矩阵。

运行结果如下：

最优代价为：59
最优路径为：0 -> 1 -> 2 -> 3 -> 0
最优代价为：25
最优路径为：0 -> 2 -> 1 -> 3 -> 0

我们可以得到最优解与最短路径，至此本题求解已结束。

创作不易，请大家点点赞呀，呜呜呜~~谢谢大家支持~~