目录
快速选择,第k小数|快排
给定包含n个元素的整型数组,编写时间复杂度为O(n)的算法,求得数组中第k (k<n)小的数。
//减治法
//可以画数组帮助理解;
//将数组中k个最小的元素全部输出:
//找到第k小的元素B后,再扫描一遍数组,输出数组中小于等于B的元素即可,时间代价O(n)
int QuickSelect(int R[],int m, int n, int k){
int j=Partition(R, m, n);
int nL=j-m; //左部分元素个数
if(nL==k-1) return R[j];
// 每次只要去找左部分/右部分;
else if(nL>k-1) //在左部分找第k小数
return QuickSelect(R,m,j-1,k);
else //在右部分找第k-nL-1小数
return QuickSelect(R, j+1, n, k-nL-1);
}
int QuickSelect(int R[],int m, int n, int k){
int j, nL;
while(true){
j=Partition(R, m, n);
nL=j-m; //左部分元素个数
if(nL==k-1) return R[j];
else if(nL>k-1) n=j-1; //在左部找第k小数
else m=j+1,k=k-nL-1; //在右部找第k-nL-1小数
}
}
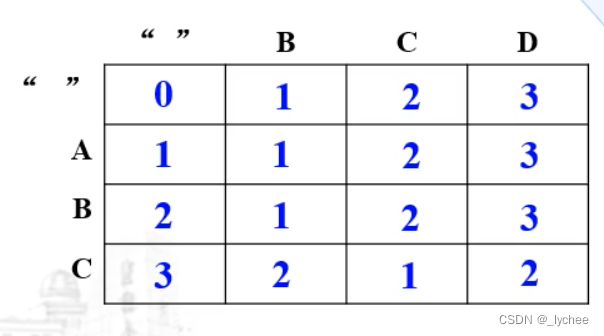
字符串编辑距离| DP

1: 若S[M]=P[N],Dist(m,n)=(m-1,n-1);
2: 若S[M]!=P[N], 第一种:Dist(m,n)=D(m-1,n-1)+1;
第二种: Dist(m,n)=D(m,n-1)+1; //插入P[N]
第三种:D(m,n)=D(m-1,n)+1;//删除S[N]
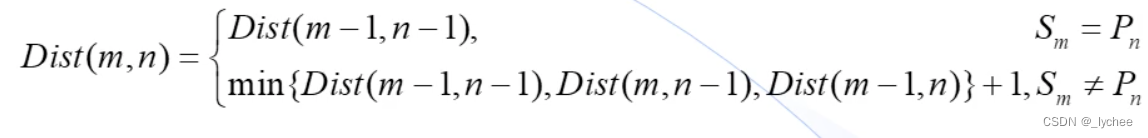
大于等于K的第一个位置
对半查找;注意结束的时候 high<slow;high是小于等于k的最后一个位置;slow
// 找大于等于k的第一个元素
int BinarySearch(int R[],int n, int K){
//在R中对半查找K,R中关键词递增有序
int s = 1, e = n, mid;
while(s <= e){
mid=(s+e)/2;
if(K<=R[mid]) e=mid-1; //在左半部分查找
else s=mid+1; //K>R[mid],在右半部分查找
}
return slow;
}
//找小于等于k的最后一个元素
int BinarySearch(int R[],int n, int K){
//在R中对半查找K,R中关键词递增有序
int s = 1, e = n, mid;
while(s <= e){
mid=(s+e)/2;
if(K<=R[mid]) e=mid-1; //在左半部分查找
else s=mid+1; //K>R[mid],在右半部分查找
}
return high;
}
求数组中逆序对的个数
//暴力解法是0(mn)
id Merge(int R[],int low, int mid, int high){
/*将两个相邻的有序数组(Rlow,Rlow+1,…,Rmid)和(Rmid+1,Rmid+2,…,Rhigh)合并成一个有序数组*/
int i=low, j=mid+1, k=0, cnt=0;
int *X=new int[high-low+1];
while(i<=mid && j<=high)
if(R[i]<=R[j]) X[k++]=R[i++];
else X[k++]=R[j++], cnt+=mid-i+1;
while(i<=mid) X[k++]=R[i++]; //复制余留记录
while(j<=high) X[k++]=R[j++];
for(int k=0,i=low; i<=high; i++,k++) //将X拷贝回R
R[i]=X[k];
delete []X;
return cnt;
}
void MergeSort(int R[], int m, int n){
if(m < n){
int k = (m+n)/2;
MergeSort(R, m, k);
MergeSort(R, k+1, n);
Merge(R, m, k, n);
}
}链表的归并排序
ListNode* sortList(ListNode* head, ListNode* tail) {
if (head == nullptr) {
return head;
}
if (head->next == tail) {
head->next = nullptr;
return head;
}//只有一个结点
ListNode* slow = head, *fast = head;
while (fast != tail) {
slow = slow->next;
fast = fast->next;
if (fast != tail) {
fast = fast->next;
}
}
ListNode* mid = slow->next;
slow->next=NULL;
return merge(sortList(head, mid), sortList(mid, tail));
}
ListNode* merge(ListNode* head1, ListNode* head2) {
ListNode* dummyHead = new ListNode(0);//新建一个链表
ListNode* temp = dummyHead, *temp1 = head1, *temp2 = head2;
while (temp1 != nullptr && temp2 != nullptr) {
if (temp1->val <= temp2->val) {
temp->next = temp1;
temp1 = temp1->next;
} else {
temp->next = temp2;
temp2 = temp2->next;
}
temp = temp->next;
}
if (temp1 != nullptr) {
temp->next = temp1;
} else if (temp2 != nullptr) {
temp->next = temp2;
}
return dummyHead->next;
}
判断有向图是否存在回路/成环:拓扑排序/dfs
struct Edge{
int Veradj;
Edge* link;
};
struct Vertex{
int Vername;
Edge* adjacent;
};
void Indegree(Vertex Head[],int n, int count[] ){
for(int i =1;i<= n;i++)
count[i]=0;//将每个点的入度 初始化为0
for(int i=0;i<=n;i++){
for(Edge* p=Head[i].adjacent;p;p=p->link){
count[p->Veradj]++; //遍历所有的边,讲每条边对应顶点的入度+1
}
}
}
void Topo(int n,Vertex Head[] ){
int count[N];
stack<int> s;//用队列也可以
Indegree(Head,n,count);//求每个点的入度
for(int i=1;i<=n;i++) if(count[i]==0) s.push(i);
for(int i=1;i<=n;i++){
if(s.empty()) return false;//在n内找不到入度为0的点 说明有环;
int k=s.top();
s.pop();//出栈表示该事件执行,被该活动约束的下一个活动可以改变状态;
for(Edge* p=Head[k].adjacent;p;p=p->link){
count[p->Veradj]--;
if( count[p->Veradj]==0) s.push(p->Veradj);
}
}
return true;
}
//拓展 数组实现栈
//利用count 的闲置空间,存储入度为0 的点
void Topo(int n,Vertex Head[] ){
int count[N];
int top=-1;//指向上一个入度为0的节点下标;
Indegree(Head,n,count);//求每个点的入度
for(int i=1;i<=n;i++) if(count[i]==0) {
count[i]=top;
top=i;
}
for(int i=1;i<=n;i++){
if(top==-1) return false;//top为-1,表示在n内找不到入度为0的点 说明有环;
int k=top;
top=count[top];//更新top,相当于弹栈
for(Edge* p=Head[k].adjacent;p;p=p->link){
count[p->Veradj]--;
if( count[p->Veradj]==0){
count[k]=top;
top=k;//相当于压栈
}
}
}
return true;
}
int DFS(int u, int start)// start 是u的上一个路径结点
{
int i;
visited[u] = -1;
path[u] = start;
for (i = 0; i < n;i++)
{
//start->u->i ;
if (G[u][i]&&i!=start)// i!=start 即满足 非1->0->1模式
{
if (visited[i]<0)//该结点在路径中,存在回路
{
count++;
return 0;
}
if (!DFS(i,u))// 对i进行深搜,i的前驱是u;
return 0;
}
}
visited[u] = 1;
return 1;
}拓展: 逆拓扑序列;关键路径
//拓扑图:从一个源点v出发,经过所有的点和边,到达汇点
//逆拓扑排序
void DFS_TopoSort(Vertex*Head, int v, int vis[]){
vis[v]=1; //访问顶点v
Edge* p= Head[v].adjacent;
while(p!=NULL){
if(vis[p->VerAdj]==0)
DFS_TopoSort(Head,p->VerAdj,vis);
p=p->link; }
printf(“%d ”,v); //该点深搜结束再访问该结点
//此处不要求回溯找所有边,只需遍历所有点
}
void VertexEarliestTime(Vertex Head[],int n, int ve[]){//一定要按照拓扑序列访问
//计算顶点的最早发生时间
for(int i=1;i<=n;i++)
ve[i]=0;//初始化为0
//遍历所有边;按约束条件,更新从源点到各点的最长路径
for(int i=1;i<=n;i++) //按拓扑序计算各顶点最早发生时间
for(Edge* p=Head[i].adjacent; p!=NULL; p=p->link){
int k=p->VerAdj;
if(ve[i]+p->cost>ve[k])
ve[k]=ve[i]+p->cost;
}
}
判断单链表中是否成环,求环的入口(不考)
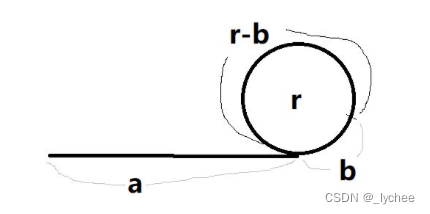
思路:
先利用快慢指针判断是否成环,快指针走两步、满指针走一步。
若快慢指针相遇,说明成环。否则fast->next为空,说明链表不成环。
然后利用慢指针走的快指针的一半路,可以得到:2(a+b)=a+nr+b 推出 a=nr-b=r(n-1)+r-b;
即此次第二个慢指针从head出发会与第一个slow在环的入口处相遇。
Node find(){
Node meet = null;
while (faster.next != null && faster.next.next != null) {
faster = faster.next.next;
slower = slower.next;
if (faster == slower) {
meet = faster;
break;
}
}
if (meet != null) {
newSlower = head;
while (newSlower != slower) {
newSlower = newSlower.next;
slower = slower.next;
}
return newSlower;
}
return null;
}判断单链表是否是回文**
回文串是对称的,即链表的中间结点左右都是相同的。只需遍历到中间结点,对链表中间结点前的部分进行反转,然后再从中间结点向两边遍历,如果一样,那么就说明链表两边是对称的,即是该链表是回文链表了。
因此这里首先是要找到中间结点,找中间结点最简单的方法是用一对快慢指针,初始化指向第一个结点,慢指针步长为1,快指针步长为2,如果链表长度为偶数,中间结点是不存在的,那么当快指针遍历到末尾(NULL)时,说明慢指针遍历到了第n/2+1个结点(n为链表长度);如果链表长度为奇数,那么当快指针指向的结点的下一个结点为NULL时,说明慢指针遍历到了中间结点。
因此,如果是奇数,以1->2->3->2->1为例,反转中间结点以前的部分,即是1<-2和3->2->1,这时候进行比较的时候就应该从中间结点的下一个结点开始比较1<-2和2->1是否一样即可; 如果是偶数, 以1->2->3->3->2->1为例,反转中间结点以前的部分,即是1<-2<-3和3->2->1,此时直接比较两边即可。
参考链接:https://blog.csdn.net/qq_28114615/article/details/84024283
bool isPalindrome(ListNode* head) {
if(!head)return true;
ListNode* PreNode=NULL; //指向前一个结点
ListNode* NextNode=head->next; //指向下一个结点
ListNode* CurNode=head; //指向当前结点(慢指针)
ListNode* Fast=head; //快指针
while(Fast!=NULL&&Fast->next!=NULL) //链表长度为奇数时Fast->next==NULL,为偶数时Fast==NULL
{
Fast=Fast->next->next; //步长为2
NextNode=CurNode->next; //先指向下一个结点
CurNode->next=PreNode; //当前结点回指前一个结点实现反转
PreNode=CurNode; //反转结束后当前结点作为下一次的前一个结点
CurNode=NextNode; //反转结束后下一个结点作为下一次的当前结点
}
if(Fast!=NULL&&Fast->next==NULL)CurNode=CurNode->next; //链表长度为奇,反转后当前结点需先指向下一个结点
while(PreNode!=NULL) //链表两侧进行比较
{
if(PreNode->val!=CurNode->val)return false;
else
{
CurNode=CurNode->next;
PreNode=PreNode->next;
}
}
return true;
}
快速幂
//快速幂
double pow(double a, long long n){//递归求a^n
if(n==0) return 1;
double b=pow(a ,n/2);//递归求a^n/2
double ans=b*b;
if(n%2==1) ans*=a;
return ans;
}利用先根和中根重建二叉树;
//先序序列区间 [preL,preR],中序序列 [inL,inR]
//先确定根结点
//利用先根序列的首结点在中根的位置,可以把子结点划分成左右两部分
//分别递归构建根结点的左右孩子
node* Create(int preL,int preR,int inL,int inR){
if(preL>preR) return NULL;//
node* root=new node;
root->data=pre[preL];//当前根节点的值
for(int k=inL,k<=inR;i++){
if(in[k]==pre[preL]) break;//找到中序遍历的根结点位置 ,划分左右孩子
}
int numleft=k-inL;
root->lchild=Create(preL+1,preL+numleft,inL,k-1);
root->rchild=Create(preL+numleft+1,preR,k+1,inR );
return root;
}
KMP / next 数组
扩展应用
➢第二长相等的前后缀长度:next[next[n]].
➢最长重复前缀:next数组中的最大值maxi(next[i]).
void buildNext(char *P,int next[]){
int m=strlen(P);
next[0]=-1;
int j=0, k=-1; //k=next[j]
while(j<m-1){
if(k==-1 || P[k]==P[j])
j++,k++,next[j]=k;
else
k=next[k];//k去找前缀的末尾
}
}
//next是P和自己匹配
//KMP是P与S匹配
int KMP(char *S,char *P){
int n=strlen(S), m=strlen(P);
int next[N], i=0, j=0;
buildNext(P, next);
while(j<m && i<n){
if(j==-1||S[i]==P[j])
i++,j++;
else
j=next[j];
}
return i-j;
}最短路 bfs,Floyd,Dijkstra
无权连通图--bfs
//无权图 使用bfs;时间复杂度0(n+e)
void BFS(Vertex* Head,int n,int s,int dist[],int path[]){
queue<int> q;
for(int i=0;i<n;i++){
path[i]=-1;
dist[i]=-1;
}
dist[s]=0;
q.push(s);
while(!q.empty()){
int k=q.top();
q.pop();
for(Edge* p=Head[k].adjacent;p;p=p->link){
if(dist[p->veradj]==-1) {
dist[p->veradj]=dist[k]+1;
path[p->veradj]=k;
q.push(p->veradj);
}
}
}
}
//
void Dijkstra(Vertex *Head,int n,int s,int dist[],int path[]){
int S[N], i, j, min, v, w;
for(i=1; i<=n; i++) {path[i]=-1; dist[i]=INF; S[i]=0;}//初始化
dist[s]=0;
for(i=1; i<=n; i++) {
min=INF; //从不在S集合中的顶点中选D值最小的顶点v
for(j=1;j<=n;j++)
if(S[j]==0 && dist[j]<min){min=dist[j];v=j;}
S[v]=1; //将顶点v放入S集合;此时 s->v的最短路确定
for(Edge* p=Head[v].adjacent; p!=NULL; p=p->link) {
w=p->VerAdj; //更新v的邻接顶点的D值
if(S[w]==0 && dist[v]+p->cost<dist[w]) {
dist[w]=dist[v]+p->cost; path[w]=v;
}
}
}
}
void PrintPath(int path[], int s, int t){
//输出s到t的最短路
while(t!=s){
cout<<t<<" ";
t=path[t];
}
cout<<s;
}
//Floyd 用于无环负权图,求最短路
void Floyd(int A[N][N],int n,int D[N][N],int path[N][N]){
for(int i=1; i<=n; i++) //初始化
for(int j=1; j<=n; j++) {
D[i][j]=A[i][j];
if(i!=j && A[i][j]<INF) path[i][j]=j; //i和j间有边
else path[i][j]=-1;
}
for(int k=1; k<=n; k++) //递推构造Dn;n轮松弛
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++)
if(D[i][k]+D[k][j]<D[i][j]){
D[i][j]=D[i][k]+D[k][j];
path[i][j]=path[i][k];
}
}
void PrintPath1(int s, int t){
printf("%d ", s);
for(int k=s; k!=t; k=path[k][t])//path[k][t]表示从k走到t的路径的下一个结点
printf("%d ", path[k][t]);
} 最小支撑树,次小支撑树
最大支撑树:用Kruskal进行按降序sort;sort(E,n,greater<int>())
最小支撑树的最大边: 【动态规划】

// 两个最短路
//Prim 适合稠密图 0(n^2)
//Kruskal 适合稀疏图 0(eloge)
int maxcosts[N][N];
int Prim(intA[N][N],int n,int TE[]){//以点1为起点构造MST,返回权值和
//lowCost:到U集合的距离;
//U:是否已经在连通图内 -1;其他值:指向上一个顶点
int Lowcost[N],U[N],ans=0; //ans为mst边权之和
//初始化,1先入集合,与1相邻的边更新最短距离
for(int i=1;i<=n;i++)
{Lowcost[i]=A[1][i]; U[i]=1;}
U[1]=-1; //顶点1方入集合U
for(int i=1;i<n;i++){ //找n-1条边,循环n-1次
int v=0, min=INF; //找最小跨边
for(int j=1;j<=n;j++)
// 寻找未在U集合中的最短距离
if(U[j]!=-1 && Lowcost[j]<min){v=j; min=Lowcost[j];}
if(v==0) return INF; //不存在跨边,图不连通
//把v点加入MST中
TE[i].head=U[v];TE[i].tail=v;TE[i].cost=Lowcost[v];
maxcost[U[v]][v]= max(lowcost[v],maxcost[1][U[v]]);// 用于求次小支撑树
ans+=Lowcost[v]; U[v]=-1; //v加入U中,累加边权
for(int j=1;j<=n;j++)//更新v在V-U中的邻接顶点的Lowcost和U值
if(U[j]!= -1 && A[v][j]<Lowcost[j])
{ Lowcost[j]=A[v][j]; U[j]=v; }
}
return ans;
}
//并查集
int father[maxsize] = { 0 };
int Find(int x)
{
if (father[x] <= 0) return x;//按秩合并优化后,<=0的节点为父结点
return father[x] = Find(father[x]);//路径压缩;递归查找
}
void Union(int x, int y)
{
int fx = Find(x);
int fy = Find(y);
if (fx == fy) return;//如果祖先已经相同,无需合并
if (father[fx] < father[fy])
{
father[fy] = fx;//让秩较小的fy指向秩更大的fx
}
else
{
if (father[fx] == father[fy])
{
father[fy]--;//更新fy的秩,长度+1;
}
father[fx] = fy;
}
}
int Kruskal(Edge E[], int n, int e, Edge TE[]){
//E为图的边集数组,e为边数,n为顶点数,TE存mst的边集
for(int i=1;i<=n;i++) Make_set(i); //初始化
Sort(E,e); //对边按权值递增排序,时间复杂度O(eloge)
int ans=0,k=0; //ans为mst边权和,k为mst中边的计数器
for(int i=0;i<e;i++){ //从小到大依次扫描每条边
if(k==n-1) return ans;//边数=点数-1,找到了相应的最小支撑树
int u=E[i].head; int v= E[i].tail; int w=E[i].cost;
if(Find(u) != Find(v)){ //边(u,v)是最小生成树的一条边
TE[k].head=u; TE[k].tail=v; TE[k].cost=w;
k++; ans+=w; Union(u,v); //合并集合
}
}
return INF;
}
次小支撑树
用Prim()求出maxcost[][]和MST;遍历每条边,对不在MST中的、删去两点间最大边;加入该边获得一个可能的最小支撑树;
判断最小支撑树是否唯一,看MST和次小支撑树的权值是否相等 0(n^2)
int mintree[maxsize][maxsize] = { 0 }; //用邻接矩阵的方式存储最小生成树
int n = 5;
//用dfs找到形成的环中,除新加入的边 a-b 外,最长的一条边的权值
//即在原先的生成树中,从节点a到节点b的路径上最长的一条边的权值
void dfs(int v, int b, int visited[], int curw, int* maxw)
//curw是从节点a到当前节点v的路径上最长的一条边的权值
{
visited[v] = 1;
if (v == b) //如果找到了b节点
{
// 只有在遇到终点b时才能确定max的值就是a到b的路径上最大的边的权值
*maxw = curw;
return;
}
for (int i = 1; i <= n; i++)
{
if (mintree[v][i] != 0 && !visited[i])
{
int temp = curw; //记录一下原先curw的值,用于回溯
if (mintree[v][i] > curw) curw = mintree[v][i];
dfs(i, b, visited, curw, maxw);
curw = temp; //回溯
}
}
}
//向图中加入一条新边后,求最小生成树
void Add_newedge(int newa, int newb, int neww, int ans)
{
int visited[maxsize] = { 0 };
int maxw; //存储最长边的权值
dfs(newa, newb, visited, 0, &maxw);
printf("在原先的最小生成树中,节点%d到节点%d的路径上的最长边的权值为:%d\n\n", newa, newb, maxw);
if (neww < maxw)
//如果新加入的这条边的权值小于最长边的权值,那么就能够用这题新边代替原来的最长边
{
ans = ans - maxw + neww;
}
printf("加入边 %d--%d 后,新的最小生成树的权值为:%d\n",newa, newb, ans);
}
连通分量、强连通分量
//连通分量的数量
//非连通图调用多次dfs算法,一次dfs遍历一个连通分量
void DFS(Vertex* Head, int v, int vis[]){
//以v为起点进行深度优先搜索,vis初值为0
printf(“%d ”,v);
vis[v]=1;//访问顶点v
for(Edge* p=Head[v].adjacent;p!=NULL;p=p->link)//通过p循环扫描v的所有邻接顶点
If(vis[p->VerAdj]==0) //考察v的邻接顶点p
DFS(Head,p->VerAdj,vis);
}
for(int i=g;i<n;i++) //数组初始化
vis[0] = 0;
//以每个顶点为起点,试探是否能深搜
for(int i=0;i<n;i++)
if(vis[i]==0) DFS(Head,i,vis);
----------------------------------------------------
//只关注是否连通 传递闭包;时间复杂度0(n^3)
//注意区别并查集
void Warshall(int A[N][N], int n, int R[N][N]) {
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
if (i==j || A[i][j]<INF) R[i][j] = 1;
//i和j之间存在边,注意对无权图是A[i][j]==1
else R[i][j] = 0;
//类似无权图的Floyd的松弛操作
for (int k = 1; k <= n; k++) //递推构造Rn
for (int i = 1; i <= n; i++)
if(R[i][k] )// 优化
for (int j = 1; j <= n; j++)
if(R[k][j]) R[i][j]=1;
}
int SCC(int A[N][N],int n, int scc[]){//返回强连通分量个数
int R[N][N]={{0}}, vis[N]={0};
for(int i=1; i<=n; i++) scc[i]=0;
Warshall(A, n, R);// 0
int t=0; //t为强连通分量的编号
for(int i=1; i<=n; i++) //求顶点i所在的强连通分量
if(vis[i]==0){ //顶点i还没被放入某个强连通分量里,它可以自成一个连通分量
t++; vis[i]=1; scc[i]=t; //将顶点i放入强连通分量t
for(int j=i+1; j<=n; j++)//与i相互可及的点放入强连通分量t
if(j!=i && vis[j]==0 && R[i][j]==1 && R[j][i]==1){//强连通,i能到j且j能到i
vis[j]=1; scc[j]=t; //顶点j放入强连通分量t里 } }
return t;
}
二叉树逐层遍历
//二叉树的层次遍历;每层遍历结束的时候,入队NULL
//每层遍历时分情况讨论:如果NULL出队,表明当层遍历结束;再压入一个NULL来分层
//其他情况 :对叶子结点计数,把子结点压入栈
void LeafInEachLevel (Node *root){
if(root==NULL) return;
Queue q ;
int level=0, cnt=0;
q.ENQUEUE(root); q.ENQUEUE(NULL); //根和NULL入队
while (!q.IsEmpty()){
Node* p=q.DEQUEUE(); //出队一个结点
if(p==NULL) { //本层结束,输出叶结点数
printf("第%d层包含%d个叶结点。\n",level,cnt);
level++; cnt=0;
if(!q.IsEmpty()) q.ENQUEUE(NULL);
}
else{
if(p->left==NULL && p->right==NULL) cnt++;
if(p->left!=NULL) q.ENQUEUE(p->left);
if(p->right!=NULL) q.ENQUEUE(p->right);
}
}
};
//另一种:按照每层结点数,分层遍历
vector<vector<int>> levelOrder(TreeNode *root)
{
vector<vector<int>> ret;
if (!root)
return ret;
queue<TreeNode *> q;
q.push(root);
while (!q.empty())
{
int currNodeSize = q.size();
ret.push_back(vector<int>());
for (int i = 1; i <= currNodeSize; i++)
{
TreeNode *node = q.front();
q.pop();
ret.back().push_back(node->val);
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
return ret;
}
Stl
sort(nums.begin(), nums.end(), greater<int>());
//打印降序排序后的数组
//令nums数组中的元素升序排序
sort(nums.begin(), nums.end());
//赋值
v3.assign(v1.begin()+2, v1.end());
//第一个数据是起始地址,第二个数据是结束地址(不包括),第二个数据就是你要截取的长度加1
vector<int> a(b.begin(), b.begin()+3);
a.back(); //返回a的最后一个元素
a.front(); //返回a的第一个元素
5、clear() 函数
a.clear(); //清空a中的元素
a.empty(); //判断向量a是否为空,若为空空则返回true,非空则返回false
//---------------------------------------
set<K> a; //K为数据类型,如int, float等
a.count(A); //查找A是否存在, 存在返回1,不存在返回0
a.find(A); //如查找到返回迭代器,指向元素,不存在则返回 a.end()
a.insert(A); //向set中插入元素A
a.erase(A); //从set中擦出元素A
begin() ,返回set容器的第一个元素
end() ,返回set容器的最后一个元素
clear() ,删除set容器中的所有的元素
empty() ,判断set容器是否为空
size() ,返回当前set容器中的元素个数
//---------------------------------------
解忧
1
O(n);
int height[n]={0};//记录每个结点的深度
int parent[maxn];// 初始化 parent[0]=-1;
int nnode;//结点数量;
int ans=0;//记录树的高度;
int height[maxn];//记录已经求得的深度值,避免重复计算
//将height数组初始化为0,表示尚未计算深度。使用递归计算每一个结点的深度,逐次遍历:当某个节点的父亲结点的深度仍未计算时,先去计算其父结点的深度,该结点深度即为父结点深度+1,同时若该结点深度已经计算,则跳出深度计算,避免重复计算。将每次求得的深度与ans比较,使ans更新为最大值。
void solve(int n){
if(parent[n]==-1) {
height[n]=1;
return ;
}
else if(!height[parent[n]]) {
solve(parent[n]);
}
height[n]=height[parent[n]]+1;
return ;
}
int find_height(){
if(nnode==0) return 0;//空树 直接返回层数为0;
for(int i=1;i<=nnode;i++)
if(!height[i]) {
solve(i);
if(height[i]>ans) ans=height[i];
}
return ans;
}
O(n^2)
struct node{
int v;//顶点编号
int d;//距离
node(){}//无参构造要写上
node (int ww,int vv):d(ww),v(vv){}
};
int dij(int s,int w){
priority_queue<node> q;
for(i=1; i<=n; i++) {len[i]=0; dist[i]=INF; S[i]=0;}//初始化
//把起始点压入优先队列
dis[s]=0;
q.push(node(dis[s],s));
while(!q.empty()){
node tmp;
tmp=q.top();//使队列中的最短边出队列
q.pop();
int u=tmp.v;//u是最短的
S[u]=1;
for(Edge* p=Head[u].adjacent; p!=NULL; p=p->link) {
d=p->VerAdj;
if(S[d]==0 && dist[u]+p->cost<dist[d]) {
dist[d]=dist[u]+p->cost;
len[d]=len[u]+1;
q.push(node(dis[d],d));
}
else if(S[d]==1 &&dist[u]+p->cost==dist[d]&& len[d]>len[u]+1) {
len[d]=len[u]+1;
}
}
}
return len[w];
}
2.1

struct node{
int value;
node* next;
};
node* getI(int i,node* head){
if(i<=1) return NULL;
int d=1;
while(head!=NULL){
if(d==i) return head;//下标匹配 返回该结点
d++;
head=head->next;
}
return NULL;
//遍历整个链表,说明下标越界 返回NULL
}
struct node{
int val;
node* lr;
node* rr;
};
void num(node* root,int& count){
if(root==NULL) return ;
if(root->lr==NULL &&root->rr==NULL ) {
count+=1;
return ;
}
num(root->lr,count);
num(root->rr,count);
return ;
}
int num(node* root,int& count){
if(root==NULL) return ;
if(root->lr==NULL &&root->rr==NULL ) return 1;
return num(root->lr,count)+num(root->rr,count);
}
void find_path(node* root,vector<int>& curpath,vector<int>& res){
if(root==NULL) return;
curpath.push_back(root->val);
if(root->lr==NULL&& root->rr==NULL){
if(curpath.size()>res.size()) res=curpath; //更新
}
find_path(root->lr , curpath, res);
find_path(root->rr , curpath, res);
curpath.pop_back();
return ;
}
void finL(node* root){
vector<int> v1,v2;
v1.clear();
v2.clear();
find_path(root, v1, v2);
for(int i=0;i<v2.size();i++)
cout<<v2[i]<<" ";
}
#include<stdio.h>
#include<stack>
#include <iostream>
#define maxn 20001//定义最大顶点数
using namespace std;
int flag[maxn]={0};
bool visited[maxn]={0};
//边结点
struct ArcNode{
int adjvex;//该边所指向的顶点的位置
int w;
struct ArcNode *nextarc; //下一条边的指针
ArcNode(int x,int val):adjvex(x),w(val),nextarc(nullptr){}
};
// 顶点结点
struct VNode{
ArcNode* firstarc; //指向第一条依附该顶点的边的指针
} ;
//定义邻接表的结构
struct ALGraph{
VNode vertices[maxn];
int vexnum, arcnum; //顶点数和边数
};
//一个无向图是一棵树的条件是:G必须是无回路的连通图或者有n-1条边的连通图。
/本算法中采用深度优先搜索算法在遍历图的过程中统计可能访问到的顶点个数和边的条数。若一次就遍历访问到N个顶点和n-1条边。则为一棵树。
void DFS(ALGraph &G,int v,int &vNum,int &eNum,bool visited[]){
visited[v]=true;
vNum++;
ArcNode* p=G.vertices[v].firstarc;
for(;p!=NULL;p=p->nextarc){//当邻接顶点存在
eNum++;//边存在,边计数
if(!visited[p->adjvex]){//当前结点未访问过,无向图一条边会出现两次,避免重复
DFS(G,p->adjvex,vNum,eNum,visited);
}
}
}
bool isTree(ALGraph &G){
for(int i=1;i<=G.vexnum;i++) visited[i]=false;
int vNum=0,eNum=0;
DFS(G,1,vNum,eNum,visited);
cout<<vNum<<" "<<eNum<<endl;
if(vNum == G.vexnum && eNum == 2*(G.vexnum-1))
// 一次深度搜索 找到 n-1条边,n个点;则是树
return true;
else
return false;
}3.1

//以K为基准元素,使用快速排序的一次分划
int A[maxn] ;
int K;
int n;
void Sort(){
int i=1;
int j=n;
while(i<j){
while(i<=n&&A[i]<K) i++;
while(j>-1&&A[j]>K) j--;
if(i<j) swap(A[i],A[j]);
}
return ;
}
4
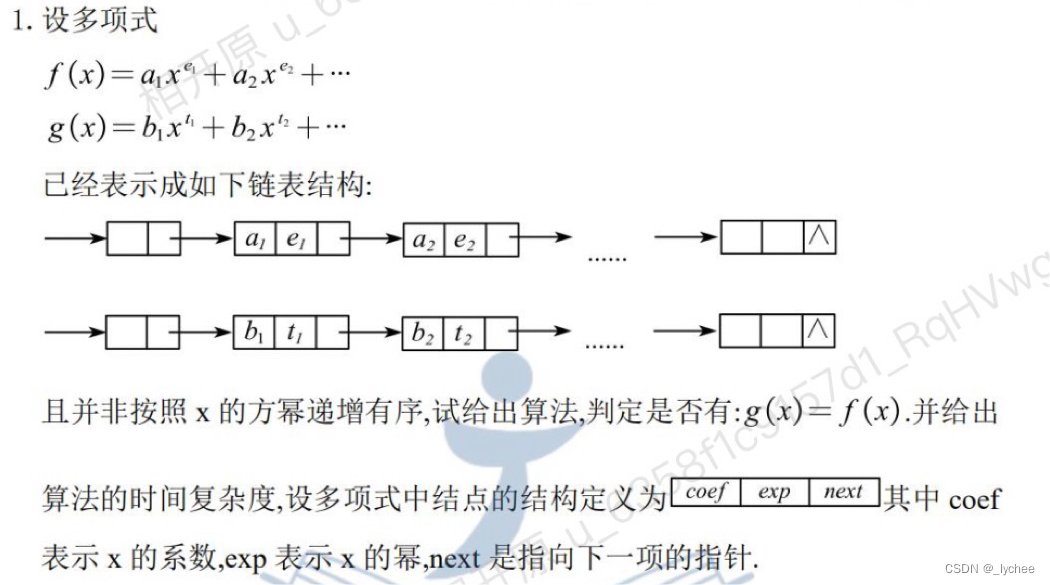
struct node{
int coef;//系数
int exp;//指数
node* next;
};
//nlogn
bool is_equal(node *f,node* g){
map<int,int> m;
node* p=f->next;// head是哨兵结点
while(p){
if(m.find(p->exp)==m.end()){//第一次出现该指数
m.insert(make_pair(p->exp,p->coef));
}
else m[p->exp]+=p->coef;//第二次出现,做加法
p=p->next;
}
p=g->next;
while(p){
if(m.find(p->exp)==m.end()){
return false;//g中出现了f未出现的结点
}
else m[p->exp]-=p->coef;
p=p->next;
}
for(auto it=m.begin();it!=m.end();it++){
if(it->second!=0) return false;
}
return true;
}
struct Edge{
int Veradj ;
Edge* link;
};
struct Vertex{
int Vername ;
Edge* adjvex;
}* list[Maxn];
int D[Maxn]={0};//用数组记录入度, 0(n+e)
void In_degree(Vertex* list[],int n, int D[]){
for(int i=1;i<=n;i++) D[i]=0;
for(int i =1;i<=n;i++){
for(Edge* p=list[i]->adjvex; p;p=p->link){
D[p->Veradj]++;
}
}
}
struct node{
int key;
node* left;
node* right;
};
node* find(node *tree){
//走最右边的路
node* p=tree;
while(p){
if(p->right) p=p->right;
else if(p->left) p=p->left;//当右根走到底,再走左边
else break;
}
return p;
}
void Del(node* tree){
if(tree==NULL) return ;
Del(tree->left);
Del(tree->right);
delete tree;
}
void delete_key(int x ,note* tree ,node* pre){//pre初始化 tree->left
if(tree==NULL) return ;
node* p=tree;
if(p->key<x) {
pre=tree;
delete_key(x ,tree->right);//只有右子树需要删除
}
else{
node* p=tree->left;
Del(tree->right);//删除右子树的所有结点
delete tree;//删除根结点
pre->right=p;//让父结点的右子树指向tree的左子树
delete_key(x, p, pre);//对左子树继续继续删除
}
}5
struct node{
int val;
node* next;
};
node* combine(node* f, node*g){
node* newn =new node ;
node* p;
f=f->next;
g=g->next;//假设有哨兵结点
while(f&&g){//f\g都不为空
if(f->val<g->val){ //选择较小的插入
p=f;
f=f->next;
}
else {
p=g;
g=g->next;
}
p->next=newn;
newn=p;
}
while(f){//g为0,f不为0;把剩下的f用头插法插入
p=f;
f=f->next;
p->next=newn;
newn=p;
}
while(g){//
p=g;
f=g->next;
p->next=newn;
newn=p;
}
return newn;
}
struct node{
int data;
node *left;
node* right;
};
int count=0;
//dfs
void count_leaf(node* tree, int &ans ,int height ){
if(tree==NULL ||height>k) return ans;
if(height==k && tree->left==NULL && tree->right==NULL){
ans++;
return ;
}
count_leaf(tree->left,ans, height+1);
count_leaf(tree->right ,ans, height+1);
return ;
}
count(tree, count, 0);
//层次遍历
int levelOrder(TreeNode *root,int k)
{
int ans=0;
int lever=0;
if (!root)
return 0;
queue<TreeNode *> q;
q.push(root);
while (!q.empty())
{
int currNodeSize = q.size();//获得单层的元素个数
lever++;
if(lever>k) return ;
//单层遍历
for (int i = 1; i <= currNodeSize; i++)
{
TreeNode *node = q.front();
q.pop();
if(ans==k&& node->left==NULL &&node->right ==NULL ){
ans++;
}
if (node->left)
q.push(node->left);
if (node->right)
q.push(node->right);
}
}
return ans;//返回第k层元素个数
}
6
1.颠倒链表的链接
struct node{
int val;
node* next;
};
node Reverse(node * head){
if(head==NULL||head->next==NULL) return ;//只有0/1个元素,直接返回
node* pre,*p,*next_node;
pre=NULL;// 指向已经翻转的nodelist的首结点;
p=head->next// 指向即将要翻转的结点
next_node=NULL// 指向要翻转的结点的下一个结点
while(p2!=NULL){
next_node=p->next;//记录
p->next=pre;//翻转
pre=p;//更新头结点;
p=next_node;//更新下一个翻转的结点;
}
return pre;
}2.对以左儿子、右兄弟链接表示的树,编写树的深度的算法

struct node{
int val;
node* firstchild;
node* nextbrother;
};
int height(node* head){
return head==NULL?-1:max(height(head->firstchild)+1,height(head->nextbrother));
}

简单路径:其顶点序列中不含有重现的顶点
struct Edge{ //边结点的结构
int VerAdj; //邻接顶点序号
int cost; //边的权值
Edge *link; //指向下一个边结点的指针
};
struct Vertex{ //顶点表中结点的结构
int VerName; //顶点名称
Edge *adjacent;//边链表的头指针
} *List[maxn];
int visited[maxn];
bool check(int i,int j,int k){
//递归出口
if(i==j&& k==0) return true;//走到啦
if(k<0) return false;//剪枝
//k>0 继续递归
visited[i]=1;//满足简单路径的要求,一条路径不能有重复顶点
for(Edge* p = List[i]->adjacent;p!=NULL;p=p->link){
if(!visited[p->VerAdj] ) {
if(check(p->VerAdj,j,k-p->cost)) return true;
}
if( i==j && j==p->Veradj && (k- p->cost )==0) return true;//简单回路
visited[i]=0;
}
return false;
}7

void Quicksort (int D[],int n){
int i=0,j=n-1;
while(i<j){
while(D[i]<0){
i++;
}
while(D[j]>0&&i<j){
j--;
}
int temp=D[i];
D[i]=D[j];
D[j]=temp;
}
}
struct Edge*{
int veradj;
node* link;
Edge(int x, node* l ):veradj(x),link(l){}
};
struct Vertex{
int Vername;
Edge* adjacent;
};
//图的逆邻接表反映的是节点的入度邻接情况
void Tranverse(Vertex *fir[],int n){
Vertex* ver_in[N];
for(int i=0;i<n;i++){
ver_in[i].Vername=i;
ver_in[i].adjacent=NULL;
}
for(int i=0;i<n;i++){
Vertex* ver=fir[i];
for(Edge* p=ver->adjacent; p ;p=p->link){
Edge* newn=new Edge(ver.Vername, ver_in[p->veradj]->adjacent);//头插法
ver_in[p->veradj].adjacent=newn;//更新邻接表头;
}
}
}

#include <iostream>
#include <vector>
using namespace std;
//测试数据 :2 3 5 0 0 6 8 0 0 0 4 7 0 0 0
struct node{
int val;
node* left;
node* right;
node(int x):val(x),left(NULL),right(NULL){}
};
void Create_tree(node*& t){
int x;
cin>> x;
if(x==0) t=NULL;
else {
node* p=new node(x);
t=p;
Create_tree(t->left);
Create_tree(t->right);
}
}
//找从根节点到叶子结点的最长路径,采用深度搜索,记录当前路径和最长路径;当访问到叶子结点时,将当前路径长度和最长路径长度比较,更新最长路径;
void search_p(vector<vector<int>> &path, node* tree,vector<int> &lpath ,vector<int> &cur){
if(tree==NULL ) return ;
cur.push_back(tree->val);
if(tree->left==NULL&& tree->right==NULL) {// 叶子结点
path.push_back(cur);
if(cur.size()> lpath.size()) lpath=cur;
cur.pop_back();
return ;
}
search_p(path,tree->left,lpath,cur);
search_p(path,tree->right,lpath,cur);
cur.pop_back();
}
int main(){
node* tree;
Create_tree(tree);
vector<vector<int>> path;
vector<int> lpath;
vector<int> cur;
search_p( path, tree, lpath, cur);
for(int i=0;i<path.size();i++){
for(int j=0;j<path[i].size();j++) cout<<path[i][j]<<" ";
cout<<endl;
}
for(int j=0;j<lpath.size();j++) cout<< lpath[j]<<" ";
}
**
#include<bits/stdc++.h>
using namespace std;
void BinarySearch(int R[],int n, int K,int& cnt){
//在R中对半查找K,R中关键词递增有序
int s = 0, e = n, mid;
while(s <= e){
mid=(s+e)/2; //若有整型溢出风险,可令mid=s+(e-s)/2
if( (K>R[mid] && K<R[mid+1] )|| (mid==n&& K>R[mid])) {
cnt=mid+1;
return ;
}
else if(K<R[mid]) e=mid-1; //在左半部分查找
else s=mid+1; //K>R[mid],在右半部分查找
}
return ;
}
int Partition(int R[], int m, int n){ //对子数组R m-n进行分划
int mid=(m+n)/2;
//把三者中最大的移到R[n]的位置
if(R[mid]>R[n]) swap(R[mid],R[n]);
if(R[m]>R[n]) swap(R[m],R[n]);
//在m和mid中选一个更大的作为基准元素
if(R[m]<R[mid]) swap(R[m],R[mid]);
//正常的分划
int i=m, j=n+1,K=R[m]; // Rm为基准元素
while(i<j) {
while(++i<=n && R[i]<=K); //从左向右找第一个>K的元素
while(R[--j]>K); //从右向左找第一个<K的元素
if(i<j) swap(R[i],R[j]);
} //不断把小于K的元素换到数组左边,大于K的元素换到数组右边,直至指针i和j相遇
swap(R[m],R[j]);
return j; // <K 的元素在j左边,>k的元素在j右边
}
void QuickSort(int R[], int m, int n){ //对Rm…Rn递增排序
if(m < n){
int j=Partition(R, m, n);
QuickSort(R, m, j-1);
QuickSort(R, j+1, n);
}
}
int main(){
int A[]={3,24,35,20,12};
int B[]={2,36,56,15,4};
int C[7]={0};
int n=5;;
QuickSort(B,0,n-1);
for(int i=0;i<n;i++)
cout<<B[i]<<endl;
for(int i=0;i<n;i++) {
BinarySearch(B, n, A[i],C[i]);
cout<<C[i];
}
}
//很经典的使用双指针法
struct node{
int data;
node* link;
};
//时间复杂度 0(n)
int locate(int k, node* head){
node* p1=head->link,*p2=head->link;
while(k--&& !p1){
p1=p1->link;
}
if(k) return 0;//单链表的长度小于k;
while(p1){
p2=p2->link;
p1=p1->link;
}
printf("%d",p2->val);
return 1;
} 
要求遍历一遍二叉树的同时记录从根结点到某一结点的路径
【考试一定要详细写的思想,多写点废话 】:对树进行先根遍历,在遍历到树的某一点时把该数据压栈,然后去访问其左右孩子结点,访问结束后再将该数据出栈。当找到p结点时,当前栈即为所求,所以直接返回,不进入下一步递归。
#include <iostream>
#include <vector>
#include<stack>
using namespace std;
//测试数据 :2 3 5 0 0 6 8 0 0 0 4 7 0 0 0
struct node{
int data;
node* left;
node* right;
node(int x):data(x),left(NULL),right(NULL){}
};
void Create_tree(node*& t){
int x;
cin>> x;
if(x==0) t=NULL;
else {
node* p=new node(x);
t=p;
Create_tree(t->left);
Create_tree(t->right);
}
}
void record_path(bool& flag, node* tree, stack<int>& s,int p){//flag初始为0
if(tree==NULL||flag) return;
s.push(tree->data);
if(tree->data==p){
flag=1;
return ;
}
record_path(flag, tree->left,s,p);
record_path(flag, tree->right,s,p);
if(!flag) s.pop();
}
int main(){
node* tree;
Create_tree(tree);
stack<int> s;
bool flag=0;
int p=7;
record_path(flag, tree, s, p);
while(!s.empty()){
int p=s.top();
s.pop();
cout<<p<<" ";
}
}9

struct Edge{
int veradj;
Edge* link;
Edge(int x):veradj(x),link(NULL){}
};
struct Vertex{
int vername ;
Edge* adjacent;
Vertex(int x):vername(x),adjacent(NULL){}
};
bool path_p( int u, int v,Vertex* Head[],bool& visit ){//visit 初始为0,标记u点是否能被访问
if(visit ) return true;//已经访问到u
for(Edge* p=Head[v]->adjacent;p;p=p->link){//从v的邻边出发递归遍历
if(p->veradj==u ) {
visit=true;
}
if(!visit) path_p(u ,p->veradj, Head,visit);//如果未访问到u继续遍历直至穷尽
else break;
}
return visit;
}**

->空树:返回true
->树不为空:将根节点入队列,设置isLeafOrLeft=false(表示没有找到第一个不饱和节点),循环执行如下操作(循环条件:队列不为空):
将队头元素出队列并标记:cur=queue.poll();
找到第一个不饱和节点:
从第一个不饱和结点之后,所有节点不能有孩子,如果有左孩子或者右孩子:返回false
没有找到第一个不饱和节点,继续按照层序遍历寻找:
-cur节点(当前节点)左右孩子都存在:左孩子入队列,右孩子入队列
-cur只有左孩子:即找到第一个不饱和节点,标记isLeafOrLeft=true
-cur只有右孩子:找到不饱和节点,一定不是完全二叉树,返回false
-cur是叶子节点:找到不饱和节点:标记isLeafOrLeft=true
详见:https://blog.csdn.net/yuiop123455/article/details/109542938























 3715
3715











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








