生活用纸抗张强度预测Baseline

★★★ 本文源自AI Studio社区精品项目，【点击此处】查看更多精品内容 >>>

---

直接一键全部运行即可

大赛背景

在产业中，造纸、建材、食品等流程工业是具有上百年发展史的行业，是关乎国计民生的基础材料制造业。近20年来人工智能技术正高速发展，以智能化为核心的产业变革不断蔓延，工艺AI技术逐步成为推动流程工业数智化、绿色化转型升级的关键燃料。
本次大赛基于流程工业当下面临的人力资源、原料品质、碳排放等一系列时代挑战，为大时代青年们提供一个实现产业抱负的舞台，从最前沿的行业需求及痛点出发，通过大数据、人工智能等技术，结合工业实际场景设计算法解决方案和研发AI模型，参与行业革新，驱动产业变革。

赛题介绍

赛题名称

生活用纸抗张强度预测

赛题背景

造纸术作为我国的四大发明之一， 在推动人类文明的发展上起到了重大的作用，历经千年发展，纸的用途基本已经覆盖了各行各业，在人们日常生活中扮演着不可替代的角色。
生活用纸是日常生活中最常见的纸，该纸种主要供人们日常卫生之用。据统计，全球每年的生活用纸用量达到了4400万吨，我国每年的生活用纸量超过1000万吨。
本次赛题的研究对象是生活用纸的质量问题，目前，生活用纸企业的纸张质量检测主要是通过人工抽检样品进行仪器检查，这种质检方式存在质检覆盖率低、操作成本高且时间滞后度大的问题，由此可能导致不合格产品漏检和误判进而造成直接的经济损失。因此，实现生活用纸质量指标的实时软测量，对提升生活用纸行业产品质量的价值是巨大的。

赛题任务

本次赛题的研究对象是生活用纸的质量问题。抗张强度是生活用纸质量的一个重要指标（表征纸张在一定条件所能承受的最大张力），赛题的任务即完成该质量指标的预测，我们期望参加比赛的选手能深入理解造纸的业务流程，结合主办方提供的工艺数据，建立一个能准确量化评估抗张强度的模型。

数据简介

为了进行生活用纸抗张强度建模，主办方提供的数据主要包括具体质量指标的检测结果、关键过程检测数据和纸机运行参数数据。

竞赛网站：https://www.datafountain.cn/competitions/614

Baseline方案

基于PaddleSlim的GPNAS构建回归器预测抗张强度，方案得分0.906

• 赛题任务可建模为一个回归任务，输入数据为纸张的检测数据和工序运行实时参数，通过对数据进行特征提取回归出纸张的抗张强度系数。

• 基线模型选择了目前正在学习的GPNAS。PaddleSlim组件中的GPNAS针对NAS（网络结构搜索）任务设计，该任务是对输入的网络结构来预测此结构的网络性能，NAS任务同为回归任务，因此GPNAS可以直接迁移到本赛题任务中，不需要过多的修改。

• GPNAS是基于高斯过程的回归算法，从贝叶斯的角度对数据相关性进行建模。具体来说，通过介绍一种新颖的基于高斯过程的NAS (GP-NAS)方法，采用核函数和平均函数对相关性进行建模。内核函数也是可学习的，以实现复杂的自适应建模不同数据空间的相关性。此外，通过结合基于互信息的采样方法，GPNAS理论上只需要少量样本集

安装 PaddleSlim

!pip install paddleslim

引入依赖

import pandas as pd
import numpy as np

from paddleslim.nas import GPNAS 

训练数据处理

数据分析

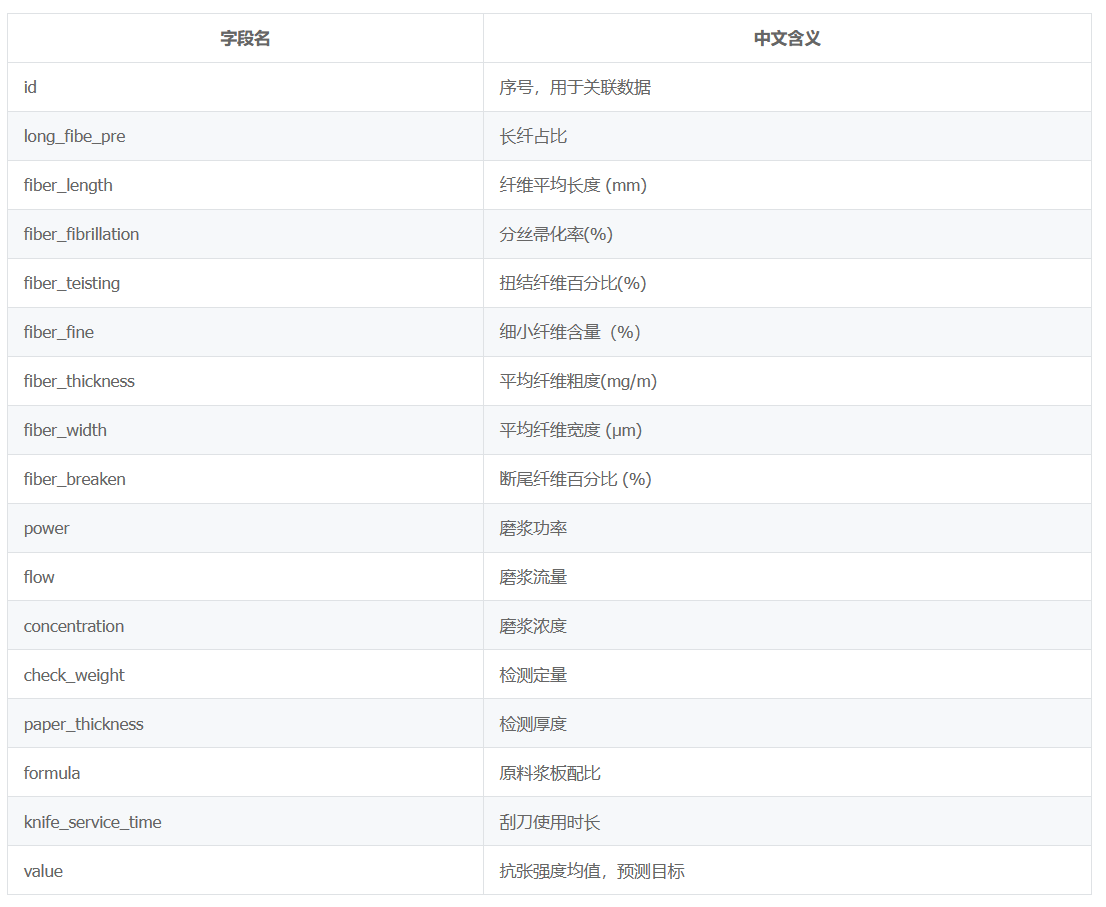
• 训练数据一共包含18维信息

• 从下面的结果能看到，各维度数据基本都是数值型，但formula为不同材料的配比，对formula数据进行数值编码

• 编码方式为统计所有的材料配比，共440种，因此将formula信息编码为0~439的int数值，和其他维度信息一同输入GPNAS进行训练

import pandas as pd
train = pd.read_csv('train.csv')

print(train.columns)
print('='*90)
print(train.head(2))
print('='*90)
print(train['formula'][0])

Index(['id', 'end_time', 'long_fibe_pre', 'fiber_length', 'fiber_fibrillation',
       'fiber_teisting', 'fiber_fine', 'fiber_thickness', 'fiber_width',
       'fiber_breaken', 'power', 'flow', 'concentration', 'check_weight',
       'paper_thickness', 'formula', 'knife_service_time',
       'paper_tension_vertically_average'],
      dtype='object')
==========================================================================================
   id             end_time  long_fibe_pre  fiber_length  fiber_fibrillation  \
0   0  2019-04-01 00:26:00       0.092284      0.155232            0.811812   
1   1  2019-04-01 05:01:00       0.092284      0.155232            0.811812   

   fiber_teisting  fiber_fine  fiber_thickness  fiber_width  fiber_breaken  \
0        0.272328    0.259538         0.240404     0.161614       0.147387   
1        0.272328    0.259538         0.240404     0.161614       0.147387   

      power      flow  concentration  check_weight  paper_thickness  \
0  0.461538  0.133333       0.333333      0.355967         0.237410   
1  0.461538  0.133333       0.333333      0.336763         0.249509   

                                       formula  knife_service_time  \
0  （0.5件芬宝)：（2件森博+2件绿桉+1件鹦鹉+1件明星）=7.69%：92.31%            0.007543   
1  （0.5件芬宝)：（2件绿桉+2件森博+1件明星+1件鹦鹉）=7.69%：92.31%            0.008146   

   paper_tension_vertically_average  
0                            1067.0  
1                             980.0  
==========================================================================================
（0.5件芬宝)：（2件森博+2件绿桉+1件鹦鹉+1件明星）=7.69%：92.31%

件绿桉+1件鹦鹉+1件明星）=7.69%：92.31%

代码实现

• formula编码方式为统计所有的材料配比，共440种，因此将formula信息编码为0~439的int数值

• formula信息和其他维度信息拼接，作为GPNAS输入数据

train = pd.read_csv('train.csv')
test_A = pd.read_csv('test_A.csv')

data_list, label_list = [], []

formula_array = pd.concat([train['formula'], test_A['formula']]).unique()

for i in range(train.shape[0]):
    row = np.asarray(train.iloc[i])
    row[-3] = np.where(formula_array == row[-3])[0][0]
    row = list(row)
    data_list.append(row[2:-1])
    label_list.append(row[-1])

训练GPNAS预测器

• GP-NAS已经集成在PaddleSlim模型压缩工具中

• GP-NAS论文地址 https://openaccess.thecvf.com/content_CVPR_2020/papers/Li_GP-NAS_Gaussian_Process_Based_Neural_Architecture_Search_CVPR_2020_paper.pdf

train_num = 800

gp = GPNAS(2, 2)
# 划分训练及测试集
X_all, Y_all  = np.array(data_list), np.array(label_list)
X_train, Y_train, X_test, Y_test = X_all[0:train_num:1], Y_all[0:train_num:1], X_all[train_num::1], Y_all[train_num::1]
# 初始该任务的gpnas预测器参数
gp.get_initial_mean(X_train[0::2],Y_train[0::2])
init_cov = gp.get_initial_cov(X_train)
# 更新（训练）gpnas预测器超参数
gp.get_posterior_mean(X_train[1::2],Y_train[1::2])  

matrix([[ 7.63295468e+02],
        [ 7.80342250e+00],
        [ 1.38523831e+03],
        [ 2.63319838e+02],
        [-6.14061569e+01],
        [-2.97090214e+02],
        [-8.68600122e+01],
        [ 2.85169066e+02],
        [-2.68301117e+02],
        [ 3.92198423e+02],
        [-3.15672144e+01],
        [ 3.11616959e+03],
        [-4.02107629e+03],
        [ 5.11416072e-01],
        [ 9.71078375e+01],
        [-3.51079401e+02]])

测试数据处理

• 测试数据处理方式和训练数据相同

test_list = []

for i in range(test_A.shape[0]):
    row = np.asarray(test_A.iloc[i])
    row[-2] = np.where(formula_array == row[-2])[0][0]
    row = list(row)
    test_list.append(row[2:])

预测结果并提交

• 按照赛题要求，将预测结果保存为csv文件，下载后即可提交

X_test = np.array(test_list)

y_predict = gp.get_predict(X_test)

test_A['value'] = y_predict
result = test_A[['id', 'value']]
result.to_csv('submit.csv', index=False)