文章目录
一、质数
1.1、质数筛(筛1~n中的所有质数)
时间复杂度:O(n)
//N是要筛的质数范围,prime存储质数
#include<vector>
void Prime_sieve(int N,vector<int> & prime){
vector<int> notp(N+1);
notp[1]=1;//初始化为0,因此默认一个数是质数,不是质数用1标记
for(int i=2;i<N;++i){
if(!notp[i]) prime.push_back(i);
//如果一个数没被标记,其一定是质数,不是质数的一定被其最小质因数标记了。
for(int j=0;j<prime.size();++j){
if(i * prime[j]>N) break;//范围超限,之后都超限,直接不管了
notp[i*prime[j]]=1;//这个数一定不是质数
if(i % prime[j]==0) break;//prime[j]是i的最小质因数! 退出咯
}
}
return;
}
1.2、判断一个数是否为质数
时间复杂度:O(
(
n
)
\sqrt(n)
(n))
//num是需要判断是质数,函数返回为true则为质数
#include<cmath>
bool Is_prime(int num){
if(num==1) return false;
if(num==2||num==3) return true;
if(num%6!=1&&num%6!=5) return false;
if(num%2==0||num%3==0) return false;
int j=sqrt(num);
for(int i=5;i<=j;i+=6){
if(num%i==0||num%(i+2)==0){
return false;
}
}
return true;
}
1.3、对一个数进行质因数分解
时间复杂度:O(
(
n
)
\sqrt(n)
(n))
//N是要进行分解的数,factor存储分解结果,nums存每个质因数的次数
#include<vector>
void prime_factorization(int N,vector<int> & factor,vector<int> & nums){
for(int i=2;i*i<=N;++i){
if(N%i==0){
factor.push_back(i);
nums.push_back(0);
while(N%i==0) {nums[nums.size()-1]++;N/=i;}
}
}
if(N>1) {factor.push_back(N);nums.push_back(1);}
return;
}
二、快速幂
2.1、费马小定理——乘法逆元
时间复杂度:O(
(
p
)
\sqrt(p)
(p))
//n^(p-1)≡1 (mod p) n的乘法逆元是n^(p-2)
long long inverse_element(long long n,long long p){
long long x=1;
long long p=1e9+7;
long long b=p-2;
while(b){
if(b&1) x=(x*n)%p;
n=(n*n)%p;
b>>=1;
}
return x;//x是n的乘法逆元
}
2.2、快速幂
时间复杂度:O(
(
n
)
\sqrt(n)
(n))
//求n^b,答案是x
#include <limits>
long long fast_pow(long long n,long long b){
long long x=1;
long long p=std::numeric_limits<long long>::max();
while(b){
if(b&1) x=(x*n)%p;
n=(n*n)%p;
b>>=1;
}
return x;
}
三、约数
3.1、N个数的正约数集合
时间复杂度:O(NlogN)
//求1~N所有数的正约数集合
#include<vector>
void N_Set_of_positive_divisors(int N,vector<vector<int> >& factor){
factor.assign(N,vector<int>{});
for(int d=1;d<=N;++d)
for(int i=1;i<=N/d;++i){
factor[d*i].push_back(d);
}
return;
}
3.2、一个数的正约数集合
时间复杂度:O(
(
n
)
\sqrt(n)
(n))
#include<cmath>
#include<vector>
void Set_of_positive_divisors(int num,vector<int> & factor){
float j=sqrt(num);
for(int i=1;i<j;++i){
if(num%i==0){//我们限制i在根号N的取地板之下,必然保证了成对出现
factor.push_back(i);
factor.push_back(num/i);
}
}
if(int(j)*int(j)==num) factor.push_back(j);
return 0;
}
四、欧拉函数(互质数数目)
时间复杂度:O(
(
n
)
\sqrt(n)
(n))
//求n的欧拉函数
int Set_of_prime(int n){
int ans=n;
for(int i=2;i*i<=n;++i){
if(n%i==0){
ans=ans/i*(i-1);
while(n%i==0){
n/=i;
}
}
}
if(n>1) ans=ans/n*(n-1);
return ans;
}
五、最大公约数
5.1、__gcd(a,b)
时间复杂度:O(log min(a, b))
//c++,GCC提供的一个非标准扩展,因此在非GNU编译器中可能不可用。
#include<algorithm>
int gcd(int a, int b){
return __gdc(a,b);
}
5.2、欧几里得算法
时间复杂度:O(log min(a, b))
int gcd(int a, int b){
return b ? gcd(b, a % b) : a;
}
5.3、扩展欧几里得
它不仅能计算出两个整数a和b的最大公约数,还能找到整数x和y(其中x和y可能为正数或负数),使得它们满足贝祖等式
[ ax + by = gcd(a, b) ]
// 求x, y,使得ax + by = gcd(a, b),并返回gcd(a,b) 这里是d
int exgcd(int a, int b, int &x, int &y)
{
if (!b)
{
x = 1; y = 0;
return a;
}
int d = exgcd(b, a % b, y, x);
y -= (a/b) * x;
return d;
}
以下借鉴:常用代码模板4
六、组合数
6.1、递推法求组合数(可以求出以0~n为底的所有组合数)
时间复杂度:O(
n
2
n^{2}
n2)
// c[n][m] 表示从n个苹果中选m个的方案数
for (int i = 0; i < N; i ++ )
for (int j = 0; j <= i; j ++ )
if (!j) c[i][j] = 1;
else c[i][j] = (c[i - 1][j] + c[i - 1][j - 1]) % mod;
6.2、通过预处理逆元的方式求组合数(C(n,k)%p)
预处理时间复杂度:O(n)
每次组合数求解时间复杂度:O(1)
int qmi(int a, int k, int p) // 快速幂模板
{
int res = 1;
while (k)
{
if (k & 1) res = (LL)res * a % p;
a = (LL)a * a % p;
k >>= 1;
}
return res;
}
// 预处理阶乘的余数和阶乘逆元的余数
vector<int> fact(max_len,0);
vector<int> infact(max_len,0);
fact[0] = infact[0] = 1;
for (int i = 1; i < N; i ++ )
{
fact[i] = (LL)fact[i - 1] * i % mod;
infact[i] = (LL)infact[i - 1] * qmi(i, mod - 2, mod) % mod;
}
//实际组合数 只需调用如下函数求 C(n,k)%p
int C(int n, int k, int p) {
if (k > n) return 0;
return (LL)fact[n] * infact[k] % p * infact[n - k] % p;
}
七、卡特兰数
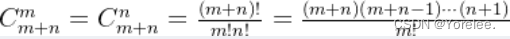
八、第二类斯特林数
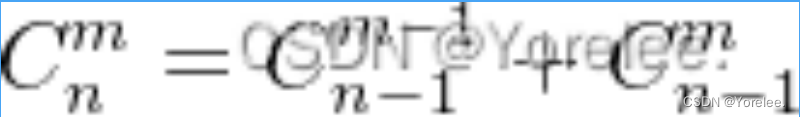


























 78
78











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










