几种常见的排序算法

1.时间复杂度O(n^2)级排序算法

A 冒泡排序

冒泡排序是入门级的算法，但也有一些有趣的玩法。通常来说，冒泡排序有三种写法：

• 一边比较一边向后两两交换，将最大值 / 最小值冒泡到最后一位；
• 经过优化的写法：使用一个变量记录当前轮次的比较是否发生过交换，如果没有发生交换表示已经有序，不再继续排序；
• 进一步优化的写法：除了使用变量记录当前轮次是否发生交换外，再使用一个变量记录上次发生交换的位置，下一轮排序时到达上次交换的位置就停止比较。

冒泡排序的第一种写法

代码如下：

public static void bubbleSort(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        for (int j = 0; j < arr.length - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                // 如果左边的数大于右边的数，则交换，保证右边的数字最大
                swap(arr, j, j + 1);
            }
        }
    }
}
// 交换元素
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

最外层的 for 循环每经过一轮，剩余数字中的最大值就会被移动到当前轮次的最后一位，中途也会有一些相邻的数字经过交换变得有序。总共比较次数是(n−1)+(n−2)+(n−3)+…+1。

这种写法相当于相邻的数字两两比较，并且规定：“谁大谁站右边”。经过n−1轮，数字就从小到大排序完成了。整个过程看起来就像一个个气泡不断上浮，这也是“冒泡排序法”名字的由来。

冒泡排序的第二种写法

第二种写法是在第一种写法的基础上改良而来的：

public static void bubbleSort(int[] arr) {
    // 记录每轮冒泡是否发生了交换
    boolean swapped;
    for (int i = 0; i < arr.length - 1; i++) {
        swapped = false;
        for (int j = 0; j < arr.length - 1 - i; j++) {
            if (arr[j] > arr[j + 1]) {
                swap(arr, j, j + 1);
                swapped = true;
            }
        }
        // 如果没有发生过交换，直接退出循环
        if (!swapped) break;
    }
}

最外层的 for 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。这种写法相对于第一种写法的优点是：如果一轮比较中没有发生过交换，则立即停止排序，因为此时剩余数字一定已经有序了。

看下动图演示：

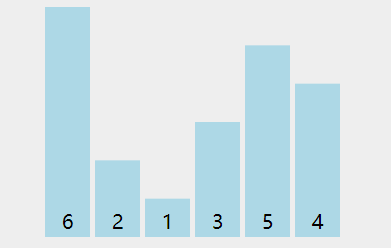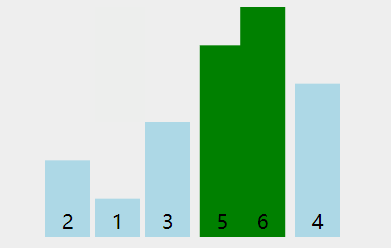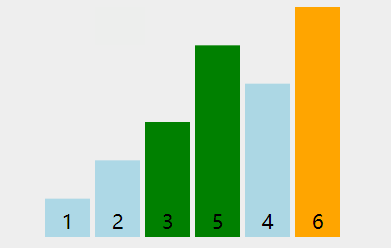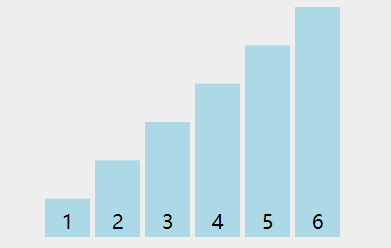
图中可以看出：

• 第一轮排序将数字 66 移动到最右边；
• 第二轮排序将数字 55 移动到最右边，同时中途将 11 和 22 排了序；
• 第三轮排序时，没有发生交换，表明排序已经完成，不再继续比较。

冒泡排序的第三种写法

第三种写法比较少见，它是在第二种写法的基础上进一步优化：

public static void bubbleSort(int[] arr) {
    boolean swapped = true;
    // 最后一个没有经过排序的元素的下标
    int indexOfLastUnsortedElement = arr.length - 1;
    // 上次发生交换的位置
    int swappedIndex = -1;
    while (swapped) {
        swapped = false;
        for (int i = 0; i < indexOfLastUnsortedElement; i++) {
            if (arr[i] > arr[i + 1]) {
                // 如果左边的数大于右边的数，则交换，保证右边的数字最大
                swap(arr, i, i + 1);
                // 表示发生了交换
                swapped = true;
                // 更新交换的位置
                swappedIndex = i;
            }
        }
        // 最后一个没有经过排序的元素的下标就是最后一次发生交换的位置
        indexOfLastUnsortedElement = swappedIndex;
    }
}
// 交换元素
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

经过再一次的优化，代码看起来就稍微有点复杂了。最外层的 while 循环每经过一轮，剩余数字中的最大值仍然是被移动到当前轮次的最后一位。

在下一轮比较时，只需比较到上一轮比较中，最后一次发生交换的位置即可。因为后面的所有元素都没有发生过交换，必然已经有序了。

当一轮比较中从头到尾都没有发生过交换，则表示整个列表已经有序，排序完成。

测试：

public void test() {
    int[] arr = new int[]{6, 2, 1, 3, 5, 4};
    bubbleSort(arr);
    // 输出: [1, 2, 3, 4, 5, 6]
    System.out.println(Arrays.toString(arr));
}

*附：交换的技巧

一般来说，交换数组中两个数字的函数如下:

int temp = a;
a = b;
b = temp;

但在大厂面试中，有一道非常经典的数字交换题目：如何在不引入第三个中间变量的情况下，完成两个数字的交换。
这里可以用到一个数学上的技巧：

a = a + b;
b = a - b;
a = a - b;

除了这种先加后减的写法，还有一种先减后加的写法：

a = b - a;
b = b - a;
a = a + b;

但这两种方式都可能导致数字越界。
更好的方案是通过位运算完成数字交换：

a = a ^ b;
b = b ^ a;
a = a ^ b;

时间复杂度 & 空间复杂度

冒泡排序从 1956 年就有人开始研究，之后经历过多次优化。它的空间复杂度为 O(1)，时间复杂度为 O*(n^2)，第二种、第三种冒泡排序由于经过优化，最好的情况下只需要O(*n) 的时间复杂度。

最好情况：在数组已经有序的情况下，只需遍历一次，由于没有发生交换，排序结束。

最差情况：数组顺序为逆序，每次比较都会发生交换。

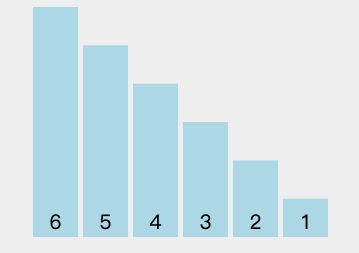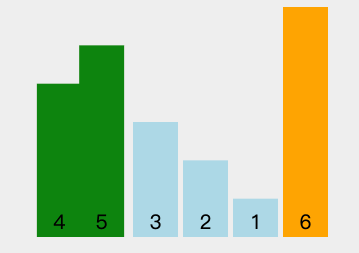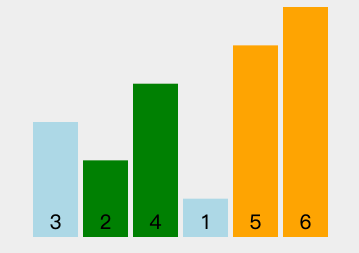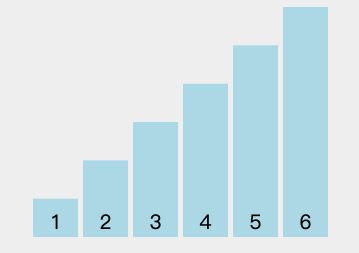
但优化后的冒泡排序平均时间复杂度仍然是 O*(*n^2)，所以这些优化对算法的性能并没有质的提升。

A 选择排序

选择排序的思想是：双重循环遍历数组，每经过一轮比较，找到最小元素的下标，将其交换至首位。

代码示例

public static void selectionSort(int[] arr) {
    int minIndex;
    for (int i = 0; i < arr.length - 1; i++) {
        minIndex = i;
        for (int j = i + 1; j < arr.length; j++) {
            if (arr[minIndex] > arr[j]) {
                // 记录最小值的下标
                minIndex = j;
            }
        }
        // 将最小元素交换至首位
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
    }
}

选择排序就好比第一个数字站在擂台上，大吼一声：“还有谁比我小？”。剩余数字来挨个打擂，如果出现比第一个数字小的数，则新的擂主产生。每轮打擂结束都会找出一个最小的数，将其交换至首位。经过 n-1 轮打擂，所有的数字就按照从小到大排序完成了。

动图演示

图中可以看出，每一轮排序都找到了当前的最小值，这个最小值就是被选中的数字，将其交换至本轮首位。这就是「选择排序法」名称的由来。

正是由于它比较容易理解，许多初学者在排序时非常喜欢使用选择排序法。

冒泡排序和选择排序的异同

相同点：

• 都是两层循环，时间复杂度都为 O*(*n^2);
• 都只使用有限个变量，空间复杂度 O*(1)。

不同点：

• 冒泡排序在比较过程中就不断交换；而选择排序增加了一个变量保存最小值 / 最大值的下标，遍历完成后才交换，减少了交换次数。

事实上，冒泡排序和选择排序还有一个非常重要的不同点，那就是：

• 冒泡排序法是稳定的，选择排序法是不稳定的。

想要理解这点不同，我们先要知道什么是排序算法的稳定性。

排序算法的稳定性

假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i] = r[j]，且 r[i] 在 r[j] 之前，而在排序后的序列中，r[i] 仍在 r[j] 之前，则称这种排序算法是稳定的；否则称为不稳定的。

理解了稳定性的定义后，我们就能分析出：冒泡排序中，只有左边的数字大于右边的数字时才会发生交换，相等的数字之间不会发生交换，所以它是稳定的。

而选择排序中，最小值和首位交换的过程可能会破坏稳定性。比如数列：[2, 2, 1]，在选择排序中第一次进行交换时，原数列中的两个 2 的相对顺序就被改变了，因此，我们说选择排序是不稳定的。

那么排序算法的稳定性有什么意义呢？其实它只在一种情况下有意义：当要排序的内容是一个对象的多个属性，且其原本的顺序存在意义时，如果我们需要在二次排序后保持原有排序的意义，就需要使用到稳定性的算法。

举个例子，如果我们要对一组商品排序，商品存在两个属性：价格和销量。当我们按照价格从高到低排序后，要再按照销量对其排序，这时，如果要保证销量相同的商品仍保持价格从高到低的顺序，就必须使用稳定性算法。

当然，算法的稳定性与具体的实现有关。在修改比较的条件后，稳定性排序算法可能会变成不稳定的。如冒泡算法中，如果将「左边的数大于右边的数，则交换」这个条件修改为「左边的数大于或等于右边的数，则交换」，冒泡算法就变得不稳定了。

同样地，不稳定排序算法也可以经过修改，达到稳定的效果。思考一下，选择排序算法如何实现稳定排序呢？

实现的方式有很多种，这里给出一种最简单的思路：新开一个数组，将每轮找出的最小值依次添加到新数组中，选择排序算法就变成稳定的了。

但如果将寻找最小值的比较条件arr[minIndex] > arr[j]修改为arr[minIndex] >= arr[j]，即使新开一个数组，选择排序算法依旧是不稳定的。所以分析算法的稳定性时，需要结合具体的实现逻辑才能得出结论，我们通常所说的算法稳定性是基于一般实现而言的。

二元选择排序

选择排序算法也是可以优化的，既然每轮遍历时找出了最小值，何不把最大值也顺便找出来呢？这就是二元选择排序的思想。

使用二元选择排序，每轮选择时记录最小值和最大值，可以把数组需要遍历的范围缩小一倍。

代码演示

public static void selectionSort2(int[] arr) {
    int minIndex, maxIndex;
    // i 只需要遍历一半
    for (int i = 0; i < arr.length / 2; i++) {
        minIndex = i;
        maxIndex = i;
        for (int j = i + 1; j < arr.length - i; j++) {
            if (arr[minIndex] > arr[j]) {
                // 记录最小值的下标
                minIndex = j;
            }
            if (arr[maxIndex] < arr[j]) {
                // 记录最大值的下标
                maxIndex = j;
            }
        }
        // 如果 minIndex 和 maxIndex 都相等，那么他们必定都等于 i，且后面的所有数字都与 arr[i] 相等，此时已经排序完成
        if (minIndex == maxIndex) break;
        // 将最小元素交换至首位
        int temp = arr[i];
        arr[i] = arr[minIndex];
        arr[minIndex] = temp;
        // 如果最大值的下标刚好是 i，由于 arr[i] 和 arr[minIndex] 已经交换了，所以这里要更新 maxIndex 的值。
        if (maxIndex == i) maxIndex = minIndex;
        // 将最大元素交换至末尾
        int lastIndex = arr.length - 1 - i;
        temp = arr[lastIndex];
        arr[lastIndex] = arr[maxIndex];
        arr[maxIndex] = temp;
    }
}

我们使用 minIndex 记录最小值的下标，maxIndex 记录最大值的下标。每次遍历后，将最小值交换到首位，最大值交换到末尾，就完成了排序。

由于每一轮遍历可以排好两个数字，所以最外层的遍历只需遍历一半即可。

二元选择排序中有一句很重要的代码，它位于交换最小值和交换最大值的代码中间：

if (maxIndex == i) maxIndex = minIndex;

这行代码的作用处理了一种特殊情况：如果最大值的下标等于 i，也就是说 arr[i] 就是最大值，由于 arr[i] 是当前遍历轮次的首位，它已经和 arr[minIndex] 交换了，所以最大值的下标需要跟踪到 arr[i] 最新的下标 minIndex。

二元选择排序的效率

在二元选择排序算法中，数组需要遍历的范围缩小了一倍。那么这样可以使选择排序的效率提升一倍吗？

从代码可以看出，虽然二元选择排序最外层的遍历范围缩小了，但 for 循环内做的事情翻了一倍。也就是说二元选择排序无法将选择排序的效率提升一倍。但实测会发现二元选择排序的速度确实比选择排序的速度快一点点，它的速度提升主要是因为两点：

• 在选择排序的外层 for 循环中，i 需要加到 arr.length - 1 ，二元选择排序中 i 只需要加到 arr.length / 2

• 在选择排序的内层 for 循环中，j 需要加到 arr.length ，二元选择排序中 j 只需要加到 arr.length - i

public class TestSelectionSort {
    public static void selectionSort(int[] arr) {
        int countI = 0;
        int countJ = 0;
        int countArr = 0;
        int minIndex;
        countI++;
        for (int i = 0; i < arr.length - 1; i++, countI++) {
            minIndex = i;
            countJ++;
            for (int j = i + 1; j < arr.length; j++, countJ++) {
                if (arr[minIndex] > arr[j]) {
                    // 记录最小值的下标
                    minIndex = j;
                }
                countArr++;
            }
            // 将最小元素交换至首位
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
        }
        int count = countI + countJ + countArr;
        System.out.println("selectionSort: countI = " + countI + ", countJ = " + countJ + ", countArr = " + countArr + ", count = " + count);
    }

    public static void selectionSort2(int[] arr) {
        int countI = 0;
        int countJ = 0;
        int countArr = 0;
        int minIndex, maxIndex;
        countI++;
        // i 只需要遍历一半
        for (int i = 0; i < arr.length / 2; i++, countI++) {
            minIndex = i;
            maxIndex = i;
            countJ++;
            for (int j = i + 1; j < arr.length - i; j++, countJ++) {
                if (arr[minIndex] > arr[j]) {
                    // 记录最小值的下标
                    minIndex = j;
                }
                if (arr[maxIndex] < arr[j]) {
                    // 记录最大值的下标
                    maxIndex = j;
                }
                countArr += 2;
            }
            // 如果 minIndex 和 maxIndex 都相等，那么他们必定都等于 i，且后面的所有数字都与 arr[i] 相等，此时已经排序完成
            if (minIndex == maxIndex) break;
            // 将最小元素交换至首位
            int temp = arr[i];
            arr[i] = arr[minIndex];
            arr[minIndex] = temp;
            // 如果最大值的下标刚好是 i，由于 arr[i] 和 arr[minIndex] 已经交换了，所以这里要更新 maxIndex 的值。
            if (maxIndex == i) maxIndex = minIndex;
            // 将最大元素交换至末尾
            int lastIndex = arr.length - 1 - i;
            temp = arr[lastIndex];
            arr[lastIndex] = arr[maxIndex];
            arr[maxIndex] = temp;
        }
        int count = countI + countJ + countArr;
        System.out.println("selectionSort2: countI = " + countI + ", countJ = " + countJ + ", countArr = " + countArr + ", count = " + count);
    }
}

在这个类中，我们用 countI 记录 i 的比较次数，countJ 记录 j 的比较次数，countArr 记录 arr 的比较次数，count 记录总比较次数。

测试用例：

import org.junit.Test;

import java.util.ArrayList;

public class UnitTest {
    @Test
    public void test() {
        ArrayList<Integer> list = new ArrayList<>();
        for (int i = 0; i <= 1000; i++) {
            // ArrayList 转 int[]
            int[] arr = list.stream().mapToInt(Integer::intValue).toArray();
            System.out.println("*** arr.length = " + arr.length + " ***");
            TestSelectionSort.selectionSort(arr);
            TestSelectionSort.selectionSort2(arr);
            list.add(i);
        }
    }
}

可以看到，二元选择排序中， arr 数组的比较次数甚至略高于选择排序的比较次数，整体是相差无几的。只是 i 和 j 的比较次数较少，正是在这两个地方提高了效率。

并且，在二元选择排序中，我们可以做一个剪枝优化，当 minIndex == maxIndex 时，说明后续所有的元素都相等，就好比班上最高的学生和最矮的学生一样高，说明整个班上的人身高都相同了。此时已经排序完成，可以提前跳出循环。通过这个剪枝优化，对于相同元素较多的数组，二元选择排序的效率将远远超过选择排序。

和选择排序一样，二元选择排序也是不稳定的。

时间复杂度 & 空间复杂度

前文已经说到，选择排序使用两层循环，时间复杂度为 O*(*n^2); 只使用有限个变量，空间复杂度 O(1)。二元选择排序虽然比选择排序要快，但治标不治本，二元选择排序中做的优化无法改变其时间复杂度，二元选择排序的时间复杂度仍然是 O(n^2)；只使用有限个变量，空间复杂度 O(1)。

LC 215. 数组中的第 K 个最大元素

分析

分析题目可知，我们不需要将数组中所有元素都排序。只用排 k 个数就可以了。这种只需要部分排序的场景，可以使用选择排序（或者下一章中介绍的堆排序）来完成。因为选择排序的过程是每次找出数组中的最大值（或最小值），依次将每个数字排好序。

本题的解题思路是，选择 k 次数组中的最大元素，将其交换到数组前面，然后返回数组的第 k 个元素即可。

由于新增了测试用例，选择排序无法再 AC 此题，请读者们学完堆排序后再来尝试本题。

代码

class Solution {
    public int findKthLargest(int[] nums, int k) {
        int maxIndex;
        // 执行 k 次选择
        for (int i = 0; i < k; i++) {
            maxIndex = i;
            for (int j = i + 1; j < nums.length; j++) {
                if (nums[maxIndex] < nums[j]) {
                    // 记录最大值的下标
                    maxIndex = j;
                }
            }
            // 将最大元素交换至首位
            swap(nums, i, maxIndex);
        }
        return nums[k - 1];
    }

    private static void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

}

A 插入排序

插入排序的思想非常简单，生活中有一个很常见的场景：在打扑克牌时，我们一边抓牌一边给扑克牌排序，每次摸一张牌，就将它插入手上已有的牌中合适的位置，逐渐完成整个排序。

插入排序有两种写法：

• 交换法：在新数字插入过程中，不断与前面的数字交换，直到找到自己合适的位置。
• 移动法：在新数字插入过程中，与前面的数字不断比较，前面的数字不断向后挪出位置，当新数字找到自己的位置后，插入一次即可。

交换法插入排序

不打牌的好孩纸直接看代码：

public static void insertSort(int[] arr) {
    // 从第二个数开始，往前插入数字
    for (int i = 1; i < arr.length; i++) {
        // j 记录当前数字下标
        int j = i;
        // 当前数字比前一个数字小，则将当前数字与前一个数字交换
        while (j >= 1 && arr[j] < arr[j - 1]) {
            swap(arr, j, j - 1);
            // 更新当前数字下标
            j--;
        }
    }
}
private static void swap(int[] arr, int i, int j) {
    int temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

当数字少于两个时，不存在排序问题，当然也不需要插入，所以我们直接从第二个数字开始往前插入。

整个过程就像是已经有一些数字坐成了一排，这时一个新的数字要加入，这个新加入的数字原本坐在这一排数字的最后一位，然后它不断地与前面的数字比较，如果前面的数字比它大，它就和前面的数字交换位置。

移动法插入排序

我们发现，在交换法插入排序中，每次交换数字时，swap 函数都会进行三次赋值操作。但实际上，新插入的这个数字并不一定适合与它交换的数字所在的位置。也就是说，它刚换到新的位置上不久，下一次比较后，如果又需要交换，它马上又会被换到前一个数字的位置。

由此，我们可以想到一种优化方案：让新插入的数字先进行比较，前面比它大的数字不断向后移动，直到找到适合这个新数字的位置后，新数字只做一次插入操作即可。

这种方案我们需要把新插入的数字暂存起来，代码如下：

public static void insertSort(int[] arr) {
    // 从第二个数开始，往前插入数字
    for (int i = 1; i < arr.length; i++) {
        int currentNumber = arr[i];
        int j = i - 1;
        // 寻找插入位置的过程中，不断地将比 currentNumber 大的数字向后挪
        while (j >= 0 && currentNumber < arr[j]) {
            arr[j + 1] = arr[j];
            j--;
        }
        // 两种情况会跳出循环：1. 遇到一个小于或等于 currentNumber 的数字，跳出循环，currentNumber 就坐到它后面。
        // 2. 已经走到数列头部，仍然没有遇到小于或等于 currentNumber 的数字，也会跳出循环，此时 j 等于 -1，currentNumber 就坐到数列头部。
        arr[j + 1] = currentNumber;
    }
}

整个过程就像是已经有一些数字坐成了一排，这时一个新的数字要加入，所以这一排数字不断地向后腾出位置，当新的数字找到自己合适的位置后，就可以直接坐下了。重复此过程，直到排序结束。

动图演示：

分析可知，插入排序的过程不会破坏原有数组中相同关键字的相对次序，所以插入排序是一种稳定的排序算法。

时间复杂度 & 空间复杂度
插入排序过程需要两层循环，时间复杂度为 O(n^2);只需要常量级的临时变量，空间复杂度为 O(1)。

A 小结

本章我们介绍了三种基础排序算法：冒泡排序、选择排序、插入排序。

冒泡排序
冒泡排序有两种优化方式：

• 记录当前轮次是否发生过交换，没有发生过交换表示数组已经有序；

• 记录上次发生交换的位置，下一轮排序时只比较到此位置。

选择排序
选择排序可以演变为二元选择排序：

• 二元选择排序：一次遍历选出两个值——最大值和最小值；
• 二元选择排序剪枝优化：当某一轮遍历出现最大值和最小值相等，表示数组中剩余元素已经全部相等。

插入排序
插入排序有两种写法：

• 交换法：新数字通过不断交换找到自己合适的位置；

• 移动法：旧数字不断向后移动，直到新数字找到合适的位置。

相同点

• 时间复杂度都是 O(n^2 ) ，空间复杂度都是 O(1)。
• 都需要采用两重循环。

不同点

• 选择排序是不稳定的，冒泡排序、插入排序是稳定的；
• 在这三个排序算法中，选择排序交换的次数是最少的；
• 在数组几乎有序的情况下，插入排序的时间复杂度接近线性级别。

2.时间复杂度 O(nlogn) 级排序算法

A 希尔排序

1959 年 7 月，美国辛辛那提大学的数学系博士 Donald Shell 在 《ACM 通讯》上发表了希尔排序算法，成为首批将时间复杂度降到 O(n^2 )。以下的算法之一。虽然原始的希尔排序最坏时间复杂度仍然是O(n^2 ) ，但经过优化的希尔排序可以达到 O(n^1.3) 甚至 O(n ^7/6 )。略为遗憾的是，所谓「一将功成万骨枯」，希尔排序和冒泡、选择、插入等排序算法一样，逐渐被快速排序所淘汰，但作为承上启下的算法，不可否认的是，希尔排序身上始终闪耀着算法之美。

希尔排序本质上是对插入排序的一种优化，它利用了插入排序的简单，又克服了插入排序每次只交换相邻两个元素的缺点。它的基本思想是：

• 将待排序数组按照一定的间隔分为多个子数组，每组分别进行插入排序。这里按照间隔分组指的不是取连续的一段数组，而是每跳跃一定间隔取一个值组成一组
• 逐渐缩小间隔进行下一轮排序
• 最后一轮时，取间隔为 1，也就相当于直接使用插入排序。但这时经过前面的「宏观调控」，数组已经基本有序了，所以此时的插入排序只需进行少量交换便可完成

动图演示

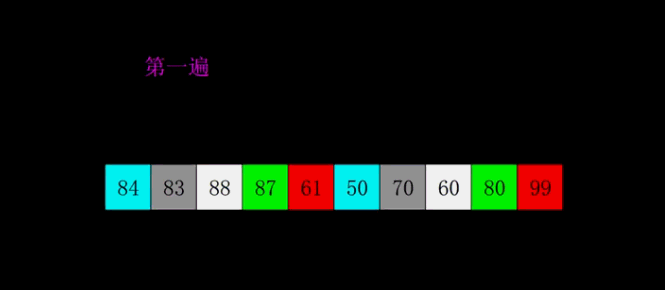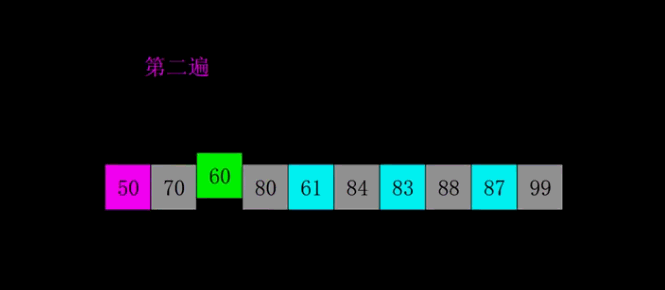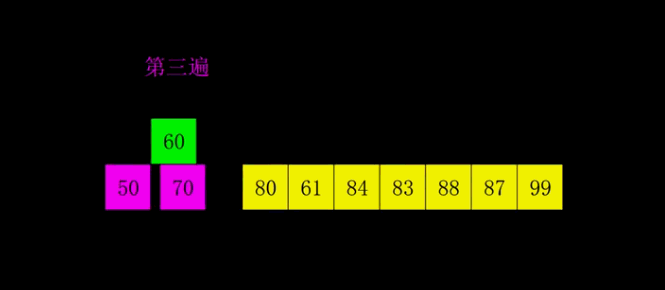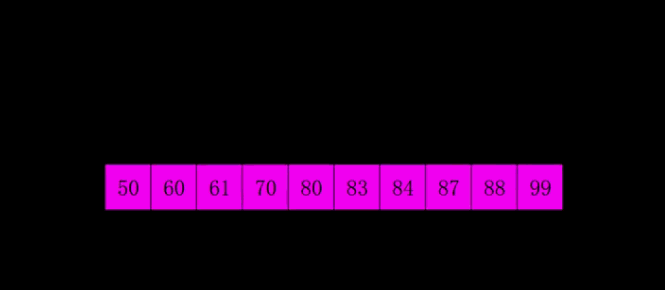
public static void shellSort(int[] arr) {
    // 间隔序列，在希尔排序中我们称之为增量序列
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        // 分组
        for (int groupStartIndex = 0; groupStartIndex < gap; groupStartIndex++) {
            // 插入排序
            for (int currentIndex = groupStartIndex + gap; currentIndex < arr.length; currentIndex += gap) {
                // currentNumber 站起来，开始找位置
                int currentNumber = arr[currentIndex];
                int preIndex = currentIndex - gap;
                while (preIndex >= groupStartIndex && currentNumber < arr[preIndex]) {
                    // 向后挪位置
                    arr[preIndex + gap] = arr[preIndex];
                    preIndex -= gap;
                }
                // currentNumber 找到了自己的位置，坐下
                arr[preIndex + gap] = currentNumber;
            }
        }
    }
}

注：由于希尔排序理解起来有一定的难度，所以笔者采用了更准确的命名方式替代 i、j 等变量名。

这份代码与我们上文中提到的思路是一模一样的，先分组，再对每组进行插入排序。同样地，这里的插入排序也可以采用交换元素的方式。

实际上，这段代码可以优化一下。我们现在的处理方式是：处理完一组间隔序列后，再回来处理下一组间隔序列，这非常符合人类思维。但对于计算机来说，它更喜欢从第 gap 个元素开始，按照顺序将每个元素依次向前插入自己所在的组这种方式。虽然这个过程看起来是在不同的间隔序列中不断跳跃，但站在计算机的角度，它是在访问一段连续数组。

public static void shellSort(int[] arr) {
    // 间隔序列，在希尔排序中我们称之为增量序列
    for (int gap = arr.length / 2; gap > 0; gap /= 2) {
        // 从 gap 开始，按照顺序将每个元素依次向前插入自己所在的组
        for (int i = gap; i < arr.length; i++) {
            // currentNumber 站起来，开始找位置
            int currentNumber = arr[i];
            // 该组前一个数字的索引
            int preIndex = i - gap;
            while (preIndex >= 0 && currentNumber < arr[preIndex]) {
                // 向后挪位置
                arr[preIndex + gap] = arr[preIndex];
                preIndex -= gap;
            }
            // currentNumber 找到了自己的位置，坐下
            arr[preIndex + gap] = currentNumber;
        }
    }
}

经过优化之后，这段代码看起来就和插入排序非常相似了，区别仅在于希尔排序最外层嵌套了一个缩小增量的 for 循环；并且插入时不再是相邻数字挪动，而是以增量为步长挪动。

增量序列

上文说到，增量序列的选择会极大地影响希尔排序的效率。增量序列如果选得不好，希尔排序的效率可能比插入排序效率还要低，举个例子：

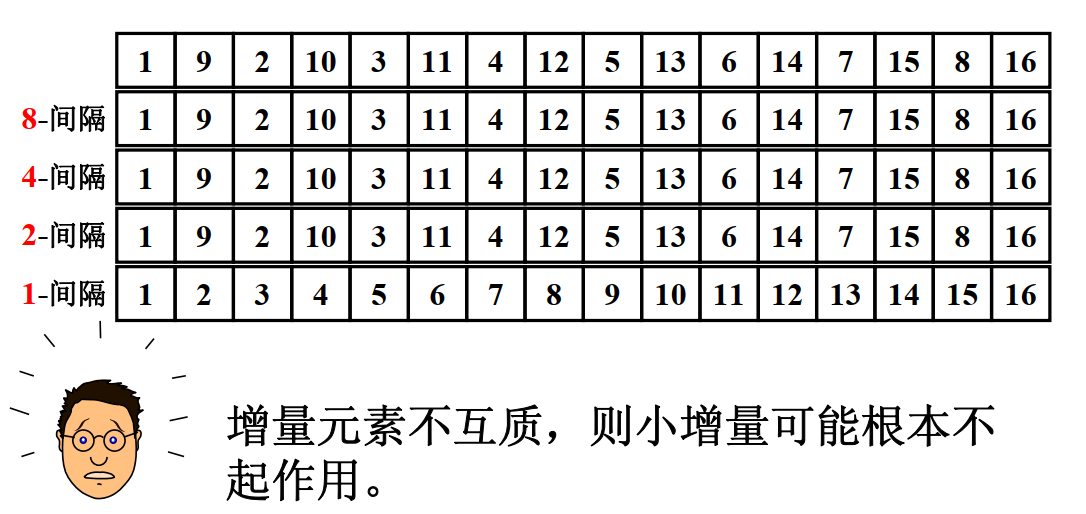
在这个例子中，我们发现，原数组 8 间隔、4 间隔、2 间隔都已经有序了，使用希尔排序时，真正起作用的只有最后一轮 1 间隔排序，也就是直接插入排序。希尔排序反而比直接使用插入排序多执行了许多无用的逻辑。

于是人们发现：增量元素不互质，则小增量可能根本不起作用。

事实上，希尔排序的增量序列如何选择是一个数学界的难题，但它也是希尔排序算法的核心优化点。数学界有不少的大牛做过这方面的研究。比较著名的有 Hibbard 增量序列、Knuth 增量序列、Sedgewick 增量序列。

以 Knuth 增量序列为例，Knuth 就是上篇文章中吐槽冒泡算法的那个数学家 Donald E. Knuth，使用 Knuth 序列进行希尔排序的代码如下：

public static void shellSortByKnuth(int[] arr) {
    // 找到当前数组需要用到的 Knuth 序列中的最大值
    int maxKnuthNumber = 1;
    while (maxKnuthNumber <= arr.length / 3) {
        maxKnuthNumber = maxKnuthNumber * 3 + 1;
    }
    // 增量按照 Knuth 序列规则依次递减
    for (int gap = maxKnuthNumber; gap > 0; gap = (gap - 1) / 3) {
        // 从 gap 开始，按照顺序将每个元素依次向前插入自己所在的组
        for (int i = gap; i < arr.length; i++) {
            // currentNumber 站起来，开始找位置
            int currentNumber = arr[i];
            // 该组前一个数字的索引
            int preIndex = i - gap;
            while (preIndex >= 0 && currentNumber < arr[preIndex]) {
                // 向后挪位置
                arr[preIndex + gap] = arr[preIndex];
                preIndex -= gap;
            }
            // currentNumber 找到了自己的位置，坐下
            arr[preIndex + gap] = currentNumber;
        }
    }
}

先根据数组的长度，计算出需要用到的 Knuth 序列中的最大增量值，然后根据 Knuth 序列的规则依次缩小增量，从高增量到低增量分别进行排序。

测试：

@Test
public void test() {
    int[] arr = new int[]{6, 2, 1, 3, 5, 4};
    shellSortByKnuth(arr);
    // 输出: [1, 2, 3, 4, 5, 6]
    System.out.println(Arrays.toString(arr));
}

使用 Knuth 序列的希尔排序，时间复杂度已经降到了 O*(*n^2) 以下。但具体时间复杂度是多少，尚未有明确的证明，数学界仅仅是猜想它的平均时间复杂度为 (n^3/2)。

虽然插入排序是稳定的排序算法，但希尔排序是不稳定的。在增量较大时，排序过程可能会破坏原有数组中相同关键字的相对次序。

时间复杂度 & 空间复杂度

事实上，希尔排序时间复杂度非常难以分析，它的平均复杂度界于 O(n) 到 O(n^2) 之间，普遍认为它最好的时间复杂度为 O(n ^1.3 )。

希尔排序的空间复杂度为 O(1)，只需要常数级的临时变量。

**希尔排序与 O(n^2) 级排序算法的本质区别

相对于前面介绍的冒泡排序、选择排序、插入排序来说，希尔排序的排序过程显得较为复杂，希望读者还没有被绕晕。接下来我们来分析一个有趣的问题：希尔排序凭什么可以打破时间复杂度 O(n^2 ) 的魔咒呢？它和之前介绍的O(n^2 ) 级排序算法的本质区别是什么？

只要理解了这一点，我们就能知道为什么希尔排序能够承上启下，启发出之后的一系列 O(n^2 ) 级以下的排序算法。

这个问题我们可以用逆序对来理解。

当我们从小到大排序时，在数组中的两个数字，如果前面一个数字大于后面的数字，则这两个数字组成一个逆序对。

排序算法本质上就是一个消除逆序对的过程。

对于随机数组，逆序对的数量是 O(n^2 ) 级的，如果采用「交换相邻元素」的办法来消除逆序对，每次最多只能消除一组逆序对，因此必须执行 O(n^2 ) 级的交换次数，这就是为什么冒泡、插入、选择算法只能到
O(n^2 )级的原因。反过来说，基于交换元素的排序算法要想突破
O(n^2 ) 级，必须通过一些比较，交换间隔比较远的元素，使得一次交换能消除一个以上的逆序对。

希尔排序算法就是通过这种方式，打破了在空间复杂度为 O(1) 的情况下，时间复杂度为 O(n^2 )的魔咒，此后的快排、堆排等等算法也都是基于这样的思路实现的。

注：

1.虽然约翰·冯·诺伊曼在 1945 年提出的归并排序已经达到了
O(nlogn) 的时间复杂度，但归并排序的空间复杂度为 O(n)，采用的是空间换时间的方式突破 O(n^2 )。

2.希尔排序在面试或是实际应用中都很少遇到，读者仅需了解即可。