状态压缩DP 图文详解（二）

前言:

本文是讲解状态压缩DP的第二节，仍然是对基于连通性问题的探讨与学习。

一些概念性的问题，以及基本解法 在第一节中讲过，这里就不再赘述。

(20条消息) 状态压缩DP 图文详解（一）_Dream.Luffy的博客-CSDN博客

对典例 蒙德里安的梦想 的分析

直接看例题：

求把 N×M 的棋盘分割成若干个 1×2 的长方形，有多少种方案。

例如当 N=2，M=4 时，共有 5 种方案。当 N=2，M=3 时，共有 3 种方案。

如下图所示：

输入格式

输入包含多组测试用例。

每组测试用例占一行，包含两个整数 N 和 M。

当输入用例 N=0，M=0 时，表示输入终止，且该用例无需处理。

输出格式

每个测试用例输出一个结果，每个结果占一行。

数据范围

1≤N,M≤11

输入样例：

1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0

输出样例：

1
0
1
2
3
5
144
51205

算法分析:
 1.拿到题目，我们先从暴力的角度思考，如果我们暴力枚举每一个格子，那么时间复杂度为2^121, 是会超时的，因此考虑用记忆化搜索来优化， 于是我们用动态规划来考虑这个问题。

性质挖掘：

2.同时，这里我们可以发现一个性质：先将所有横着的小方块摆满再放竖着的小方块，方案数和总方案数是相等的，因为当所有横着的合法小方块放完后，竖着的小方块只需往空里塞即可，这一点可以从样例观察到。

即核心：先放横着的，再放竖着的

3.若我们按列枚举放小方块，可以发现，

①在第i列放横着小方块的方案会受到第i - 1列的影响

②并且若在同一个状态i中，上一个小方块和下一个小方块之间的空格数为奇数时是不合法的（因为空格数奇数个时无法用竖着的小方格塞满棋盘，会留下空缺）

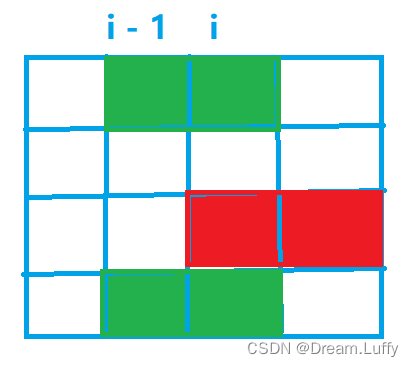
第一种情况，如下图：

若两个方块重叠时则该方案是不合法的（图中为合法情况），

这里我们设 第i - 1列的方块的摆放方案状态为 k， 第i 列方块的摆放方案为 j

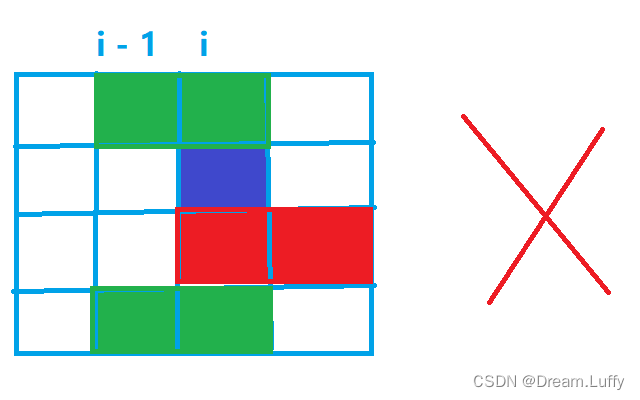
第二种情况:

 第一种方案是不合法的，因为在状态 j 和状态k ， 中间的空格数为奇数，不能放下竖着的(1 x 2)小方块

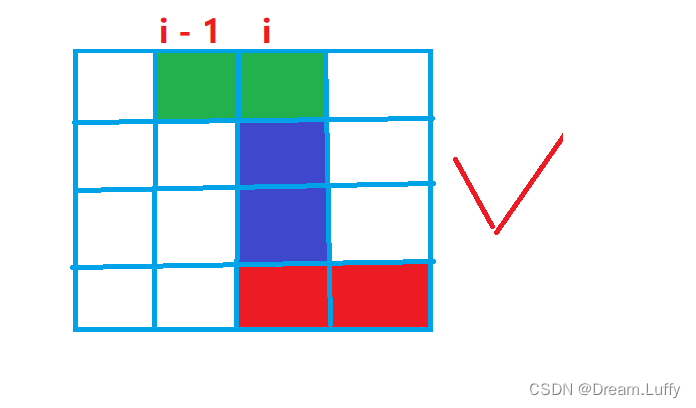
第二种方案则是合法的 :

 

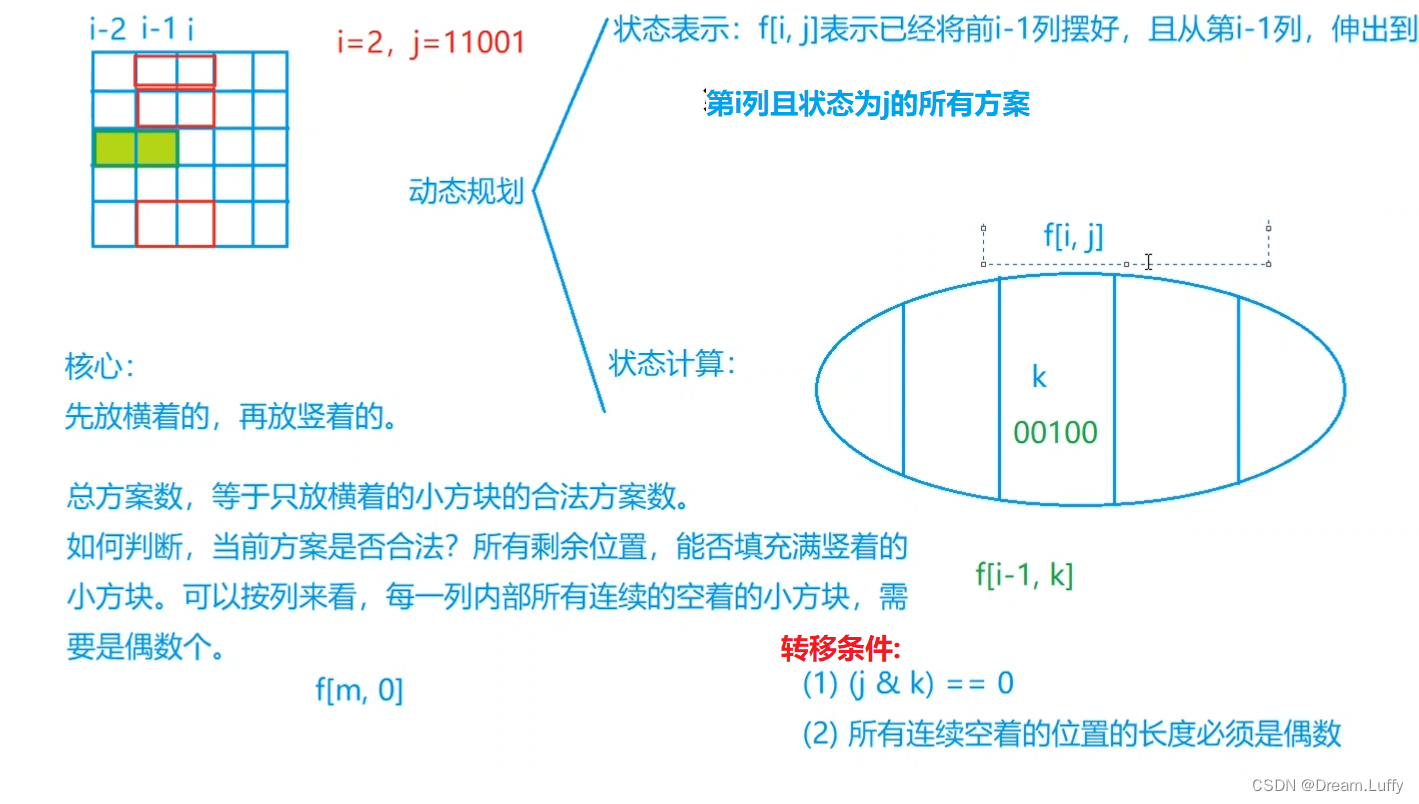
4..接下来，我们思考动态规划的一般流程: 状态表示，以及状态计算

首先是 状态表示 根据前文的分析，我们这里需要维护的变量只有三个

①当前在哪一列，

②当前列的状态是什么

③当前状态方案数

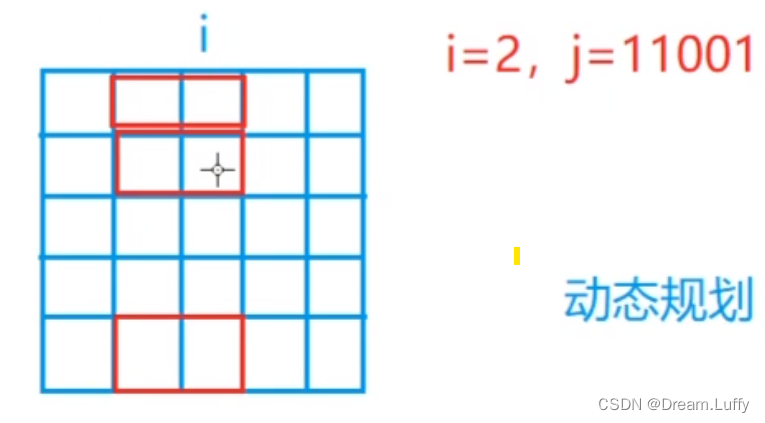
所以我们可以定义状态表示为f[i][j]

状态表示: f[i][j] 表示已经将前i - 1列摆好，且从第 i - 1 列伸出到第i 列的状态为j 的所有方案

接下来是 状态计算 由于我们要找的是最后一个状态的不同点，而第i - 1列伸到第 i 列的状态 j 是固定的， 没有固定的是第i - 2列伸到第 i - 1列的状态。

于是，集合的划分依据应是：i - 2 列延申 到i - 1 列的状态k 来划分的

那么，我们上面的图就应该有所更新，表示为：

这时，我们设第i - 2列的方块的摆放方案状态为 k， 第i - 1列方块的摆放方案为 j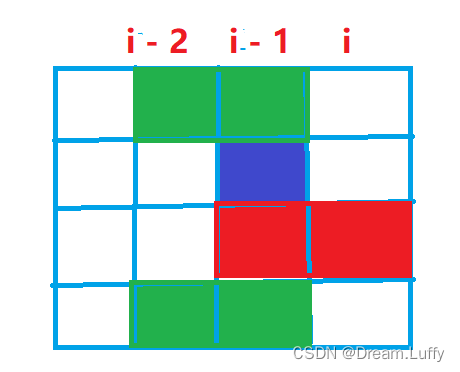

 此时，我们的集合划分图像应当如下

至此，完成所有分析,整体如下:

 代码如下:
 

#include<iostream>
#include<cstring>
#include<algorithm>
#include<vector>
using namespace std;
							//N表行数 
const int N = 12, M = 1 << N;//M表方案数，一共有二的N次方个 

int n, m;
long long f[N][M]; //状态转移方程
vector<int> state[M];  //存储所有合法状态 
bool st[M]; //存储每种状态是否有奇数个连续的0，如果奇数个0是无效状态
			//如果是偶数个零置为true。


int main()
{
	while(cin >> n >> m, n ||m)//本题有多个数据 
	{
		//第一部分：预处理1
		//对于每种状态，先预处理每列不能有奇数个0 
		for(int i = 0;i < 1 << n;i ++)//预处理st数组,判断所有连续的0是否有偶数个		 
		{
			int cnt = 0;//cnt 表示0的个数
			bool is_valid = true;//是否合法 
			 for(int j = 0;j < n;j ++)//遍历这一列，从上到下 
			 if(i >> j & 1)//对于i的二进制数的第j位,判断是否为1 
			 {
			 	if(cnt & 1)//判断前面的0是否有奇数个 
			 	{
			 		is_valid = false;//不合法 
			 		break;
				 }
				 cnt = 0;//清空 
			  } 
			  else cnt ++;//否则前面是0，cnt++ 
			  if(cnt & 1) is_valid = false;//判断最下面那一段连续0的个数 
			  st[i] = is_valid;
		}
		
	//第二部分：预处理2
	//判断第i - 2列伸出来的和第i - 1列伸出去的是否冲突
	
	for(int j = 0;j < 1 << n;j ++)//对于第i列的所有状态
	{
		state[j].clear();//清空上次操作遗留的状态(因为本题有while循环，多个测试数据)
		for(int k = 0;k < 1 << n;k ++)//对于第i-1列的所有状态 
		{
			if((j & k)==0 && st[j | k])//若两者伸出来的没重叠
				state[j].push_back(k);//j | k表示当前第i- 1列到底有几个1，即哪几行是放格子的 
									
		 } 
	}
	
	//第三部分：DP
	memset(f,0,sizeof f); //全部初始化为0，因为是while连续读入 
	
	f[0][0] = 1;//这里没有-1列，所以不可能有方块伸到第0列，因此f[0][0] = 1, 即表示棋盘为空的一种状态 
	
	for(int i =1;i <= m;i ++)//遍历每一列:第i列合法范围是(0~m-1列) 
		for(int j = 0;j < 1 << n;j ++)//遍历当前列（i）的所有状态j 
			for(auto k: state[j])//遍历第i-1列的状态k,真正满足则转移 
				f[i][j] += f[i - 1][k];// 当前列的方案数就等于之前的第i-1列所有状态k的累加。
	
	//依据状态表示的定义:f[m][0]表示 前m-1列都处理完，并且第m-1列没有伸出来的所有方案数。
	//即整个棋盘处理完的方案数 
	cout << f[m][0] << endl;			
	}
	
	
	return 0;
}

注：第一部分的预处理，对应上面分析的第二种情况， 

第二部分的预处理，对应上面分析的第一种情况:

该系列会持续更新, 我是Luffy，期待与你再次相遇