【C语言】算法学习·KMP算法

KMP算法（全称Knuth-Morris-Pratt字符串查找算法，由三位发明者的姓氏命名）是可以在文本串s中快速查找模式串p的一种算法。

要想知道KMP算法是如何减少字符串查找的时间复杂度的，我们不如来看暴力匹配方法是如何浪费时间的。所谓暴力匹配，就是逐字符逐字符地进行匹配（比较s[i]和p[j]），如果当前字符匹配成功（s[i]==p[j]），就匹配下一个字符（++i, ++j），如果失配，i回溯，j置为0（i=i-j+1, j=0）。代码如下：

// 暴力匹配
int i = 0, j = 0;
while (i < s.length())
{
    if (s[i] == p[j])
        ++i, ++j;
    else
        i = i - j + 1, j = 0;
    if (j == p.length())  // 匹配成功
    {
        // 对s[i - j .. i - 1]进行一些操作
        cout << i - j << endl;
        i = i - j + 1;
        j = 0;
    }
}

举例来说，假如s="abababcabaa", 我们暴力匹配，过程会是怎样？

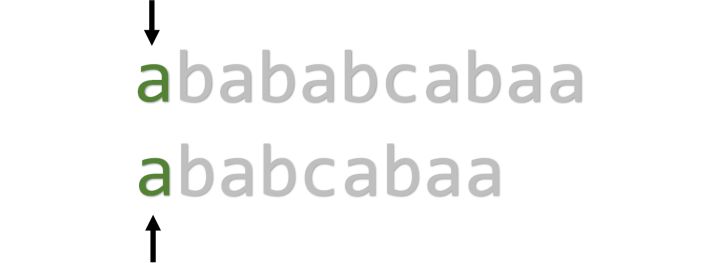
从头开始匹配，第一个字符是a，匹配成功。

第2~4个字符也匹配成功，继续。

下一位，匹配失败，回溯。

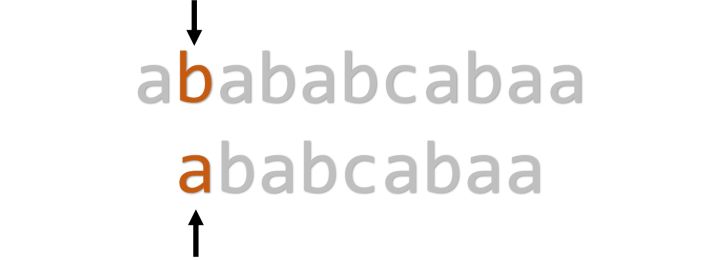
匹配失败，继续尝试。

下一位，匹配成功。

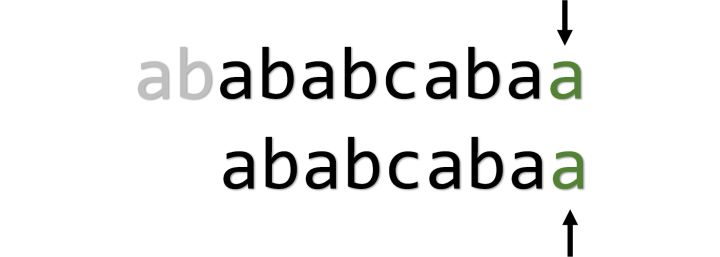
就这样一直匹配到结尾。

设两个字符串的长度分别为 N 和  M，则暴力匹配的最坏时间复杂度是O(nm)  。究其原因，在于i进行回溯浪费了时间。能不能让i不走回头路呢？然而，如果i不回溯，同时又把j置为0，很可能会出现缺漏，如下图。

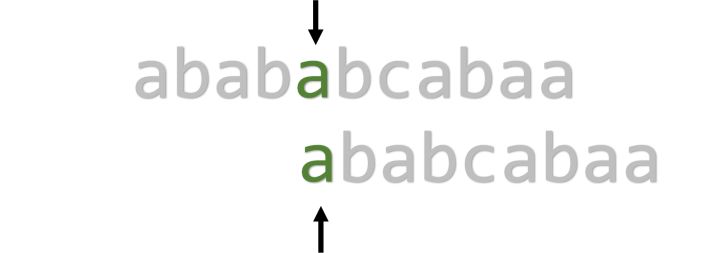
这样配下去会漏掉一个匹配

于是为了让j被赋为一个合适的值，我们引入了PMT（Partial Match Table，部分匹配表）。

---

j应该被赋值为多少，是只与模式串自身有关的。每个模式串，都对应着一张PMT，比如"ababcabaa"对应的PMT如下：

这是什么意思呢？简单地说，pmt[i]就是，从p[0]往后数、同时从p[i]往前数相同的位数，在保证前后缀相同的情况下，最多能数多少位。（但要小于p的长度）

专业点说，它是真前缀与真后缀的集合之交集中，最长元素的长度。（这里的“真”字与“真子集”中的“真”字类似）

为什么PMT可以用来确定j指针的位置呢？让我们先回到暴力匹配算法第一次失配时的情形：

这时，s中的'a'与p中的'c'没有配上，我们计划保持i指针（上面的指针）不变，而把j指针左移。我们注意到，"abab"已经匹配成功了，它拥有一个前缀"ab"，以及一个后缀"ab"（虚线部分），所以我们可以把这个"ab"利用起来，变成下面这样：

实际上这时我们正是在令j=pmt[j-1]。再举一个例子：

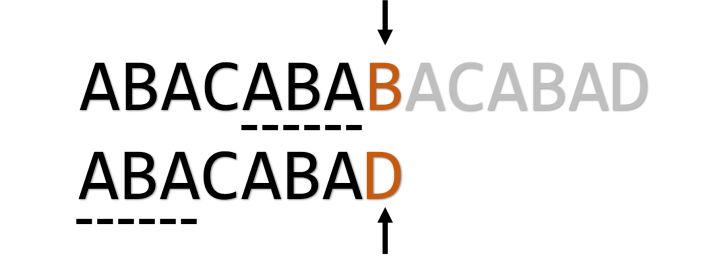
发生失配，我们令j=pmt[j-1](=3)（也就是符合条件的最长前缀所紧接着的下一位）：

仍不匹配，我们继续：

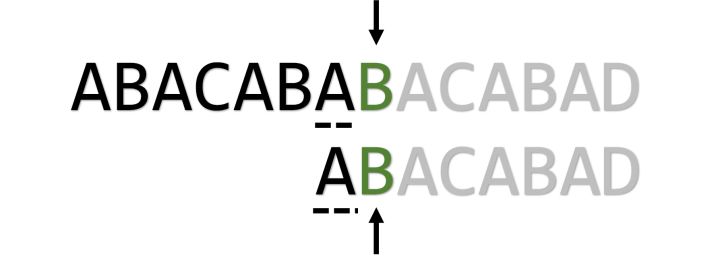
这次取得了成功。 当然，我们并不总是能成功，有可能j指针一路减到了0，但s[i]仍然不等于p[j]，这时我们不再移动j指针。

以上这些过程转换为代码是这样的：

for (int i = 0, j = 0; i < s.length(); ++i)
{
    while (j && s[i] != p[j]) j = pmt[j - 1]; // 不断前移j指针，直到成功匹配或移到头为止
    if (s[i] == p[j]) j++;  // 当前位匹配成功，j指针右移
    if (j == p.length())
    {
        // 对s[i - j + 1 .. i]进行一些操作
        j = pmt[j - 1];
    }
}

很多文章中会使用next数组，即把PMT整体向右移一位（特别地，令next[0]=-1），表示在每一位失配时应跳转到的索引。也就是说，失配时，按照i -> next[i] -> next[next[i]] -> ...的顺序跳转。其实原理和实现都是差不多的。

---

现在问题来了，PMT怎么求？如果暴力求的话，时间复杂度是 O(mm) ，并不理想。一种精妙的做法是，在错开一位后，让p自己匹配自己（这相当于是用前缀去匹配后缀）。我们知道pmt[0]=0，而之后的每一位则可以通过在匹配过程中记录j值得到。

还是以刚刚的模式串为例：

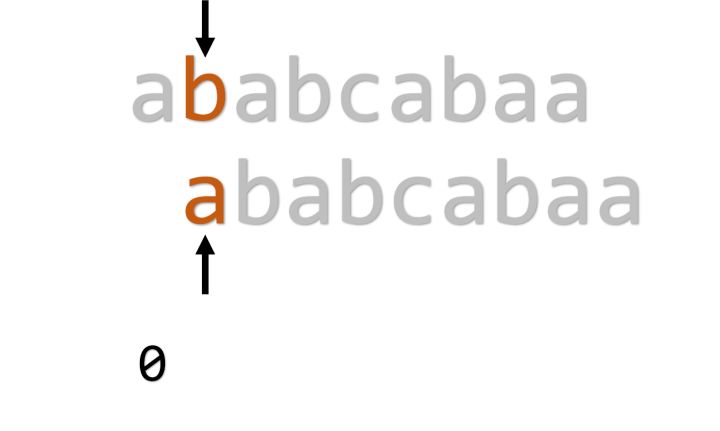
匹配失败，则pmt[1]=-1+1=0，i指针后移。

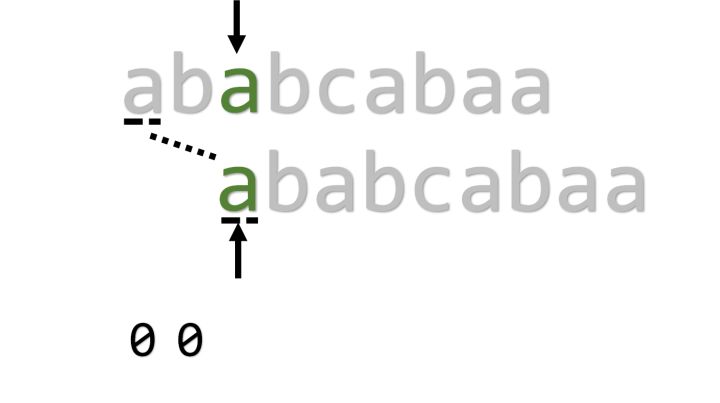
接下来匹配成功，j指针右移，可知pmt[2]=1，然后将两个指针都右移。

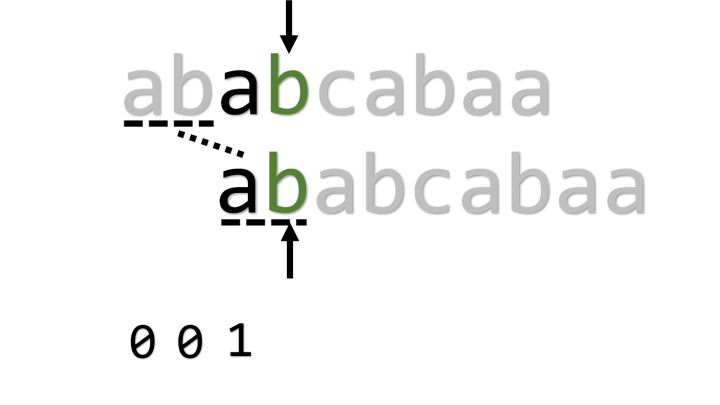
继续匹配成功，j指针右移，pmt[3]=2。

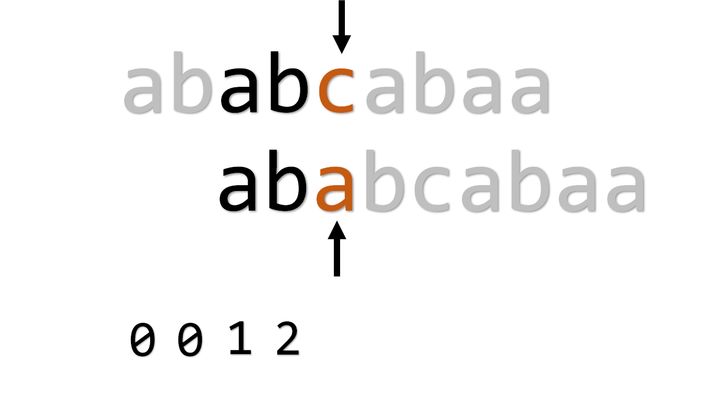
下一位失配，因为前面的pmt已经算出来了，我们可以像匹配文本串时那样地使用它。pmt[2-1]即pmt[1]等于0，所以退回到开头。

j指针已经到了开头，仍未匹配成功，所以不再移动，pmt[4]=j=0。

接下来也按这种方法操作：

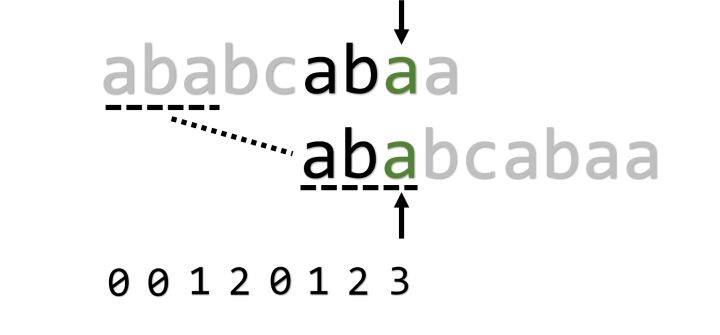
最后一位出现失配，这次我们先令j=pmt[j-1]=1：

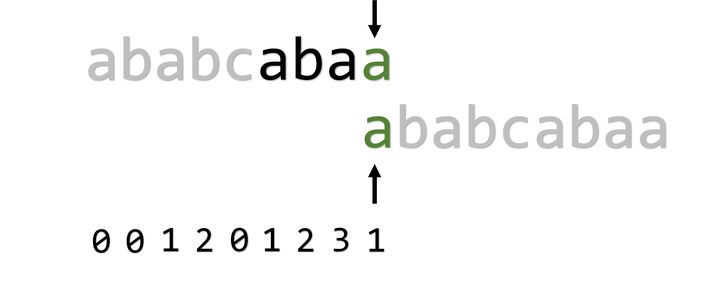
再次匹配，匹配成功，j指针右移一位，pmt[i]=j=1。自此，我们通过一趟自我匹配，求出了PMT，代码如下：

// pmt[0] = 0;
for (int i = 1, j = 0; i < plen; ++i)
{
    while (j && p[i] != p[j]) j = pmt[j - 1];
    if (p[i] == p[j]) j++;
    pmt[i] = j;
}

现在已经可以解决洛谷模板题了：

（洛谷P3375 【模板】KMP字符串匹配）

#include <bits/stdc++.h>
using namespace std;
const int MAXN = 1e6 + 5;
int pmt[MAXN];
void get_pmt(const string& s) {
    for (int i = 1, j = 0; i < s.length(); ++i) {
        while (j && s[i] != s[j]) j = pmt[j - 1];
        if (s[i] == s[j]) j++;
        pmt[i] = j;
    }
}
void kmp(const string& s, const string& p) {
    for (int i = 0, j = 0; i < s.length(); ++i) {
        while (j && s[i] != p[j]) j = pmt[j - 1];
        if (s[i] == p[j]) j++;
        if (j == p.length()) {
            cout << i - j + 2 << '\n'; // 因为要1-index，所以是+2
            j = pmt[j - 1];
        }
    }
}
int main() {
    ios::sync_with_stdio(false);
    string s, p;
    cin >> s >> p;
    get_pi(p);
    kmp(s, p);
    for (int i = 0; i < p.length(); ++i)
        cout << pmt[i] << ' ';
    return 0;
}

---

绝大多数情况下，上面的算法都够用了，所以很多人就管它叫KMP算法。但实际上，它只能称作MP算法，因为真正的KMP算法还有一个Knuth提出的常数优化。其实，这个真·KMP算法反而一般用不上，但这里也介绍一下。

例如对于"abababc"这个模式串，如果我们用它来匹配"abababd"，在最后处要跳转3次才能发现匹配失败：

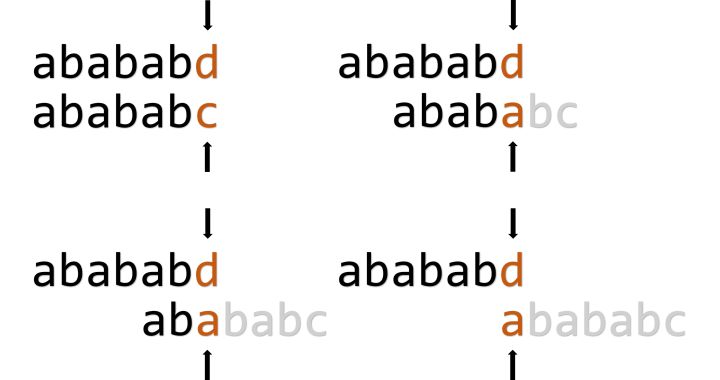
其实中间这几次跳转毫无意义，我们明知道d和a是不能匹配的，却做了很多无用功。所以我们可以在计算pmt时做一些小改动来避免这种情况。

例如上图这里，按道理匹配到这一步我们应该令pmt[i] = ++j (=2)。但是我们发现，p[i + 1]与p[j + 1]是相等的'a'。也就是说稍后在匹配时，假如j指针为4时失配（说明"ababa"无法匹配），那在j指针为2时肯定也会失配（因为"aba"也无法匹配）。所以我们不如把路径压缩一下——直接让pmt[i] = pmt[j] (=pmt[2-1])而不是++j (=2) ，跳过j指针为2的情况。

void get_pmt(const string& s) {
    for (int i = 1, j = 0; i < s.length(); ++i) {
        while (j && s[i] != s[j]) j = pi[j - 1];
        if (s[i] == s[j]) {
            if (s[i + 1] == s[j + 1])
                pmt[i] = pmt[j++];
            else
                pmt[i] = ++j;
        }
        else
            pmt[i] = j;
    }
}

其实这样得到的pmt数组已经不符合我们定义的PMT的性质了，如果较真的话可以换一个名字。

无论是MP算法还是KMP算法，其总时间复杂度都是 O(m+n) ，这是因为++i和++j都只进行了  次，虽然j在过程中有减小，但j在任何时刻不可能小于  ，所以j减小的次数也不可能超过  。