第六章 图

6_1

02、如何对无环有向图中的顶点号重新安排可使得该图的邻接矩阵中所有的1集中到对角线以上？

答：按顶点的出度进行排序。n个顶点的有向图，其顶点的最大出度是n-1,最小出度为0。排序后，出度最大的顶点编号为1，出度最小的顶点编号为n。之后，进行调整，只要存在弧<i,j>，就不管顶点j的出度是否大于顶点i的出度，都把i编号 在顶点j的变好之前，因为有i<=j，弧<i,j>对应的1才能出现在邻接矩阵的上三角。

6_2

04、写出从图的领接表表示转换成邻接矩阵表示的算法

//图的邻接表存储结构
typedef struct ArcNode{
	int adjvex;//该弧所指向的顶点的位置
	struct ArcNode *next;//指向下一条弧的指针
	//InfoType info; 
}ArcNode;
typedef struct VNode{
	VertexType data;//顶点信息 
	ArcNode *first;//指向第一条依附该顶点的弧的指针 
}VNode,AdjList[MaxVertexNum];
typedef struct{
	AdjList vertices;//相当于VNode vertices[MaxVertexNum]
	int vexnum,arcnum;//图的顶点数和弧数 
}ALGraph;//ALGraph是以领接表存储的图类型 

void Covert(ALGraph &G,int arcs[n][n])
{
	for(int i=0;i<n;i++)
	{
		p=G->vertices[i].first;//取出顶点i的第一条出边
		while(p!=NULL)
		{
			arcs[i][p->adjvex]=1;
			p=p->next;//取下一条边 
		 } 
	}
 } 

06、

//图的存储结构
typedef struct{
	int numVertices,numEdges;//图中实际的顶点数和边数 
	char Vertice[MAXV];//顶点表 MAXV为已定义常量 
	int Edge[MAXV][MAXV];//邻接矩阵 
}; 

//思路一:
//可以额外开一个数组来记录扫描Edge[][]中元素为1的个数 
//此时 时间复杂度为O(n2) 空间复杂度为O(n)

//思路二：边扫描 边记录 最后判断
int IsExist(MGraph G)
{
	int i,j;//双重循环用于遍历整个邻接矩阵
	int cnt=0,degree;//cnt记录度为奇数顶点的个数 degree记录每个顶点的度数
	
	for(i=0;i<G.vecnum;i++)
	{
		degree=0;//每次新一轮循环 都将degree重置为0 
		for(j=0;j<G.vecnum;j++)
			degree+=G.Edge[i][j];//第i个结点的度数 
		if(degree%2==1)//第i的结点的度数为奇数 
			cnt++;//个数加1 
	}
	
	if(cnt==0||cnt==2)
		return 1;//存在EL路径 
	else
		return 0; //不存在EL路径 
}

6_3

02、试设计一个算法，判断一个无向图G是否为一棵树。若是一棵树，则算法返回true，否则返回false。

//判断无向图是否是一棵树
//思路：无向图是无环或者边数为顶点数-1的连通图
//连通判断：选择一种遍历算法 若遍历完成后遍历顶点个数等于总的顶点数则是连通的

bool Judge_Is_Tree(Graph &G)
{
	for(int i=1;i<=G.vexnum;i++)
		visited[i]=false;//初始化visited数组
	int Vnum=0,Enum=0;//vnum保存遍历过程的顶点数 enum保存遍历过程中的边数
	//遍历整个图 
	DFS(G,1,Vnum,Enum,visited);
	
	if(Vnum==vexnum&&Enum==2*(G.vexnum-1))
		return true;
	else
		return false;	 
}

void DFS(Graph G,int v,int Vnum,int Enum,int visited[])
{
	visited[v]=true; Vnum++;//访问结点 Vnum+1 
	int w=FirstNeighbor(G,v);
	while(w!=-1)//存在邻接结点 则边数+1 
	{
		Enum++;//由于访问结点的时候 一条边对应两个结点 所以每条边会多加一次 边数是总的两倍 
		if(!visited[w])//当该邻接结点未被访问过 
			DFS(G,w,Vnum,Enum,visited);
		w=NextNeighbor(G,v,w);//找除v结点外的下一个邻接结点 
	}
 } 

03、写出图的深度优先搜索DFS算法的非递归算法（图采用邻接表形式）

//由于使用了栈 使得遍历方式从右端到左端进行 但仍是DFS序列 
void DFS(ALGraph G,int v)
{
	int w;
	for(int i=0;i<G.vexnum;i++)
		visited[i]=false;//初始化visited数组 
	InitStack(S);
	Push(S,v);//将第一个结点压入栈中 
	visited[v]=true;//置为已访问 
	
	while(!IsEmpty(S))
	{
		k=Pop(S);//栈中推出第一个顶点 
		visit(k);//出栈后访问 
		for(w=FirstNeighbor(G,k);w>=0;w=NextNeighbor(G,k,w))
		{
			if(!visited[w])
			{
				Push(S,w);//未访问过的结点 入栈
				visited[w]=true;
			}
		}

	}
}

04、分别采用基于深度优先遍历和广度优先遍历算法判别以邻接表方式存储的有向图中方是否存在由顶点Vi到顶点Vj的路径（i≠j）。注意算法中涉及的图的基本操作必须在此存储结构上实现

//思路:从i结点遍历图,若过程中遍历到某一结点与j相等 则说明存在这样一条路径

//使用DFS判断
int visited[MAXSIZE]={0};//初始化标技数组
void DFS(ALGraph G,int i,int j,bool reach)//使用递归 
{
	if(i==j)//遍历过程中遇到与j相等的结点 说明存在路径 
	{//相当于递归基 
		reach=true;
		return; 
	}
	visited[i]=1;//置已访问标记 
	for(int w=FirstNeighbor(G,i);w>=0;w=NextNeighbor(G,i,w))
		if(!visited[w]&&!reach)//未被访问过 且当前结点与j不等 
			DFS(G,w,j,reach); 
	
}

//使用BFS判断 
bool BFS(ALGraph G,int i,int j)
{
	InitQueue(Q);
	for(int i=0;i<G.vexnum;i++)
		visited[i]=false;
	Enqueue(Q,i);//将第一个结点入队 

	while(!QueueEmpty())
	{
		Dequeue(Q,u);//结点出队 
		visited[u]=true;//置已访问标记 
		for(int w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))
		{
			//寻找邻接结点过程中 如果w==j则存在这样一条路径 
			if(w==j) return true;//存在 返回true 
			if(!visited[w])
			{
				Enqueue(Q,w);//未被访问过 则入队 并置已访问标记 
				visited[w]=true;
			}	
		}
		
	}
	
 }

05、假设图用邻接表存储，设计一个算法，输出从顶点Vi到顶点Vj的所有简单路径。

//思路:用深度优先算法来遍历图中结点 若遍历到某一结点与j结点相同 则输出
//用path数组来存储Vi到Vj的路径

void FindPath_i_j(AlGraph G,int i,int j,int path[],int d)//d对应path数组下标 
{
	int w;
	ArcNode *p;
	d++;
	path[d]=i;//存储路径上的结点
	visited[i]=1;
	
	if(w==j)//找到了Vi到Vj的路径 
		print(path[]);
	
	p=G->adjlist[i].firstarc;//adjlist[]是顶点数组 
	while(p!=NULL)
	{
		//adjvex是顶点域 存储的是顶点值 
		w=p->adjvex;//若顶点w未访问 则递归访问它 
		if(!visited[w])//保证下一个结点未被访问过 从而是简单路径 
			FindPath_i_j(G,w,j,path,d);
		p=p->adjvex; 
	}
	visited[i]=0;//因为是找到所有简单路径 所以要恢复visited数组的初值 以便下一条路径寻找时使用 
 }

6_4

01、下面是一种称为“破圈法”的求解最小生成树的方法：

所谓”所谓破圈法“，是指”任取一圈，去掉圈上最大的便“，反复执行这一步骤，直到没有圈为止。

试判断这种方法是否正确。若正确，说明理由，若不正确，举出反例（圈：就是回路）

答:正确。由于经过破圈法之后，最终没有回路，故一定可以构造出一颗生成树。

证明其是最小生成树：记“破圈法”生成的树为T，假设T不是最小生成树，则必然存在最小生成树T0，使得它与T的公共边尽可能的多，则将T0与T取并集，得到一个图，此图必然存在回路，“破圈法”从回路去除权最大的边，此时生成的T权必然最小，与原假设T不是最小生成树矛盾，从而T是最小生成树。

 

 06、试说明利用DFS如何实现有向无环图拓扑排序。

//用DFS实现有向无环图的拓扑排序

//思路：用time变量记录每个结点DFS的结束时机
//由于是拓扑排序 则输出结点在前的结点的time值一定大
//将每个结点的time值保存在一个数组中 最后按time值由大到小输出结点值 则是拓扑有序的
 
 bool visited[MAXVERTEXS]; 
void DFSTraverse(Grapg G)
{
	for(int v=0;i<G.vertex;v++)
		visited[v]=false;
	int time=0;
	for(int v=0;v<G.vexnum;v++)
		if(!visited[v])
			DFS(G,v);
	
}

void DFS(Graph G,int v)
{
	visited[v]=true;
	visit(v);
	for(w=FirstNeighbor(G,v),w>=0;W=NextNeighbor(G,v,w))
		if(!visited[w])
			DFS(G,w);
	time+=1;//退出递归时time增1 注意：这里着重理解 可手绘图来分析 
	FinishTime[v]=time;
}

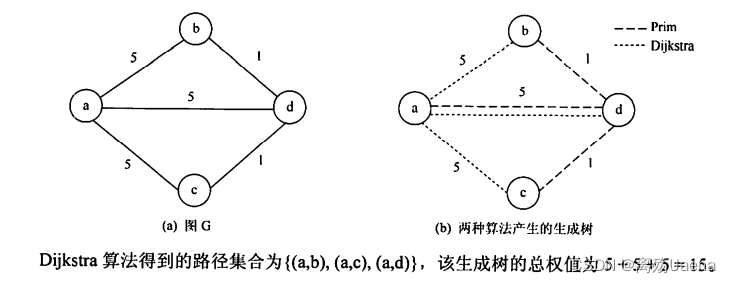
07、一连通无向图，边非负权值，文勇Dijkstra最短路径算法能否给出一颗生成树，该树是否一定是最小生成树？

Dijkstra算法可以产生一棵树 但不一定是最小生成树

如图：

 

10、

 

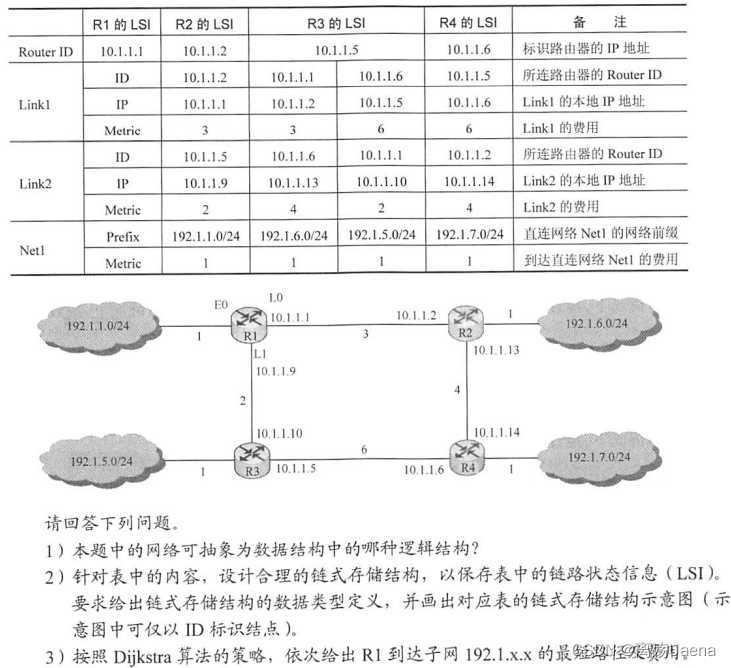
 答:

1):可以抽象为无向图

2):存储 结构如下图：

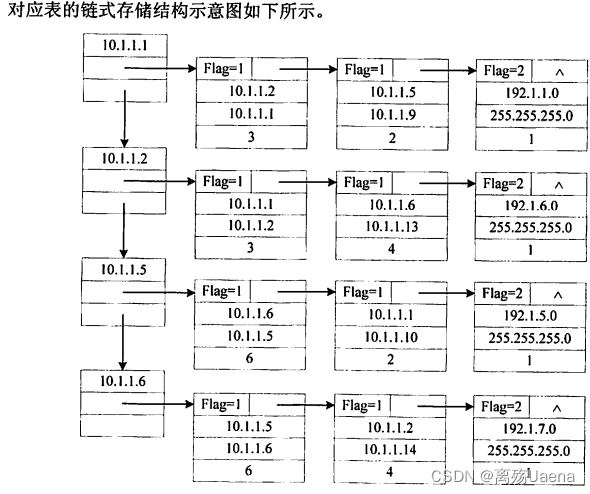
对应表的链式存储结构如下图：