今天开始正式进行高数的内容复习。
第一部分,函数极限,主要包括五块内容:函数的概念与特性、函数的图像、函数极限的概念和性质、计算、函数的连续性与间断
本文整理的是第一部分的前半部分,函数的概念与特性+函数的图像。
一、函数的概念与特性
(一)函数
设
与
是两个变量,
是一个给定的数集,若对于每一个
,按照一定的法则
,有一个确定的值与之对应,则称
为
的函数,记作
,称
为自变量,
为因变量,称数集
为此函数的定义域,定义域一般由实际背景中的变量的具体意义或者函数对应法则的要求确定,称
为值域。(每一个
值都最多对应一个
值)
(二)反函数
设函数
的定义域为
,值域为
,如果对于每一个
,必存在唯一的
使得
成立,则由此定义了一个新的函数
,这个函数称为函数
的反函数,一般记作
,它的定义域为
,值域为
,相对于反函数来说,原来的函数也称为直接函数。
严格单调函数必有反函数,有反函数的函数不一定是单调函数
若把
与
的图像画在同一坐标系中,它们完全重合。只有把反函数的
与
互换后,他们的图像才关于 对称,事实上这也是字母
与
互换的结果。(直接函数与反函数在同一个坐标轴中图像的各个点是一样的也就是说图像是完全重合的,但是实际上,他们的值域和定义域刚好相反,为了区别,将反函数的
与
互换,变成标准的
形式,这使得他们关于
对称
口诀:铅垂直线定单多,水平直线定反直。(铅垂直线与函数最多一个交点,那么该函数是单值函数(一般认为考研期间的函数默认都是单值函数,即符合函数的定义);水平直线与函数最多一个交点,那么该函数有反函数)。
(三)复合函数
设函数
的定义域为
,函数
在
上有定义,且
,则由
确定的函数称为由函数
和函数
构成 的复合函数,他的定义域为
,
称为中间变量。
(四)隐函数
设方程
,若当
取某区间内的任一值时,总有满足该方程的唯一的值
存在,则称方程
在上述区间内确定了一个隐函数
。
简单的说,就是相较于这种形式,更难以看出
与
之间关系的函数。比如
是显函数,而
是隐函数,显然它们实际上是同一个式子,这里的隐函数也可以转换为显函数,但是有些函数因为
与
关系较为复杂,只能用
的隐函数形式表示。
(五) 函数的四种特性
1、有界性
设
的定义域为
,数集
,如果存在某个正数
,使对任一
,有
,则称
在
上有界;如果这样的
不存在,则称
在
上无界。
例如, 存在和
,使
成立,则
有界。当然,讨论有界无界的前提是指定区间
。
2、单调性
设f的定义域为
,区间
,如果对于区间
上任意两点
,
,当
<
时,恒有
<
,则称在区间上单调增加。反之则是单调减少。
3、奇偶性
设
的定义域
关于原点对称(若
,则
),如果对于任一
,恒有
,则称
为偶函数,如果对于任一
,恒有
,则称
为奇函数。
偶函数的图像关于轴对称,奇函数的图像关于
轴对称。
4、周期性
设
的定义域为
,如果存在一个正数
,使得对于任一
,有
,且
,则称
为周期函数,
称为
的周期。
二、函数的图像
(一)基本初等函数与初等函数
基本初等函数包括:常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数
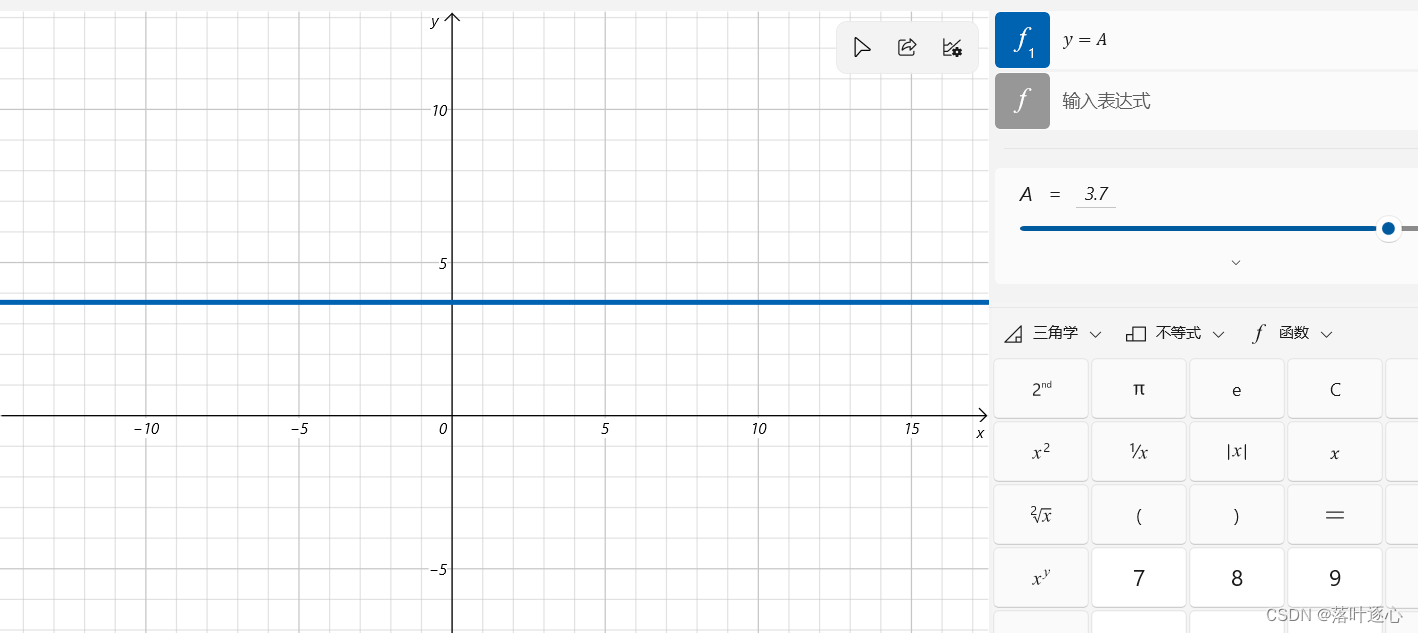
1、常数函数
,
为常数。(如图1.1)
其图像为平行于
轴的水平直线。
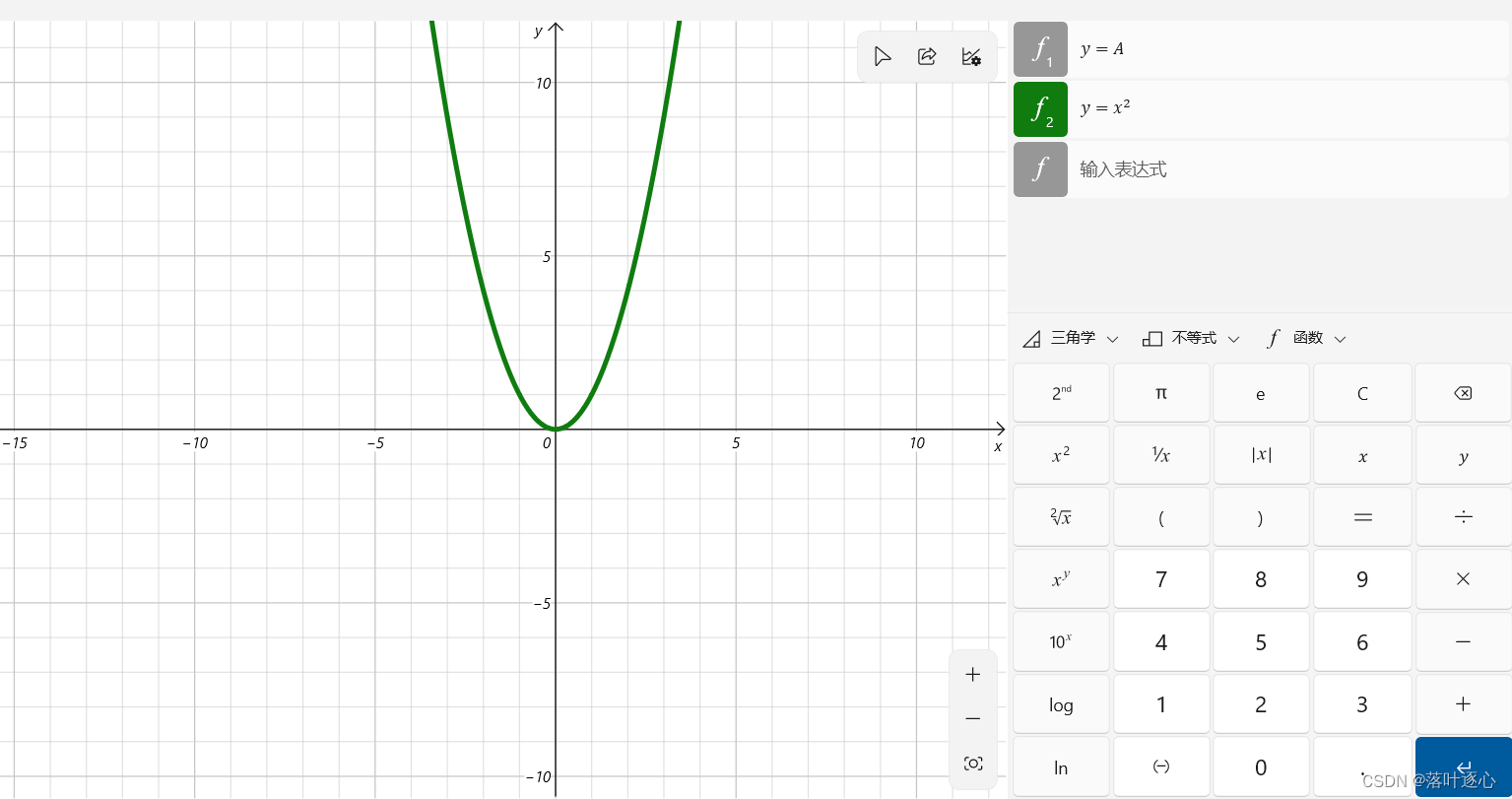
2、幂函数
(
是实数)。(如图1.2)
的定义域和值域取决于
的值,当
时,
都有定义。
当
时,
具有相同的单调性且与
具有相反的单调性。
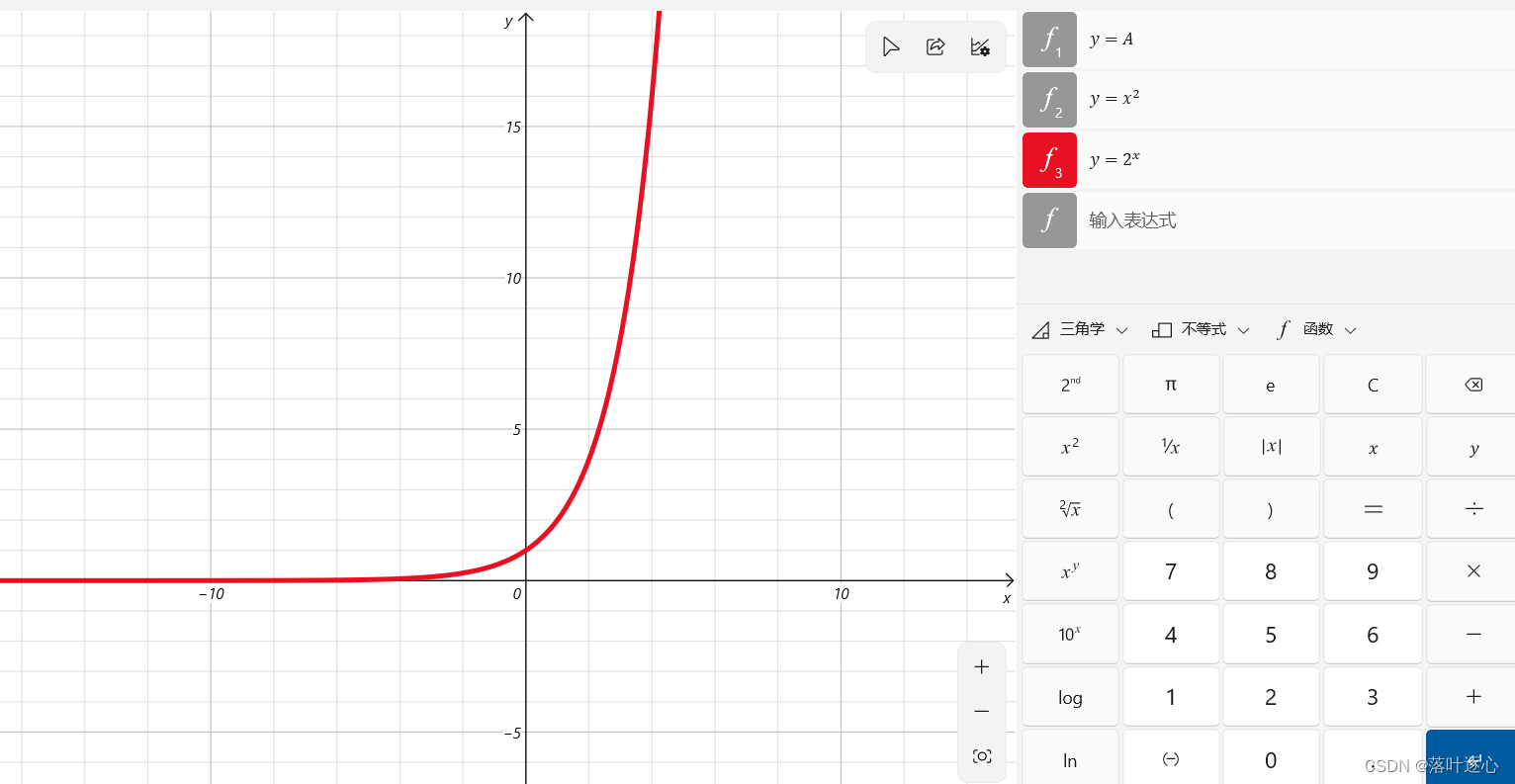
3、指数函数
。(如图1.3)
定义域:
,值域:
当
时,
单调增加;当
时,
单调减少。
常用指数函数:
(如图1.4)
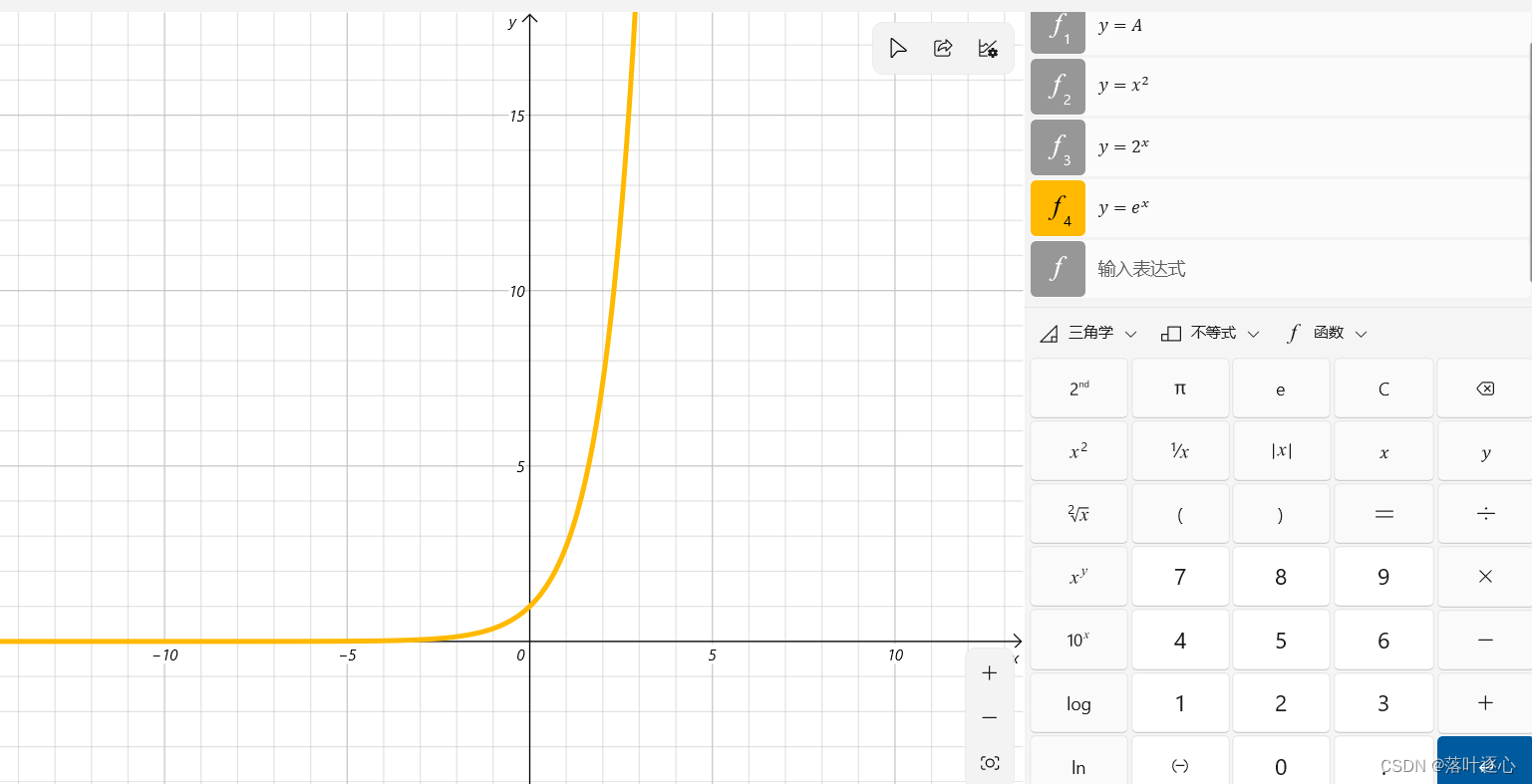
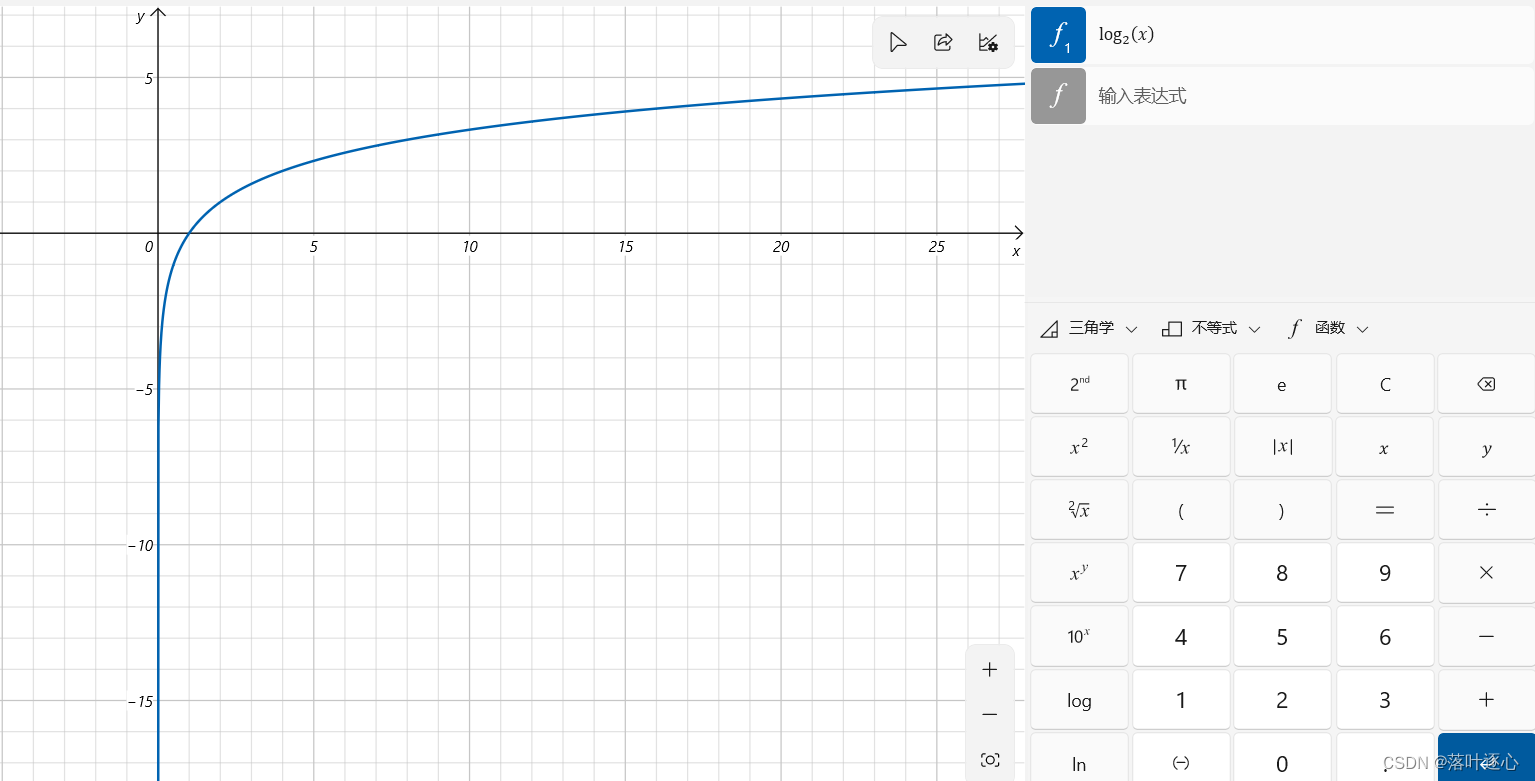
4、对数函数
。(如图1.5)
与
成反函数
定义域为:
,值域为:
当
时,
单调增加;当
时,
单调减少
常见特殊对数函数值:
,
,
5、三角函数
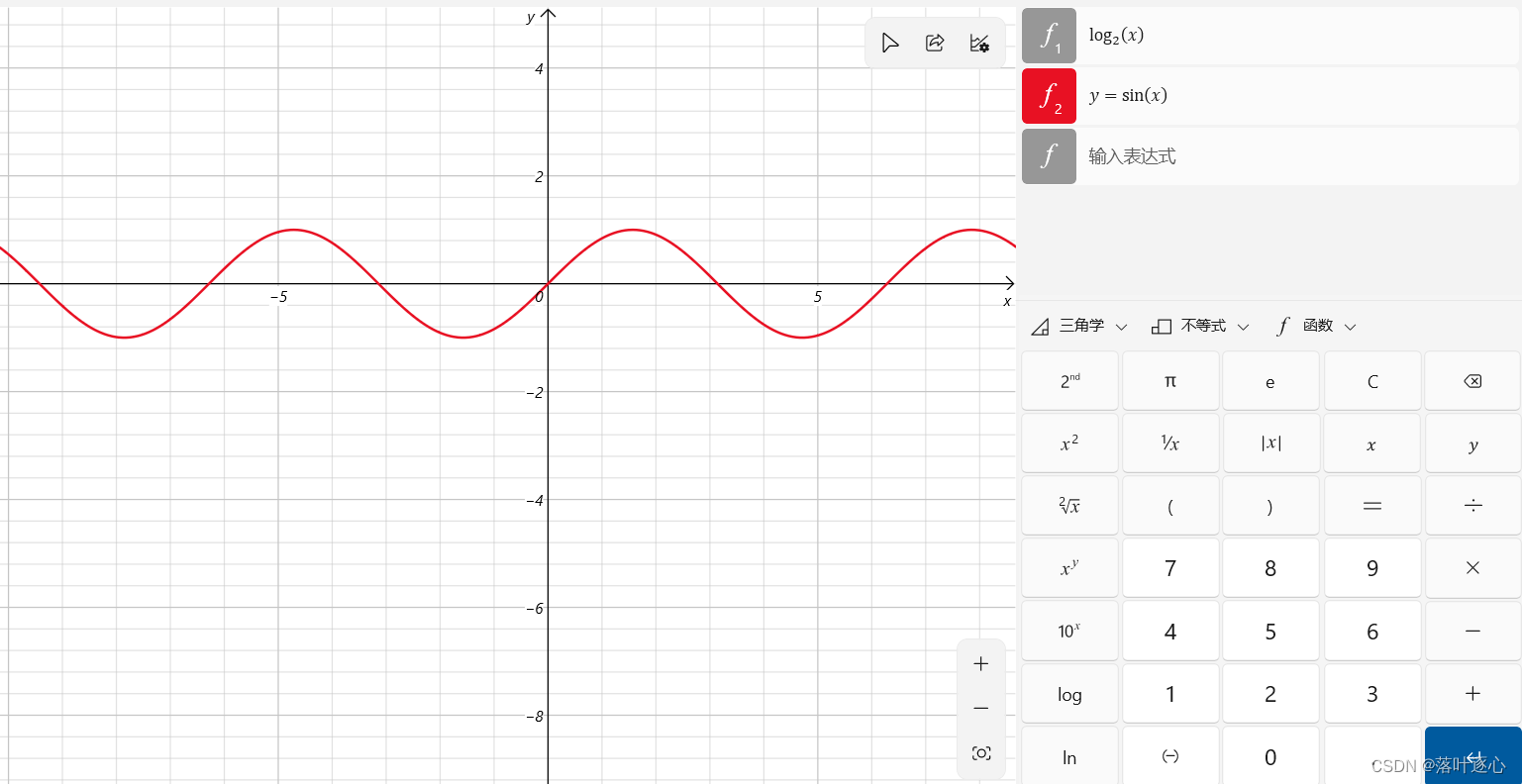
正弦函数:。(如图1.6)
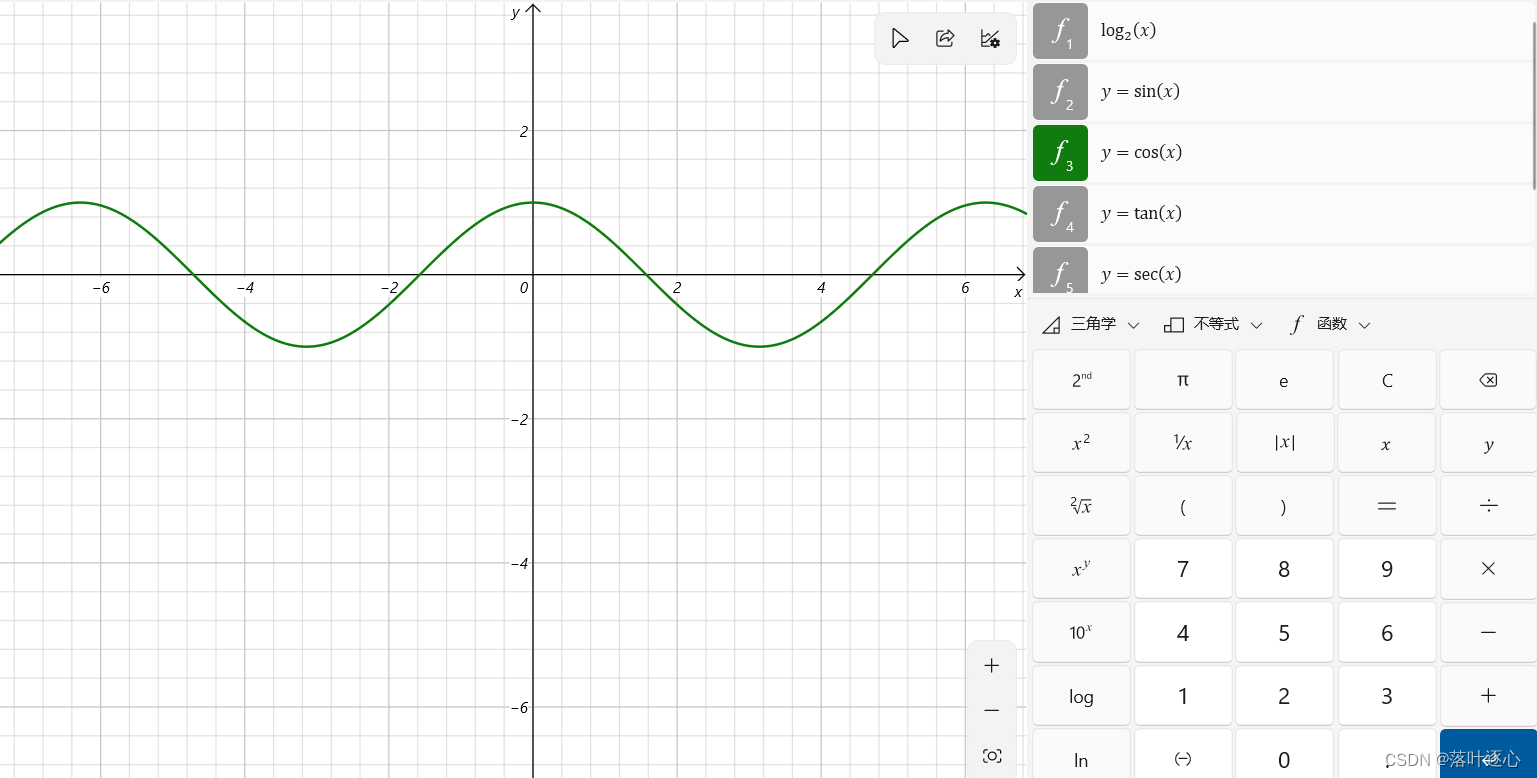
余弦函数:。(如图1.7)
定义域:
,值域:
正弦函数是奇函数,余弦函数是偶函数,
和
都是以
最小正周期的周期函数,
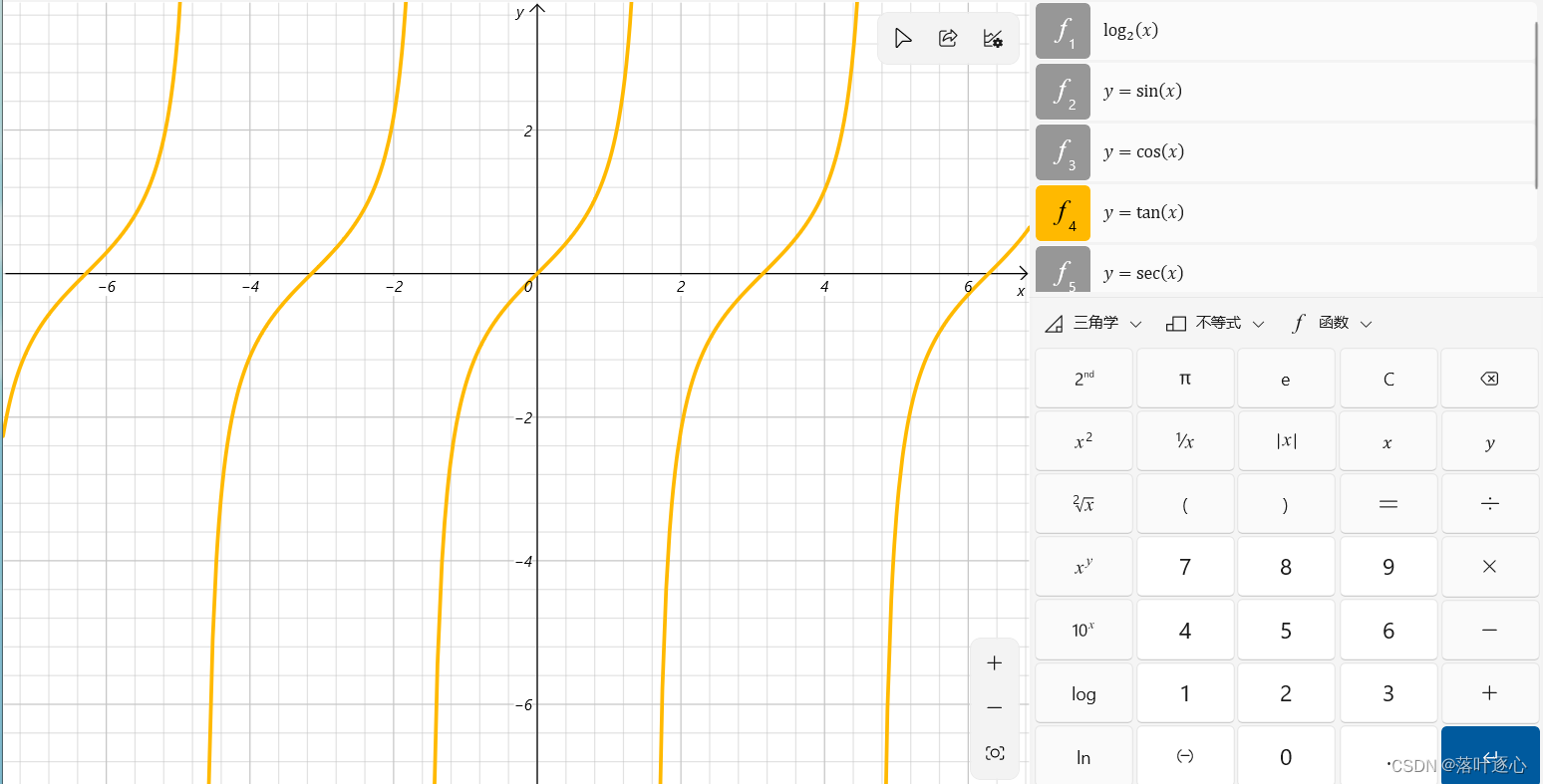
正切函数:。(如图1.8)
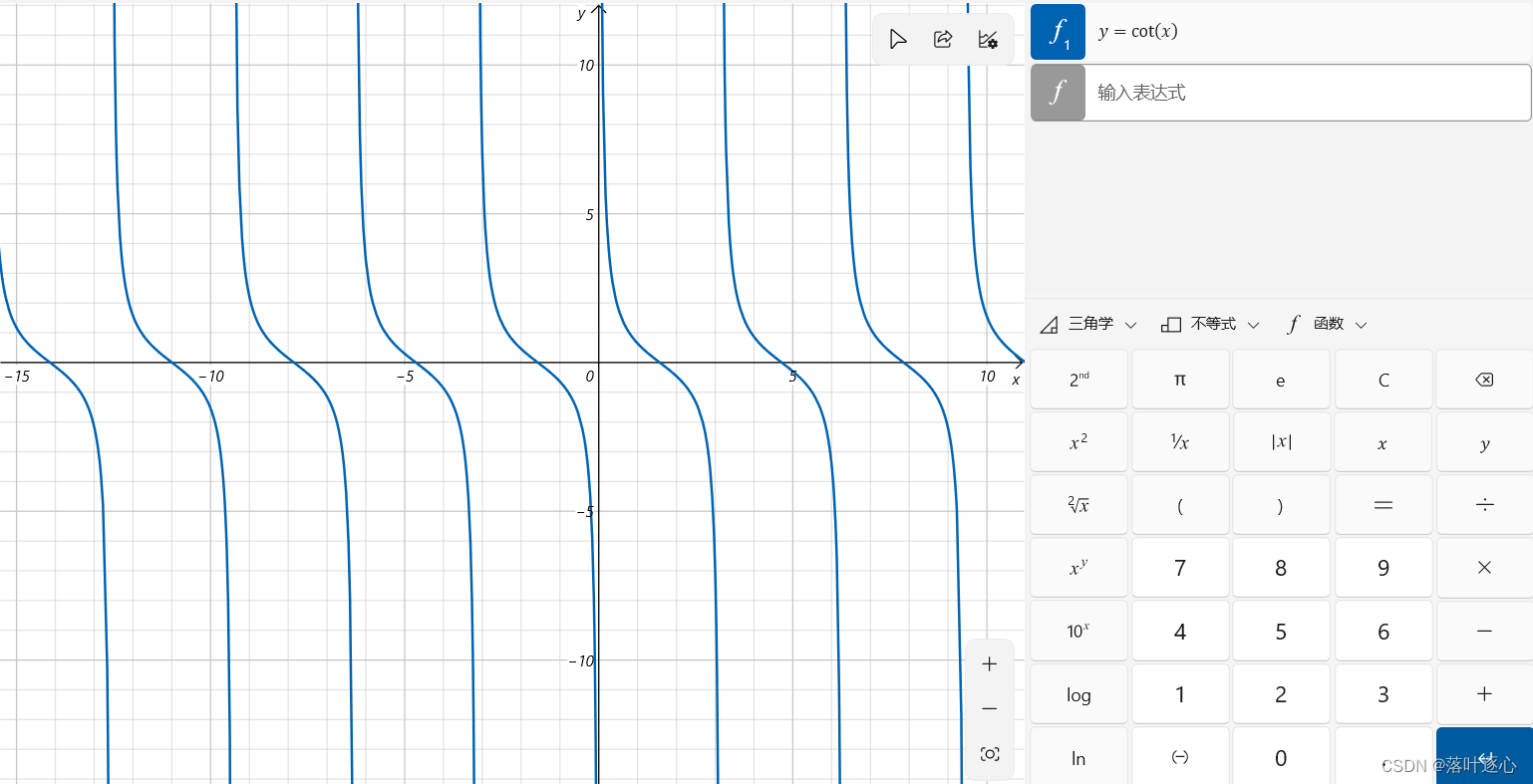
余切函数:。(如图1.9)
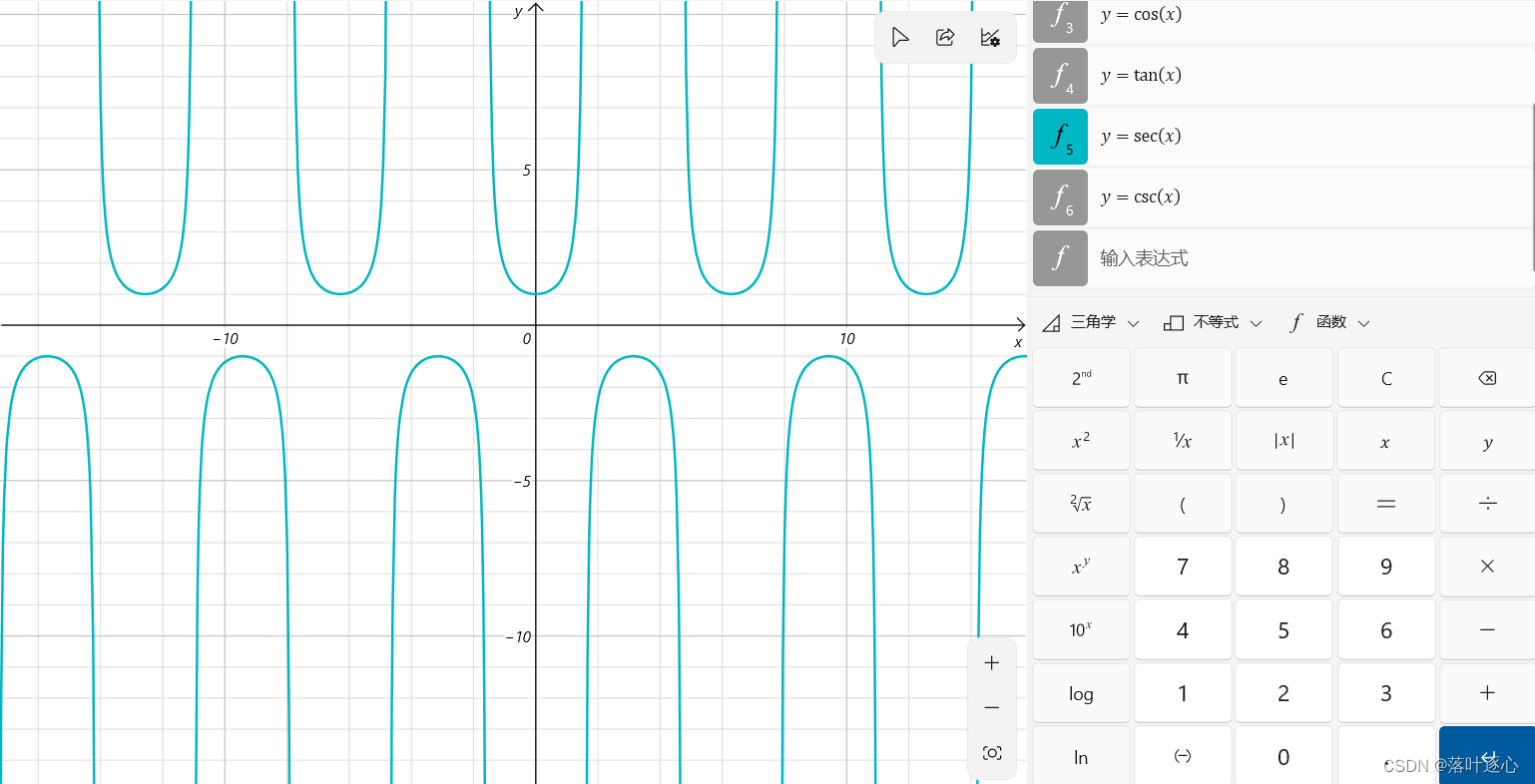
正割函数:。(如图2.0)
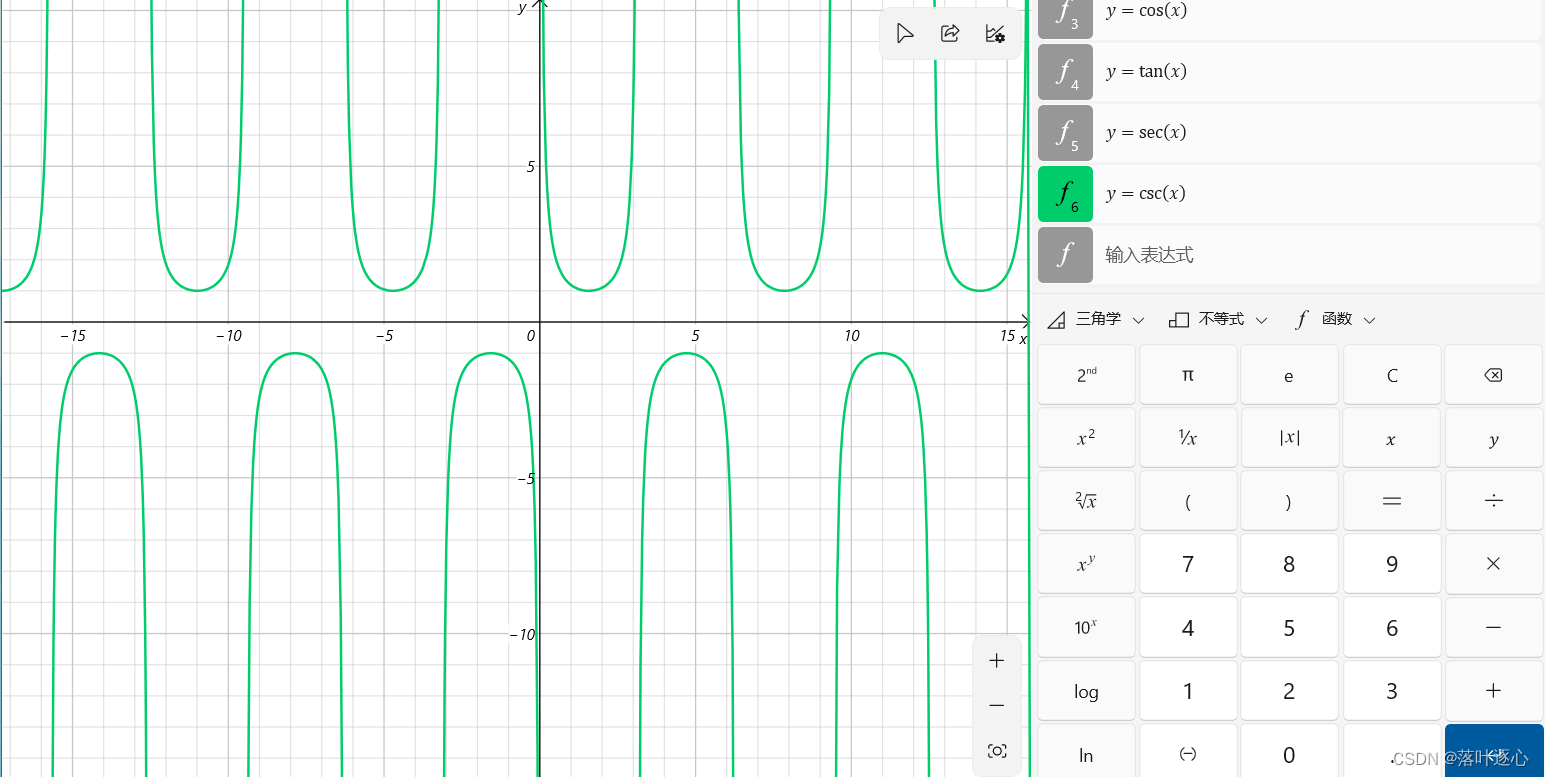
余割函数:。(如图2.1)
;
6、反三角函数
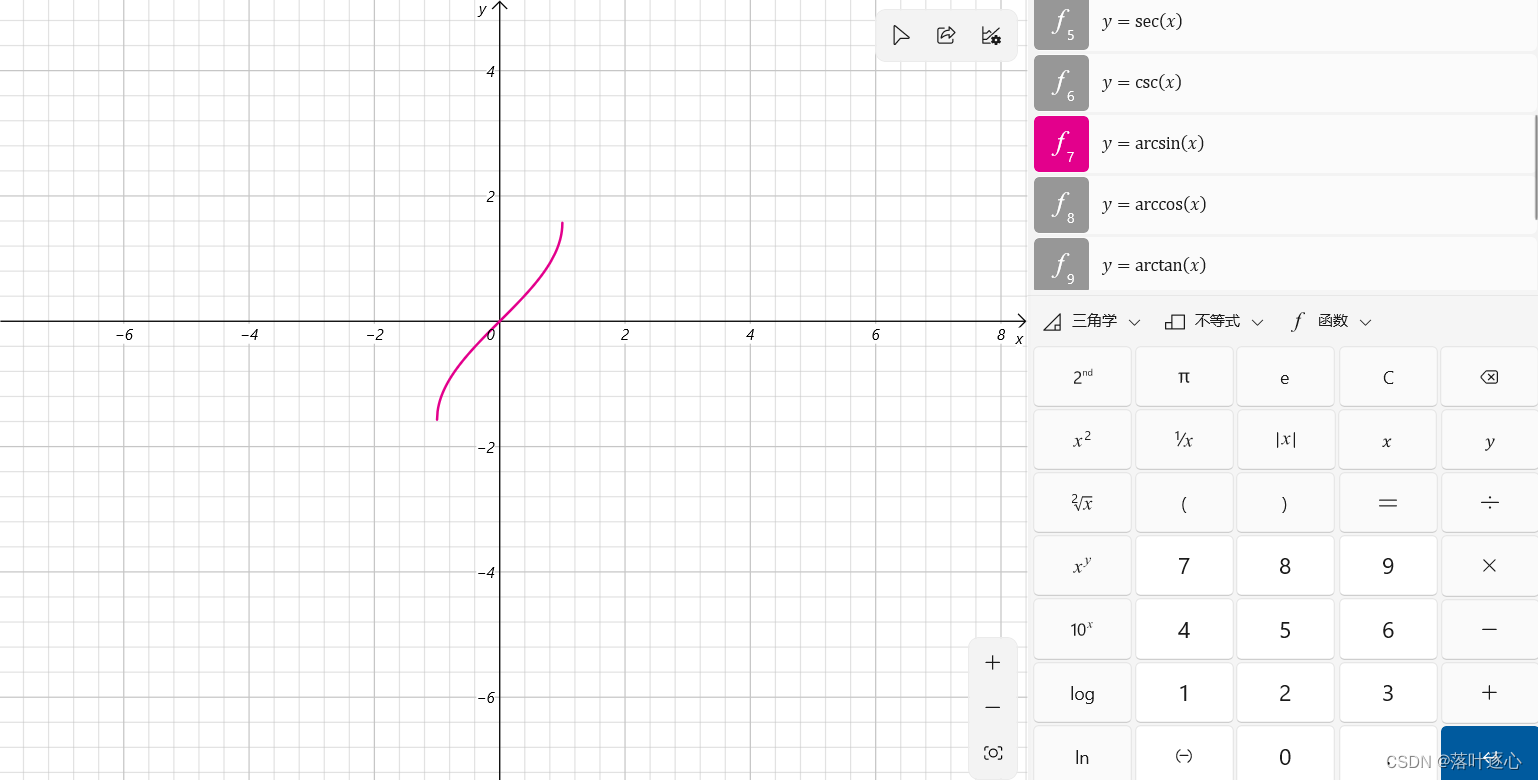
反正弦函数:(如图2.2)
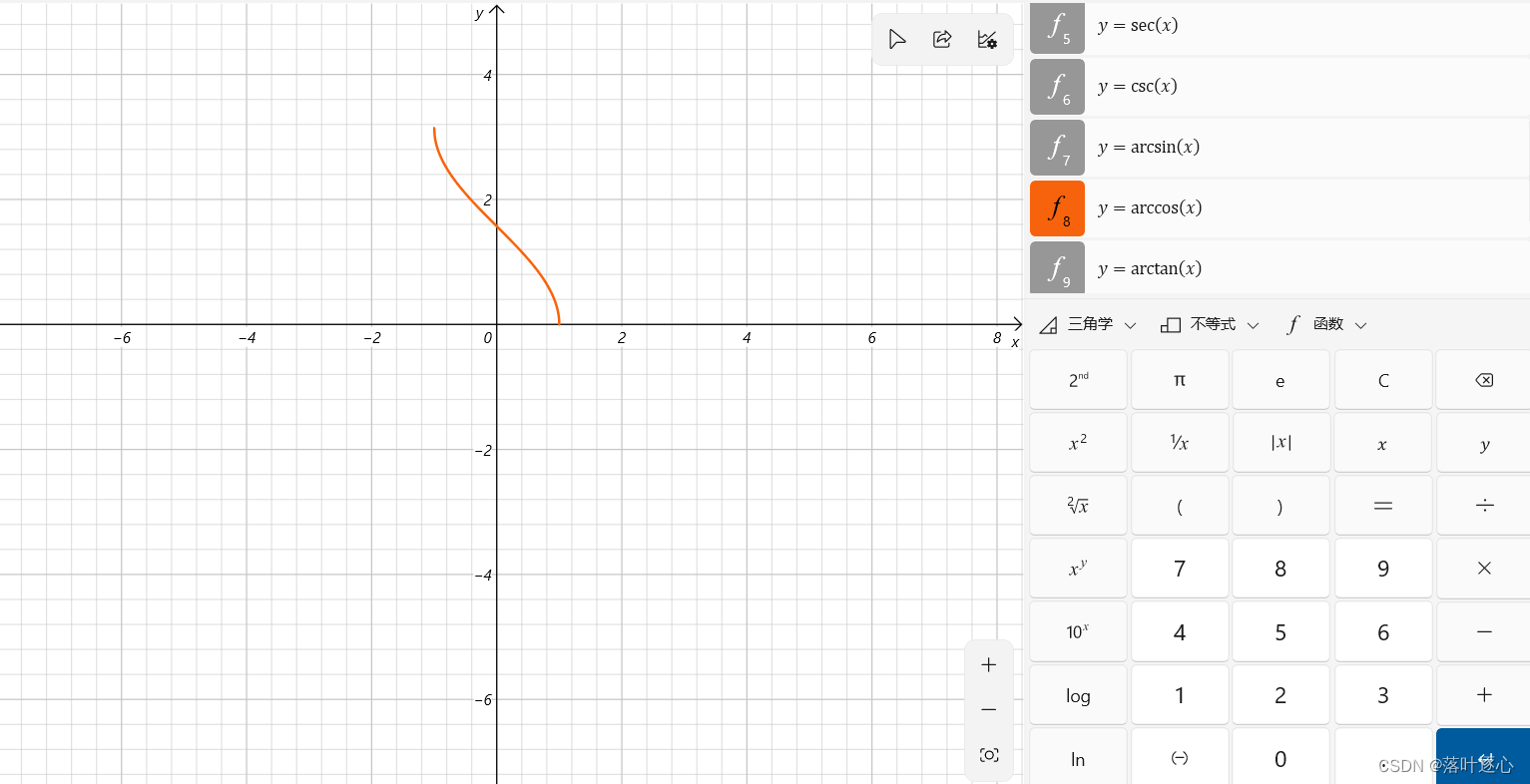
反余弦函数:(如图2.3)
是
的反函数,
是
的反函数
的主值区间为
,
的主值区间为
反三角函数的恒等式有:
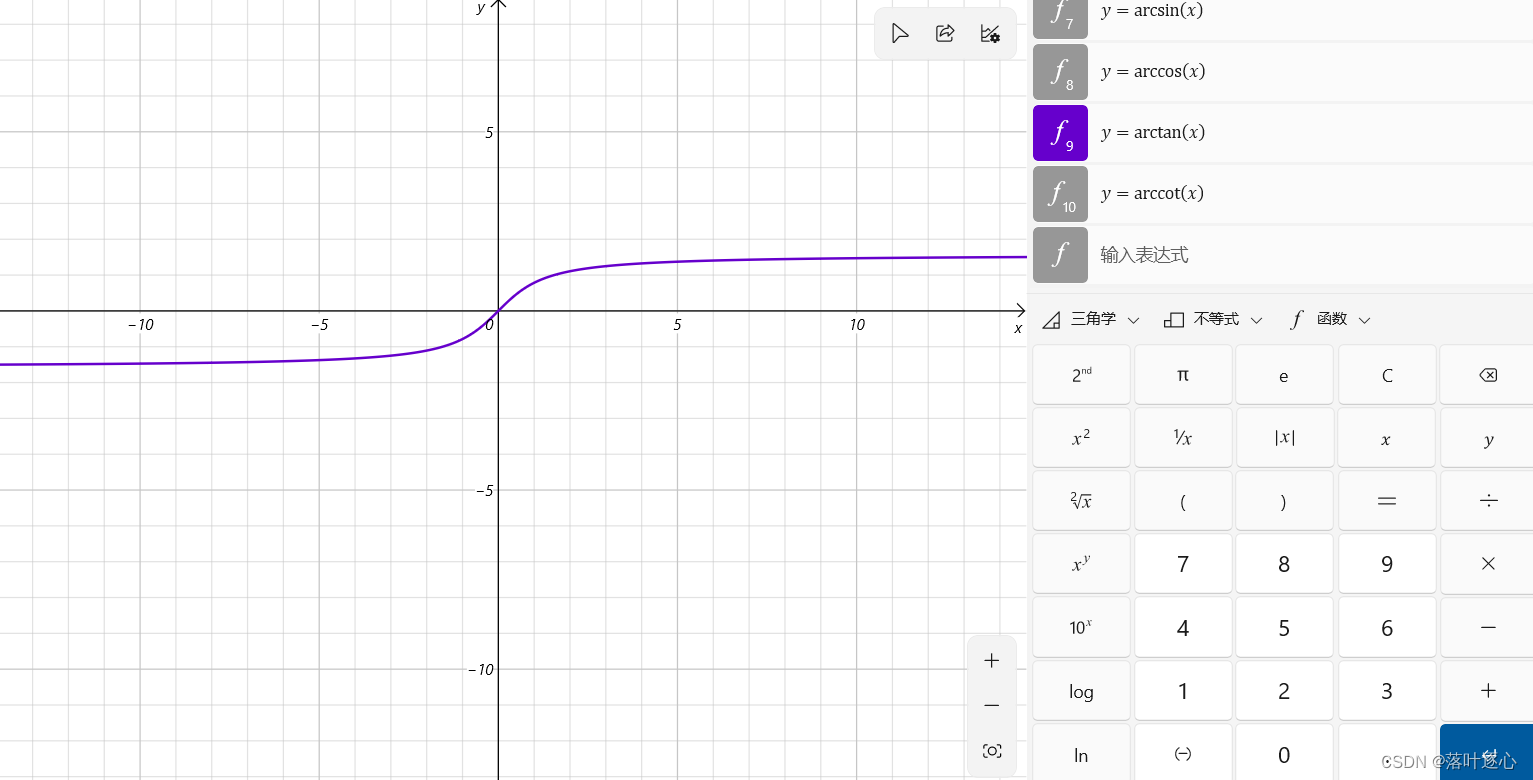
反正切函数:(如图2.4)
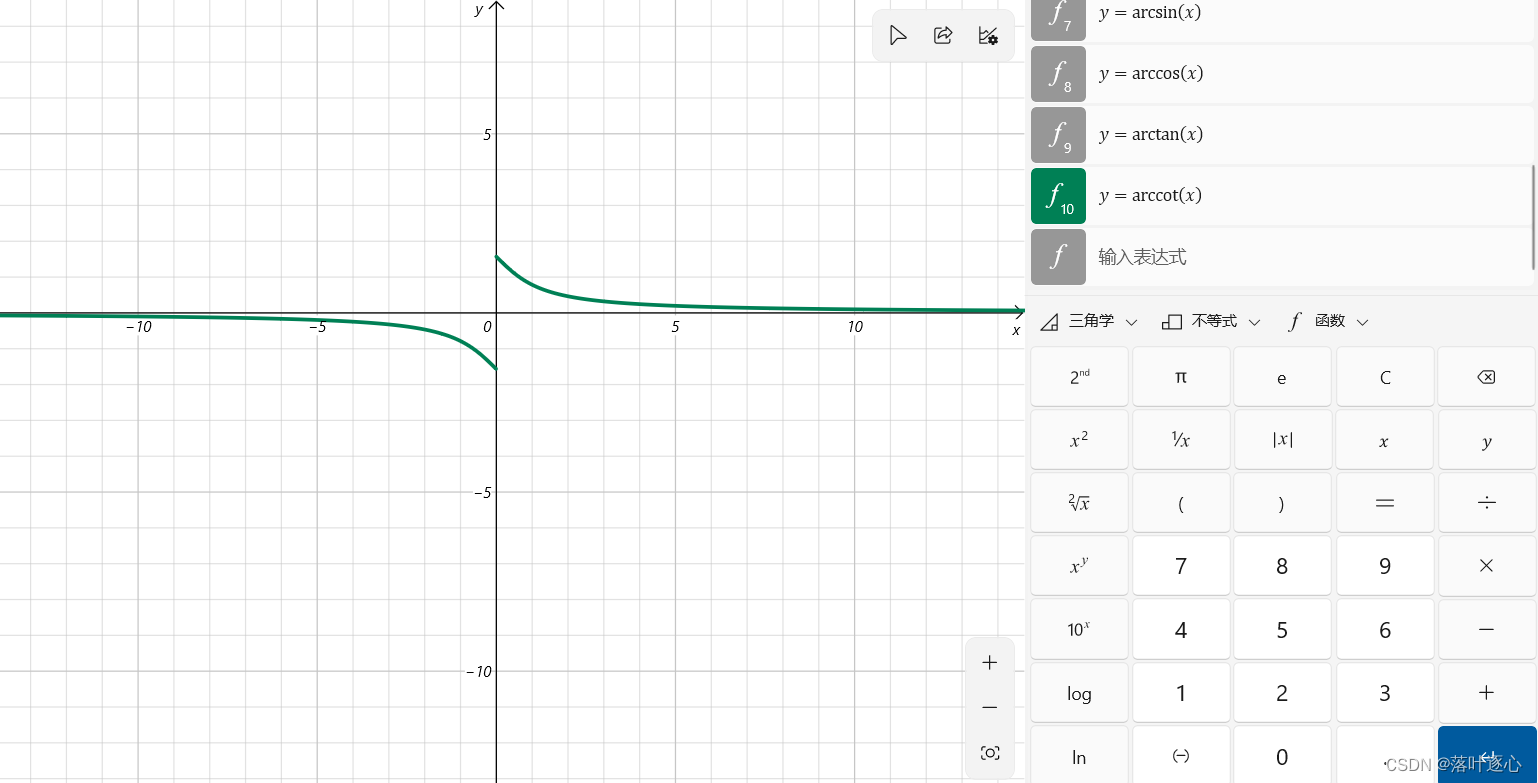
反余切函数:(如图2.5)
是
的反函数,
是
的反函数
反正余切函数的定义域为:
,
的值域为
,
的值域为
单调性:
单调增加,
单调减少
奇偶性:
为奇函数
7、初等函数
由基本初等函数经过有限次的四则运算,以及有限次的复合步骤所构成的并且可以由一个式子所表示的函数称为初等函数
初等函数的定义域可以是一个区间,也可以是几个区间的并集,甚至可以是一些孤立的点
(二)分段函数
在自变量的不同变化范围中,对应法则用不同的式子来表示的函数称为分段函数。分段函数是用几个式子来表示一个(不是几个)函数,它不是初等函数。其典型形式如下:









 本文介绍了数学中的函数极限理论,特别是第一部分:函数的概念与特性、函数图像,涵盖了函数定义、反函数、复合函数、隐函数及其特性,以及基本初等函数如指数、对数和三角函数的图像分析。同时提及了分段函数的概念。
本文介绍了数学中的函数极限理论,特别是第一部分:函数的概念与特性、函数图像,涵盖了函数定义、反函数、复合函数、隐函数及其特性,以及基本初等函数如指数、对数和三角函数的图像分析。同时提及了分段函数的概念。














 560
560











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








