前言
最短路径问题是图论研究中的一个经典算法问题，图中从一个顶点到达另一个顶点的路径可能不止一条，最短路径问题旨在寻找图（由结点和路径组成的）中两结点之间的最短路径。本文讨论两种常见的最短路径问题--单源最短路径问题和多源最短路径问题。
一、单源最短路径
单源最短路径是指从从一个固定的起始点出发到其余所有点的路径。在单源最短路径中，根据是否存在负权边对相应的算法进行了更为细致的分类。
1.1权值均为正的单源最短路径
给定一个带权有向图 D 与源点 v ，求从v 到 D 中其它顶点的最短路径。限定各边上的权值大于0。
如何求得这些路径？迪杰斯特拉(Dijkstra)提出了一个按路径长度递增的次序产生最短路径的算法。首先求出长度最短的一条最短路径，再参照它求出长度次短的一条最短路径，依次类推，直到从顶点 v 到其它各顶点的最短路径全部求出为止。
解决步骤描述：
1. 设置辅助数组dist。它的每一个分量dist[i]表示当前找到的从源点 v0到终点 vi的最短路径的长度；
2. 初始状态：
2.1. 若从源点 v1 到顶点 vi有边：dist[i]为该边上的权值；
2.2. 若从源点 v1到顶点 vi无边：dist[i]为∞。
根据以上描述，可以得到如下描述的算法：
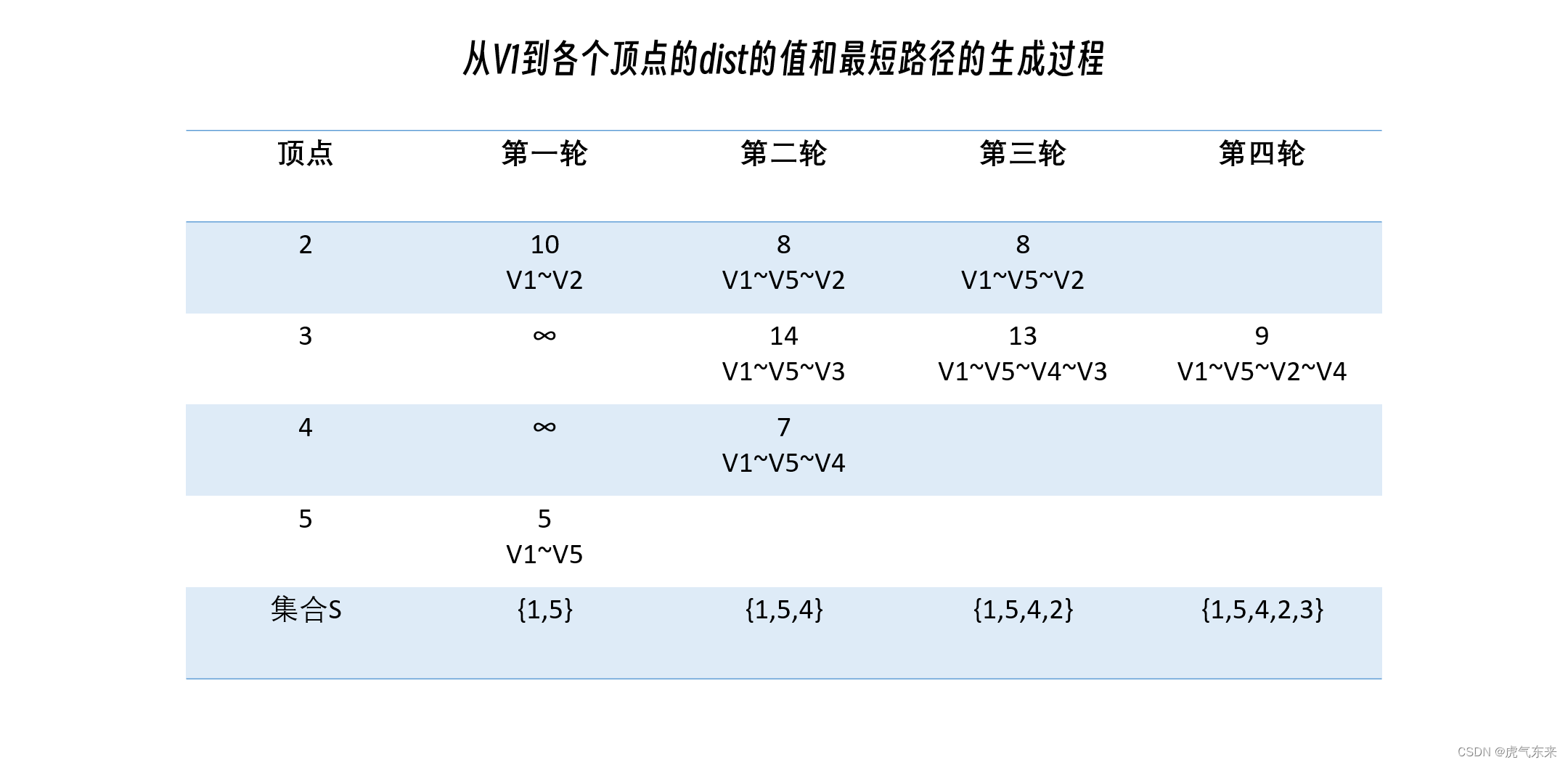
1，将集合S初始化为{V1}，易知dist[2]=10,dist[3]=∞，dist[4]=∞，dist[5]=5。则第一轮选出的最小的dist[5]，将5放入集合S
2，因为有了顶点5的加入，需要更新dist数组。易知idst[2]=8,dist[3]=14,dist[4]=7;则在第二轮选出最小的dist[4],将4放入集合S
3，依此类推......直到全部的顶点包含在集合S中。
代码示例：
void Dijkstra(int sv) //起点sv
{
int i = 0;
int j = 0;
// 合法性判断
if( (0 <= sv) && (sv < VNUM) ) //VNUM顶点个数
{
// 初始化辅助数组
for(i=0; i<VNUM; i++)
{
Dist[i] = Matrix[sv][i];
P[i] = sv; // 最短路径的顶点的上一个顶点
Mark[i] = 0;
}
// 标记顶点sv，即初始化集合S
Mark[sv] = 1;
// 循环求得sv到某个顶点的最短路径
for(i=0; i<VNUM; i++)
{
int min = MV; // 当前离sv顶点最短路径
int index = -1; // 下个最短路径的顶点
// 遍历其余未被标记的顶点，找到最短路径及最短路径的顶点
for(j=0; j<VNUM; j++)
{
if( !Mark[j] && (Dist[j] < min) )
{
min = Dist[j];
index = j;
}
}
// 标记找到的最短路径的顶点，放入集合S中
if( index > -1 )
{
Mark[index] = 1;
}
// 更新当前最短路径及顶点
for(j=0; j<VNUM; j++)
{
// 修改：dist[i] ← min{ dist[i], dist[k] + Edge[k][i],i ∈ V- S
if( !Mark[j] && (min + Matrix[index][j] < Dist[j]) )
{
Dist[j] = min + Matrix[index][j];
P[j] = index;
}
}
}
// 打印最短路径及顶点
for(i=0; i<VNUM; i++)
{
int p = i;
// 顶点sv到其它顶点的路径
printf("%d -> %d: %d\n", sv, p, Dist[p]);
// 最短路径顶点关系
do
{
printf("%d <- ", p);
p = P[p];
} while( p != sv );
printf("%d\n", p);
}
}
1.2权值有负的单源最短路径
当一张图中存在负权边时，Dijstra算法就无法算出正确的解，这个时候我们要用到Bellman-Ford算法[6]。但是，需要注意：1，当这张图存在负权环时是无法算出最短路径的，不过也可以用Bellman-Ford算法判断这张图是否有负权环。2，Bellman-Ford算法一般处理的是有向图，因为如果是无向图，那么如果存在一条负权边，就会构成负权环了。
算法原理：
如果一个图没有负权环，那么从一点到另一个点的最短路径最多经过所有的V个顶点，经过V-1条边。对一个点的一次松弛操作，就是找到经过这个点到与其相邻的点的另外一条路径，多一条边，而权值更小。或者可以理解为：每次加入新的节点i，将节点i作为中间节点，判断源点—>节点i—>各个节点的最短距离 较之于 上一次的最短距离是否会有更新。那么我们只要对所有的点进行V-1次松弛操作，就可以求出从起点开始对任意一点的距离。如果还可以进行松弛操作，那么说明这个图有负权环(如果有负权环，则可以进行无数次松弛操作)。
(虽然说是对i点进行松弛操作，但实际上是对i直接相邻的点进行改变的)
例如：求1号结点到所有结点之间的距离[7]。
首先初始化数据结构，将dist数组的第0位置空(可以不用考虑)，因为初始化数组dis的时候默认为顶点1还没有边相连，所以设置顶点1到其余各个顶点的距离均为∞。右表表示前一节点u，v,及其之间的权重w。
对第一轮的所有边进行松弛。
松弛后的结果为：
由于这个案例比较特殊，只进行了一次就已经将所有的路径都更新完毕了。但是更一般的情况，仍需要继续松弛，整个松弛过程需要进行V-1次。
代码实现：
#include <vector>
#include <iostream>
using namespace std;
class Bellman_Ford
{
private:
int vertice = 0;//顶点数
int edge = 0;//边数
vector<int> u;
vector<int> v;
vector<int> w;
vector<int> dis;//源点到各个顶点之间的最短距离
public:
//根据节点值和边值初始化：边的起始节点数组u，边的终止节点数组v，边u[i]->v[i]的权重w
Bellman_Ford(int x, int y) :vertice(x), edge(y)
{
//图的初始化从下标1开始
dis.resize(vertice + 1);
u.resize(edge + 1);
v.resize(edge + 1);
w.resize(edge + 1);
}
//检测负权回路
bool Detect_negative_weight_circuit()
{
bool flag = false;
for (int i = 1; i <= edge; i++)
{
if (dis[v[i]] > dis[u[i]] + w[i])
{
flag = 1;
}
}
return flag;
}
//读入图的边，并且根据边的信息初始化数组dis，数组book
void GetEdgeInfo()
{
cout << "输入边的信息（节点1，节点2，权重）：" << endl;
int e1 = 0, e2 = 0, weigth = 0;
for (int i = 1; i <= edge; i++)
{
cin >> e1 >> e2 >> weigth;
u[i] = e1;
v[i] = e2;
w[i] = weigth;
}
for (int i = 2; i <= vertice; i++)
{
//dis[1]在构造函数里面已经初始化为0
dis[i] = INT_MAX;
}
}
//打印
void Print()
{
for (int i = 1; i <= vertice; i++)
{
cout << dis[i] << " ";
}
cout << endl;
}
//Bellman_Ford核心思想
void Bellman_Ford_Alg()
{
for (int k = 1; k < vertice; k++)//控制松弛的轮数
{
bool check = false;//标记在本轮松弛中数组dis是否会发送更新
//找离1号节点最近的节点（找数组dis中的最小值）
for (int i = 1; i <= edge; i++)
{
if (dis[u[i]] < INT_MAX && dis[v[i]] > (dis[u[i]] + w[i]))
{
dis[v[i]] = (dis[u[i]] + w[i]);
check = true;//如果数组dis发生变化，check的值就改变
}
}
//松弛结束后判断dis数组是否发生变化
if (check == false)
{
break;
}
}
}
};
int main()
{
Bellman_Ford Bellman(5, 5);
Bellman.GetEdgeInfo();
cout << "初始信息：" << endl;
Bellman.Print();
Bellman.Bellman_Ford_Alg();
cout << "单源最短路径(顶点1到其余各顶点)：" << endl;
Bellman.Print();
bool tag = Bellman.Detect_negative_weight_circuit();
if (tag)
{
cout << "存在负权回路" << endl;
}
else
{
cout << "不存在负权回路" << endl;
}
return 0;
}
二、多源最短路径
多源最短路径是任意两顶点之间的路径。对于多源最短路径，最经典的就是Floyd算法。Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，需要不断地松弛。
现在有这样一张图，每个点只知道与其直接相连的点的距离，将图中的信息填入邻接矩阵。并且将邻接矩阵用二维数组dist[][]存储起来。
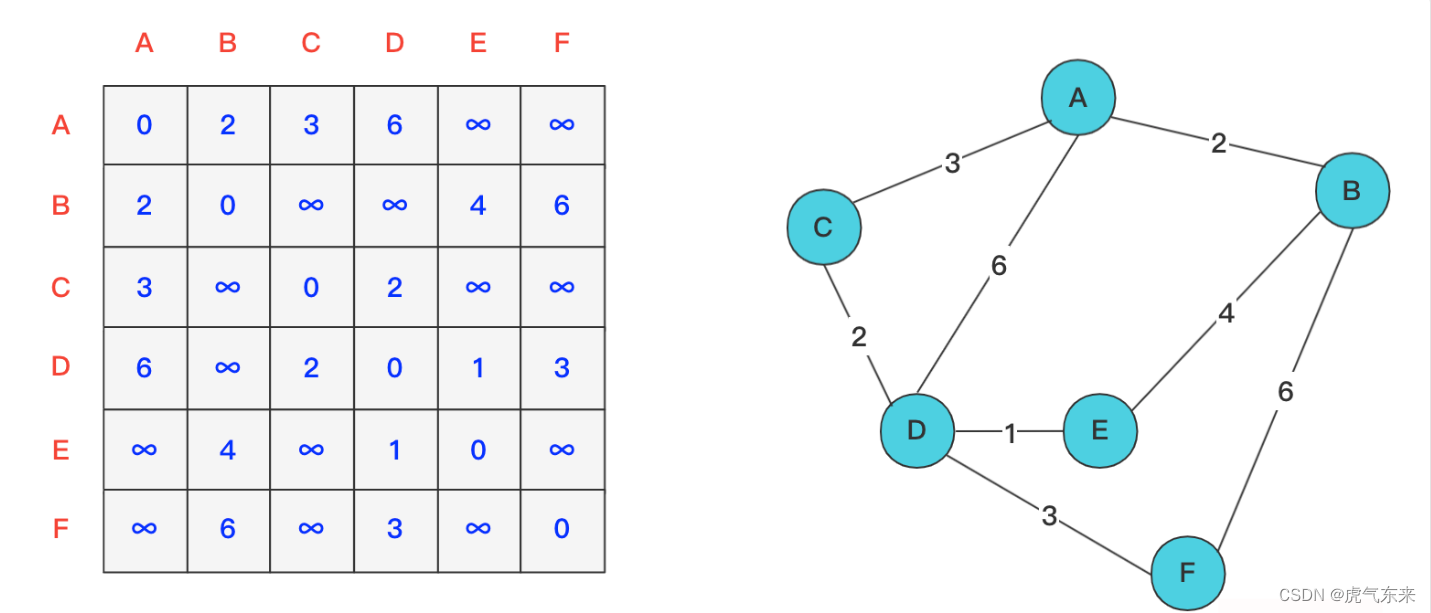
加入第一个节点A进行更新计算,大家可以发现，由于A的加入，使得本来不连通的B，C点对和B，D点对变得联通，并且加入A后距离为当前最小,同时你可以发现加入A其中也使得C-D多一条联通路径（6+3），但是C-D联通的话距离为9远远大于本来的(C,D)联通路径2，所以这条不进行更新[8]。
加入第二个节点B
代码演示：
参考文献
1，严蔚敏、吴伟民：《数据结构（C语言版）》
3， 数据结构之图的最短路径_顾小豆的博客-CSDN博客_数据结构最短路径
4，数据结构：图(Graph)【详解】_UniqueUnit的博客-CSDN博客_数据结构graph
最短路径_百度百科 (baidu.com)
7， Bellman-Ford解决单源最短路径（负权边）_阿宁(xin)。的博客-CSDN博客_单源最短路径 负边8,(建议收藏)一文多图，彻底搞懂Floyd算法(多源最短路径)_Big sai的博客-CSDN博客_多源最短路径
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
