【数字图像处理】图像增强

图像增强——频率域分析

卷积定理

函数卷积的傅里叶变换是函数傅里叶变换的乘积，即：一个域中的卷积相当于另一个域中的乘积

F(x)为傅里叶变换

傅里叶

傅里叶级数：任何周期函数都可以用不同频率的正弦函数和余弦函数构成的无穷级数来表示。

正弦波就是一个圆周运动在一条直线上的投影

使用正余弦波理论上可以叠加为一个矩形

参数：频率、振幅、相位

信号的两个观察面：

【1】时域：信号强度随时间的变化

【2】频域：信号是由哪些单一频率的信号合成的

傅里叶变换

计算机只处理离散的和有限长度的数据，因此使用DFT

离散傅里叶变换

1：傅里叶变换复数表示

欧拉公式：

复数：

2：一维离散傅里叶变换与反变换

输入信号f(x,y)

频率域F(u,v)

过滤元素：

3：二维离散傅里叶变换谱图

直流分量系数

将角上的4个DC 分量至于中心

DFT居中谱图

4：总结

【1】傅里叶变换将信号分成不同频率成份。

【2】傅里叶变换的成份：直流分量和交流分量

【3】信号变化的快慢与频率域的频率有关

频域图像分析基础

图像为什么要做频域变换？

【1】在频率域下，人眼对高频信息不敏感

【2】图像经过变换后，主要的信息集中在低频部分，保留低频分量就得到了图像在频域的稀疏表示

1个频率系数，其余设置为0，则仅保留直流分量系数。

        F(0,0) 称为频率谱的直流分量

        其它F(u,v) 值称为交流分量

        原点(0,0) 傅里叶变换是图像的平均灰度

噪声、边缘、跳跃部分代表图像的高频分量

背景区域和慢变部分代表图像的低频分量

傅里叶变换的频率分量(u,v)和图像空间特征（灰度变化模式）之间的联系：

【1】变化最慢的频率 (u=v=0)对应一幅图像的平均灰度级

【2】当从变换的原点移开时，低频对应着图像的慢变化分量，如图像的平滑部分

【3】进一步离开原点时，较高的频率对应图像中变化越来越快的灰度级，如边缘或噪声等尖锐部分

二维离散傅里叶变换的性质

【1】线性性

【2】可分离性

【3】平移性

【4】周期性、共轭对称和旋转不变性

图像频域滤波

1：空域卷积和DFT

2：频域卷积和傅里叶反变换

空间域滤波和频域滤波的关系

空间域和频域的滤波器构成傅里叶变换对

频率域滤波的基本步骤：通过滤波器函数以某种方式来修改图像变换，然后通过取结果的反变换来获得处理后的输出图像

常见滤波器

1：低通滤波器

使低频通过，高频衰减的滤波器

被低通滤波的图像比原始图像少了尖锐的细节部分而突出了平滑过渡部分

低通滤波结果：模糊

2：高通滤波器

使高频通过而使低频衰减的滤波器

被高通滤波的图像比原始图像少了灰度级的平滑过渡而突出了边缘等细节部分

高通滤波结果：锐化

频域滤波实现步骤

1：滤波步骤

2：空域填充

3：中心化（频谱）

4：傅里叶变换

5：设计滤波器

6：对位相乘

7：傅里叶逆变换

8：空域取消填充

低通滤波器

平滑/钝化可以通过衰减高频分量的范围来实现

1：频域低通滤波基本思想

2：理想低通滤波器（ILPF，ideal low pass filter）

转换函数满足分段函数，截断傅里叶变换中的所有高频成分，这些高频成分处于指定距离D0之外

ILPF截至频率设计：

【1】中心平移，以频域中心为原点求出总的信号能量

【2】以r为半径的圆就包含了百分之β 的能量，u,v是以D0为半径的圆所包括的全部u和v

【3】求出相应的D0

半径D0越小，模糊越大；半径D0越大，模糊越小

被钝化的图像被一种非常严重的振铃干扰，即：图像边缘有抖动或模糊的现象

ILPF的特点：

【1】严格控制低频和高频之间截止频率的过渡

【2】可能产生振铃

3：Butterworth低通滤波器（BLPF）

变换函数在通带与被滤除的频率之间没有明显的截断

半径D0越小，模糊越大；半径D0越大，模糊越小

BLPF的特点：

【1】变换函数中不存在一个不连续点作为一个通过的和被滤波掉的截止频率的明显划分

【2】通常把H(u,v)开始小于其最大值的一定比例的点当作其截止频率点

【3】在任何经BLPF处理过的图像中都没有明显的振铃效果，是滤波器在低频和高频之间的平滑过渡的结果

【4】BLPF低通滤波是一个以牺牲图像清晰度为代价来减少干扰效果的修饰过程

4：高斯低通滤波器（GLPF）

半径D0越小，模糊越大；半径D0越大，模糊越小

GLPF的特点：

【1】GLPF不能达到有相同截止频率的二阶BLPF平滑效果

【2】GLPF没有振铃

高通滤波器

1：频域高通滤波基本思想

2：理想高通滤波器（IHPF）

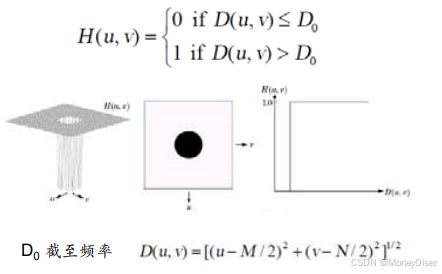
振铃问题

3：Butterworth高通滤波器（BHPF）

特点：

【1】变换函数中不存在一个不连续点作为一个通过的和被滤波掉的截止频率的明显划分

【2】通常把H(u,v)开始小于其最大值的一定比例的点当作其截止频率点

【3】低频成分被严重消弱，使图像失去层次

【4】为了解决变暗的趋势，在变换结果图像上再进行一次直方图均衡化。这种方法被称为后滤波处理

4：高斯高通滤波器（GHPF）

同态滤波器

1：同态滤波基本思想

思想：对图像灰度范围进行调整，通过消除图像上照明不均的问题，增强暗区的图像细节，同时又 不损失亮区的图像细节

照明函数i(x,y)

反射函数r(x,y)

目的：压缩低频成分，扩展高频成分

2：同态滤波定义

处理过程：

3：同态滤波实现