第六章 图
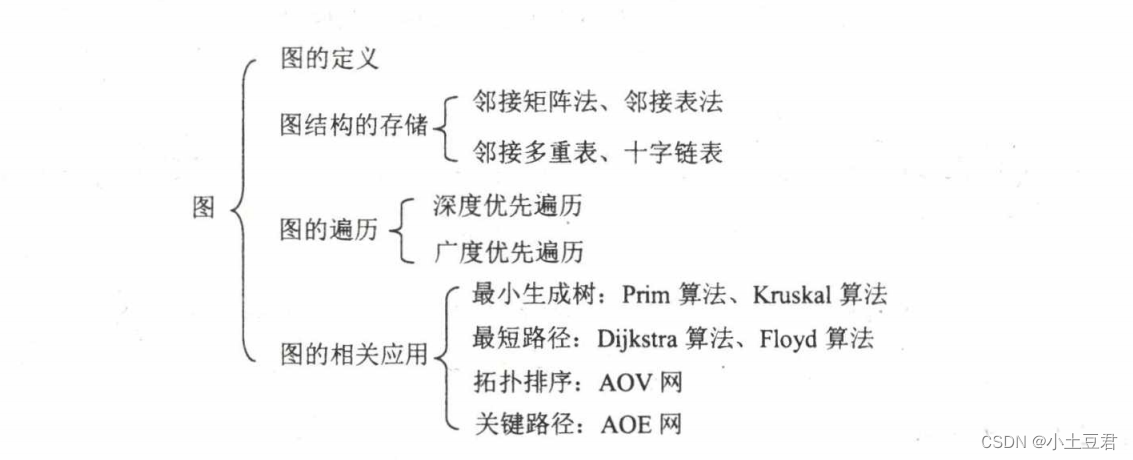
图的相关算法, 掌握其基本思想和实现步骤 , 而算法的具体实现不是重点 。
一、图的基本概念
1、定义
图G由顶点集V和边集E组成,记为G = (V,E)
①用|V|表示图 G 中顶点的个数, 用|E|表示图 G 中边的条数 。②图的顶点集|V| 一定非空
2、有向图
E是有向边(也称弧),则图G为有向图。弧是顶点的有序对,记为<v,w>,表示v指向w。
V称为弧尾,W称为弧头,<V, W>称为从V到W的弧,也称V邻接到W
3、无向图
若
E
是无向边(简称边)
,
则图
G
为无向图
。
边是顶点的无序对
,
记为
(v,
w) 或(w,v
)
W 和 V 互为邻接点 。 边 ( V, W ) 依附于 W 和 V, 或称边 ( V, W ) 和 V, W 相关联
4、完全图(也称简单完全图)
任意两个顶点之间都存在边就为完全图。
在有向完全图中任意两个顶点之间都存在方向相反的两条弧 。
5. 子图
图A所有的点和边都能在 图B的点集V和边集E中找到,则图A为图B的子集。
若图A含有图B所有的点,则A是B的
生成子图。
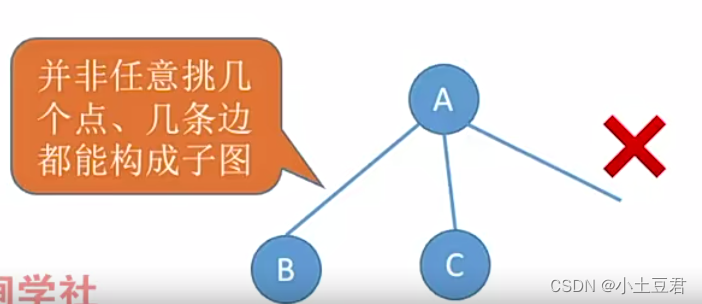
并非图A中V 和 E 的任何子集都能构成A 的子图 , 因为这样的子集可能不是图 , 即 E 的子集中的某些边关联的顶点可能不在这个V的子集中。下例中,后图形连图都不算,虽都是子集,但不是子图
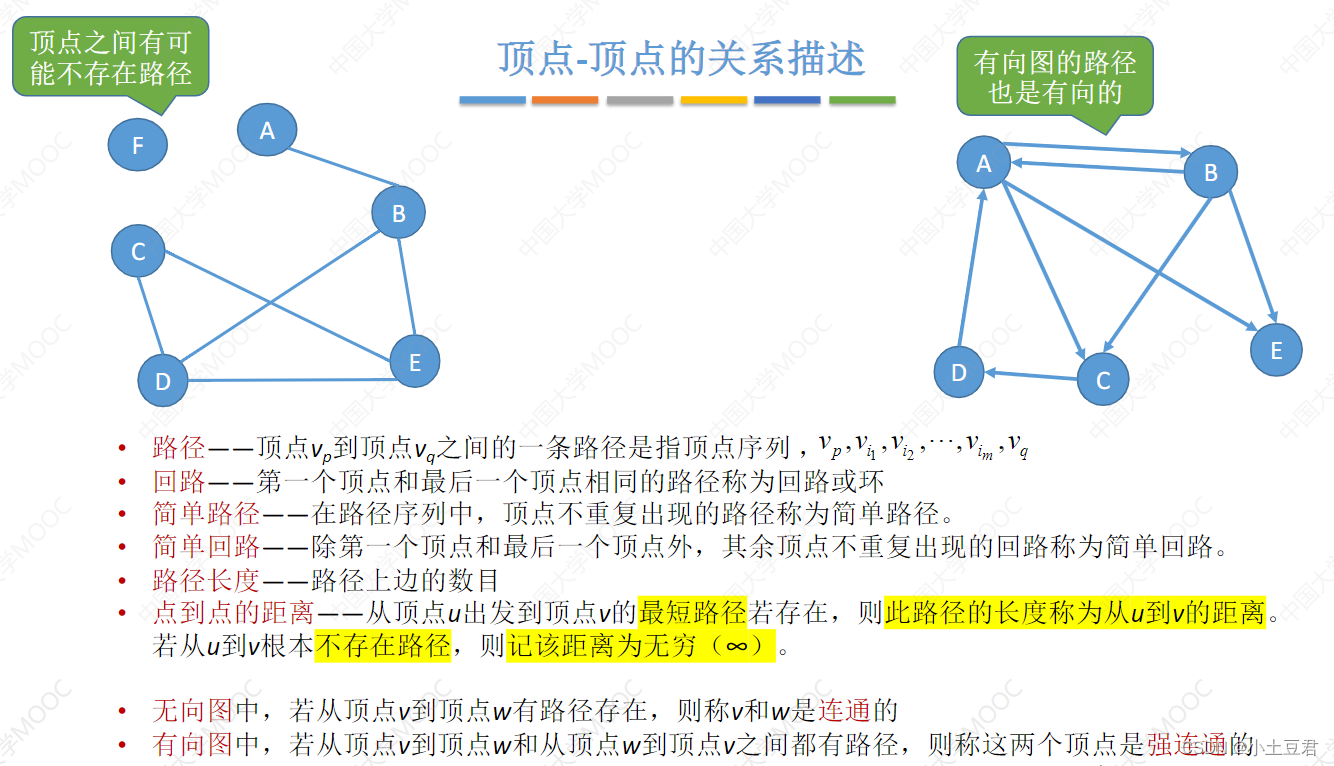
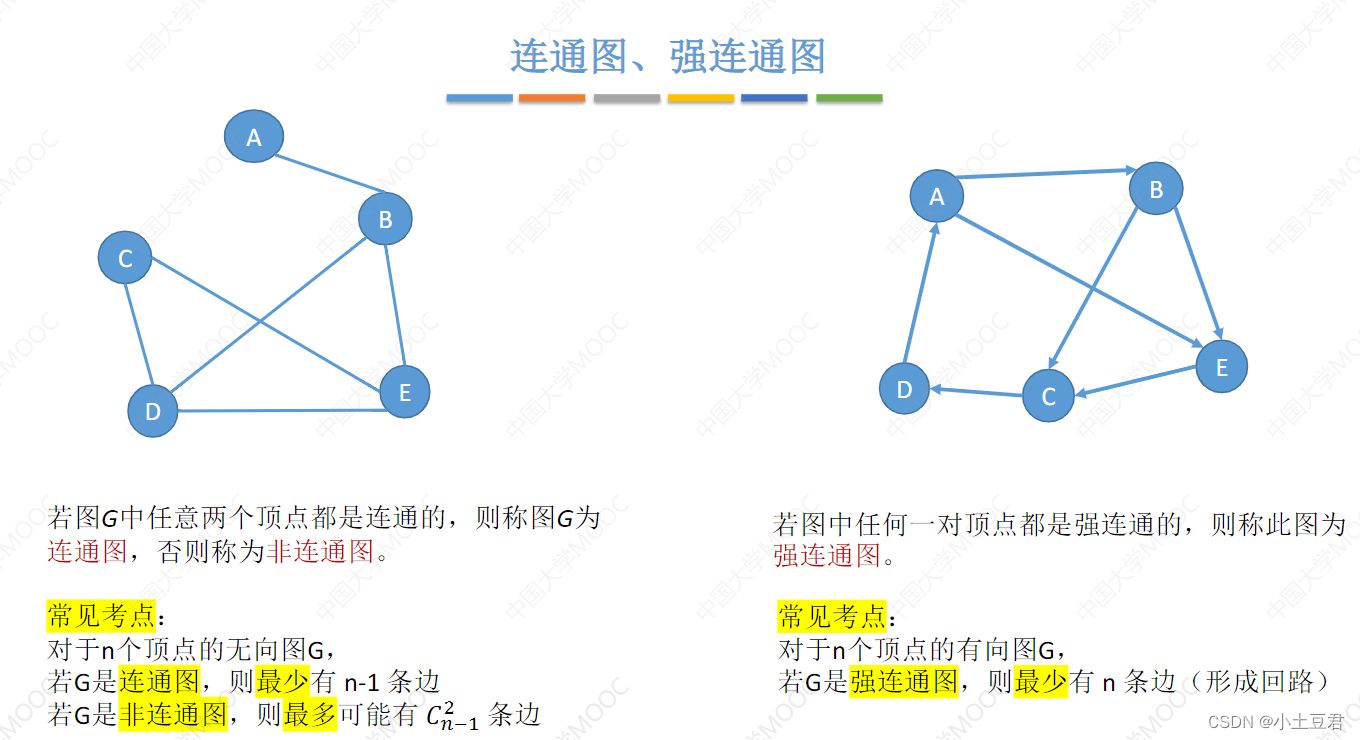
6、连通图、路径
连通:两个点有线连接起来,可能是一条线或者多条。
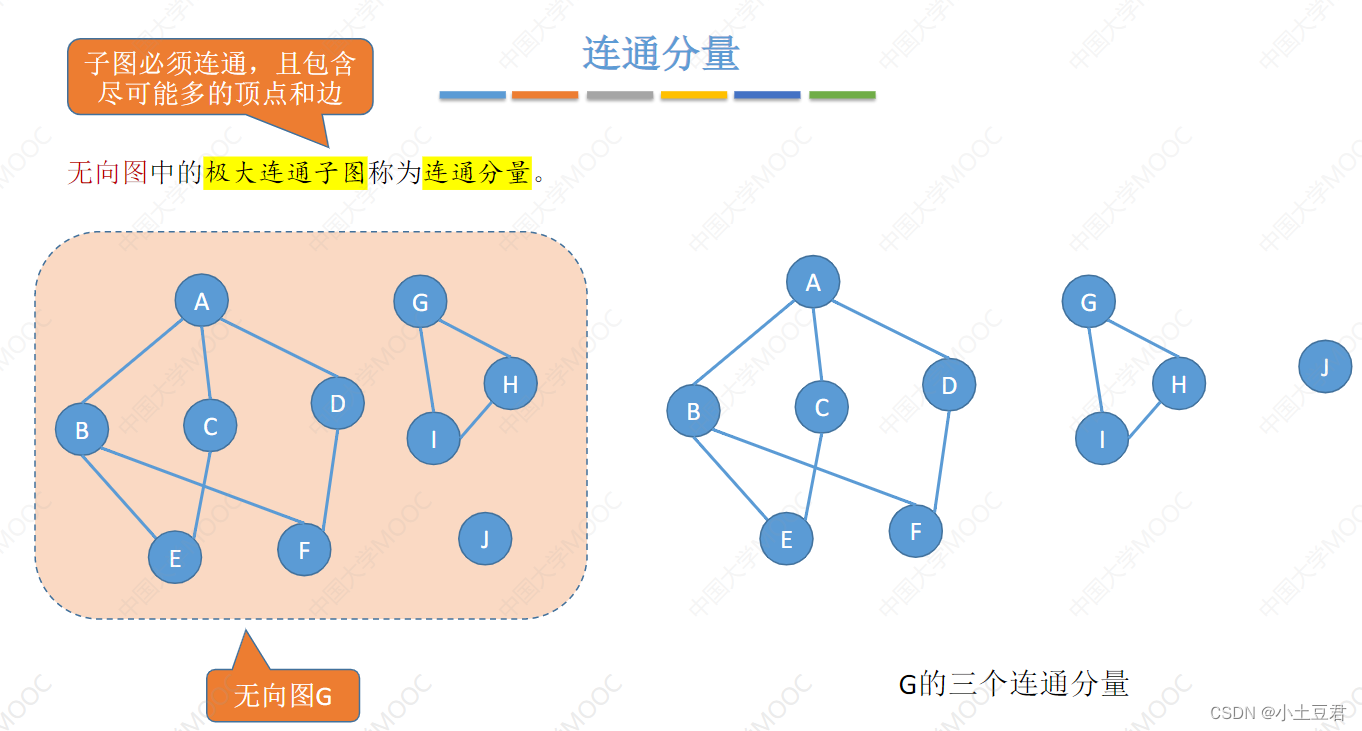
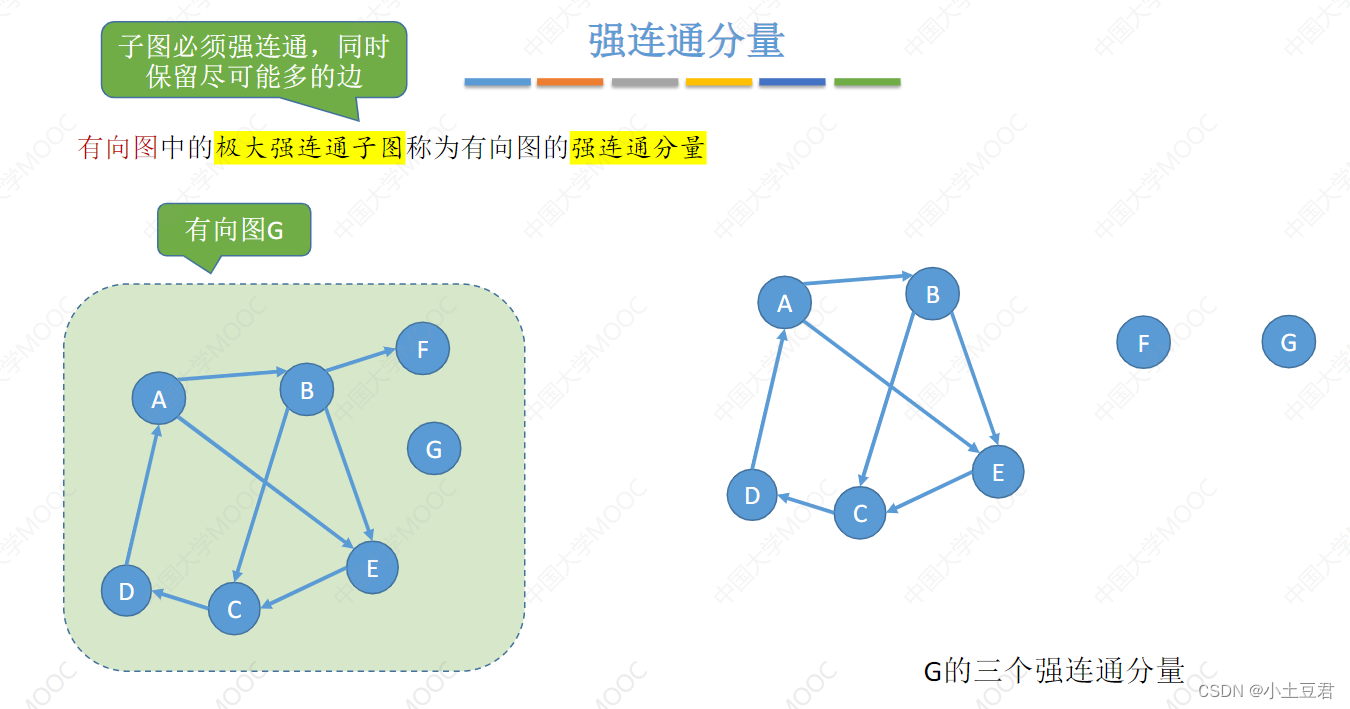
7、连通分量
能成原图中剥离出来的最大连通子图
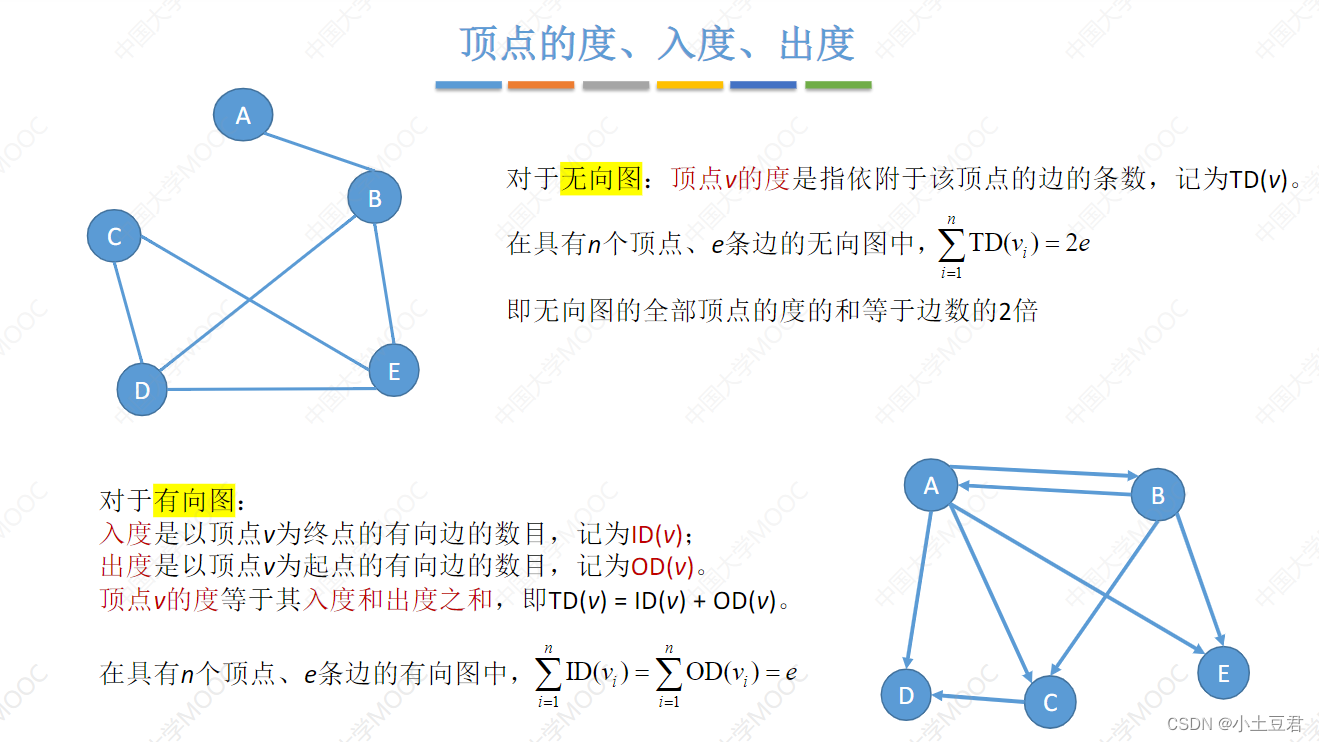
8、度
9、生成树

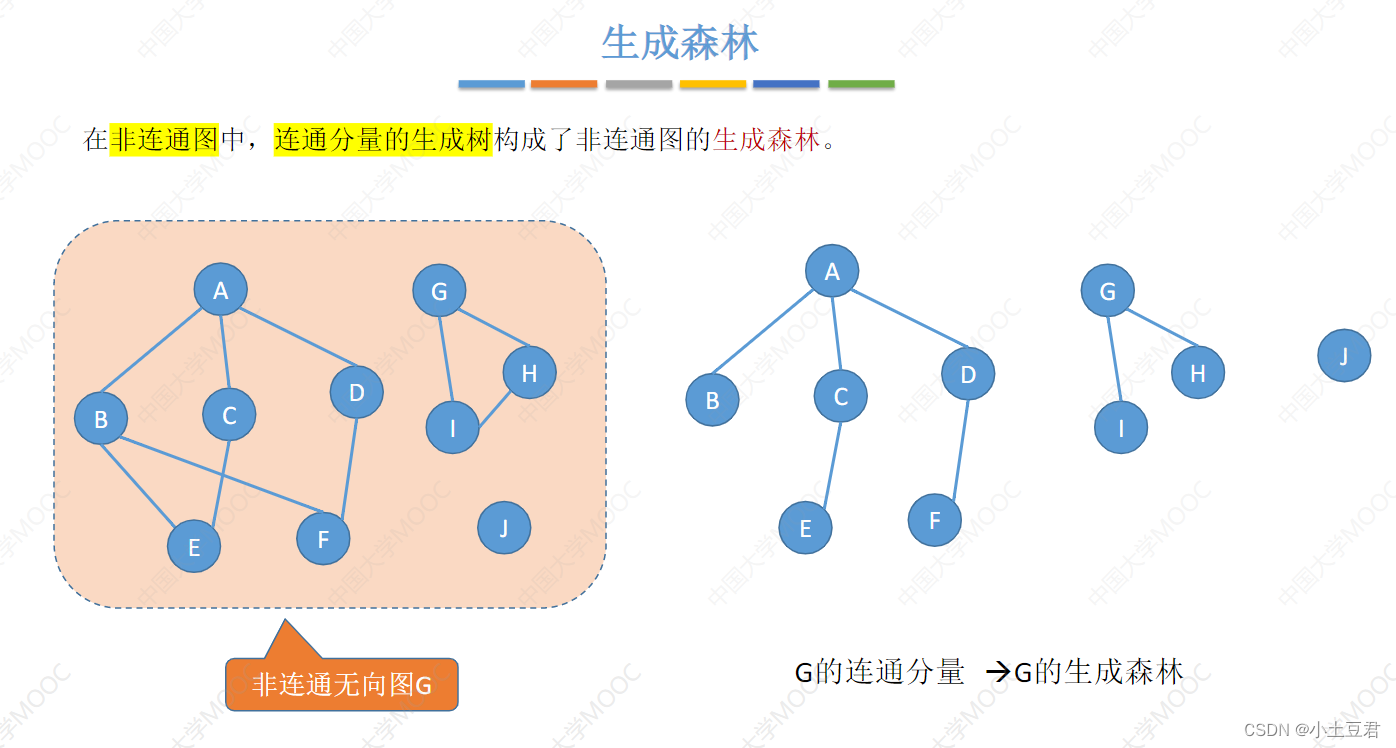
10、生成森林
生成森林 就是生成几个树,
11、 边的权和网
在一个图中
,
每条边都可以标上具有某种含义的数值
,
该数值称为该边的权值
。
这种边上带
有权值的图称为带权图
,
也称网
。
12、稠密图、稀疏图
边数很少的图称为稀疏图
,
反之称为稠密图
。
13、有向树
一个顶点的入度为
0
、
其余顶点的入度均为
1
的有向图
,
称为有向树
。
二、图结构的存储
1、邻接矩阵法
如下:图的结构都可由下图的矩阵表来表示,1代表两点之间有边,有向图中,1表示该行的点有指向该列的边

可以设置一个一维数组存储点集V,一个二位数组存上图的矩阵表,即存储边集,从而实现图的存储。代码如下:

①
无向图的邻接矩阵一定是一个对称矩阵(并且唯一)
。
因此
,
在实际存储邻接矩阵时只需
存储上(或下)三角矩阵的元素
。
②
对于无向图
,
邻接i
行
非零元素
的个数正好是顶点 i 的度
TD(v)
③
对于有向图,邻接矩阵的第i
行非零元素
个数正好是顶点i
的出度
OD(V); 第i列非零元素
个数正好是顶点i
的入度
ID(V)
④
用邻接矩阵存储图
,
很容易确定图中任意两个顶点之间是否有边相连
。
但是
,
要确定图
中有多少条边
,
则必须按行
、
按列对每个元素进行检测
,
所花费的时间代价很大
。
⑤
稠密图适合使用邻接矩阵的存储表示
。
2、邻接表法
当图为稀疏图时
,
使用邻接矩阵法显然要浪费大量的存储空间
,
而图的邻接表法结合了
顺序存储和链式存储方法
,
大大减少了这种不必要的浪费
。

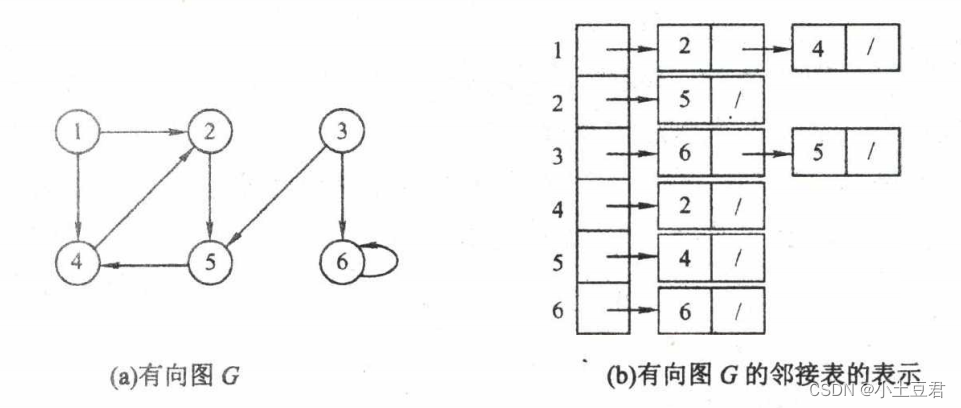
邻接表
,☞
对
每个顶点
,
建立一个单链表
,
单链表中的结点表示依附该顶点
的边
,
这个单链表就称为
边表
(对于有向图则称为出边表)。
边表的头指针和顶点的数据信息采用顺序存储(称为
顶点表
)。
所以在邻接表中存在两种结点:
顶点表结点和边表结点



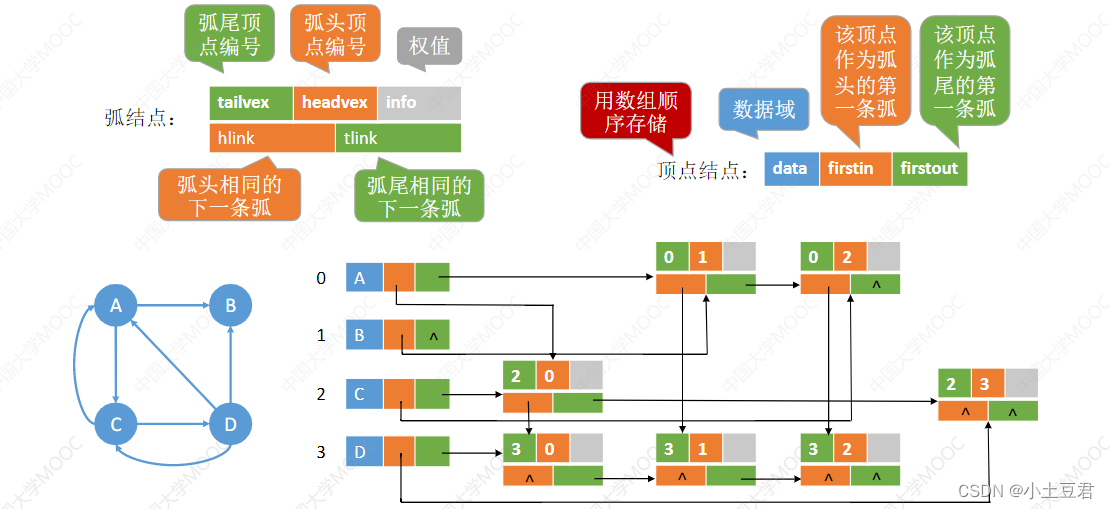
3、十字链表法
十字链表是有向图的一种链式存储结构
。
弧对应一个结点,
每个顶点对应一个结点
。
这些结点的结构如下图所示
。

弧结点中有
5
个域
:
tailvex
和
headvex
两个域分别指示弧尾和弧头这两个顶点的编号
;
hlink
域指向弧头相同的下一个弧结点
;
tlink
域指向弧尾相同的下一个弧结点
;
info
域存放该弧的相关信息。
这样
,
弧头相同的弧就在同一个链表上
,
弧尾相同的弧也在同一个链表上
。
顶点结点中有3
个域
:
data
域存放该顶点的数据信息
,
如顶点名称
;
firstin
域指向以该顶点为弧头的第一个弧结点;
firstout
域指向以该顶点为弧尾的第一个弧结点
。
注意
,
顶点结点之间是顺序存储的
4、邻接多重表
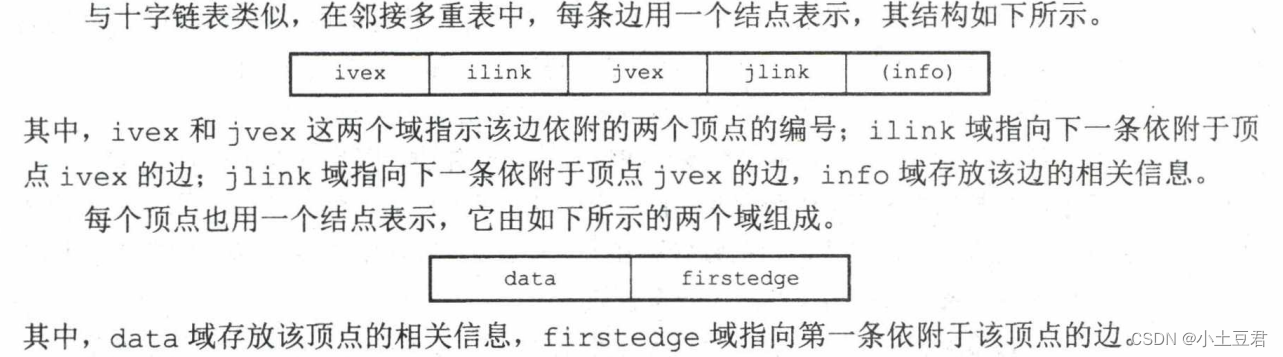
在邻接多重表中 , 所有依附于同一顶点的边串联在同一链表中 , 由于每条边依附于两个顶点,因此每个边结点同时链接在两个链表中 。对无向图而言 , 其邻接多重表和邻接表的差别仅在于 ,同一条边在邻接表中用两个结点表示, 而在邻接多重表中只有一个结点
5、基本操作

三、图的遍历
1、广度优先搜索
广度优先搜索思想:
首先访问起始顶点V,
接着由
V
出发
,
依次访问
V
的各个未访问过的邻接顶点然后依
次访问
wi,
的,
…
,
m
的所有未被访问过的邻接顶点
;
再从这些访问过的顶点出发
,
访问它们所有
未被访问过的邻接顶点
,
直至图中所有顶点都被访问过为止
。
若此时图中尚有顶点未被访问
,
则
另选图中一个未曾被访问的顶点作为始点
,
重复上述过程
,
直至图中所有顶点都被访问到为止
。
①它是一种 分层的查找过程 , 每向前走一步可能访问一批顶点,②不像深度优先搜索那样有往回退的情况 , 因此它是 非递归 的算法 。③为了实现逐层的访问, 算法必须借助一个辅助队列 , 以记忆正在访问的顶点的下一层顶点 。
伪代码:


第一大段代码的意义:能使其访问其他连通变量
BFS算法的性能分析
无论是邻接表还是邻接矩阵的存储方式,BFS算法都需要借助一个辅助队列Q, n个顶点均
需入队一次,在最坏的情况下,空间复杂度为O(|V|)。

BFS算法求解单源最短路径问题:


广度优先生成树
在广度遍历的过程中,我们可以得到一棵遍历树,称为广度优先生成树,同一个图的邻接矩阵存储表示是唯-的,故其广度优先生成树也是唯一的,但由于邻接表存储表示不唯一,故其广度优先生成树也是不唯一的。
2、深度优先搜索
深度优先搜索思想:
访问某一起始顶点
v ➡
访问与
v
邻接且未被访问的任意一个顶点w1 ➡
访问与w1邻接且未被访问的任意一个顶点的
…
…
重复上述过程
。
当不能再继续向下访问时,
依次退回到最近被访问的顶点
,
若它还有邻接顶点未被访问过
,
则从该点开始继续上述搜索过程,
直至图中所有顶点均被访问过为止
。
①图的邻接矩阵表示是唯一的,但对于邻接表来说,若边的输入次序不同,生成的邻接
表也不同 。②DFS 算法是一个递归算法 , 需要借助一个递归工作栈
DFS代码

DFS性能
DFS
算法是一个递归算法
,
需要借助一个递归工作栈
,
故其空间复杂度为O(|v|)
。
遍

深度优先的生成树和生成森林
与广度优先搜索一样
,
深度优先搜索也会产生一棵深度优先生成树
。当然
,
这是有条件的
,
即对连通图调用
DFS
才能产生深度优先生成树
,
否则产生的将是深度优先生成森林。

图的遍历与图的连通性

四、图的应用
1、最小生成树
在一个带权连通无向图G 权值之和最小的那棵生成树,就是最小生成树
首先了解什么是生成树?
生成树包含图的所有顶点 , 并且只含尽可能少的边 。对于生成树来说 , 若砍去它的一条边, 则会使生成树变成非连通图 ; 若给它增加一条边 , 则会形成图中的一条回路 。
性质
①最小生成树不是唯一的
G中的各边权值互不相等时,G的最小生成树是唯一的;
若无向连通图
G
的边数比顶点数少1,
即
G
本身是一棵树时
,
则
G
的最小生成树就是它本身
。
②
最小生成树的边的权值之和总是唯一的
③
最小生成树的边数为顶点数减
1
。
Prim (普里姆)算法
在图中任取一顶点 加入空树T, 之后选择与已取 顶点集合 距离最近的顶点 , 并将该顶点和相应的边加入T, 每次操作后T 中的顶点数和边数都增 1 。 以此类推 , 直至图中所有的顶点都并入T, 得到的 T 就是最小生成树 。
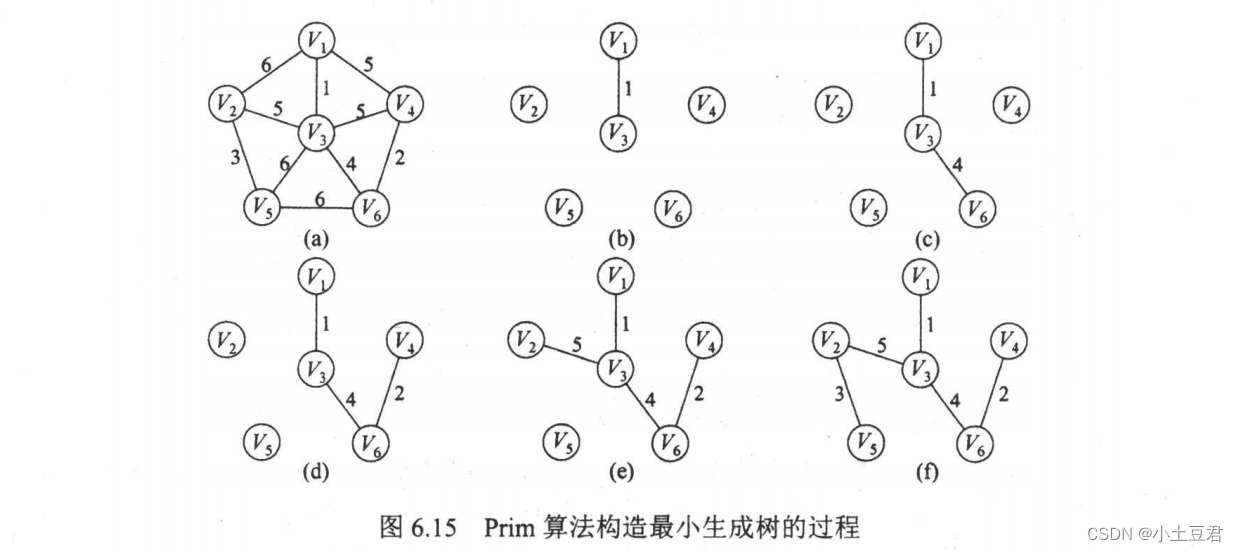

Kruskal (克鲁斯卡尔)算法
初始时为只有
n
个顶点而无边的非连通图
,
然后
不断选取当前未被选取过且权值最小的边,
直至
T
中所有顶点都在一 个连通分量上。


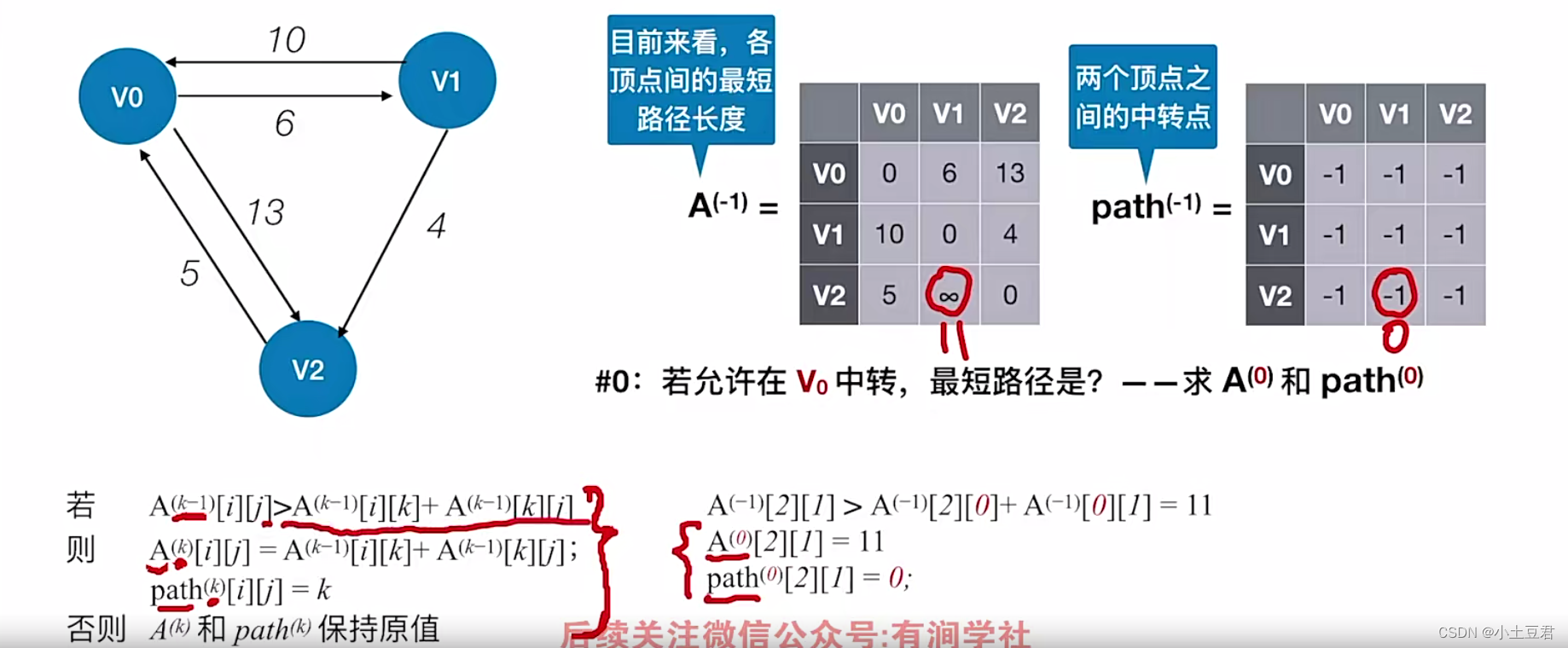
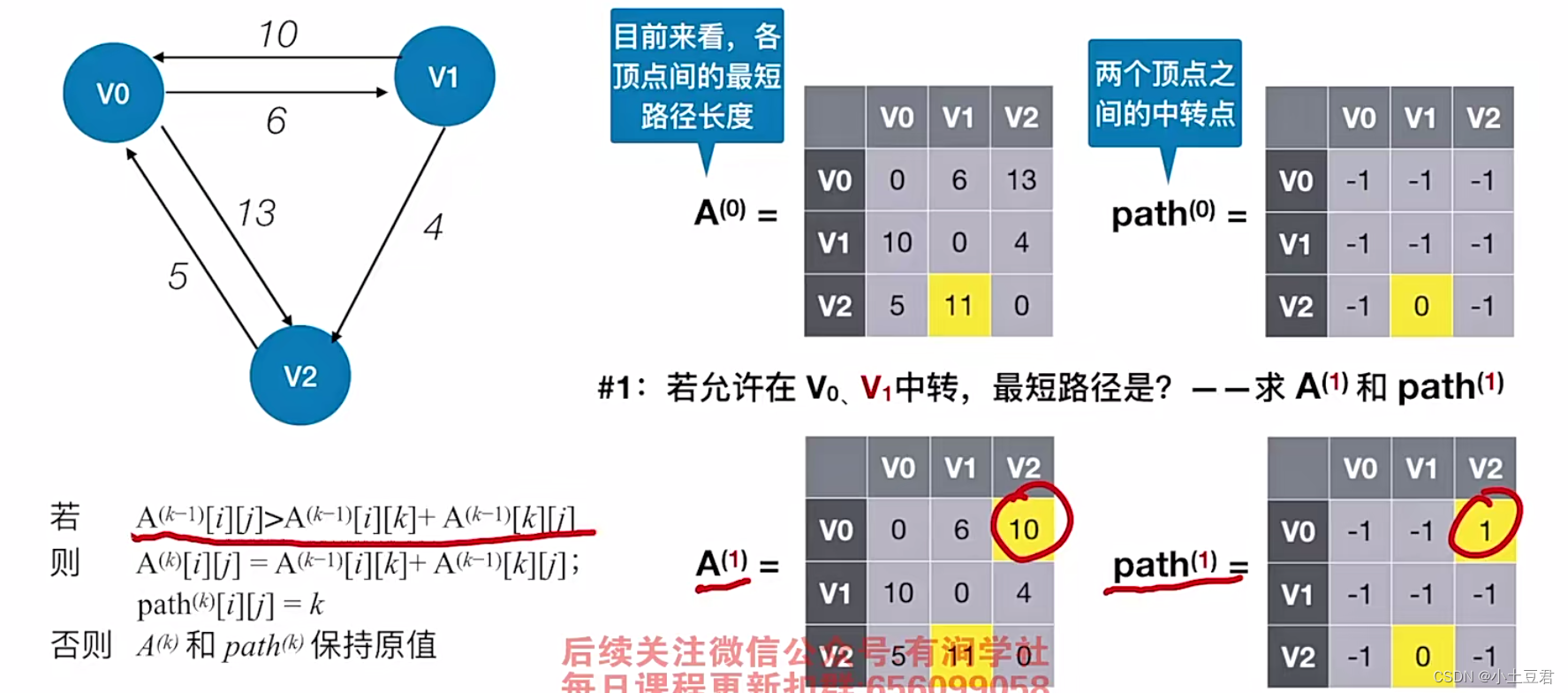
2、最短路径

最短路径
两点的路径中
所经过边上的权值之和最小的路径 为 最短路径。
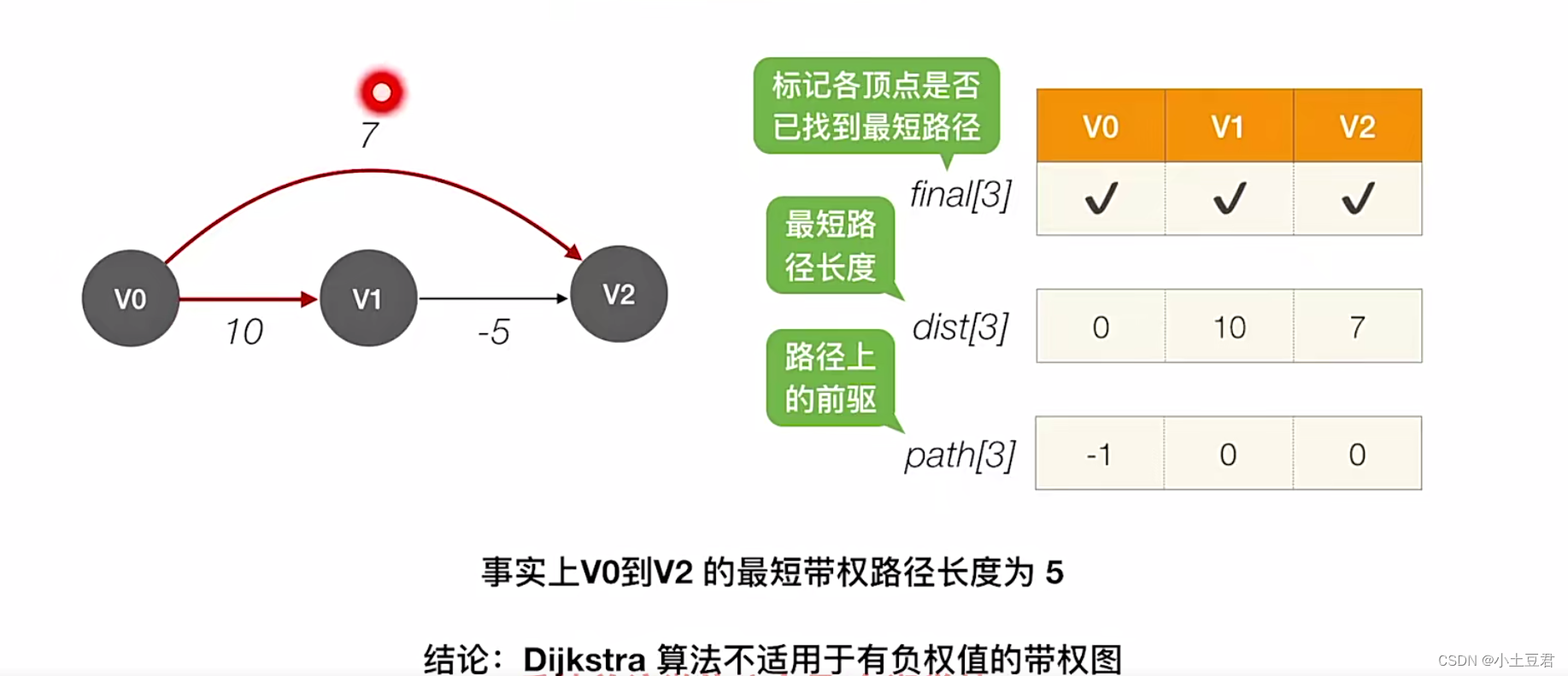
单源最短路径
即求图中某一顶点到其他各顶点的最短路径,
可通过经典的
Dijkstra
(
迪杰斯特拉
)
算法求解
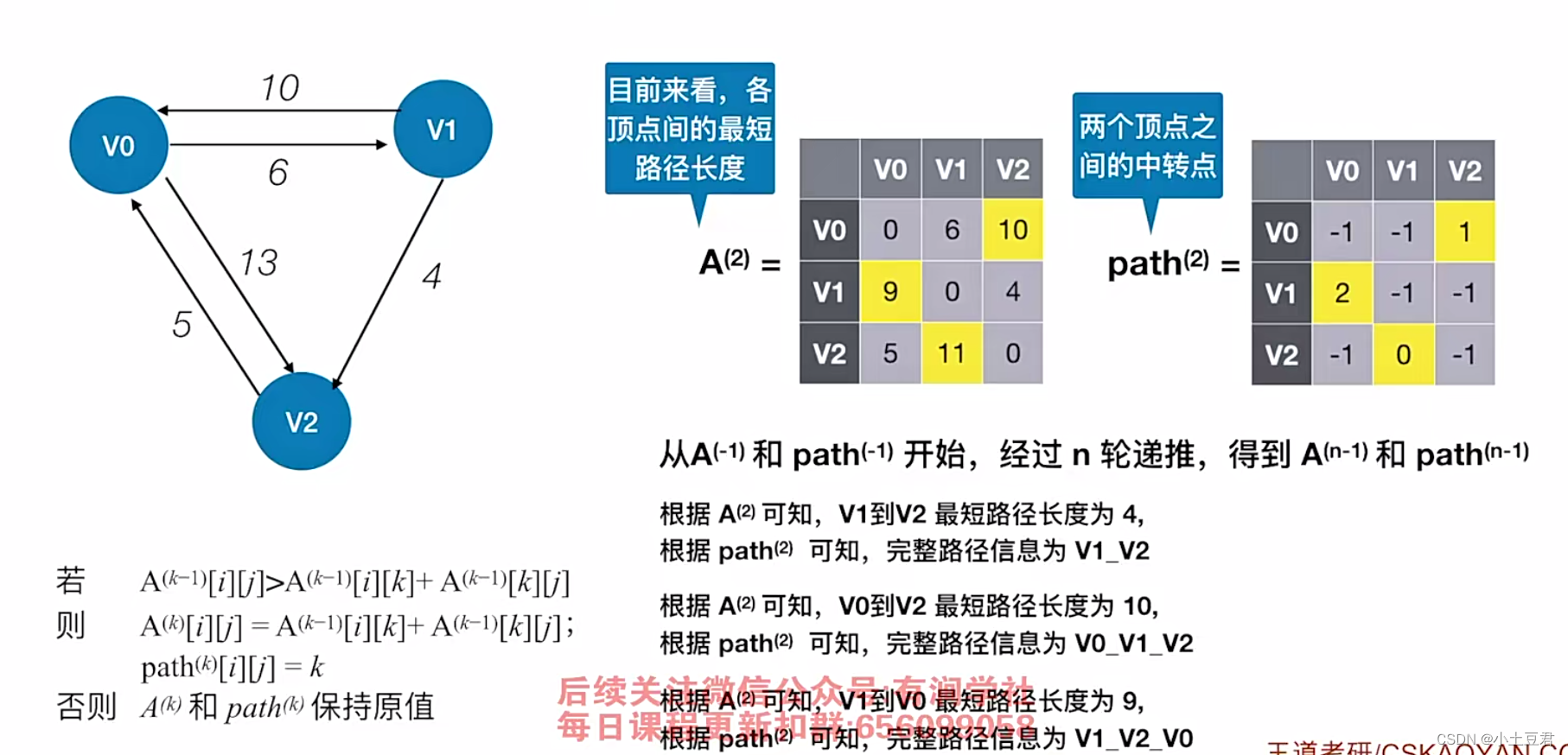
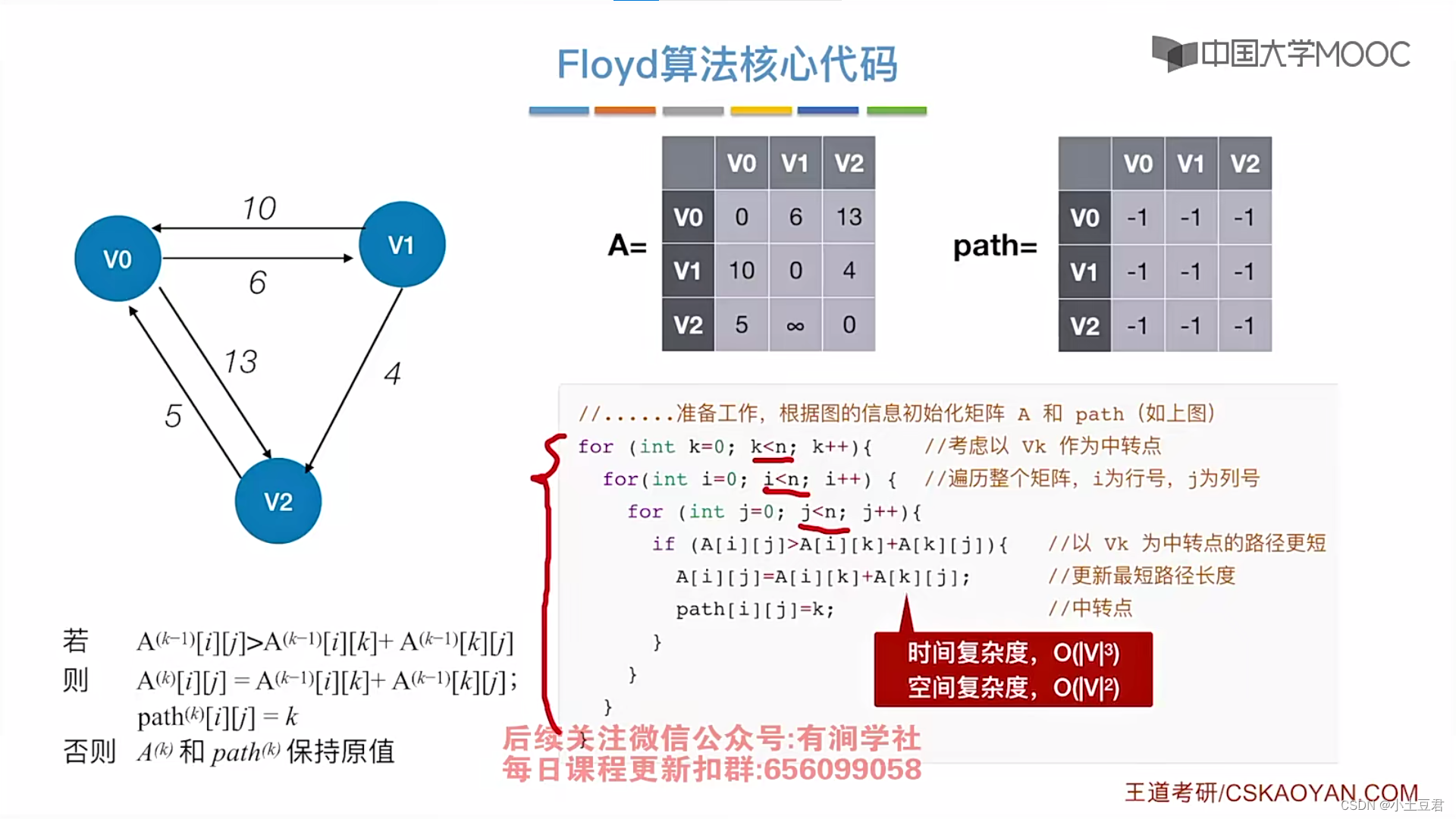
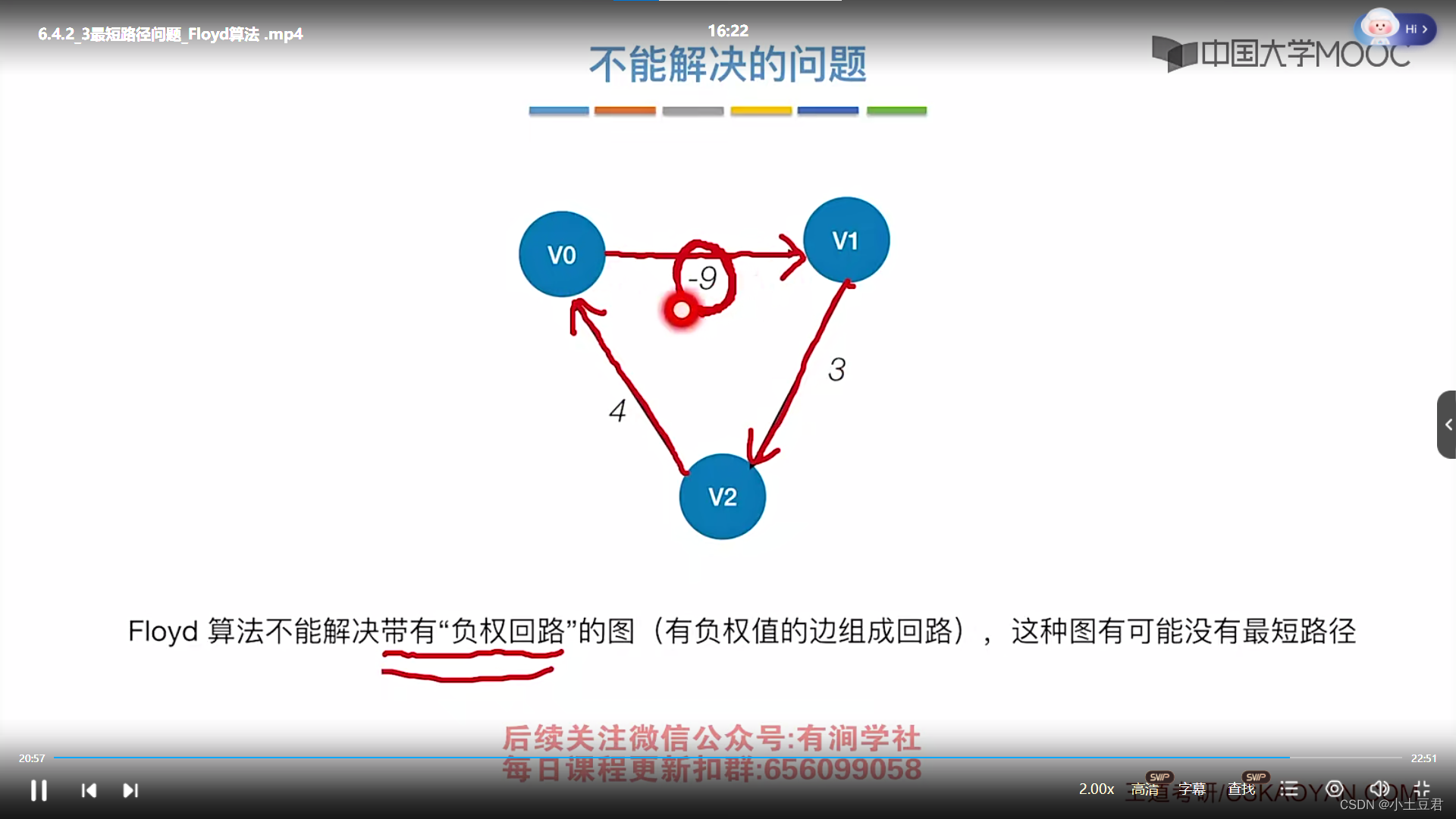
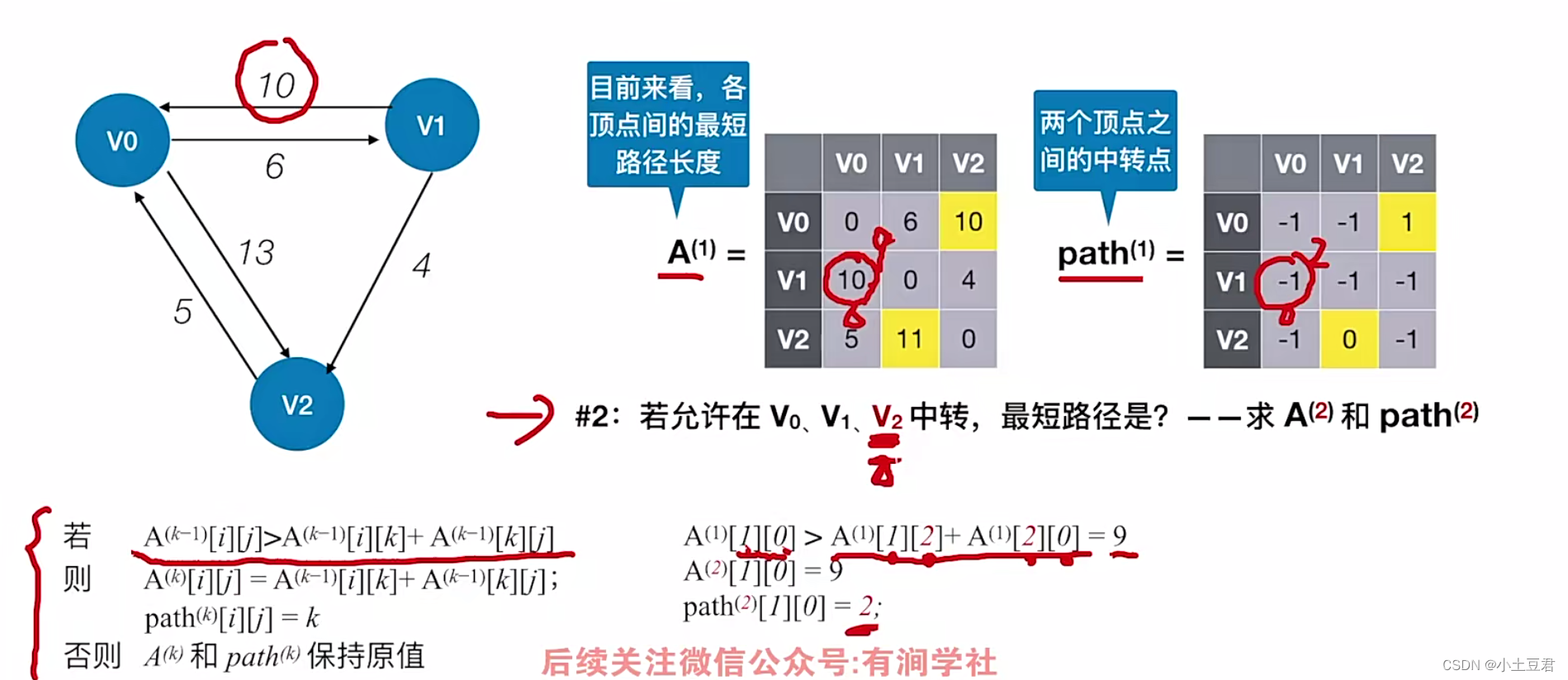
每对顶点间的最短路径, 可通过 Floyd ( 弗洛伊德 ) 算法来求解 。
BFS算法

Dijkstra (迪杰斯特拉)算法



Floyd (弗洛伊德)算法

有向无环图
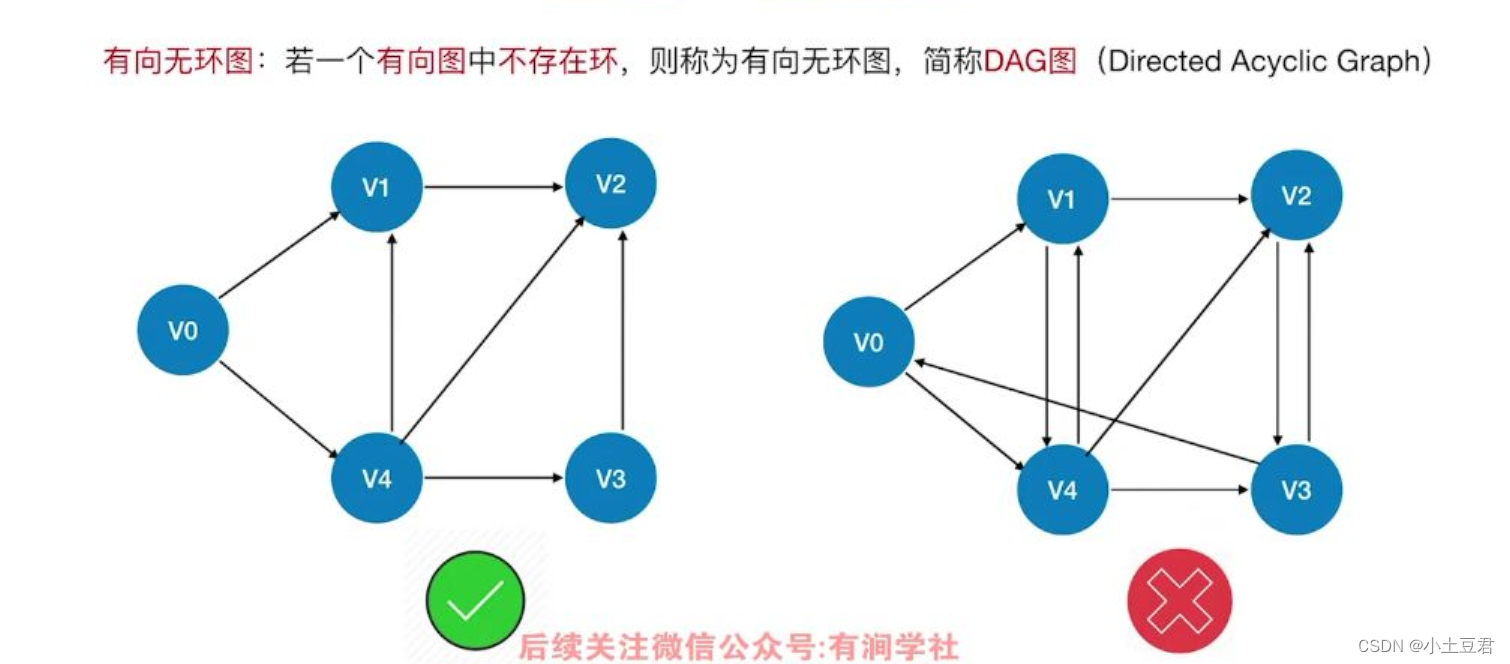

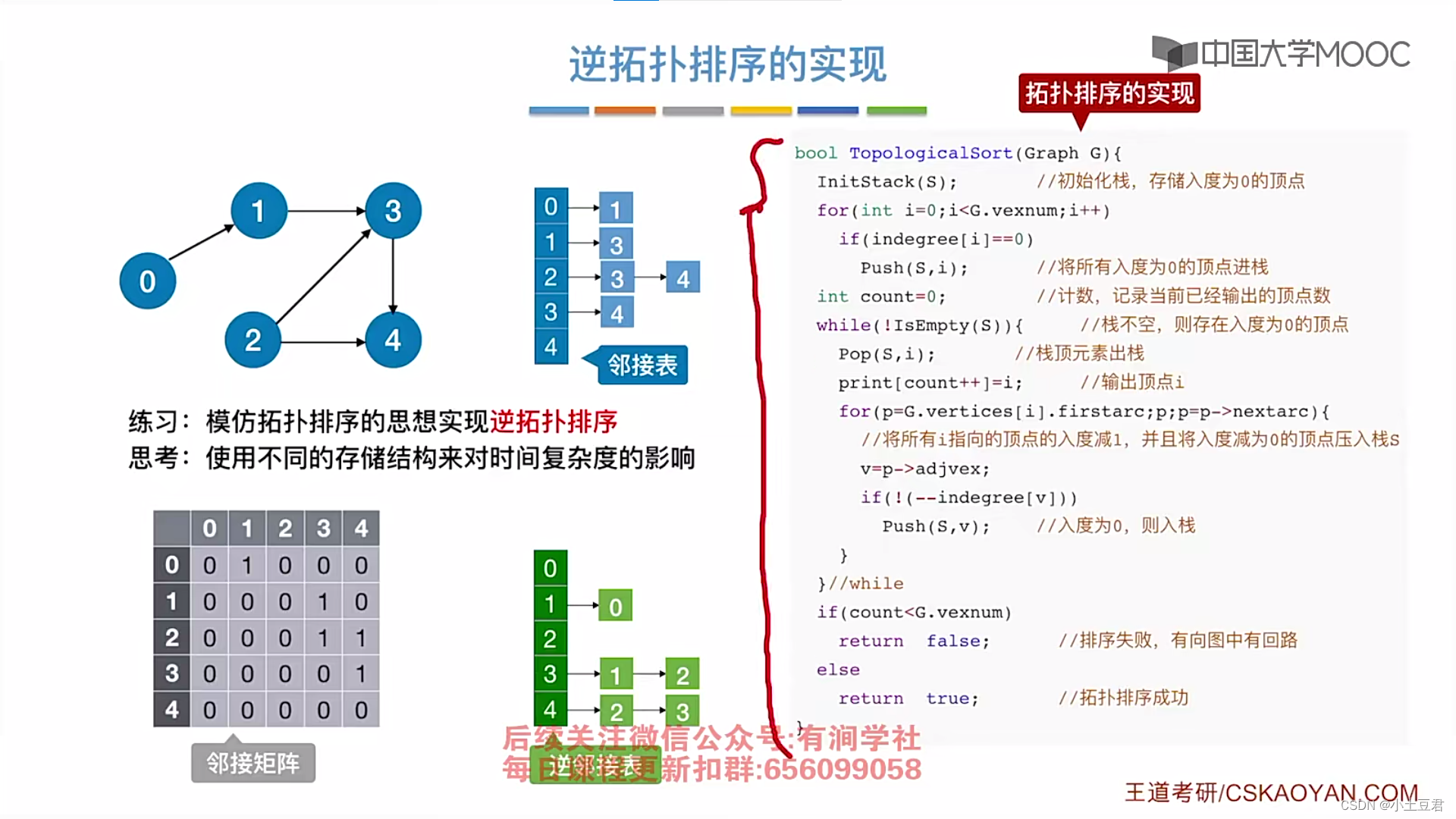
3、拓扑排序



逆拓扑排序

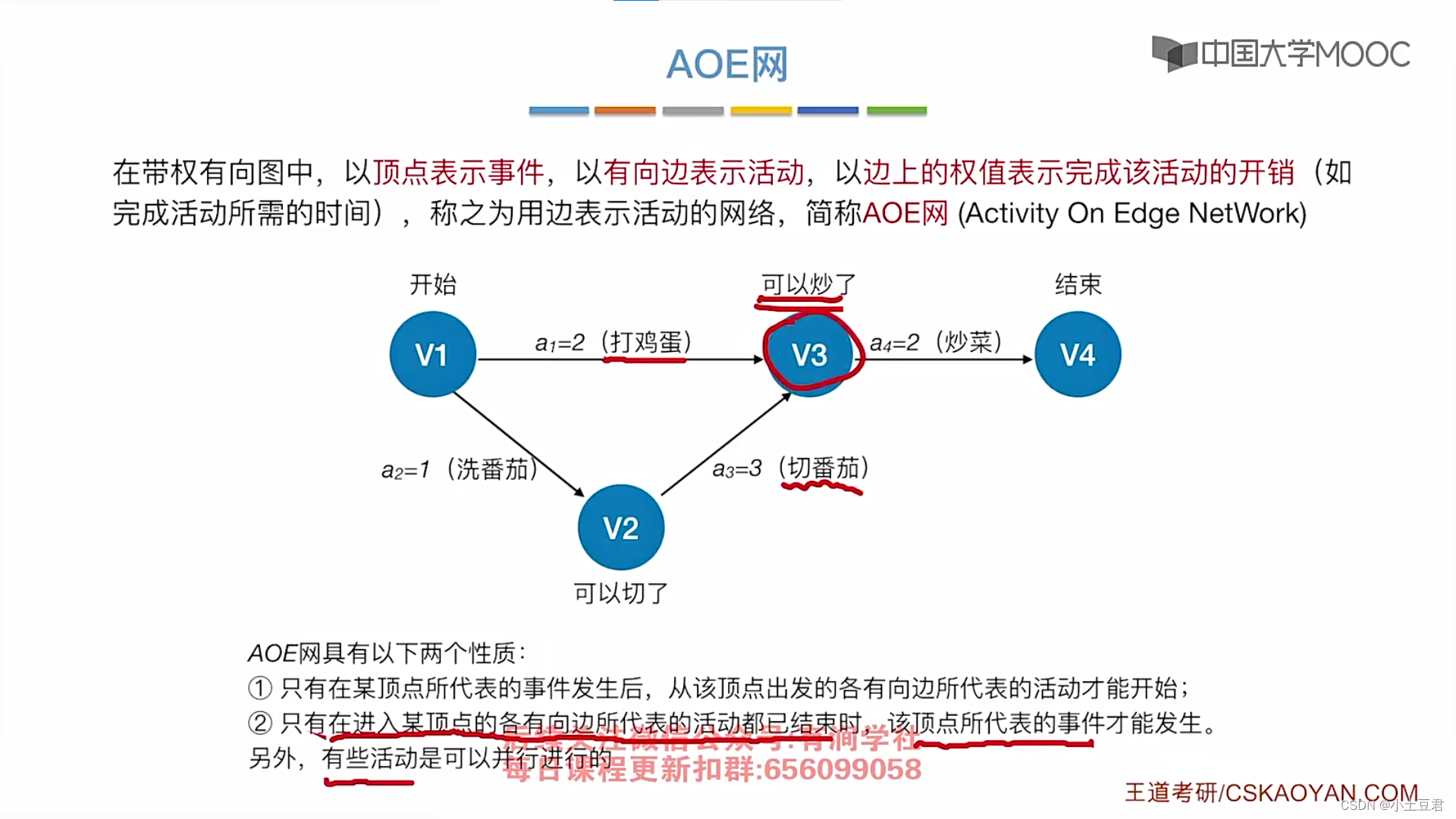
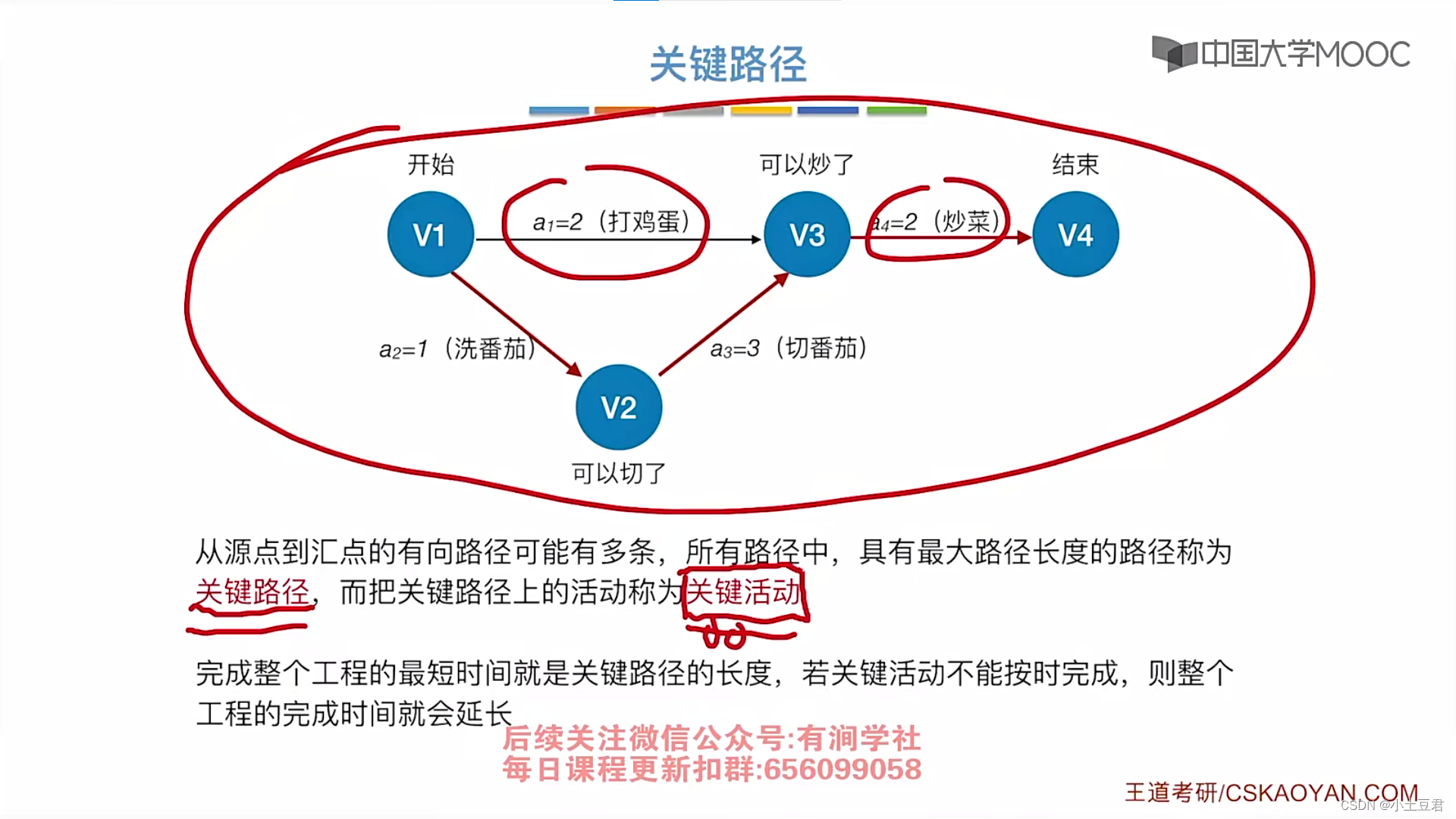
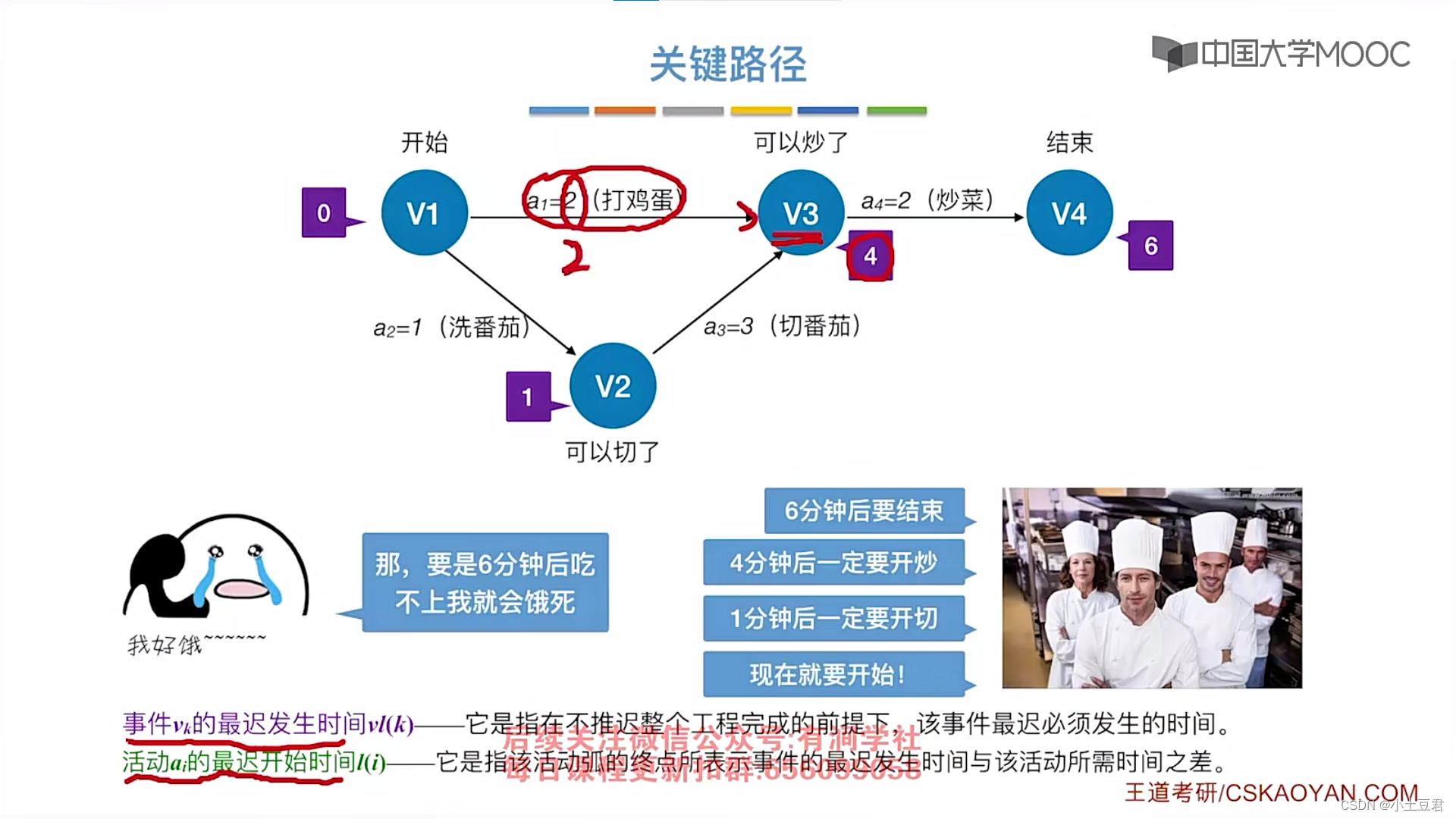
4、关键路径



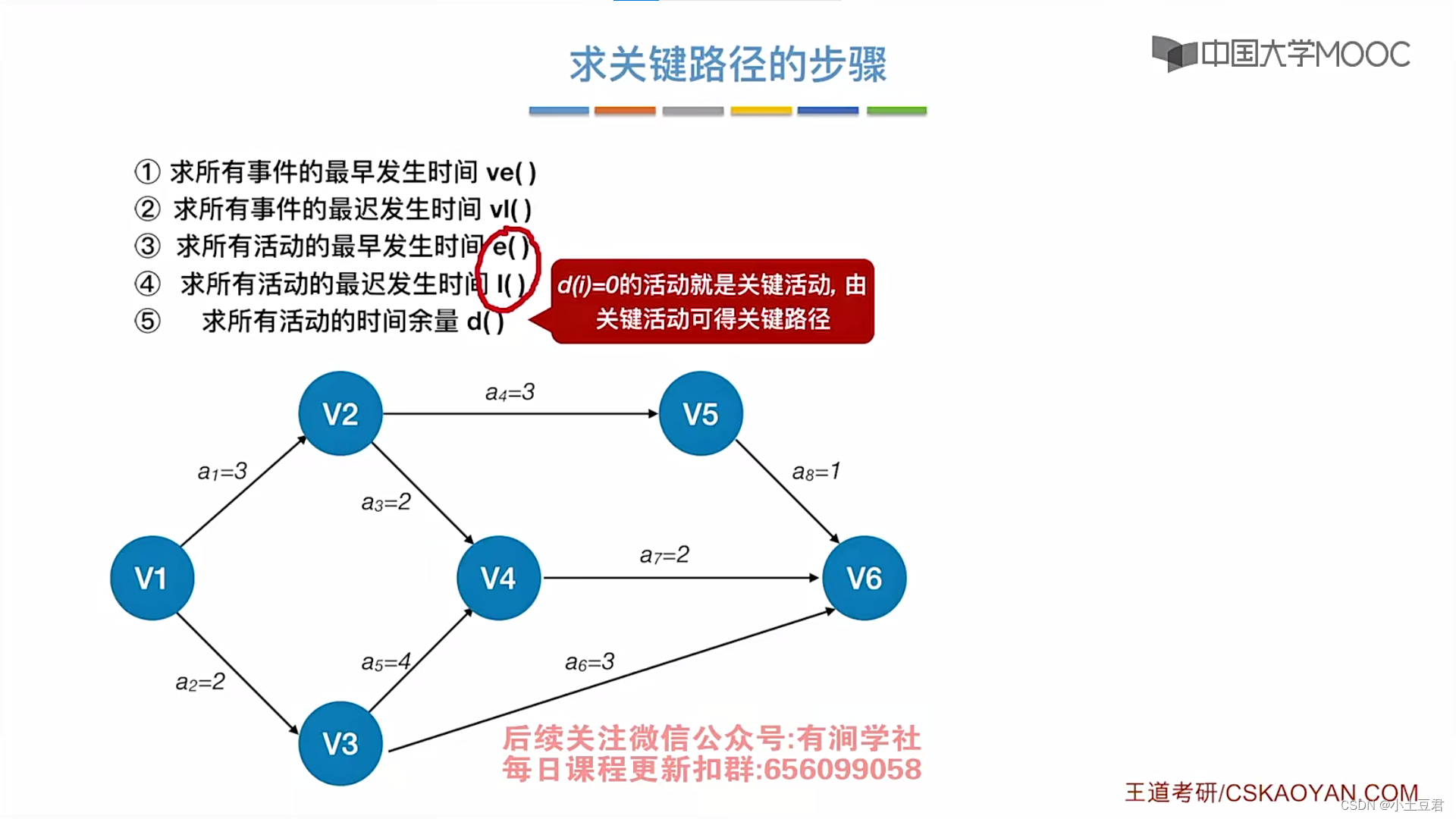

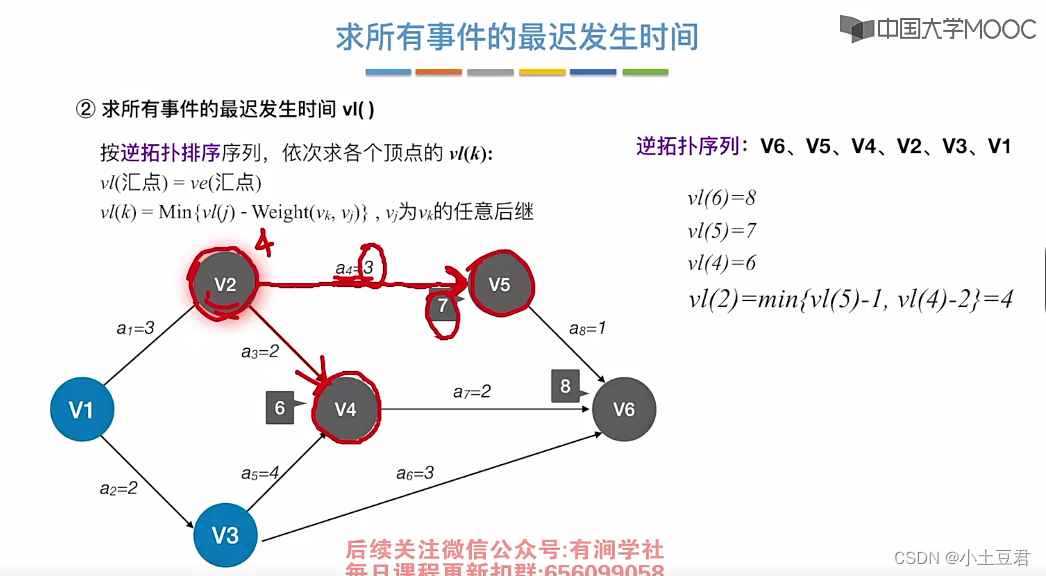
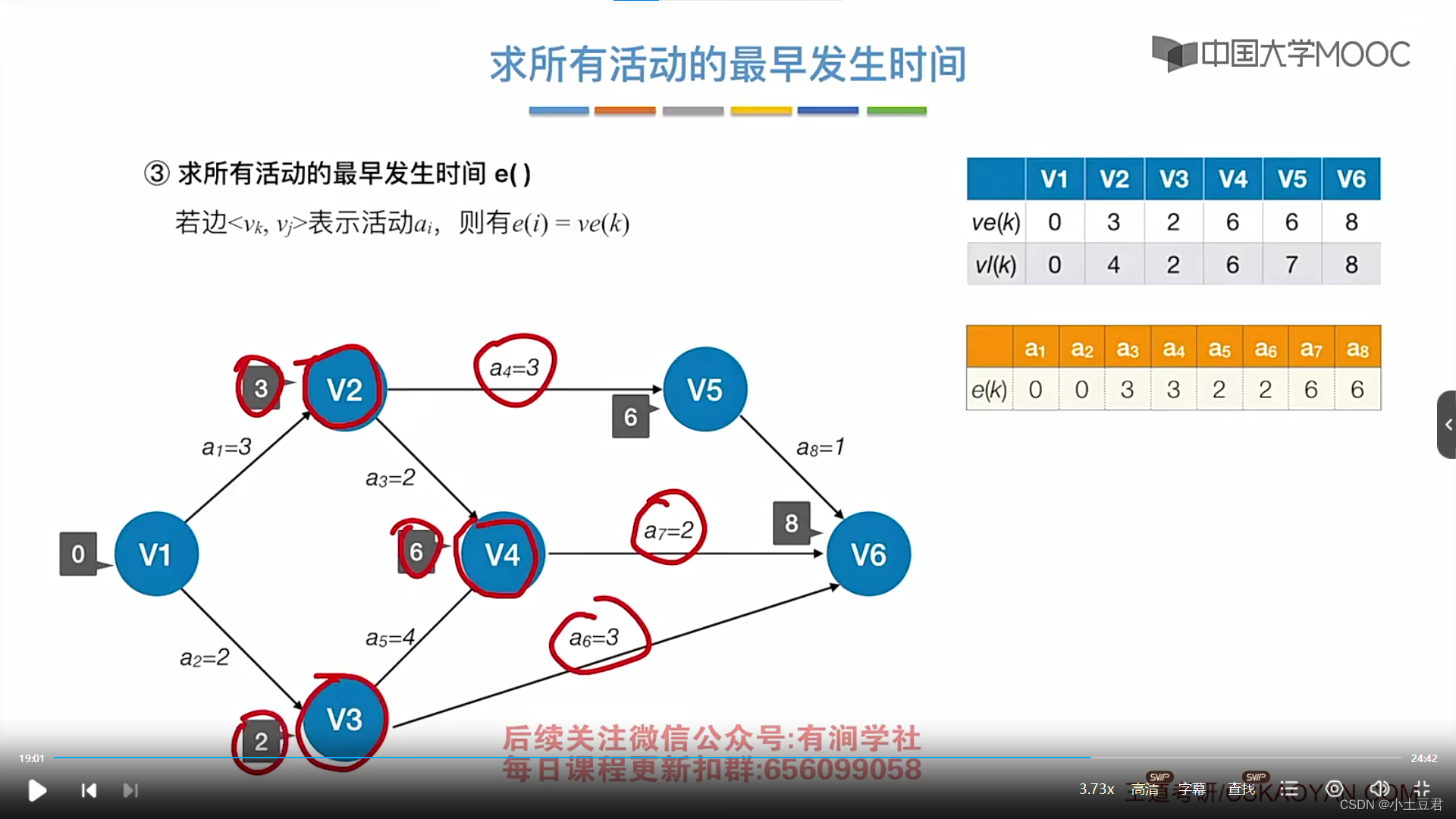

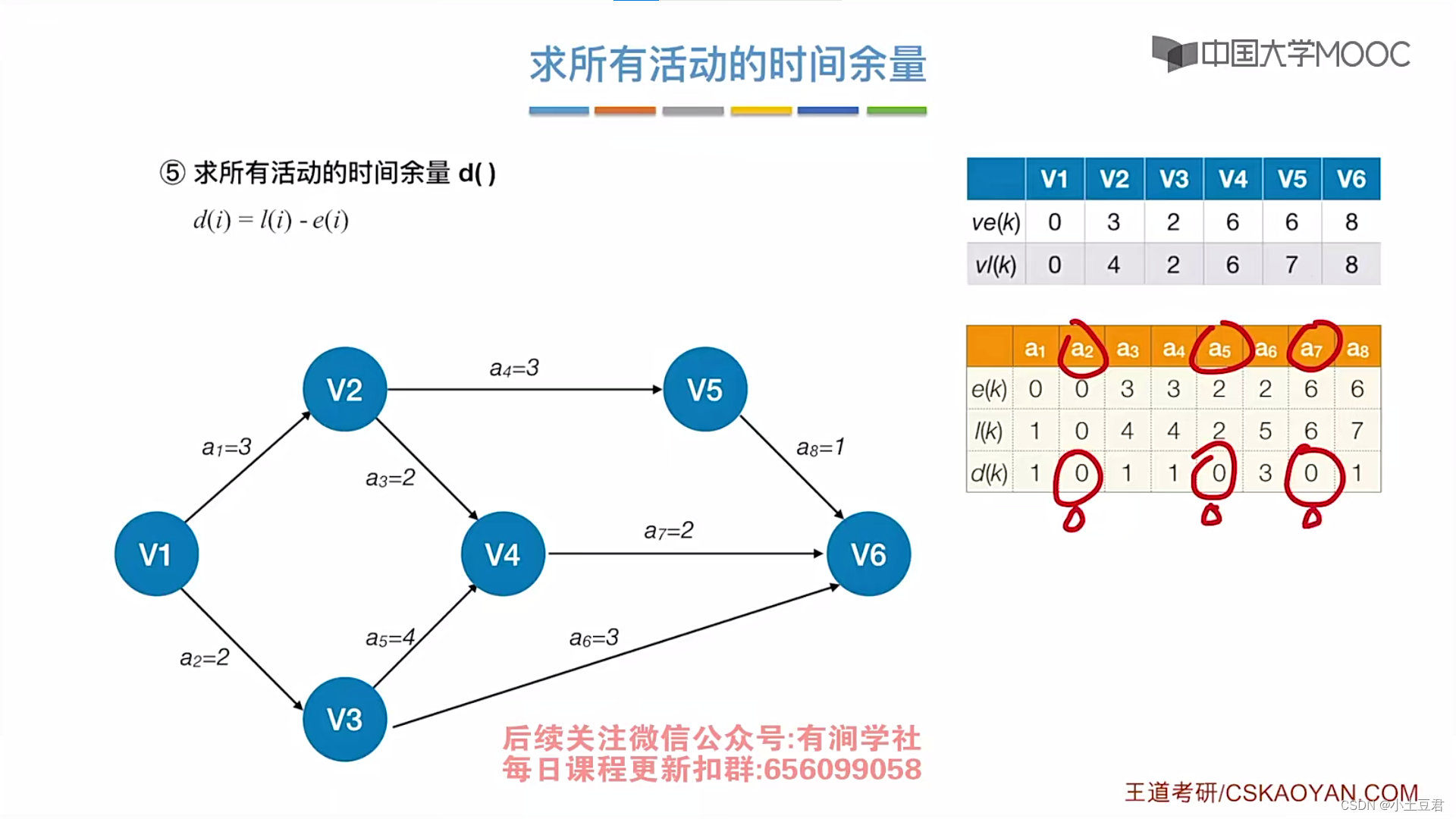
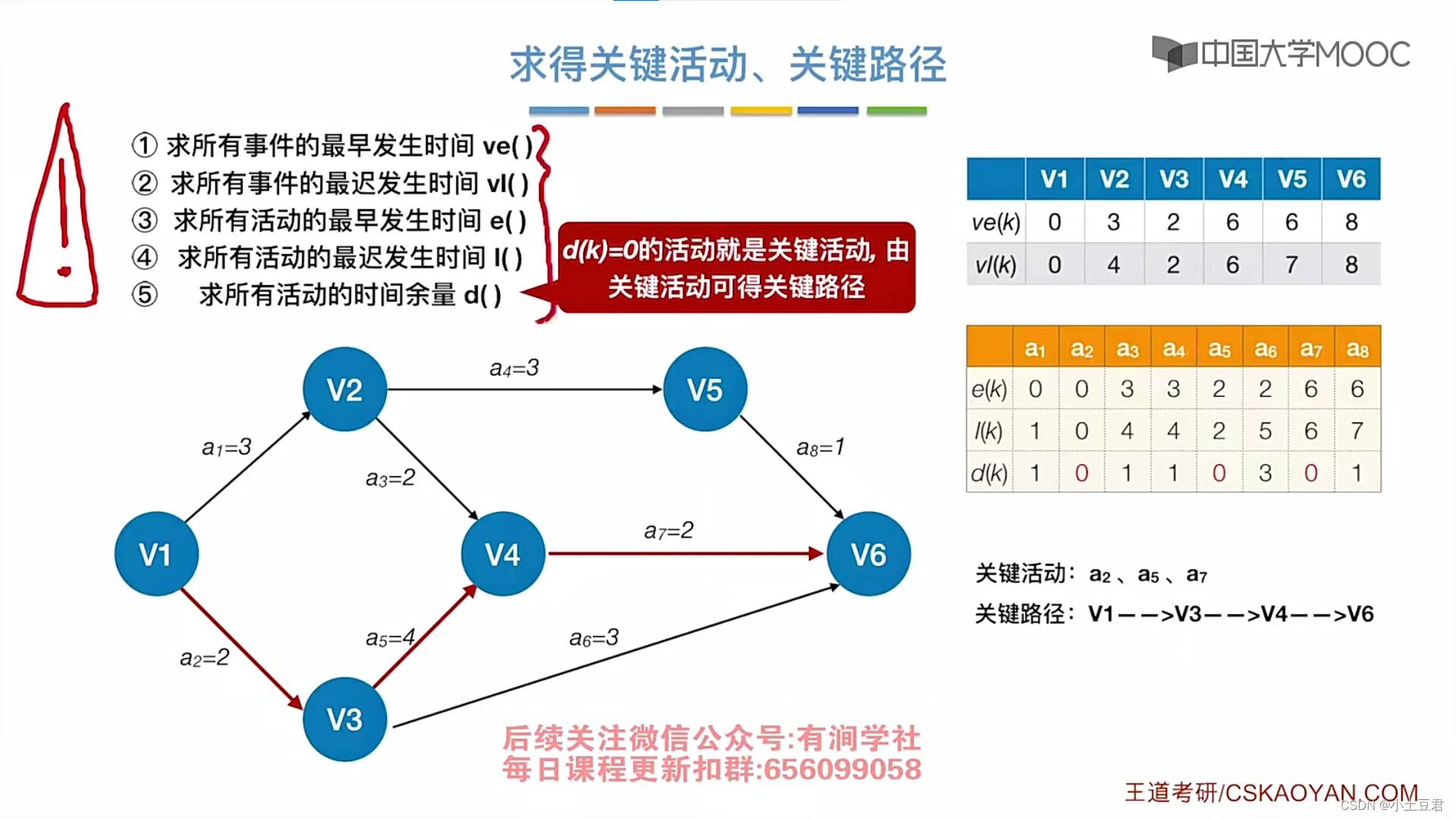









 本文介绍了图的基本概念,包括有向图、无向图、连通性和子图等,并详细讨论了图的存储结构(邻接矩阵和邻接表),以及广度优先搜索(BFS)和深度优先搜索(DFS)等图遍历算法。此外,还涉及了最小生成树、最短路径算法(如Dijkstra和Floyd)以及拓扑排序等内容。
本文介绍了图的基本概念,包括有向图、无向图、连通性和子图等,并详细讨论了图的存储结构(邻接矩阵和邻接表),以及广度优先搜索(BFS)和深度优先搜索(DFS)等图遍历算法。此外,还涉及了最小生成树、最短路径算法(如Dijkstra和Floyd)以及拓扑排序等内容。





























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








