数字游戏（解题过程记录）

提示：非最优解

---

题目

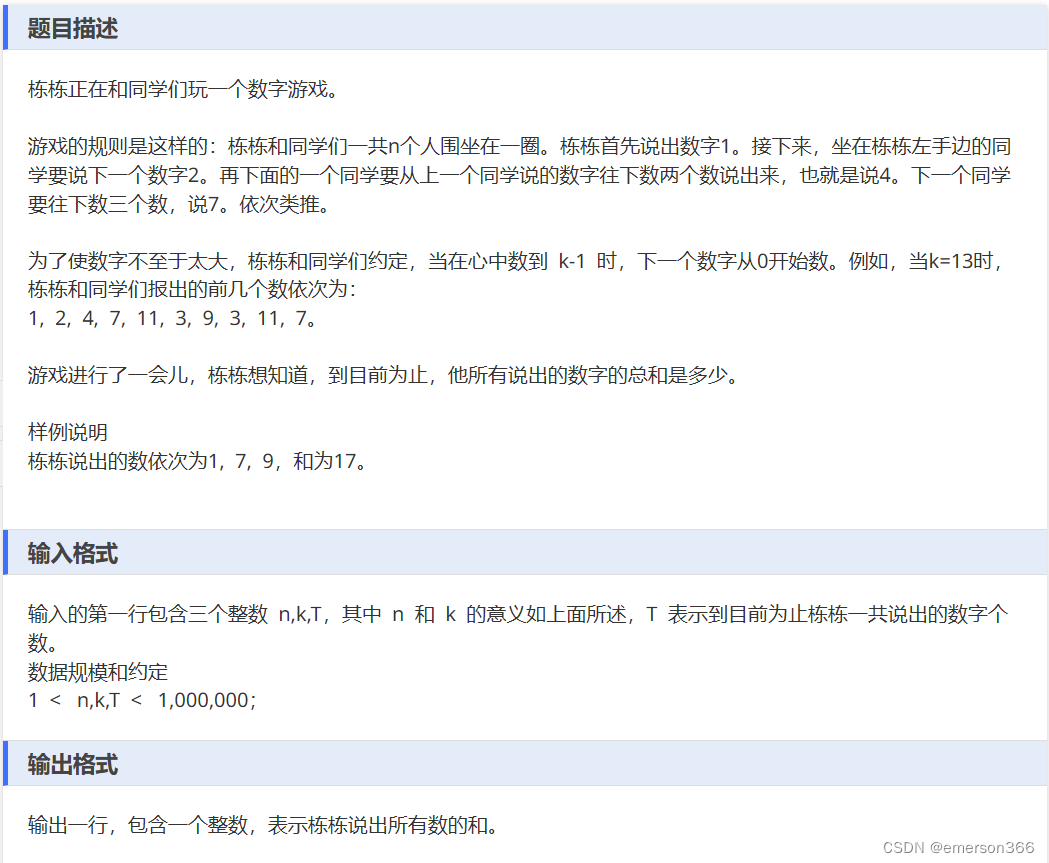
试错过程

• 思路1（失败）：循环相加，和%k即得结果，取第（n+1）的倍数个数相加，输出结果。
  • 结果：输出结果正确，但时间复杂度极高，导致测试超时。
• 思路2:等差数列求和，1+2+3+4+5+…+n与（n+1）+（n+2）+…+(n+n)之间差了n*n，只需要循环加n *n并%k,并对结果求和，循环t次，也可以得到结果
  • 结果：结果正确，数字太大数据溢出。
• 优化思路2：将(1+2+3+4+5+…+n)%k设为a，n*n设为b，只需要循环t次a=a+b,再用（x+a）对k取余即可得到结果
  • 注意点：n*n数据过大，用BigInteger来实现大数乘法

n=scan.nextInt();
String str=Integer.toString(n);
BigInteger temp=new BigInteger(str);
BigInteger res=temp.pow(2);//temp.multiply(temp)也可实现乘法
long b=res.longValue()%k;

循环累加法（思路2的代码实现）

import java.math.BigInteger;
import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int n,k,t;
        long sum=1;
        long a=0,b,x=1;
        n=scan.nextInt();//人数
        k=scan.nextInt();//上限
        t=scan.nextInt();//循环次数
        
        for(int i=1;i<=n;i++){
            a=a+i;
        }
        a=a%k;//得到初始部分的余数
        
        String str=Integer.toString(n);
        BigInteger temp=new BigInteger(str);
        BigInteger res=temp.pow(2);//第二轮每个数比第一轮每个数都大n，且有n个数
        b=res.longValue()%k;//得到累加部分的余数
        
        for(int i=1;i<t;i++){
            x=(x+a)%k;
            a=a+b;
            sum=sum+x;
        }
        System.out.println(sum);
    }
}

• 如果不用大数乘法可以用取模运算的分配率：(a* b)%p=(a%p*b%p)%p；