自适应滤波器可以用lms算法来实现,使得输出均方误差最小,即d(n)和y(n)最相似,则可以得到未知系统的幅频响应。
%Example 2.3.2:system identification
a=[1 -1.6 1.75 -1.43 0.6814 -0.1134 -0.0648];
b=[2 -3 -1 4 5 -8];r=1000;L=50;mu=0.01;
%construct input and desired output
x=-1+2*rand(r,1);d=filter(b,a,x);
%identify coefficients using basic lms method
N=length(x);
w=zeros(L+1,1);
theta=zeros(L+1,1);
e=zeros(size(x));q=x(:);
%find optimal weight vector
for k=1:N
if k<(L+1)
theta(1:k)=q(k:-1:1);
else
theta=q(k:-1:k-L);
end
e(k)=d(k)-w'*theta;
w=w+2*mu*e(k)*theta;
end
%plot squared error and compare magnitude responses
subplot(3,1,1)
t=1:min(500,r);
stem(t,e(t).^2,'filled','MarkerSize',1);axis([0 500 0 400]);
subplot(3,1,2)
fs=1;M=250;[H,f]=freqz(b,a,M,fs);
plot(f,abs(H));axis([0 0.5 0 70]);grid
subplot(3,1,3)
a1=[1,zeros(1,L)];[W,f]=freqz(w,a1,M,fs);plot(f,abs(W));
axis([0 0.5 0 70]);grid
figure
subplot(2,1,1)
n=0:L;
h=impz(b,a,L+1);
stem(n,h,'filled','MarkerSize',2)
subplot(2,1,2)
stem(n,w,'filled','MarkerSize',2)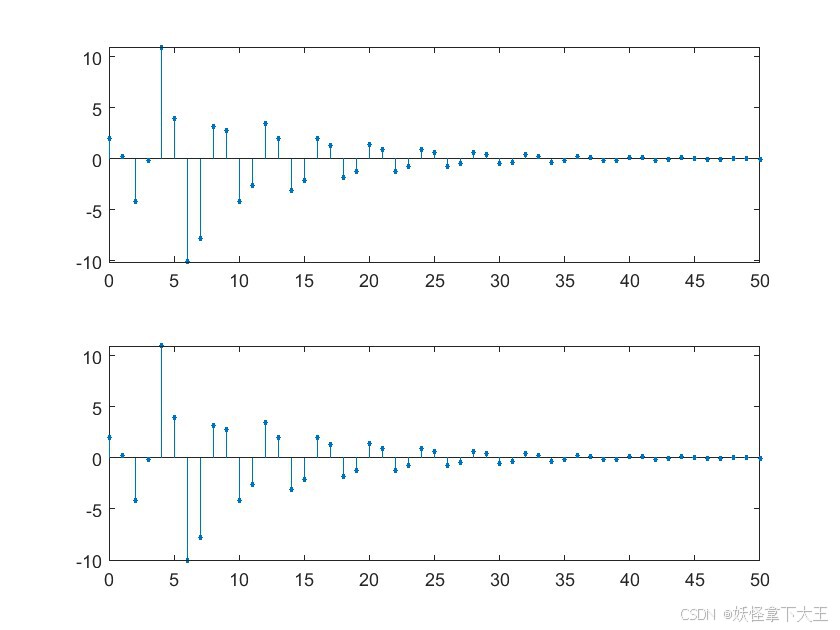
未知系统与自适应滤波器的冲击响应
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








