数据结构-浅谈线段树,树状数组[例题讲解学习]

🏆今日学习目标：
🍀学习算法-数据结构-线段树
✅创作者：贤鱼
⏰预计时间：30分钟
🎉个人主页：贤鱼的个人主页
🔥专栏系列：算法
🍁贤鱼的个人社区，欢迎你的加入 贤鱼摆烂团

🍁线段树

🍀线段树的用途

线段树可以实现单点修改,区间修改,区间查询等操作

为什么使用线段树

• 可以在$O({\log }_{2}n)$的时间复杂度内实现

🍀线段树结构

首先,线段树一定是一个二叉树

举个例子

a[6]={0,11,22,33,44,55};

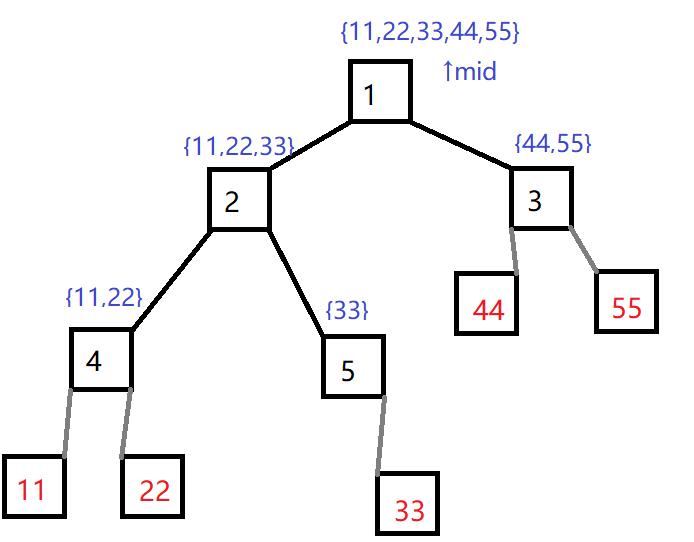
这是一个数组,那么这个数组构建的线段树是什么样呢(黑色编号(下文tr介绍),红色数值)

设置a[1]为根节点,a[2]和a[3]分别是左右儿子
那么是不是可以理解为
a[n]的孩子是a[n*2]和a[n*2+1]
我们设一个数组tr[i]储存编号为i所包含的数值
我们将数字编号1-n取一个中间数mid
将1~mid和mid+1~n分别分为左儿子和右儿子(注意mid不要重复)

🍀建树

上面介绍了线段树的基本构成,下面详细介绍如何建树

创建build函数

	void build(int o,int l,int r){//o当前节点,l,r就是上文分的mid, l~mid 和 mid+1~r
		if(l==r){
			cin>>tr[o].a;
			return;
		}
		build(o<<1,l,M);//o<<1代表o*2,但是左移速度快很多
		build(o<<1|1,M+1,r);//|1代表+1,速度比+1快
		pushup(o);//下文介绍
	}

唠唠pushup

	void pushup(int o){
		tr[o].a=tr[o<<1].a+tr[o<<1|1].a;//很简单啦,tr[i]=tr[i/2]+tr[i/2+1]递归啦
	}

🍀区间修改,单点修改

🍎懒惰标记

什么是懒惰标记(lazy)呢?

• 用来储存当前节点的状态(只有修改数值的时候会用到)

举个栗子(将2-3的每一个值增加3),我们就会将tr[2]和tr[3]的父亲的lazy记为3,这样子,如果tr[i].lazy有值,我们就往下推一位,将他的两个儿子lazy和值分别+3,然后清空当前lazy

注意,如果是往下推的lazy,必须累加,避免顶替之前的状态

为什么只往下推一位?
反正我记录lazy了,用到它了再推,可以节省时间麻~,反正多次推到同一个位置也是累加,不需要每次推到底(乘法另讲)

---

上文创建的tr,需要用结构体

	struct node{
		int a;
		int laz;//懒惰标记
	}tr[400040];

🍎加减

	void update(int o,int l,int r,int ql,int qr,int k){//o当前节点,lr是当前范围. ql,qr是修改范围,k是修改值
		if(ql<=l&&qr>=r){//包含就修改当前值并且记录lazy
			tr[o].a+=(r-l+1)*k;
			tr[o].laz+=k;
			return;
		}
		if(tr[o].laz)down(o,l,r);//这里down就是往下推,下文会有
		if(ql<=M) update(o<<1,l,M,ql,qr,k);
		if(qr>M) update(o<<1|1,M+1,r,ql,qr,k);//寻找合适范围,像不像二分~,原理如下图(千万不要if else!!!!!!!!!,可能存在两种都有的情况)
		pushup(o);

	}

假设修改2-4的值

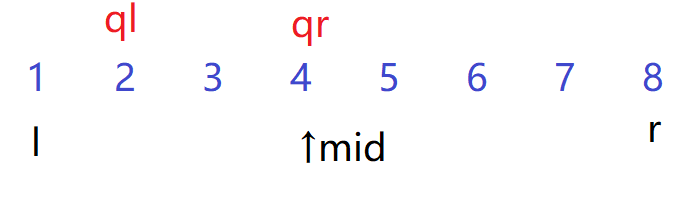
符合ql<=mid,不符合qr>mid

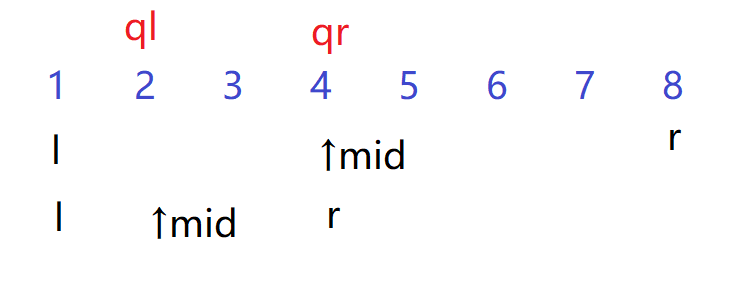
两个都符合

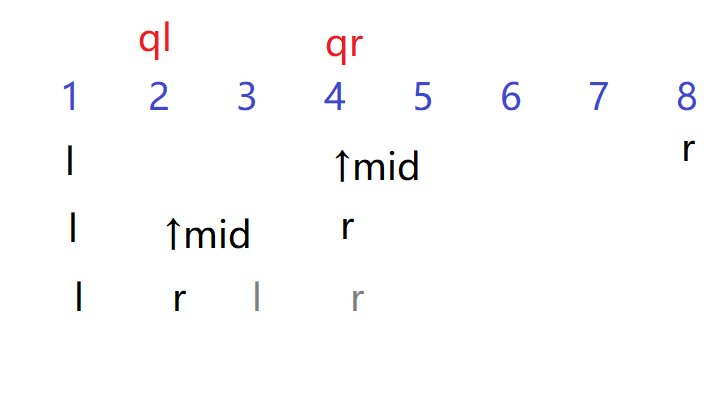
灰色lr区间找到

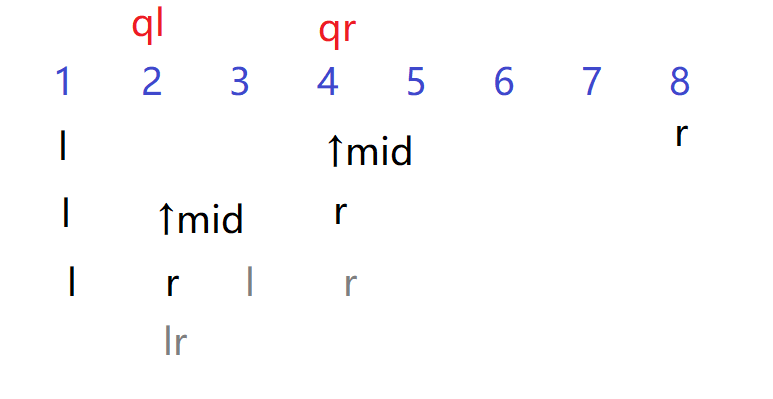
全部找到

	void down(int o,int l,int r){//按照父亲节点的lazy修改当前值
		tr[o<<1].a+=(M-l+1)*tr[o].laz;
		tr[o<<1|1].a+=(r-M)*tr[o].laz;
		tr[o<<1].laz+=tr[o].laz;
		tr[o<<1|1].laz+=tr[o].laz;
		tr[o].laz=0;//记得清零
	}

🍎乘

和+有亿点点区别,需要记录lazx,
tr[i]的lazx往下推的时候,需要用儿子的lazx*父亲的lazx
我乘一个数字,然后上面右往下乘了一个数字,是不是要互相乘
tr[i]的laz往下推的时候,需要用儿子的laz*父亲的lazx+父亲的laz
我加一个数字,是不是要先乘上面的数字(没有乘的时候lazx=1)再加上面推的数字
比较绕,但是读几遍应该可以理解

修改也是同理
当前的laz要乘修改的k
当前的lazx也要乘修改的k
乘法,那么未往下推的laz是不是也要相对应的乘

	void down(int x,int l,int r){
		if(tr[x].lazx==1&&tr[x].laz==0) return;
		tr[x<<1].lazx=tr[x].lazx*tr[x<<1].lazx;
		tr[x<<1|1].lazx=tr[x].lazx*tr[x<<1|1].lazx;
		tr[x<<1].laz=tr[x<<1].laz*tr[x].lazx+tr[x].laz;
		tr[x<<1|1].laz=tr[x<<1|1].laz*tr[x].lazx+tr[x].laz;
		tr[x<<1].a=tr[x<<1].a*tr[x].lazx+(M-l+1)*tr[x].laz;
		tr[x<<1|1].a=tr[x<<1|1].a*tr[x].lazx+(r-M)*tr[x].laz;
		tr[x].laz=0;
		tr[x].lazx=1;
	}
		void update1(int o,int l,int r,int ql,int qr,int k){
		if(ql<=l&&qr>=r){
			tr[o].a=tr[o].a*k;
			tr[o].laz=tr[o].laz*k;
			tr[o].lazx=tr[o].lazx*k;
			return;
		}
		down(o,l,r);
		if(ql<=M) update1(o<<1,l,M,ql,qr,k);
		if(qr>M) update1(o<<1|1,M+1,r,ql,qr,k);
		up(o);
	}

🍀区间查询

看懂了上面的,这个其实和他差不多.符合就返回值,不然继续寻找区间

	int query(int o,int l,int r,int ql,int qr){
		int ans=0;
		if(ql<=l&&qr>=r){
			return tr[o].a;
		}
		if(tr[o].laz)down(o,l,r);
		if(ql<=M) ans+=query(o<<1,l,M,ql,qr);
		if(qr>M) ans+=query(o<<1|1,M+1,r,ql,qr);
		return ans;
	}

🍀例题

🍌【模板】线段树 2

🍌题目描述

如题，已知一个数列，你需要进行下面三种操作：

• 将某区间每一个数乘上 $x$；
• 将某区间每一个数加上 $x$；
• 求出某区间每一个数的和。

🍌输入格式

第一行包含三个整数 $n,q,m$，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $q$ 行每行包含若干个整数，表示一个操作，具体如下：

操作 $1$： 格式：1 x y k 含义：将区间 $[x,y]$ 内每个数乘上 $k$

操作 $2$： 格式：2 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$

操作 $3$： 格式：3 x y 含义：输出区间 $[x,y]$ 内每个数的和对 $m$ 取模所得的结果

🍌输出格式

输出包含若干行整数，即为所有操作 $3$ 的结果。

🍌 样例 #1

🍌样例输入 #1

5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4

🍌样例输出 #1

17
2

🍌提示

【数据范围】

对于 $30\%$ 的数据：$n\le 8$，$q\le 10$。
对于 $70\%$ 的数据：$n \le 10^3 $，$q \le 10^4$。
对于 $100\%$ 的数据：$1\le n\le 10^5$，$1\le q\le 10^5$。

除样例外，$m=571373$。

（数据已经过加强 ^_）

样例说明：

故输出应为 $17$、$2$（$40\mathrm{mod}38=2$）。

🍌AC代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#include<queue>
using namespace std;
#define int long long
#define M ((l+r)/2)%m
int n,m,q;
namespace tr{
	struct node{
		int a;
		int laz;
		int lazx;
	}tr[4004000];
	void up(int x){
		tr[x].a=(tr[x<<1].a%m+tr[x<<1|1].a%m)%m;
	}
	
	void build(int o,int l,int r){
		tr[o].lazx=1;
		if(l==r){
			cin>>tr[o].a;
			return;
		}
		build(o<<1,l,M);
		build(o<<1|1,M+1,r);
		up(o);
	}
	
	void down(int x,int l,int r){//就是增加了一~大~堆~mod防止爆int
		if(tr[x].lazx==1&&tr[x].laz==0) return;
		tr[x<<1].lazx=1ll*(tr[x].lazx%m*tr[x<<1].lazx%m)%m;
		tr[x<<1|1].lazx=1ll*(tr[x].lazx%m*tr[x<<1|1].lazx%m)%m;
		tr[x<<1].laz=(1ll*(tr[x<<1].laz%m*tr[x].lazx%m)%m+tr[x].laz%m)%m;
		tr[x<<1|1].laz=(1ll*(tr[x<<1|1].laz%m*tr[x].lazx%m)%m+tr[x].laz%m)%m;
		tr[x<<1].a=(1ll*(tr[x<<1].a%m*tr[x].lazx%m)%m+(M-l+1)*tr[x].laz%m)%m;
		tr[x<<1|1].a=(1ll*(tr[x<<1|1].a%m*tr[x].lazx%m)%m+(r-M)*tr[x].laz%m)%m;
		tr[x].laz=0;
		tr[x].lazx=1;
	}
	
	void update(int o,int l,int r,int ql,int qr,int k){
		if(ql<=l&&qr>=r){
			tr[o].a+=(1ll*(r-l+1)*k%m)%m;
			tr[o].laz+=k%m;
			return ;
		}
		down(o,l,r);
		if(ql<=M) update(o<<1,l,M,ql,qr,k);
		if(qr>M) update(o<<1|1,M+1,r,ql,qr,k);
		up(o);
	}
	
	void update1(int o,int l,int r,int ql,int qr,int k){
		if(ql<=l&&qr>=r){
			tr[o].a=(tr[o].a%m*k%m)%m;
			tr[o].laz=(tr[o].laz%m*k%m)%m;
			tr[o].lazx=(tr[o].lazx%m*k%m)%m;
			return;
		}
		down(o,l,r);
		if(ql<=M) update1(o<<1,l,M,ql,qr,k);
		if(qr>M) update1(o<<1|1,M+1,r,ql,qr,k);
		up(o);
	}
	int query(int o,int l,int r,int ql,int qr){
		int ans=0;
		if(ql<=l&&qr>=r){
			return tr[o].a;
		}
		down(o,l,r);
		if(ql<=M) ans=(ans%m+query(o<<1,l,M,ql,qr)%m)%m;
		if(qr>M) ans=(ans%m+query(o<<1|1,M+1,r,ql,qr)%m)%m;
		return ans%m;
	}
}
using namespace tr;
signed main(){
	cin>>n>>q>>m;
	build(1,1,n);
	while(q!=0){
		q--;
		int w;
		cin>>w;
		int x,y,kk;
		if(w==1){
			cin>>x>>y>>kk;
			update1(1,1,n,x,y,kk);
		}else if(w==2){
			cin>>x>>y>>kk;
			update(1,1,n,x,y,kk);
		}else{
			cin>>x>>y;
			cout<<query(1,1,n,x,y)%m<<endl;
		}
	}
}

🍁树状数组

🍀树状数组和线段树关系

树状数组可以做的,线段树一定可以做,反之则不一定

🍀用途

树状数组可以支持单点修改和区间查询

🍀原理

如图是一个树状数组,a[i]代表当前包含内容的和

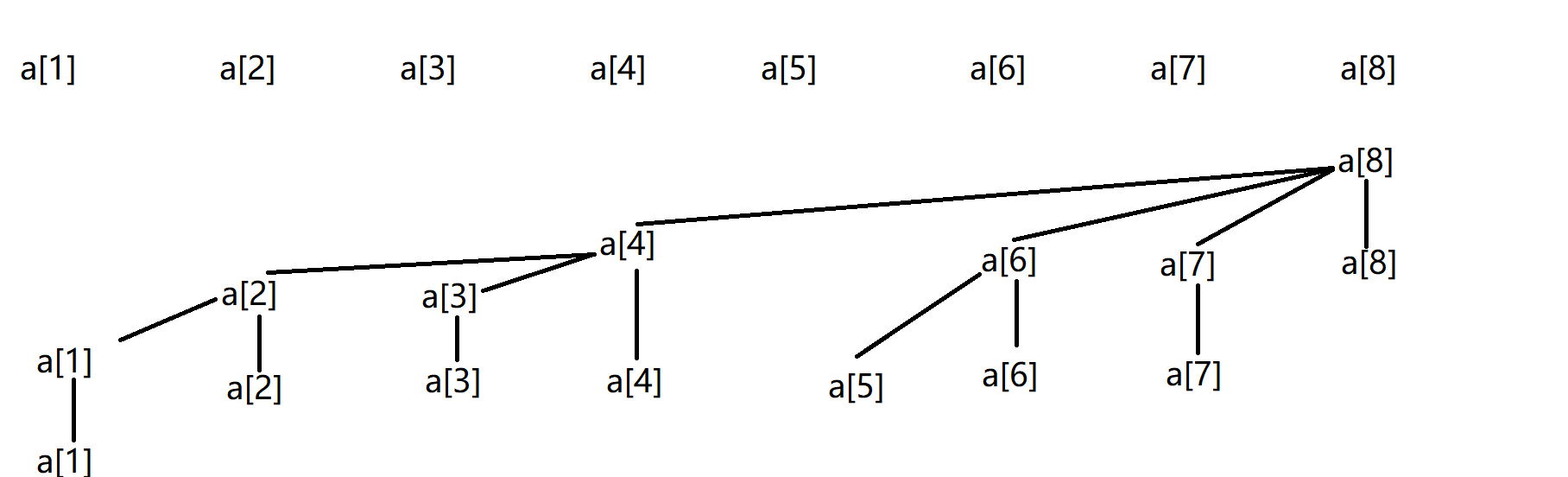
如何得到这个的呢? 看二进制

十进制	二进制
1	1
2	10
3	11
4	100

所以,从右往左,第一个1在哪里,当前就包含多少个内容(只算一层,不是算到底(例如4包含2,3,4,不算2,3包含的内容))

单点修改

首先我们需要知道一个操作lowbit,很简单,寻找二进制下右往左第一个1的

int lowbit(int x){
	return x&-x;
}

单点修改,同时输入也是这个

void add(int x, int k){
  while(x<=n){  
    a[x]=a[x]+k;
    x=x+lowbit(x);//一次性修改所有,从下一直修改到顶
  }
}

如上图如果1修改了,那么2,4,8的值都会改变

区间查询

int getsum(int x) { //和上面差不多,只不过这里求出来的和是1-n的,如果求l-r,需要getsum(r)-getsum(l-1)
  int ans=0;
  while(x>0){
    ans=ans+a[x];
    x=x-lowbit(x);
  }
  return ans;
}

例如求a[5]-a[7]的和

红色减去蓝色剩下的就是求的内容了

🍀例题

🍀AC代码

#include<cmath>
#include<cstdio>
#include<cstring>
#include<iostream>
#define int long long
using namespace std;
int n,m;
int a[10000005];
int l,r,k;
int lowbit(int x){
	return x&-x;
}
int getsum(int x) { 
  int ans=0;
  while(x>0){
    ans=ans+a[x];
    x=x-lowbit(x);
  }
  return ans;
}

void add(int x, int kk){
  while(x<=n){  
    a[x]=a[x]+kk;
    x=x+lowbit(x);
  }
}

signed main(){
	cin>>n>>m;
	int w;
	for(int i=1;i<=n;i++)
		cin>>w,add(i,w);
	while(m!=0){
		m--;
		int x;
		cin>>x;
		if(x==1){
			cin>>l>>k;
			add(l,k);
		}else{
			cin>>l>>r;
			cout<<getsum(r)-getsum(l-1)<<endl;
		}
	}
}

🍁结束语

如果对您有帮助的话,点个赞支持一下贤鱼吧🏆