快速排序（Hare版本）

1.原理

每一趟排序，先选出key，将比key小的值排左边，比key大的值排右边，然后在子区间上重复此操作。

如图： 定义key为第一个数，定义L和R两个值记录下标，R先走找到比key小的值停下，然后L再走找到比key大的值停下，然后交换L和R的值，重复过程直到L与R相遇，将key交换到相遇位置处。使得数组中的值：{小于等于key的值} key {大于等于key的值}。

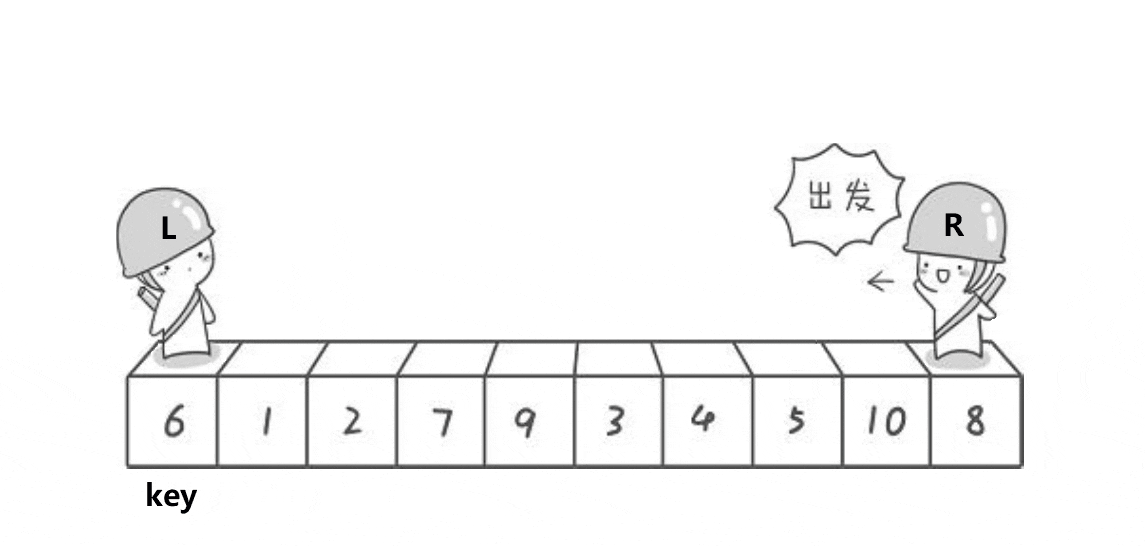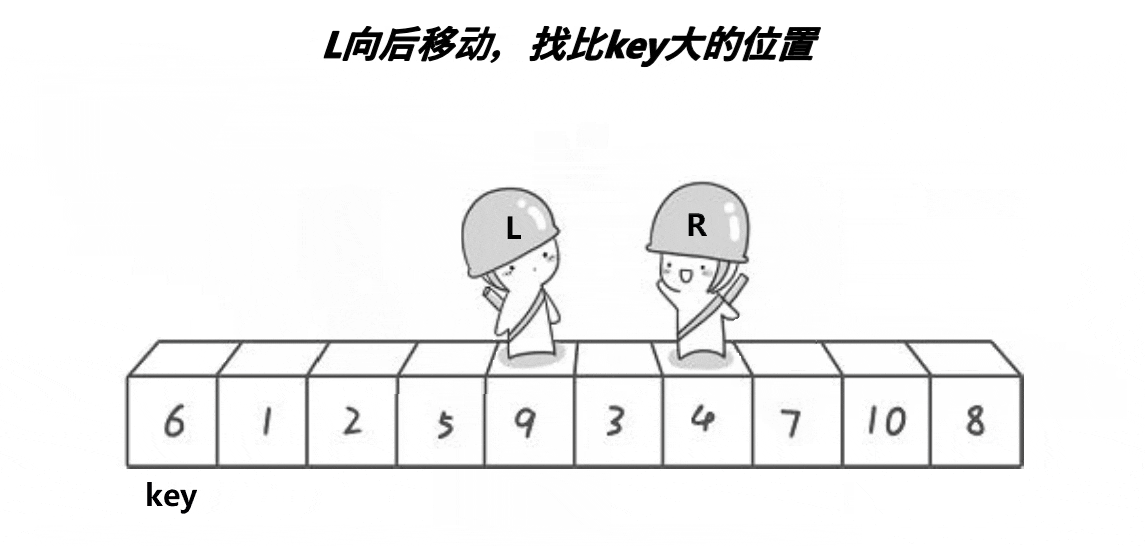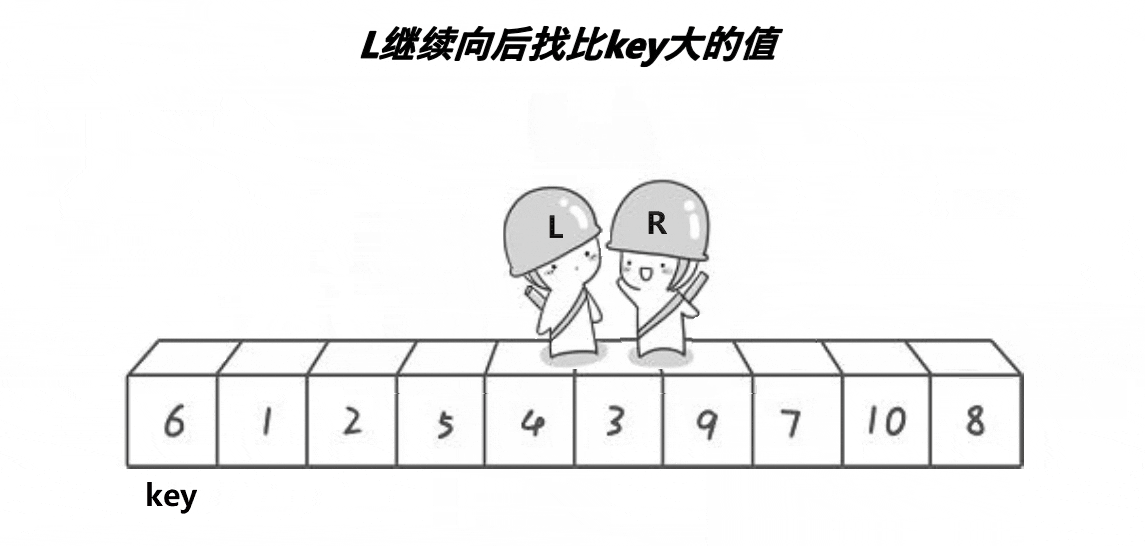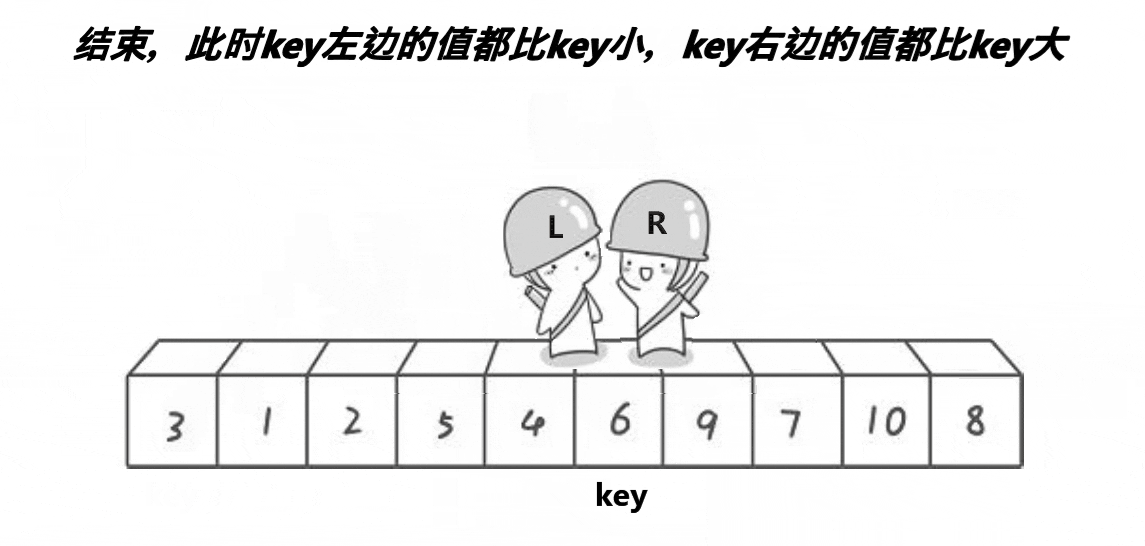
2.代码实现（递归版）

2.1首先写下单趟排序。

为什么要R先走呢？因为R先走在比key小的位置停下来了，L没有找到比key大的元素就会和R相遇，相遇位置R停下的位置是比key小的位置。

//begain、end分别为排序子区间的第一个元素的下标、最后一个元素的下标
int left = begain, right = end, keyi = begain;

while (left < right)
{
	//right先走确保最后left和right相遇时元素必定小于keyi
	while (left < right && a[right] >= a[keyi])
	{
		right--;
	}
	while (left < right && a[left] <= a[keyi])
	{
		left++;
	}
	Swap(&a[left], &a[right]);
}
//使最后keyi左边的元素都小于它，右边的元素都大于它
Swap(&a[right], &a[keyi]);

2.2分为子问题

当单趟排完之后，我们就继续排[begain,keyi-1] 和 [keyi+1,end]两个子区间。我们可以用递归实现，那么最小子问题（返回的条件）是什么呢？即传入的begain >= end时传入的区间的元素数小于一个时返回。

if (begain >= end)
{
	return;
}

2.3参考代码

//快排
//Hoare版本
void QuickSort(int* a, int begain, int end) {
	
	if (begain >= end)
	{
		return;
	}
	int left = begain, right = end, keyi = begain;

	while (left < right)
	{
		//right先走确保最后left和right相遇时元素必定小于keyi
		while (left < right && a[right] >= a[keyi])
		{
			right--;
		}
		while (left < right && a[left] <= a[keyi])
		{
			left++;
		}
		Swap(&a[left], &a[right]);
	}
	//使最后keyi左边的元素都小于它，右边的元素都大于它
	Swap(&a[right], &a[keyi]);

	keyi = left;
	//运用搜索二叉树的思想，递归实现
	//[begain,keyi-1] keyi [keyi+1,end]
	QuickSort(a, begain, keyi - 1);//keyi的左区间
	QuickSort(a, keyi+1, end);//keyi的右区间
}

3.拓展

3.1前后指针法快排

//快排快慢指针法
void QuickSort2(int* a, int begain, int end) {

	if (begain >= end)
	{
		return;
	}
	int prev = begain, cur = begain + 1, keyi = begain;

	while (cur <= end)
	{
		//a[cur] > a[keyi]时只有cur向前走，使得prev与cur之间都是比 a[keyi]大的元素
		if (a[cur] > a[keyi])
		{
			cur++;
		}
		//a[cur] > a[keyi]时，prev先++，若++后的prev!= cur则Swap，使得prev与cur之间都是比 a[keyi]大的元素
		else
		{
			if (++prev != cur)
			{
				Swap(&a[prev], &a[cur]);
			}
			cur++;
		}
		
	}
	//使最后keyi左边的元素都小于它，右边的元素都大于它
	Swap(&a[prev], &a[keyi]);

	//[begain,keyi-1] keyi [keyi+1,end]
	//运用搜索二叉树的思想，递归实现
	QuickSort2(a, begain, prev - 1);//keyi的左区间
	QuickSort2(a, prev + 1, end);//keyi的右区间
}

3.2非递归版本快排

要模拟递归，最重要的是储存下一次排序的区间，然后取用直到所以区间都排完结束。

//非递归法快排
void QuickSortNonR(int* a, int begain, int end)
{
	//用栈存储每趟排序的区间
	ST stack;
	STInit(&stack);

	//先取begain，后取end，故压栈时要先压end，再压begain
	STPush(&stack, end);
	STPush(&stack, begain);

	//若栈存在数据说明没有将所有区排序完
	while (!STEmpty(&stack))
	{
		//取数据
		int left = STTop(&stack);
		STPop(&stack);
		int right = STTop(&stack);
		STPop(&stack);

		//储存排序区间，便于将子排序区间压栈
		int begain = left;
		int end = right;


		int keyi = left;
		while (left < right)
		{

			while (left < right && a[right] >= a[keyi])
			{
				//右指针向左移动，找到小于a[keyi]的数据停下
				right--;
			}
			while (left < right && a[left] <= a[keyi])
			{
				//左指针向右移动，找到大于a[keyi]的数据停下
				left++;
			}
			//此时a[right] >= a[keyi]，a[left] <= a[keyi]，交换可助推最后keyi左边的元素都小于它，右边的元素都大于它
			Swap(&a[left], &a[right]);
		}
		//左右指针相遇后交换a[left], a[keyi]，使keyi左边的元素都小于它，右边的元素都大于它
		Swap(&a[left], &a[keyi]);

		//[begain,keyi-1] keyi [keyi+1,end]
		if (begain < keyi - 1)
		{
			//先取begain，后取end，故压栈时要先压end，再压begain
			STPush(&stack, keyi - 1);
			STPush(&stack, begain);
		}
		if (keyi + 1 < end)
		{
			//先取begain，后取end，故压栈时要先压end，再压begain
			STPush(&stack, end);
			STPush(&stack, keyi + 1);
		}

	}


}