基于前馈神经网络的姓氏分类

最新推荐文章于 2024-06-28 12:37:06 发布

m0_67461772

最新推荐文章于 2024-06-28 12:37:06 发布

阅读量988

点赞数 14

文章标签： python 人工智能 nlp

本文链接：https://blog.csdn.net/m0_67461772/article/details/139566279

版权

1、引言

1.1 背景介绍

神经网络在近年来的机器学习和深度学习领域中得到了广泛应用，尤其在文本分类任务中表现出了显著的优势。文本分类是自然语言处理（Natural Language Processing，NLP）中的一项基础任务，旨在将文本片段（如句子、段落或文档）分配到一个或多个类别中。常见的文本分类任务包括情感分析、垃圾邮件检测、主题分类等。

神经网络在文本分类中的应用主要得益于其强大的特征提取和模式识别能力。传统的文本分类方法依赖于手工设计的特征，而神经网络，特别是深度神经网络，可以通过自动学习数据中的复杂模式，从而提高分类性能。以下是几种常用的神经网络模型在文本分类中的应用：

多层感知器（Multilayer Perceptron，MLP）：MLP是一种前馈神经网络，具有输入层、隐藏层和输出层。尽管MLP在处理线性可分问题上表现良好，但其在处理复杂的非线性问题时存在局限性，特别是当输入数据具有时序或空间关系时。
卷积神经网络（Convolutional Neural Network，CNN）：CNN通过卷积层和池化层，能够有效提取输入数据中的局部特征。CNN最初用于图像处理，但在文本分类任务中也表现出色，尤其在捕捉局部n-gram特征方面。
递归神经网络（Recurrent Neural Network，RNN）：RNN特别适用于处理序列数据，如文本和时间序列数据。RNN通过其循环结构，可以捕捉输入序列中的长短期依赖关系。然而，RNN在处理长序列时可能会遇到梯度消失或梯度爆炸问题。
长短期记忆网络（Long Short-Term Memory，LSTM）：LSTM是RNN的一种变体，通过引入门控机制，可以更好地捕捉长时间依赖关系，解决了标准RNN在处理长序列时的不足。

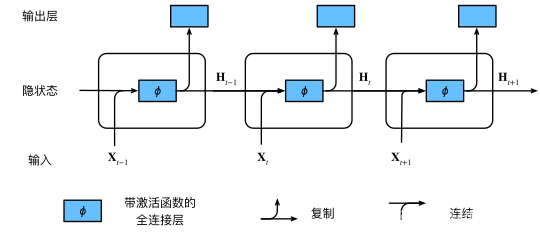
以上图片来自：《动手学深度学习》 — 动手学深度学习 2.0.0 documentation (d2l.ai)

在姓氏分类任务中，神经网络被用来根据给定的姓氏预测其所属的国籍。姓氏分类具有一定的实际应用价值，如在社交媒体分析、市场研究、用户个性化推荐等领域。姓氏分类的挑战在于姓氏的多样性和变异性，以及不同国籍之间的重叠特征。因此，利用神经网络的强大学习能力，可以在此任务中获得良好的分类效果。

1.2 实验目的

本实验的主要目标是比较多层感知器（MLP）和卷积神经网络（CNN）在姓氏分类任务中的表现。具体目标如下：

构建并训练多层感知器模型：通过MLP模型对姓氏数据进行分类，了解其在多类分类任务中的表现。MLP模型的设计将基于前馈神经网络，包含一个或多个隐藏层和一个输出层。
构建并训练卷积神经网络模型：通过CNN模型对姓氏数据进行分类，探索其在捕捉姓氏局部特征方面的优势。CNN模型将包含卷积层、池化层和全连接层，以提取姓氏中的关键模式。
性能比较：通过实验对比MLP和CNN两种模型在姓氏分类任务中的准确率、训练时间和模型复杂度。性能比较将帮助我们理解不同神经网络结构在处理文本分类任务时的优劣。
探讨Dropout对模型性能的影响：在模型训练过程中引入Dropout技术，探讨其对防止过拟合和提高模型泛化能力的影响。

通过以上实验步骤，我们希望能够系统地了解不同神经网络模型在姓氏分类任务中的表现，为后续的模型优化和应用提供依据。

2、感知器与多层感知器

2.1 感知器简介

感知器（Perceptron）是神经网络中最基础的构建单元之一，也是最早提出的人工神经网络模型之一。它由Frank Rosenblatt于1958年提出，旨在模拟生物神经元的基本功能。感知器的基本结构和工作原理如下：

基本结构：

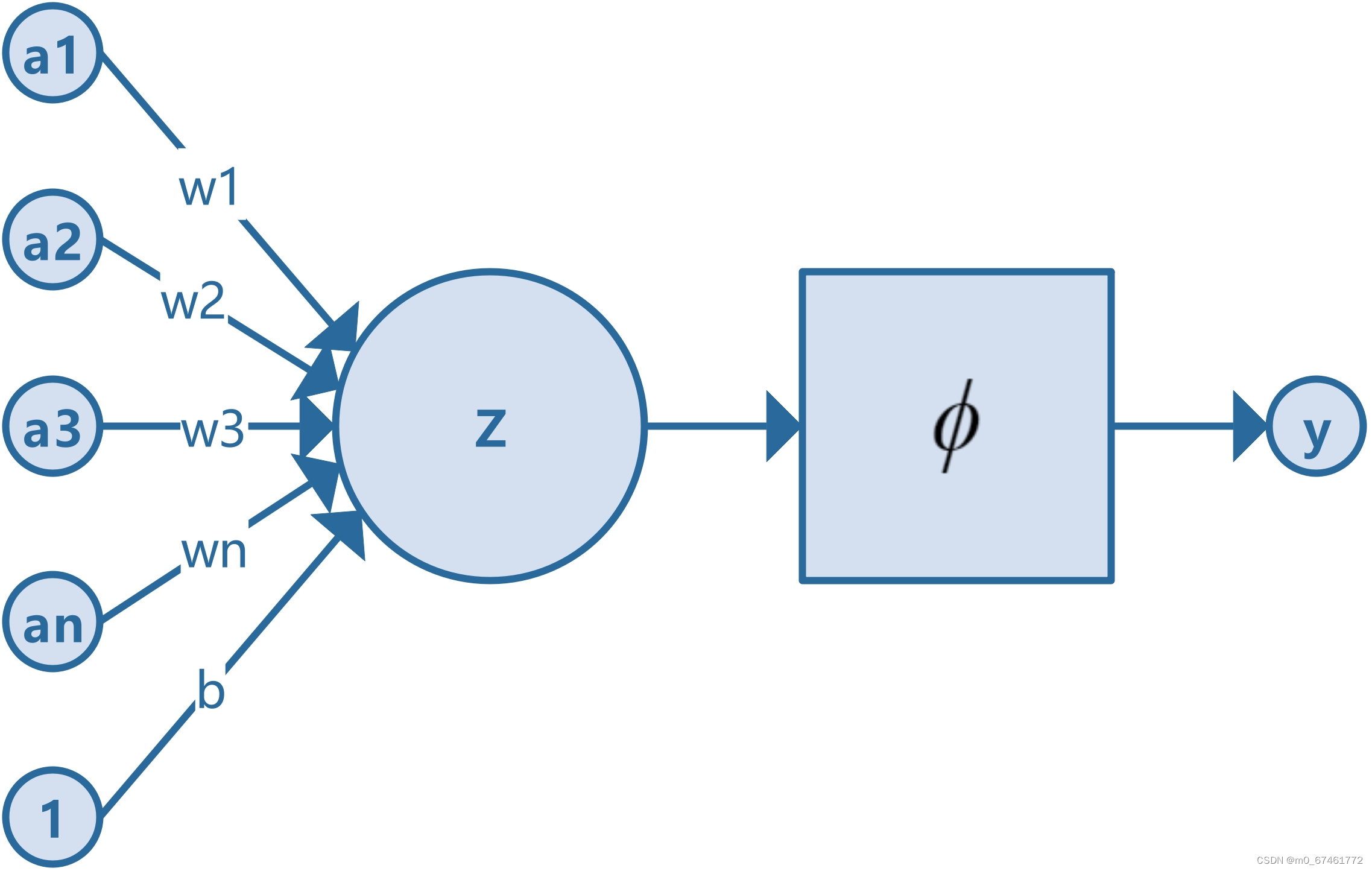
一个典型的感知器由以下几个部分组成：

输入层（Input Layer）：包含多个输入节点，每个节点代表一个输入特征。输入层接受外部输入信号，可以是文本数据、图像数据或其他类型的数据。
权重（Weights）：每个输入节点都有一个对应的权重，这些权重表示输入信号的重要程度。在训练过程中，权重会不断调整，以便模型能够更好地学习数据中的模式。
加权和（Weighted Sum）：感知器对输入信号进行加权，并计算所有加权输入的总和。
偏置（Bias）：偏置是一个额外的可调参数，用于调整模型的输出。偏置可以看作是输入信号总和的一个固定补充值，帮助模型更好地拟合数据。
激活函数（Activation Function）：感知器通过激活函数对加权和进行处理，激活函数将加权和转换为输出信号。常见的激活函数包括阶跃函数、Sigmoid函数和ReLU函数等。

工作原理：

感知器的工作原理可以概括为以下几个步骤：

接收输入：感知器接收多个输入信号，每个信号用 $x_i$ 表示，其中 $i$ 表示第 $i$ 个输入特征。
加权输入：感知器将每个输入信号与对应的权重 $\omega_{i}$ 相乘，得到加权输入 $\omega_i\cdot x_i$ 。
计算加权和：感知器对所有加权输入进行求和，并加上偏置 $b$ ，计算出加权和 $z$ ：

$\displaystyle z=\sum_{i=1}^{n}\omega_{i}\cdot x_i+b$

4. 激活函数：感知器将加权和 $z$ 输入到激活函数中，得到最终输出 $y$ :

$y=\phi(z)$

其中， $\phi$ 为激活函数。

5. 输出信号：激活函数的输出 $y$ 就是感知器的输出信号，用于下一层神经元的输入或直接作为模型的预测结果。

示例代码：

以下是一个简单的二分类感知器的示例代码，使用Python和PyTorch实现，该感知器用于判断输入数据是否属于某一类别：

1. 定义感知器模型：

class Perceptron(nn.Module):
    def __init__(self, input_dim):
        super(Perceptron, self).__init__()
        self.fc = nn.Linear(input_dim, 1)  # 全连接层

    def forward(self, x):
        z = self.fc(x)  # 计算加权和
        y = torch.sigmoid(z)  # 使用Sigmoid激活函数
        return y

这里定义了一个简单的感知器模型，包含一个全连接层和一个Sigmoid激活函数。

2. 初始化模型、损失函数和优化器：

input_dim = 2
model = Perceptron(input_dim)
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01)

初始化感知器模型，使用二元交叉熵损失函数和随机梯度下降优化器。

3. 生成示例数据：

data = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
labels = torch.tensor([[0.0], [1.0], [1.0], [0.0]])  # XOR问题

生成一些示例数据，这里使用XOR问题作为示例。

4. 训练模型：

num_epochs = 1000
for epoch in range(num_epochs):
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

    loss_values.append(loss.item())  # 记录损失值

    if (epoch + 1) % 100 == 0:
        print(f'Epoch [{epoch + 1}/{num_epochs}], Loss: {loss.item():.4f}')

5. 绘制损失曲线：

plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.plot(range(num_epochs), loss_values, label='Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss Curve')
plt.legend()

6. 测试模型并绘制分类结果：

with torch.no_grad():
    test_data = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
    predictions = model(test_data)
    predicted_labels = predictions.round()
    
    # 提取预测结果
    test_data = test_data.numpy()
    predicted_labels = predicted_labels.numpy()
    
    # 绘制分类结果
    plt.subplot(1, 2, 2)
    for i, (x, y) in enumerate(zip(test_data, predicted_labels)):
        if y == 0:
            plt.scatter(x[0], x[1], color='red', marker='x', label='Class 0' if i == 0 else "")
        else:
            plt.scatter(x[0], x[1], color='blue', marker='o', label='Class 1' if i == 1 else "")
    
    plt.title('Classification Results')
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.grid(True)

plt.tight_layout()
plt.show()

结果：

2.2 感知器的局限性

感知器的一个主要局限性是它只能解决线性可分的问题。也就是说，如果数据集中的各个类别可以通过一条直线（在二维情况下）或一个超平面（在更高维情况下）来分割，那么感知器可以很好地处理。然而，对于非线性可分的问题，感知器则无能为力。例如，经典的XOR（异或）问题就是一个典型的非线性可分问题，感知器无法解决这个问题。这也就是为什么上文的代码运行结果是错误的。

为了解决这些局限性，研究人员提出了多层感知器（MLP），通过增加隐藏层和使用非线性激活函数，使其能够处理复杂的非线性问题。

2.3 多层感知器的概念与优势

多层感知器是一种前馈神经网络，由输入层、一个或多个隐藏层和输出层组成。每一层中的神经元与前一层的神经元完全连接，通过加权和偏置的线性组合，经过非线性激活函数的作用，将输入映射到输出。

结构概述：

输入层：接收外部输入数据，输入层的每个神经元代表一个输入特征。
隐藏层：位于输入层和输出层之间，可以有一个或多个隐藏层。隐藏层中的神经元对输入数据进行复杂的特征提取和非线性变换。
输出层：将隐藏层的输出转换为最终的预测结果。

公式表示：

假设输入向量为 $\mathbf{x}=[x_1,x_2,...,x_n]$ ，权重矩阵为 $\mathbf{W}$ ，偏置向量为 $\mathbf{b}$ ，则第 $l$ 层的输入 $\mathbf{a}^l$ 可以表示为：

1. 输入层到隐藏层的变换：

$\mathbf{z}^1=\mathbf{W}^1x+\mathbf{b}^1$

$\mathbf{a}^1=\phi (\mathbf{z}^1)$

其中， $\phi$ 是激活函数，如ReLU，Sigmoid等。

2. 隐藏层之间的变换（假设有 $L-1$ 个隐藏层）：

$\mathbf{z}^l = \mathbf{W}^l \mathbf{a}^{l-1} + \mathbf{b}^l \quad \text{for} \quad l = 2, \ldots, L-1$

$\mathbf{a}^l = \phi(\mathbf{z}^l)$

3. 隐藏层到输出层的变换:

$\mathbf{z}^L = \mathbf{W}^L \mathbf{a}^{L-1} + \mathbf{b}^L$

$\mathbf{a}^L=\phi (\mathbf{z}^L)$

其中：

$\mathbf{W}^l$ 是第 $l$ 层的权重矩阵。
$\mathbf{b^l}$ 是第 $l$ 层的偏置向量。

示例代码：多层感知器解决XOR问题

import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt

# 定义多层感知器模型
class MLP(nn.Module):
    def __init__(self, input_dim, hidden_dim, output_dim):
        super(MLP, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)
        self.fc2 = nn.Linear(hidden_dim, output_dim)

    def forward(self, x):
        z1 = self.fc1(x)
        a1 = torch.relu(z1)  # 使用ReLU激活函数
        z2 = self.fc2(a1)
        y = torch.sigmoid(z2)  # 使用Sigmoid激活函数
        return y

# 初始化模型、损失函数和优化器
input_dim = 2
hidden_dim = 4
output_dim = 1
model = MLP(input_dim, hidden_dim, output_dim)
criterion = nn.BCELoss()  # 二元交叉熵损失
optimizer = optim.SGD(model.parameters(), lr=0.01)

# 生成XOR示例数据
data = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
labels = torch.tensor([[0.0], [1.0], [1.0], [0.0]])  # XOR问题

# 训练模型
num_epochs = 1000
for epoch in range(num_epochs):
    optimizer.zero_grad()
    outputs = model(data)
    loss = criterion(outputs, labels)
    loss.backward()
    optimizer.step()

# 测试模型并绘制分类结果
with torch.no_grad():
    test_data = torch.tensor([[0.0, 0.0], [0.0, 1.0], [1.0, 0.0], [1.0, 1.0]])
    predictions = model(test_data)
    predicted_labels = predictions.round()
    
    # 提取预测结果
    test_data = test_data.numpy()
    predicted_labels = predicted_labels.numpy()
    
    # 绘制分类结果
    plt.figure(figsize=(6, 6))
    for i, (x, y) in enumerate(zip(test_data, predicted_labels)):
        if y == 0:
            plt.scatter(x[0], x[1], color='red', marker='x', label='Class 0' if i == 0 else "")
        else:
            plt.scatter(x[0], x[1], color='blue', marker='o', label='Class 1' if i == 1 else "")
    
    plt.title('MLP XOR Classification Results')
    plt.xlabel('Feature 1')
    plt.ylabel('Feature 2')
    plt.legend()
    plt.grid(True)
    plt.show()

结果：

可以看出，此时的结果是正确的。

多层感知器的优势：

1. 处理非线性问题：

多层感知器通过引入隐藏层和非线性激活函数，能够处理复杂的非线性问题。与单层感知器相比，MLP可以对数据进行更深层次的特征提取和变换。也就是说：MLP实现了线性到非线性的转化。

2. 通用性强（通用近似原理）：

多层感知机可以通过隐藏神经元，捕捉到输入之间复杂的相互作用，这些神经元依赖于每个输入的值。我们可以很容易地设计隐藏节点来执行任意计算。例如，在一对输入上进行基本逻辑操作，多层感知机是通用近似器。即使是网络只有一个隐藏层，给定足够的神经元和正确的权重，我们可以对任意函数建模，尽管实际中学习该函数是很困难的。

而且，虽然一个单隐层网络能学习任何函数，但并不意味着我们应该尝试使用单隐藏层网络来解决所有问题。事实上，通过使用更深（而不是更广）的网络，我们可以更容易地逼近许多函数。

3、实验环境与准备

3.1 实验所需环境

Python 3.6.7
PyCharm Community Edition 2022.2.2

3.2 数据集介绍

在本实验中，使用了一个包含姓氏及其对应国籍的数据集。该数据集旨在通过姓氏来预测其所属的国籍。数据集包含多种国籍的姓氏，涉及的国家包括英语国家、阿拉伯国家、俄语国家、日语国家等。

具体来说：姓氏数据集，它收集了来自18个不同国家的10,000个姓氏，这些姓氏是从互联网上不同的姓名来源收集的。该数据集具有一些使其有趣的属性。第一个性质是它是相当不平衡的。排名前三的课程占数据的60%以上:27%是英语，21%是俄语，14%是阿拉伯语。剩下的15个民族的频率也在下降——这也是语言特有的特性。第二个特点是，在国籍和姓氏正字法(拼写)之间有一种有效和直观的关系。有些拼写变体与原籍国联系非常紧密(比如“O ‘Neill”、“Antonopoulos”、“Nagasawa”或“Zhu”)。

为了创建最终的数据集，我执行了几个数据集修改操作。第一个目的是减少这种不平衡——原始数据集中70%以上是俄文，这可能是由于抽样偏差或俄文姓氏的增多。为此，通过选择标记为俄语的姓氏的随机子集对这个过度代表的类进行子样本。接下来，根据国籍对数据集进行分组，并将数据集分为三个部分:70%到训练数据集，15%到验证数据集，最后15%到测试数据集，以便跨这些部分的类标签分布具有可比性。

3.3 工具介绍

在本实验中，我主要使用了以下两个工具：Jupyter Notebook和PyTorch。

Jupyter Notebook

Jupyter Notebook 是一种交互式的计算环境，能够让用户在一个文档中创建和共享包含代码、方程式、可视化和文本的文档。它特别适合用于数据清洗和转换、数值模拟、统计建模、机器学习等工作。

特点：

交互性：允许逐步执行代码段，并立即查看结果，便于调试和试验。
可视化：支持内嵌图表，能够直观展示数据和分析结果。
可重现性：整个实验过程都记录在一个文档中，方便他人理解和复现。
多语言支持：不仅支持Python，还支持R、Julia等多种编程语言。

使用场景：

数据分析与可视化：通过集成的Matplotlib、Seaborn等库，Jupyter Notebook可以方便地进行数据可视化和分析。
机器学习实验：适合快速构建和测试机器学习模型，调试代码，调整参数。
教育和演示：教学过程中可以一步步展示代码和结果，便于学生理解和学习。

PyTorch

PyTorch 是一个开源的深度学习框架，由Facebook's AI Research lab（FAIR）开发。它提供了灵活、高效的张量计算和自动求导功能，广泛应用于研究和生产中。

特点：

动态计算图：PyTorch采用动态计算图（Dynamic Computational Graph），允许在运行时改变网络结构，使调试和模型设计更加灵活和直观。
强大的张量计算：提供类似于NumPy的张量计算功能，并且可以在GPU上高效运行，极大地提高了计算速度。
自动求导：通过Autograd模块，PyTorch可以自动计算梯度，简化了反向传播的实现。
模块化设计：拥有丰富的神经网络模块（如nn.Module），方便用户构建和扩展模型。

使用场景：

深度学习研究：灵活的动态计算图和强大的张量计算能力，使PyTorch非常适合进行前沿的深度学习研究。
工业应用：许多企业在生产环境中使用PyTorch进行模型训练和部署，得益于其高效的计算性能和易用性。
教学与学习：由于其简洁的API和良好的文档，PyTorch也是学习深度学习的理想工具。

基本操作：

张量操作：类似于NumPy的多维数组，支持各种数学运算。
模型定义：通过继承nn.Module类定义神经网络模型。
训练与优化：提供优化器模块（如SGD, Adam），便于实现梯度下降和模型训练。

4、实验步骤

4.1 数据预处理

数据加载：

# SurnameDataset 类
class SurnameDataset(Dataset):
    def __init__(self, surname_df, vectorizer):
        """
        用一个数据框和一个向量化器初始化数据集。
        
        参数:
            surname_df (pd.DataFrame): 包含数据的数据框。
            vectorizer (SurnameVectorizer): SurnameVectorizer 类的一个实例。
        """
        self.surname_df = surname_df
        self._vectorizer = vectorizer

        # 将数据框分为训练集、验证集和测试集
        self.train_df = self.surname_df[self.surname_df.split == 'train']
        self.train_size = len(self.train_df)

        self.val_df = self.surname_df[self.surname_df.split == 'val']
        self.validation_size = len(self.val_df)

        self.test_df = self.surname_df[self.surname_df.split == 'test']
        self.test_size = len(self.test_df)

        self._target_df = self.train_df  # 默认目标数据框为训练集

        # 计算类别权重以处理类别不平衡
        class_counts = self.surname_df['nationality'].value_counts().to_dict()
        sorted_counts = sorted(class_counts.items())
        self.class_weights = 1.0 / torch.tensor([count for _, count in sorted_counts], dtype=torch.float32)

    @classmethod
    def load_dataset_and_make_vectorizer(cls, surname_csv):
        """
        从 CSV 文件加载数据集并从训练数据中创建一个向量化器。
        
        参数:
            surname_csv (str): 包含数据的 CSV 文件路径。
        
        返回:
            SurnameDataset: SurnameDataset 类的一个实例。
        """
        surname_df = pd.read_csv(surname_csv)
        # 随机分配 splits (train, validation, test)
        np.random.seed(1337)
        mask = np.random.rand(len(surname_df))
        surname_df['split'] = np.where(mask <= 0.7, 'train',
                                       np.where(mask <= 0.85, 'val', 'test'))
        
        train_df = surname_df[surname_df.split == 'train']
        vectorizer = SurnameVectorizer.from_dataframe(train_df)
        return cls(surname_df, vectorizer)

    def get_vectorizer(self):
        """
        获取数据集使用的向量化器。
        
        返回:
            SurnameVectorizer: 向量化器实例。
        """
        return self._vectorizer

    def set_split(self, split="train"):
        """
        将目标数据框设置为指定的 split。
        
        参数:
            split (str): 可以是 'train', 'val' 或 'test'。
        """
        if split == "train":
            self._target_df = self.train_df
        elif split == "val":
            self._target_df = self.val_df
        elif split == "test":
            self._target_df = self.test_df
        else:
            raise ValueError("split 应该是 train, val 或 test 之一")

    def __len__(self):
        """
        返回当前目标数据框中的样本数量。
        
        返回:
            int: 样本数量。
        """
        return len(self._target_df)

    def __getitem__(self, index):
        """
        获取指定索引处的数据集样本。
        
        参数:
            index (int): 要检索的样本索引。
        
        返回:
            dict: 包含向量化的姓氏和国籍索引的字典。
        """
        row = self._target_df.iloc[index]
        surname_vector = self._vectorizer.vectorize(row.surname)
        nationality_index = self._vectorizer.nationality_vocab.lookup_token(row.nationality)

        return {'x_surname': surname_vector, 'y_nationality': nationality_index}

为了使用字符对姓氏进行分类，我们使用词汇表、向量化器和DataLoader将姓氏字符串转换为向量化的minibatches。数据不是通过将字令牌映射到整数来向量化的，而是通过将字符映射到整数来向量化的。

THE VOCABULARY CLASS

本例中使用的词汇类将的单词映射到对应的整数。简要概述一下，词汇表是两个Python字典的协调，这两个字典在令牌(在本例中是字符)和整数之间形成一个双射;也就是说，第一个字典将字符映射到整数索引，第二个字典将整数索引映射到字符。add_token方法用于向词汇表中添加新的令牌，lookup_token方法用于检索索引，lookup_index方法用于检索给定索引的令牌(在推断阶段很有用)。我使用的是one-hot词汇表，不计算字符出现的频率，只对频繁出现的条目进行限制。这主要是因为数据集很小，而且大多数字符足够频繁。

class Vocabulary:
    def __init__(self, add_unk=True, unk_token="<UNK>"):
        """
        初始化词汇表。

        参数:
            add_unk (bool): 是否添加一个未知的标记。
            unk_token (str): 未知标记的字符串表示。
        """
        self._token_to_idx = {}  # 字符串到索引的映射
        self._idx_to_token = []  # 索引到字符串的映射
        self._add_unk = add_unk  # 是否添加未知标记
        self._unk_token = unk_token  # 未知标记的字符串

        if add_unk:
            self.unk_index = self.add_token(unk_token)  # 添加未知标记并获取其索引

    def add_token(self, token):
        """
        向词汇表中添加一个新标记。

        参数:
            token (str): 要添加的标记。

        返回:
            int: 标记的索引。
        """
        if token in self._token_to_idx:
            index = self._token_to_idx[token]
        else:
            index = len(self._idx_to_token)  # 新标记的索引为当前索引列表的长度
            self._token_to_idx[token] = index  # 添加标记到索引的映射
            self._idx_to_token.append(token)  # 添加标记到索引列表
        return index

    def lookup_token(self, token):
        """
        查找标记的索引。

        参数:
            token (str): 要查找的标记。

        返回:
            int: 标记的索引，如果未找到则返回未知标记的索引（如果已添加）。
        """
        if self._add_unk:
            return self._token_to_idx.get(token, self.unk_index)  # 返回标记的索引，或未知标记的索引
        else:
            return self._token_to_idx[token]  # 返回标记的索引（不处理未找到的情况）

    def __len__(self):
        """
        返回词汇表中标记的数量。

        返回:
            int: 标记的数量。
        """
        return len(self._idx_to_token)  # 返回索引列表的长度

THE SURNAMEVECTORIZER

虽然词汇表将单个令牌(字符)转换为整数，但SurnameVectorizer负责应用词汇表并将姓氏转换为向量。实例化需要注意的是字符串没有在空格上分割。姓氏是字符的序列，每个字符在我们的词汇表中是一个单独的标记。然而，在“卷积神经网络”出现之前，我们将忽略序列信息，通过迭代字符串输入中的每个字符来创建输入的收缩one-hot向量表示。我们为以前未遇到的字符指定一个特殊的令牌，即UNK。由于我们仅从训练数据实例化词汇表，而且验证或测试数据中可能有惟一的字符，所以在字符词汇表中仍然使用UNK符号。

虽然我们在这个示例中使用了收缩的one-hot，但是在后面的实验中，将了解其他向量化方法，它们是one-hot编码的替代方法，有时甚至更好。具体来说，在该实验中，将看到一个热门矩阵，其中每个字符都是矩阵中的一个位置，并具有自己的热门向量。

# SurnameVectorizer 类
class SurnameVectorizer(object):
    def __init__(self, surname_vocab, nationality_vocab):
        """
        初始化 SurnameVectorizer。

        参数:
            surname_vocab (Vocabulary): 姓氏词汇表。
            nationality_vocab (Vocabulary): 国籍词汇表。
        """
        self.surname_vocab = surname_vocab
        self.nationality_vocab = nationality_vocab

    def vectorize(self, surname):
        """
        将姓氏向量化为一个一热编码向量。

        参数:
            surname (str): 要向量化的姓氏。

        返回:
            np.ndarray: 一热编码向量。
        """
        one_hot = np.zeros(len(self.surname_vocab), dtype=np.float32)  # 创建全零数组
        for token in surname:
            one_hot[self.surname_vocab.lookup_token(token)] = 1  # 将对应位置设为1
        return one_hot

    @classmethod
    def from_dataframe(cls, surname_df):
        """
        从数据框创建 SurnameVectorizer。

        参数:
            surname_df (pd.DataFrame): 包含姓氏和国籍的数据框。

        返回:
            SurnameVectorizer: SurnameVectorizer 类的一个实例。
        """
        surname_vocab = Vocabulary(unk_token="@")  # 创建姓氏词汇表
        nationality_vocab = Vocabulary(add_unk=False)  # 创建国籍词汇表

        for index, row in surname_df.iterrows():
            for letter in row.surname:
                surname_vocab.add_token(letter)  # 向姓氏词汇表中添加字母
            nationality_vocab.add_token(row.nationality)  # 向国籍词汇表中添加国籍

        return cls(surname_vocab, nationality_vocab)  # 返回 SurnameVectorizer 实例

4.2 构建与训练多层感知器模型

SurnameClassifier 是本实验前面介绍的MLP的实现。第一个线性层将输入向量映射到中间向量，并对该向量应用非线性。第二线性层将中间向量映射到预测向量。

在最后一步中，可选地应用softmax操作，以确保输出和为1;这就是所谓的“概率”。它是可选的原因与我们使用的损失函数的数学公式有关——交叉熵损失。我们研究了“损失函数”中的交叉熵损失。回想一下，交叉熵损失对于多类分类是最理想的，但是在训练过程中软最大值的计算不仅浪费而且在很多情况下并不稳定。

# SurnameClassifier 类
class SurnameClassifier(nn.Module):
    """ 用于姓氏分类的两层多层感知器 """
    def __init__(self, input_dim, hidden_dim, output_dim):
        """
        初始化分类器

        参数:
            input_dim (int): 输入向量的大小
            hidden_dim (int): 第一个线性层的输出大小
            output_dim (int): 第二个线性层的输出大小
        """
        super(SurnameClassifier, self).__init__()
        self.fc1 = nn.Linear(input_dim, hidden_dim)  # 第一个全连接层
        self.fc2 = nn.Linear(hidden_dim, output_dim)  # 第二个全连接层

    def forward(self, x_in, apply_softmax=False):
        """
        分类器的前向传播

        参数:
            x_in (torch.Tensor): 输入数据张量。
                x_in 的形状应该是 (batch, input_dim)
            apply_softmax (bool): 是否应用 softmax 激活函数的标志
                如果与交叉熵损失一起使用，则应为 False
        返回:
            torch.Tensor: 输出张量。其形状应该是 (batch, output_dim)
        """
        intermediate_vector = F.relu(self.fc1(x_in))  # 应用 ReLU 激活函数到第一个全连接层的输出
        prediction_vector = self.fc2(intermediate_vector)  # 第二个全连接层的输出

        if apply_softmax:
            prediction_vector = F.softmax(prediction_vector, dim=1)  # 如果标志为 True，则应用 softmax 激活函数

        return prediction_vector

4.3 使用多层感知器进行姓氏分类

我们使用一个Namespace对象来存储所有的超参数和路径信息。

args = Namespace(
    # 数据和路径信息
    surname_csv="surnames.csv",  # 存储姓氏数据的CSV文件路径
    vectorizer_file="vectorizer.json",  # 保存向量化器的JSON文件路径
    model_state_file="model.pth",  # 保存模型状态的文件路径
    save_dir="model_storage/ch4/surname_mlp",  # 保存模型的目录路径
    
    # 模型超参数
    hidden_dim=300,  # 隐藏层的维度
    
    # 训练超参数
    seed=1337,  # 随机种子，用于确保结果的可重复性
    num_epochs=100,  # 训练的总轮数
    early_stopping_criteria=5,  # 提前停止的标准
    learning_rate=0.001,  # 学习率
    batch_size=64,  # 批处理大小
    device='cpu'
    # 运行时选项省略以节省空间
)

接着就是数据加载和向量化，初始化模型

# 加载数据集并创建向量化器
dataset = SurnameDataset.load_dataset_and_make_vectorizer(args.surname_csv)
vectorizer = dataset.get_vectorizer()

# 创建 DataLoader
train_loader = DataLoader(dataset, batch_size=args.batch_size, shuffle=True)

# 初始化分类器
classifier = SurnameClassifier(input_dim=len(vectorizer.surname_vocab),
                               hidden_dim=args.hidden_dim,
                               output_dim=len(vectorizer.nationality_vocab))

# 将分类器移到指定设备
classifier = classifier.to(args.device)

# 定义损失函数
loss_func = nn.CrossEntropyLoss(dataset.class_weights)

# 定义优化器
optimizer = torch.optim.Adam(classifier.parameters(), lr=args.learning_rate)

以及模型训练

# 设定一些初始参数
num_epochs = args.num_epochs
device = args.device

# 设置模型为训练模式
classifier.train()

# 开始训练循环
for epoch in range(num_epochs):
    running_loss = 0.0

    for batch_index, batch_dict in enumerate(train_loader):
        # 将数据移动到指定设备
        batch_dict = {k: v.to(device) for k, v in batch_dict.items()}

        # --------------------------------------
        # step 1. zero the gradients
        optimizer.zero_grad()

        # step 2. compute the output
        y_pred = classifier(batch_dict['x_surname'])

        # step 3. compute the loss
        loss = loss_func(y_pred, batch_dict['y_nationality'])
        loss_batch = loss.to("cpu").item()
        running_loss += (loss_batch - running_loss) / (batch_index + 1)

        # step 4. use loss to produce gradients
        loss.backward()

        # step 5. use optimizer to take gradient step
        optimizer.step()

    print(f"Epoch {epoch+1}/{num_epochs}, Loss: {running_loss:.4f}")

在完成模型训练后，我们可以使用训练好的模型对新的姓氏进行国籍预测。以下是一个函数 predict_nationality，该函数接受一个姓氏，并返回模型预测的国籍及其概率。

def predict_nationality(name, classifier, vectorizer):
    """
    预测姓氏的国籍

    参数:
        name (str): 姓氏
        classifier (nn.Module): 已训练的分类器模型
        vectorizer (SurnameVectorizer): 向量化器对象

    返回:
        dict: 包含预测的国籍和概率的字典
    """
    # 将姓氏向量化
    vectorized_name = vectorizer.vectorize(name)
    vectorized_name = torch.tensor(vectorized_name).view(1, -1).float()  # 确保转换为浮点型张量

    # 将数据移到模型所在的设备
    vectorized_name = vectorized_name.to(next(classifier.parameters()).device)

    # 计算模型的输出
    result = classifier(vectorized_name, apply_softmax=True)

    # 获取最大概率和对应的索引
    probability_values, indices = result.max(dim=1)
    index = indices.item()

    # 检查索引是否在词汇表范围内
    if index >= len(vectorizer.nationality_vocab):
        raise ValueError(f"Index {index} is out of bounds for the nationality vocabulary.")

    # 查找对应的国籍
    predicted_nationality = vectorizer.nationality_vocab.lookup_token(index)
    probability_value = probability_values.item()

    return {'nationality': predicted_nationality,
            'probability': probability_value}

为了进一步分析和理解模型的预测结果，我们可以扩展预测函数，使其返回前k个最可能的国籍及其对应的概率。以下是一个函数 predict_topk_nationality，该函数接受一个姓氏和一个整数k，返回模型预测的前k个最可能的国籍及其概率。

def predict_topk_nationality(name, classifier, vectorizer, k=5):
    """
    预测姓氏的前k个最可能的国籍

    参数:
        name (str): 姓氏
        classifier (nn.Module): 已训练的分类器模型
        vectorizer (SurnameVectorizer): 向量化器对象
        k (int): 返回的前k个预测结果

    返回:
        list: 包含前k个预测国籍和概率的字典列表
    """
    # 将姓氏向量化
    vectorized_name = vectorizer.vectorize(name)
    vectorized_name = torch.tensor(vectorized_name).view(1, -1).float()  # 确保转换为浮点型张量

    # 将数据移到模型所在的设备
    vectorized_name = vectorized_name.to(next(classifier.parameters()).device)

    # 计算模型的输出
    prediction_vector = classifier(vectorized_name, apply_softmax=True)

    # 获取前k个最大概率和对应的索引
    probability_values, indices = torch.topk(prediction_vector, k=k, dim=1)

    # 转换为numpy数组并移除批处理维度
    probability_values = probability_values.detach().cpu().numpy()[0]
    indices = indices.detach().cpu().numpy()[0]

    results = []
    for prob_value, index in zip(probability_values, indices):
        nationality = vectorizer.nationality_vocab.lookup_token(index)
        results.append({'nationality': nationality,
                        'probability': prob_value})

    return results

5、实验结果

5.1 结果展示

上图展示了训练过程中每个周期（epoch）上的损失值（loss）变化情况。可以看到，随着训练周期的增加，损失值逐渐下降，表明模型在不断学习并优化其参数，从而提高其对训练数据的拟合能力。这样的损失值曲线常常用于评估模型训练的效果。

5.2 模型性能评估

这里用作者本人的姓氏去进行预测，可以看出，其预测效果其实并不好。其预测为中国人的置信度仅为0.13。

6、卷积神经网络的引入

6.1 CNN的基本概念

前面，我们深入研究了MLPs、由一系列线性层和非线性函数构建的神经网络。mlp不是利用顺序模式的最佳工具。例如，在姓氏数据集中，姓氏可以有(不同长度的)段，这些段可以显示出相当多关于其起源国家的信息(如“O’Neill”中的“O”、“Antonopoulos”中的“opoulos”、“Nagasawa”中的“sawa”或“Zhu”中的“Zh”)。这些段的长度可以是可变的，挑战是在不显式编码的情况下捕获它们。

在该部分中，我们将介绍卷积神经网络，这是一种非常适合检测空间子结构(并因此创建有意义的空间子结构)的神经网络。CNNs通过使用少量的权重来扫描输入数据张量来实现这一点。通过这种扫描，它们产生表示子结构检测(或不检测)的输出张量。

在本节的其余部分中，我们首先描述CNN的工作方式，以及在设计CNN时应该考虑的问题。我们深入研究CNN超参数，目的是提供直观的行为和这些超参数对输出的影响。最后，我们通过几个简单的例子逐步说明CNNs的机制。在“示例:使用CNN对姓氏进行分类”中，我们将深入研究一个更广泛的示例。

HISTORICAL CONTEXT

CNNs的名称和基本功能源于经典的数学运算卷积。卷积已经应用于各种工程学科，包括数字信号处理和计算机图形学。一般来说，卷积使用程序员指定的参数。这些参数被指定来匹配一些功能设计，如突出边缘或抑制高频声音。事实上，许多Photoshop滤镜都是应用于图像的固定卷积运算。然而，在深度学习和本实验中，我们从数据中学习卷积滤波器的参数，因此它对于解决当前的任务是最优的。

CNN Hyperparameters

为了理解不同的设计决策对CNN意味着什么，我们在图4-6中展示了一个示例。在本例中，单个“核”应用于输入矩阵。卷积运算(线性算子)的精确数学表达式对于理解这一节并不重要，但是从这个图中可以直观地看出，核是一个小的方阵，它被系统地应用于输入矩阵的不同位置。

输入矩阵与单个产生输出矩阵的卷积核（也称为特征映射）在输入矩阵的每个位置应用内核。在每个应用程序中，内核乘以输入矩阵的值及其自身的值，然后将这些乘法相加kernel具有以下超参数配置：kernel_size=2，stride=1，padding=0，以及dilation=1。这些超参数解释如下:

虽然经典卷积是通过指定核的具体值来设计的，但是CNN是通过指定控制CNN行为的超参数来设计的，然后使用梯度下降来为给定数据集找到最佳参数。两个主要的超参数控制卷积的形状(称为kernel_size)和卷积将在输入数据张量(称为stride)中相乘的位置。还有一些额外的超参数控制输入数据张量被0填充了多少(称为padding)，以及当应用到输入数据张量(称为dilation)时，乘法应该相隔多远。在下面的小节中，我们将更详细地介绍这些超参数。

DIMENSION OF THE CONVOLUTION OPERATION

首先要理解的概念是卷积运算的维数。在图4-6和本节的其他图中，我们使用二维卷积进行说明，但是根据数据的性质，还有更适合的其他维度的卷积。在PyTorch中，卷积可以是一维、二维或三维的，分别由Conv1d、Conv2d和Conv3d模块实现。一维卷积对于每个时间步都有一个特征向量的时间序列非常有用。在这种情况下，我们可以在序列维度上学习模式。NLP中的卷积运算大多是一维的卷积。另一方面，二维卷积试图捕捉数据中沿两个方向的时空模式;例如，在图像中沿高度和宽度维度——为什么二维卷积在图像处理中很流行。类似地，在三维卷积中，模式是沿着数据中的三维捕获的。例如，在视频数据中，信息是三维的，二维表示图像的帧，时间维表示帧的序列。就本课程而言，我们主要使用Conv1d。

CHANNELS

非正式地，通道(channel)是指沿输入中的每个点的特征维度。例如，在图像中，对应于RGB组件的图像中的每个像素有三个通道。在使用卷积时，文本数据也可以采用类似的概念。从概念上讲，如果文本文档中的“像素”是单词，那么通道的数量就是词汇表的大小。如果我们更细粒度地考虑字符的卷积，通道的数量就是字符集的大小(在本例中刚好是词汇表)。在PyTorch卷积实现中，输入通道的数量是in_channels参数。卷积操作可以在输出(out_channels)中产生多个通道。您可以将其视为卷积运算符将输入特征维“映射”到输出特征维。图 2 和图 3 说明了这个概念。

很难立即知道有多少输出通道适合当前的问题。为了简化这个困难，我们假设边界是1,1,024——我们可以有一个只有一个通道的卷积层，也可以有一个只有1,024个通道的卷积层。现在我们有了边界，接下来要考虑的是有多少个输入通道。一种常见的设计模式是，从一个卷积层到下一个卷积层，通道数量的缩减不超过2倍。这不是一个硬性的规则，但是它应该让您了解适当数量的out_channels是什么样子的。

KERNEL SIZE

核矩阵的宽度称为核大小(PyTorch中的kernel_size)。在图4-6中，核大小为2，而在图4-9中，我们显示了一个大小为3的内核。卷积将输入中的空间(或时间)本地信息组合在一起，每个卷积的本地信息量由内核大小控制。然而，通过增加核的大小，也会减少输出的大小(Dumoulin和Visin, 2016)。这就是为什么当核大小为3时，输出矩阵是图 4 中的2x2，而当核大小为2时，输出矩阵是图 1 中的3x3。

此外，可以将NLP应用程序中核大小的行为看作类似于通过查看单词组捕获语言模式的n-gram的行为。使用较小的核大小，可以捕获较小的频繁模式，而较大的核大小会导致较大的模式，这可能更有意义，但是发生的频率更低。较小的核大小会导致输出中的细粒度特性，而较大的核大小会导致粗粒度特性。

STRIDE

Stride控制卷积之间的步长。如果步长与核相同，则内核计算不会重叠。另一方面，如果跨度为1，则内核重叠最大。输出张量可以通过增加步幅的方式被有意的压缩来总结信息，如图 5 所示。

PADDING

即使stride和kernel_size允许控制每个计算出的特征值有多大范围，它们也有一个有害的、有时是无意的副作用，那就是缩小特征映射的总大小(卷积的输出)。为了抵消这一点，输入数据张量被人为地增加了长度(如果是一维、二维或三维)、高度(如果是二维或三维)和深度(如果是三维)，方法是在每个维度上附加和前置0。这意味着CNN将执行更多的卷积，但是输出形状可以控制，而不会影响所需的核大小、步幅或扩展。图6展示了正在运行的填充。

DILATION

膨胀控制卷积核如何应用于输入矩阵。在图4-12中，我们显示，将膨胀从1(默认值)增加到2意味着当应用于输入矩阵时，核的元素彼此之间是两个空格。另一种考虑这个问题的方法是在核中跨跃——在核中的元素或核的应用之间存在一个step size，即存在“holes”。这对于在不增加参数数量的情况下总结输入空间的更大区域是有用的。当卷积层被叠加时，扩张卷积被证明是非常有用的。连续扩张的卷积指数级地增大了“接受域”的大小；即网络在做出预测之前所看到的输入空间的大小。

6.2 CNN与MLP的对比

多层感知器

特点

全连接结构：MLP的每一层的神经元都与下一层的每一个神经元连接，这种全连接结构可以捕捉到数据的全局特征。
非线性映射：通过激活函数（如ReLU、Sigmoid），MLP可以对输入进行非线性变换，从而能够拟合复杂的函数关系。
易于实现：MLP结构相对简单，适合用于初学者的研究和教学。
局限性：由于全连接结构，MLP在处理高维输入（如图像、长文本序列）时，参数量巨大，容易导致过拟合，并且对局部特征的捕捉能力较差。

在文本处理中的应用

在处理文本数据时，MLP通常将文本表示为向量（如词袋模型、TF-IDF、词向量等），然后通过全连接层进行分类或回归任务。MLP不擅长捕捉文本中的局部模式，如n-gram特征。

卷积神经网络

特点

局部连接和权重共享：通过卷积操作，CNN能够高效地捕捉数据的局部模式（如文本中的n-gram特征）。
参数共享：卷积核在整个输入数据上共享同一组参数，减少了模型的参数数量，降低了过拟合风险。
平移不变性：卷积操作使得模型对输入的平移具有不变性，能够更好地处理变化的输入。
层次特征表示：通过多层卷积，CNN能够从低级特征（如边缘、纹理）逐渐提取高级特征（如形状、语义）。

在文本处理中的应用

在处理文本数据时，CNN通常将文本表示为矩阵（如字符或词的嵌入向量矩阵），通过一维卷积操作提取文本的局部特征（如n-gram），然后通过池化操作和全连接层进行分类或回归任务。CNN擅长捕捉文本中的局部模式，如短语、词组等特征。

比较与讨论

相同点

非线性变换：MLP和CNN都通过非线性激活函数进行非线性变换，从而能够拟合复杂的函数关系。
可微性：两者都是端到端的可微模型，可以通过反向传播算法进行训练。
应用领域：两者都广泛应用于文本分类、情感分析、命名实体识别等自然语言处理任务。

不同点

特征提取：MLP通过全连接层捕捉全局特征，而CNN通过卷积操作捕捉局部特征。CNN在处理具有局部依赖性的文本数据（如n-gram特征）时表现更好。
参数量：MLP的全连接结构导致参数量巨大，而CNN通过权重共享机制减少了参数量，降低了过拟合风险。
计算效率：由于参数共享，CNN的计算效率通常高于MLP，特别是在处理高维输入数据时。
平移不变性：CNN具有平移不变性，更适合处理位置变化的输入数据，而MLP缺乏这种特性。

6.3 使用CNN进行姓氏分类

为了证明CNN的有效性，让我们应用一个简单的CNN模型来分类姓氏。这项任务的许多细节与前面的MLP示例相同，但真正发生变化的是模型的构造和向量化过程。模型的输入，而不是我们在上一个例子中看到的收缩的onehot，将是一个onehot的矩阵。这种设计将使CNN能够更好地“view”字符的排列，并对在“示例:带有多层感知器的姓氏分类”中使用的收缩的onehot编码中丢失的序列信息进行编码。

虽然姓氏数据集之前在“示例:带有多层感知器的姓氏分类”中进行了描述，但建议参考“姓氏数据集”来了解它的描述。尽管我们使用了来自“示例:带有多层感知器的姓氏分类”中的相同数据集，但在实现上有一个不同之处:数据集由onehot向量矩阵组成，而不是一个收缩的onehot向量。为此，我们实现了一个数据集类，它跟踪最长的姓氏，并将其作为矩阵中包含的行数提供给矢量化器。列的数量是onehot向量的大小(词汇表的大小)。下面的代码显示了对SurnameDataset.__getitem__的更改。

class SurnameDataset(Dataset):
    def __init__(self, surname_df, vectorizer):
        """
        初始化 SurnameDataset

        参数:
            surname_df (pd.DataFrame): 包含姓氏数据的数据框。
            vectorizer (SurnameVectorizer): 一个 SurnameVectorizer 实例。
        """
        self.surname_df = surname_df
        self._vectorizer = vectorizer

        # 按照训练、验证和测试分割数据集
        self.train_df = self.surname_df[self.surname_df.split == 'train']
        self.train_size = len(self.train_df)

        self.val_df = self.surname_df[self.surname_df.split == 'val']
        self.validation_size = len(self.val_df)

        self.test_df = self.surname_df[self.surname_df.split == 'test']
        self.test_size = len(self.test_df)

        self._target_df = self.train_df  # 默认目标数据框为训练集

        # 计算类别权重以处理类别不平衡
        class_counts = self.surname_df['nationality'].value_counts().to_dict()
        sorted_counts = sorted(class_counts.items())
        self.class_weights = 1.0 / torch.tensor([count for _, count in sorted_counts], dtype=torch.float32)

    @classmethod
    def load_dataset_and_make_vectorizer(cls, surname_csv, max_seq_length):
        """
        从 CSV 文件加载数据集并创建向量化器。

        参数:
            surname_csv (str): 包含数据的 CSV 文件路径。
            max_seq_length (int): 序列的最大长度。

        返回:
            SurnameDataset: SurnameDataset 类的一个实例。
        """
        surname_df = pd.read_csv(surname_csv)
        # 随机分配 split 列
        np.random.seed(1337)
        mask = np.random.rand(len(surname_df))
        surname_df['split'] = np.where(mask <= 0.7, 'train',
                                       np.where(mask <= 0.85, 'val', 'test'))
        
        train_df = surname_df[surname_df.split == 'train']
        vectorizer = SurnameVectorizer.from_dataframe(train_df, max_seq_length)
        return cls(surname_df, vectorizer)

    def get_vectorizer(self):
        """
        获取向量化器。

        返回:
            SurnameVectorizer: 向量化器实例。
        """
        return self._vectorizer

    def set_split(self, split="train"):
        """
        设置目标数据框为指定的 split。

        参数:
            split (str): 可以是 'train', 'val' 或 'test'。
        """
        if split == "train":
            self._target_df = self.train_df
        elif split == "val":
            self._target_df = self.val_df
        elif split == "test":
            self._target_df = self.test_df
        else:
            raise ValueError("split 应该是 train, val 或 test 之一")

    def __len__(self):
        """
        返回当前目标数据框中的样本数量。

        返回:
            int: 样本数量。
        """
        return len(self._target_df)

    def __getitem__(self, index):
        """
        获取指定索引处的数据集样本。

        参数:
            index (int): 要检索的样本索引。

        返回:
            dict: 包含向量化的姓氏和国籍索引的字典。
        """
        row = self._target_df.iloc[index]

        surname_matrix = self._vectorizer.vectorize(row.surname, self._vectorizer.max_seq_length)
        nationality_index = self._vectorizer.nationality_vocab.lookup_token(row.nationality)

        return {'x_surname': surname_matrix,
                'y_nationality': nationality_index}

在向量化中，我们使用数据集中最长的姓氏来控制onehot矩阵的大小有两个原因。首先，将每一小批姓氏矩阵组合成一个三维张量，要求它们的大小相同。其次，使用数据集中最长的姓氏意味着可以以相同的方式处理每个小批处理。

class SurnameVectorizer(object):
    def __init__(self, surname_vocab, nationality_vocab, max_seq_length):
        """
        初始化 SurnameVectorizer

        参数:
            surname_vocab (Vocabulary): 姓氏词汇表。
            nationality_vocab (Vocabulary): 国籍词汇表。
            max_seq_length (int): 序列的最大长度。
        """
        self.surname_vocab = surname_vocab
        self.nationality_vocab = nationality_vocab
        self.max_seq_length = max_seq_length

    def vectorize(self, surname, max_seq_length=None):
        """
        将提供的姓氏向量化

        参数:
            surname (str): 姓氏
            max_seq_length (int, optional): 最大序列长度
        
        返回:
            np.ndarray: 一个填充或截断的姓氏矩阵
        """
        if max_seq_length is None:
            max_seq_length = self.max_seq_length
        
        # 创建一个全零数组，形状为 (词汇表长度, 最大序列长度)
        one_hot = np.zeros((len(self.surname_vocab), max_seq_length), dtype=np.float32)
        
        # 对姓氏中的每个字符进行向量化处理
        for i, token in enumerate(surname[:max_seq_length]):
            one_hot[self.surname_vocab.lookup_token(token), i] = 1
        
        return one_hot

    @classmethod
    def from_dataframe(cls, surname_df, max_seq_length):
        """
        从数据框创建 SurnameVectorizer

        参数:
            surname_df (pd.DataFrame): 包含姓氏和国籍的数据框。
            max_seq_length (int): 序列的最大长度。

        返回:
            SurnameVectorizer: SurnameVectorizer 类的一个实例。
        """
        surname_vocab = Vocabulary(unk_token="@")  # 创建姓氏词汇表
        nationality_vocab = Vocabulary(add_unk=False)  # 创建国籍词汇表

        for index, row in surname_df.iterrows():
            for letter in row.surname:
                surname_vocab.add_token(letter)  # 向姓氏词汇表中添加字母
            nationality_vocab.add_token(row.nationality)  # 向国籍词汇表中添加国籍

        return cls(surname_vocab, nationality_vocab, max_seq_length)  # 返回 SurnameVectorizer 实例

我们在该部分中创建的用于测试卷积层的“人工”数据与姓氏数据集中使用本例中的矢量化器的数据张量的大小完全匹配。具体来说，该模型类似于“卷积神经网络”，它使用一系列一维卷积来增量地计算更多的特征，从而得到一个单特征向量。

然而，本例中的新内容是使用sequence和ELU PyTorch模块。序列模块是封装线性操作序列的方便包装器。在这种情况下，我们使用它来封装Conv1d序列的应用程序。ELU是类似于实验3中介绍的ReLU的非线性函数，但是它不是将值裁剪到0以下，而是对它们求幂。

在本例中，我们将每个卷积的通道数与num_channels超参数绑定。我们可以选择不同数量的通道分别进行卷积运算。这样做需要优化更多的超参数。我们发现256足够大，可以使模型达到合理的性能。

class SurnameClassifier(nn.Module):
    def __init__(self, initial_num_channels, num_classes, num_channels):
        """
        初始化 SurnameClassifier

        参数:
            initial_num_channels (int): 输入特征向量的大小
            num_classes (int): 输出预测向量的大小
            num_channels (int): 在网络中使用的通道大小
        """
        super(SurnameClassifier, self).__init__()

        self.convnet = nn.Sequential(
            nn.Conv1d(in_channels=initial_num_channels,
                      out_channels=num_channels, kernel_size=3),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels,
                      kernel_size=3, stride=2),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels,
                      kernel_size=3, stride=2),
            nn.ELU(),
            nn.Conv1d(in_channels=num_channels, out_channels=num_channels,
                      kernel_size=3),
            nn.ELU()
        )
        self.fc = nn.Linear(num_channels, num_classes)

    def forward(self, x_surname, apply_softmax=False):
        """
        分类器的前向传播

        参数:
            x_surname (torch.Tensor): 输入数据张量。
                x_surname 的形状应该是 (batch, initial_num_channels, max_surname_length)
            apply_softmax (bool): 是否应用 softmax 激活函数的标志
                如果与交叉熵损失一起使用，则应为 False

        返回:
            torch.Tensor: 输出张量。其形状应该是 (batch, num_classes)
        """
        features = self.convnet(x_surname).squeeze(dim=2)  # 通过卷积网络并压缩维度
        prediction_vector = self.fc(features)  # 全连接层的输出

        if apply_softmax:
            prediction_vector = F.softmax(prediction_vector, dim=1)  # 如果标志为 True，则应用 softmax 激活函数

        return prediction_vector

其余部分与MLP部分的代码保持一致。

7、实验结果比较

7.1 MLP与CNN的分类结果对比

与前文对比可以看出，CNN的预测结果优于MLP

7.2 Dropout

什么是Dropout

Dropout是一种在神经网络训练过程中防止过拟合的技术。它的基本思想是在每次训练过程中，随机丢弃（即设置为零）一部分神经元的输出。这种方法迫使神经网络的每一层不依赖特定的神经元，而是更全面地利用网络中的所有神经元。

Dropout的实现

在每一层的训练过程中，对于每个神经元，以概率 $p$ 保留该神经元的输出，以概率 $1-p$ 将该神经元的输出置零。

在测试阶段，所有神经元都被激活，但为了保持输出的一致性，激活的神经元输出要乘以 $p$ 即：

$y=\frac{1}{p}\cdot y_{train}$

这种做法确保了训练和测试过程中网络的总输出水平保持一致。

Dropout对模型性能的影响

正面影响

提高泛化能力：通过防止过拟合，Dropout可以显著提高模型在未见数据上的表现。
训练更加稳定：由于减少了神经元的共适应性，网络在训练过程中不容易陷入局部最优。
更有效的特征学习：通过迫使网络使用所有特征，Dropout可以促进更有效的特征学习。

负面影响

训练时间增加：由于每次迭代需要对不同的神经元进行随机丢弃，训练时间会有所增加。
复杂性增加：在训练和测试过程中需要进行不同的处理，增加了实现的复杂性。
参数选择困难：Dropout的保留概率 $p$ 是一个超参数，需要通过实验进行选择，增加了调参的工作量。

8、实验中遇到的问题及解决方法

1. 数据预处理问题

问题

数据划分不均匀：训练集、验证集和测试集的划分可能导致类别分布不均匀，从而影响模型性能。

解决方法

数据划分：使用分层抽样方法，确保训练集、验证集和测试集中的类别分布相似，以提高模型的泛化能力。

2. 模型过拟合

问题

模型在训练集上表现良好，但在验证集和测试集上表现较差，说明模型可能过拟合训练数据。

解决方法

正则化：引入L2正则化（权重衰减）或L1正则化，防止模型参数过大。
Dropout：在模型中添加Dropout层，随机丢弃一部分神经元的输出，从而减少过拟合。
数据增强：增加训练数据的多样性，通过数据增强技术（如添加噪声、数据变换）来扩充训练数据。

3. 模型欠拟合

问题

模型在训练集和验证集上的表现都较差，说明模型可能欠拟合，无法捕捉数据的复杂特征。

解决方法

增加模型复杂度：增加模型的层数或每层的神经元数量，使模型能够学习更复杂的特征。
改进特征表示：使用更好的特征表示方法（如词嵌入）来提高输入数据的质量。
调整超参数：调整学习率、批处理大小等超参数，以提高模型的训练效果。

m0_67461772

关注

14
点赞
踩
31

收藏

觉得还不错? 一键收藏
0
评论
基于前馈神经网络的姓氏分类

在本实验中，使用了一个包含姓氏及其对应国籍的数据集。该数据集旨在通过姓氏来预测其所属的国籍。数据集包含多种国籍的姓氏，涉及的国家包括英语国家、阿拉伯国家、俄语国家、日语国家等。具体来说：姓氏数据集，它收集了来自18个不同国家的10,000个姓氏，这些姓氏是从互联网上不同的姓名来源收集的。该数据集具有一些使其有趣的属性。第一个性质是它是相当不平衡的。排名前三的课程占数据的60%以上:27%是英语，21%是俄语，14%是阿拉伯语。剩下的15个民族的频率也在下降——这也是语言特有的特性。
复制链接

扫一扫