任务目标: 通过对深圳10个区的二手房数据的清洗及处理,筛选对房价有显著影响的特征变量,对假设结论进行检验,确定特征变量,建立房价预测模型,并对假设情景进行模拟
目录
数据情况:
| 列名 | 列名含义 | 备注 | |||||
| district | 房屋所在区 | 深圳十个区:龙岗、龙华、宝安、南山、福田、罗湖、坪山、光明、盐田、大鹏新区 | |||||
| roomnum | 房间数 | 取值1~9 | |||||
| hall | 厅数 | 取值0~5 | |||||
| AREA | 面积 | 单位:㎡ | |||||
| C_floor | 楼层 | 分三档:middle、high、low | |||||
| school | 是否学区房 | 0(不是学区房),1(学区房) | |||||
| subway | 地铁 | 0(不靠近地铁),1(靠近地铁) | |||||
| per_price | 平米单价 | 单位:万元/㎡ |
一、数据清洗
爬取到的多个数据表格式整齐可直接合并
import os
import pandas as pd
pd.set_option('display.max_columns',None)
#待合并表格文件目录
data_path=r'H:\文件\深圳市二手房房价分析及预测\data'
#读取目录下所有文件
os.chdir(data_path)
loadfile=os.listdir()
df=pd.DataFrame()
#将多个xls文件合并
for i in loadfile:
locals()[i.split('.')[0]]=pd.read_excel(i)
df=pd.concat([df,locals()[i.split('.')[0]]])查看数据情况
print(df.shape)#(18514, 10)
#数据类型
print(df.dtypes)
#数据预览
print(df.head())
#是否有重复项
print(df.duplicated())
#查看缺失值情况
print(df.isna().sum()/df.shape[0]*100)
nul=[i[0] for i in df.isna().any().iteritems() if i[1]==True]
nul
#运行结果:
district 0.0
roomnum 0.0
hall 0.0
AREA 0.0
C_floor 0.0
school 0.0
subway 0.0
per_price 0.0
dtype: float64
#查看分类变量的取值
import sqlite3
con=sqlite3.connect(':memory:')
df.to_sql('df',con)
print(list(df))
for i in list (df[['district', 'roomnum', 'hall', 'C_floor', 'school', 'subway']]):
s=pd.read_sql_query('select distinct %s from df'%i,con)
print(s)
运行结果:
['district', 'roomnum', 'hall', 'AREA', 'C_floor', 'school', 'subway', 'per_price']
district
0 baoan
1 dapengxinqu
2 futian
3 guangming
4 longgang
5 longhua
6 luohu
7 nanshan
8 pingshan
9 yantian
roomnum
0 3
1 4
2 1
3 2
4 5
5 7
6 6
7 8
8 9
hall
0 2
1 1
2 0
3 3
4 4
5 5
6 6
C_floor
0 middle
1 high
2 low
school
0 0
1 1
subway
0 0
1 1
#将城区名称由拼音转汉字
dist_dict={'baoan': '宝安','dapengxinqu': '大鹏新区','futian': '福田','guangming': '光明','longgang': '龙岗','longhua': '龙华','luohu': '罗湖','nanshan': '南山','pingshan': '坪山','yantian':'盐田'}
df['district']=df['district'].apply(lambda x:dist_dict[x])
#查看描述基本信息(看是否存在异常值)
print(df.describe(include='all').T)
#删除后续分析不必要字段:
del df['Unnamed: 0']#Unnamed: 0作为源数据索引
del df['floor_num']
df.to_csv(r'G:\jupyter_project\secondhand_house\房屋信息表.csv',index=False,mode='w',encoding='gbk')查看结果:未发现数据异常
二、因变量分析
per_price:单位面积房价
tableau可视化

由上述可视化结果可知:样本数据中房屋单价主要集中在3-8万/㎡这一区间,其中5万/㎡占比最高
#最大值、最小值、均值、标准差、四分位数
print(df.per_price.agg(['max','min','mean','median','std']).T)
#运行结果:
# max 26.3968
# min 1.0101
# mean 6.118192
# median 5.246300
# std 3.050218
print(df.per_price.quantile([0.25,0.5,0.75]))
#运行结果:
# 0.25 4.0526
# 0.50 5.2463
# 0.75 7.3574三、自变量分析
3.1 分类变量分析
I:整体情况
#查看各分类变量值统计
for i in range(len(list(df))):
if i!=list(df).index('AREA') and i!=list(df).index('per_price'):
print(df.columns.values[i],':')
print(df[df.columns.values[i]].value_counts())
else:
continue
#运行结果:
district :
罗湖 3299
坪山 2574
南山 2403
光明 2073
龙华 1950
盐田 1492
龙岗 1472
福田 1264
宝安 1251
大鹏新区 736
Name: district, dtype: int64
roomnum :
3 8320
2 4524
4 3037
1 1624
5 780
6 139
8 45
7 41
9 4
Name: roomnum, dtype: int64
hall :
2 14667
1 3268
0 287
3 220
4 64
6 5
5 3
Name: hall, dtype: int64
C_floor :
middle 7512
high 5707
low 5295
Name: C_floor, dtype: int64
school :
1 10876
0 7638
Name: school, dtype: int64
subway :
1 9334
0 9180
Name: subway, dtype: int64II:各分量
- district 城区

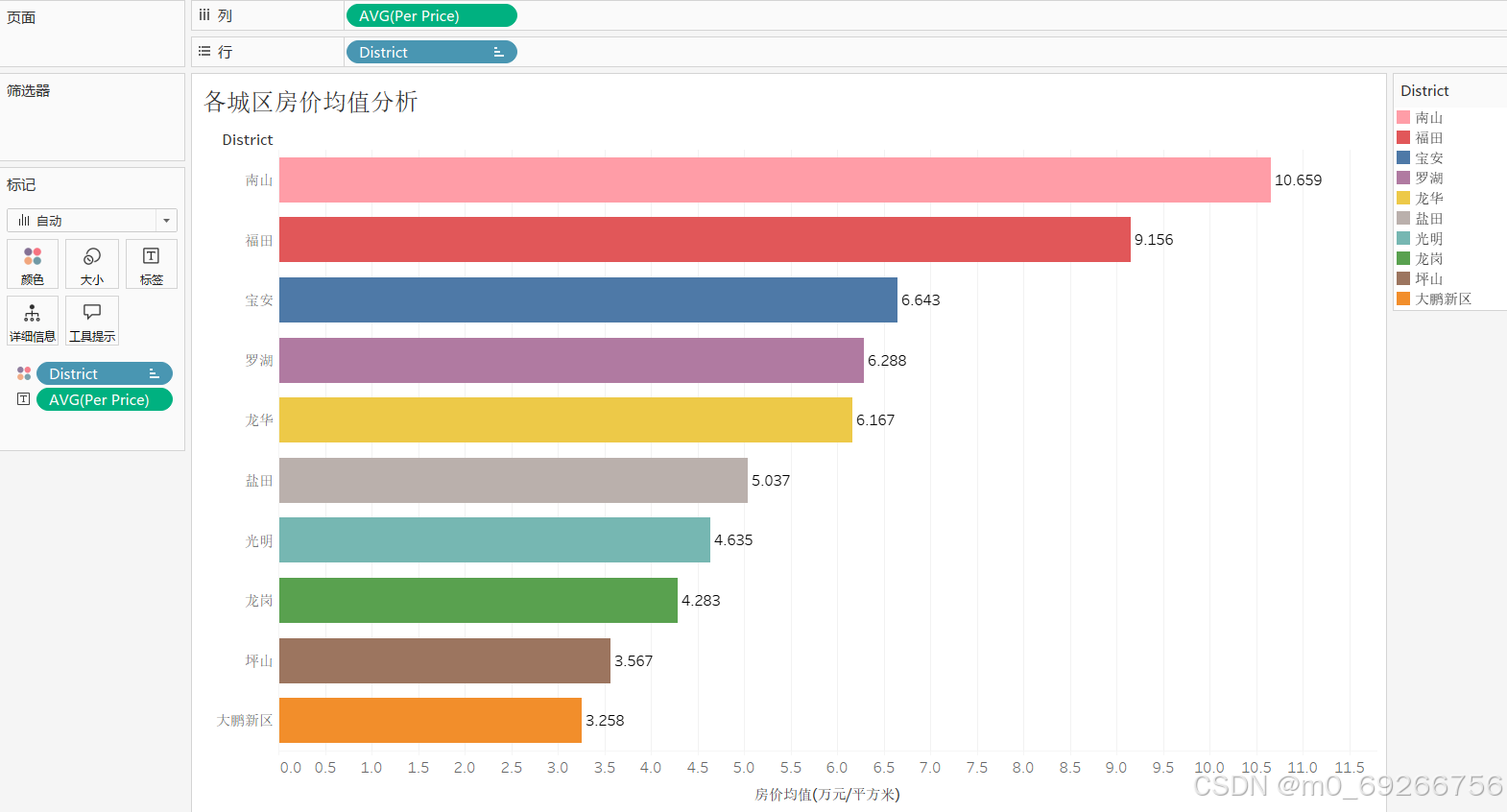

由上述可视化结果可知:各区数据样本量均在700以上,其中罗湖、坪山、南山占比较高占整体40%以上,其中南山、福田房屋单价均值较高均在9w/㎡以上,其中南山、福田、宝安值域分布最广,且城区对房屋单价有明显影响
- roomnum 房间数


由上述可视化结果可知:3个房间户型占比最高约占整体45%,6-9个房间户型占比最小,且房间数对房屋单价无明显影响
- hall 厅数


由上述可视化结果可知:2厅房间户型占比最高约占整体79%,4-6厅户型占比最小,且厅数对房屋单价浮动有明显影响
- C_floor 楼层

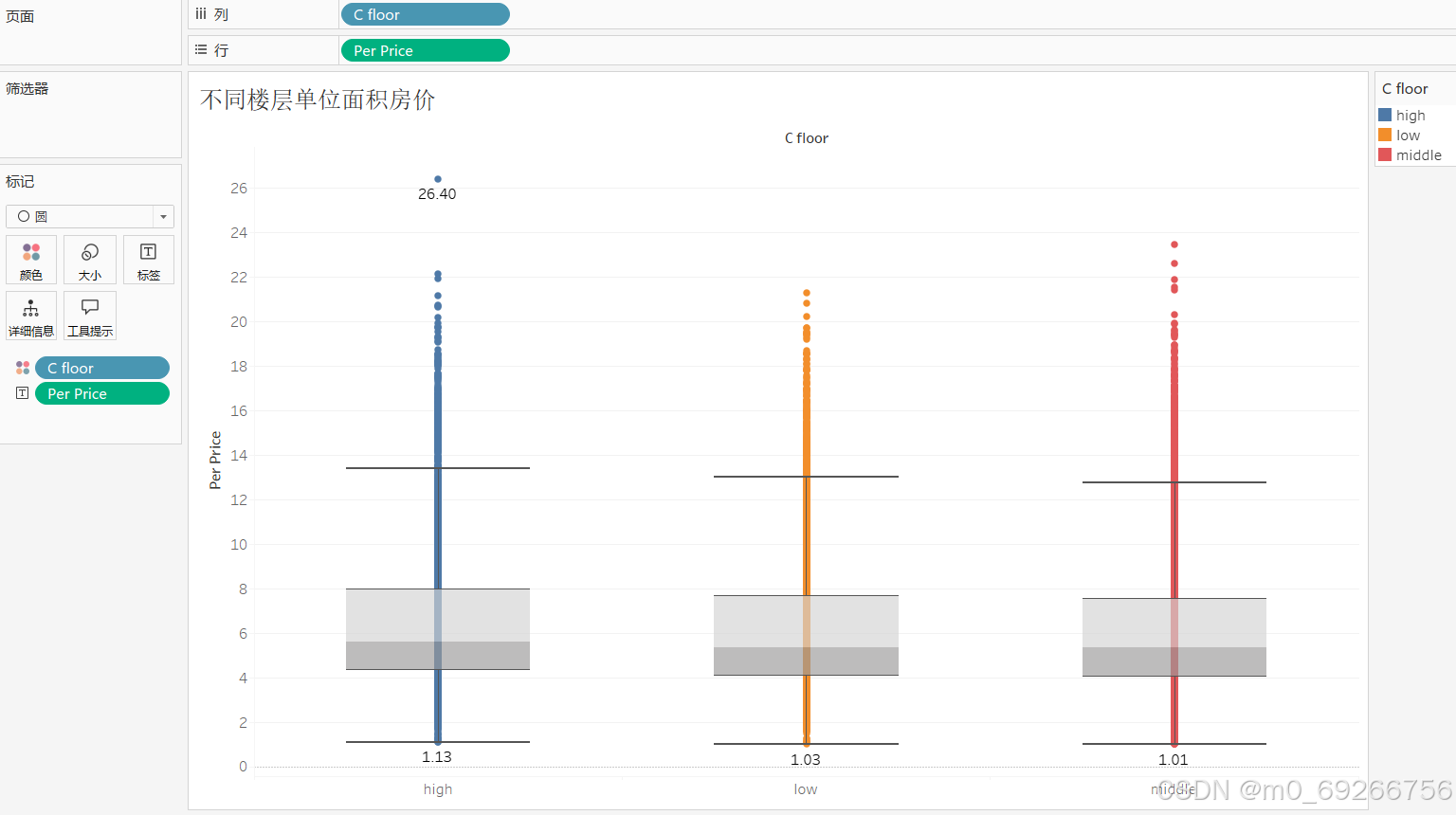
由上述可视化结果可知:middle楼层数据占比较高约40%,low、high楼层数据占比基本持平,各楼层房屋单价范围较为接近,且楼层对房屋单价无明显影响
- school 是否学区房

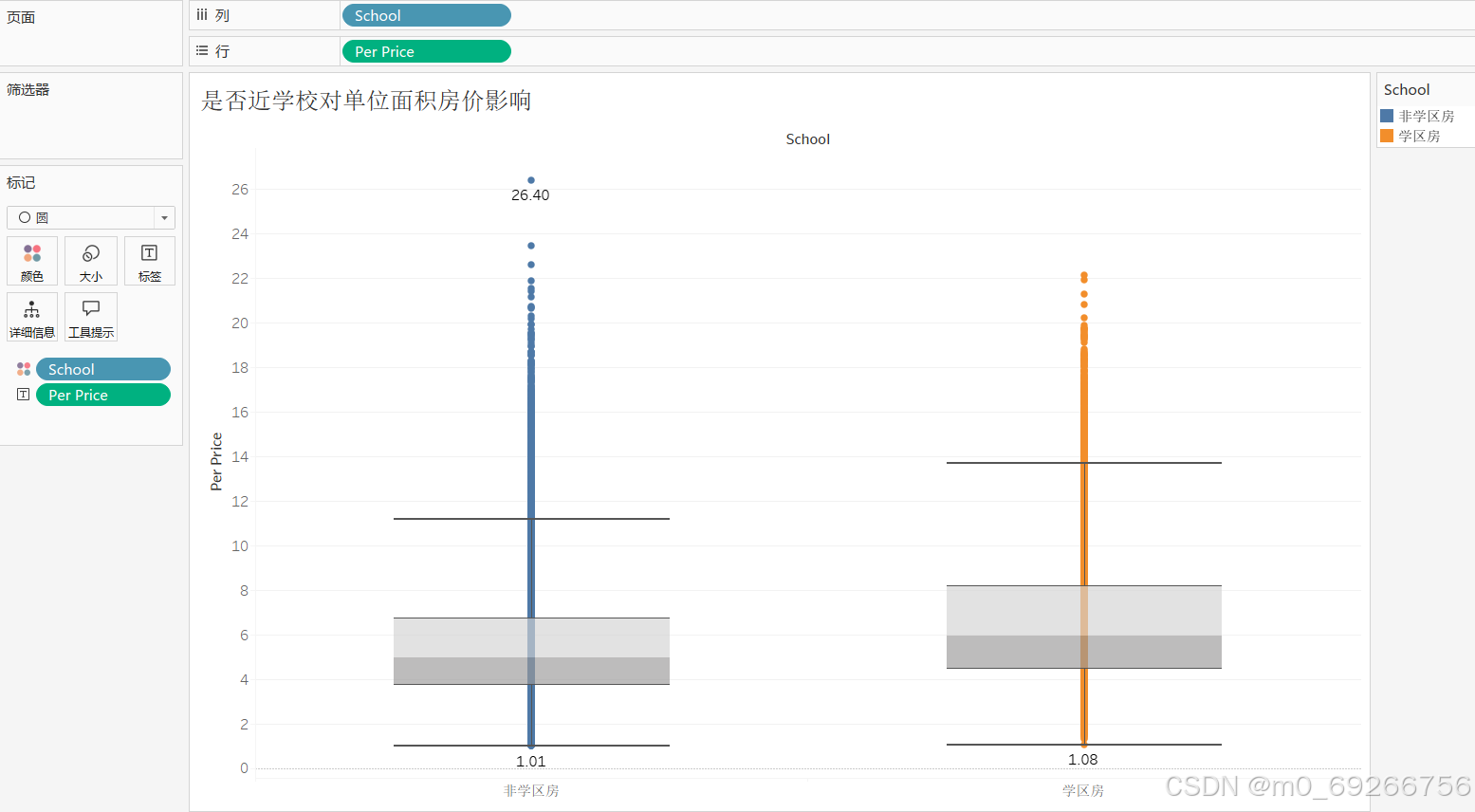
由上述可视化结果可知:学区房占比稍高,学区房房屋单价范围偏高
- subway 地铁

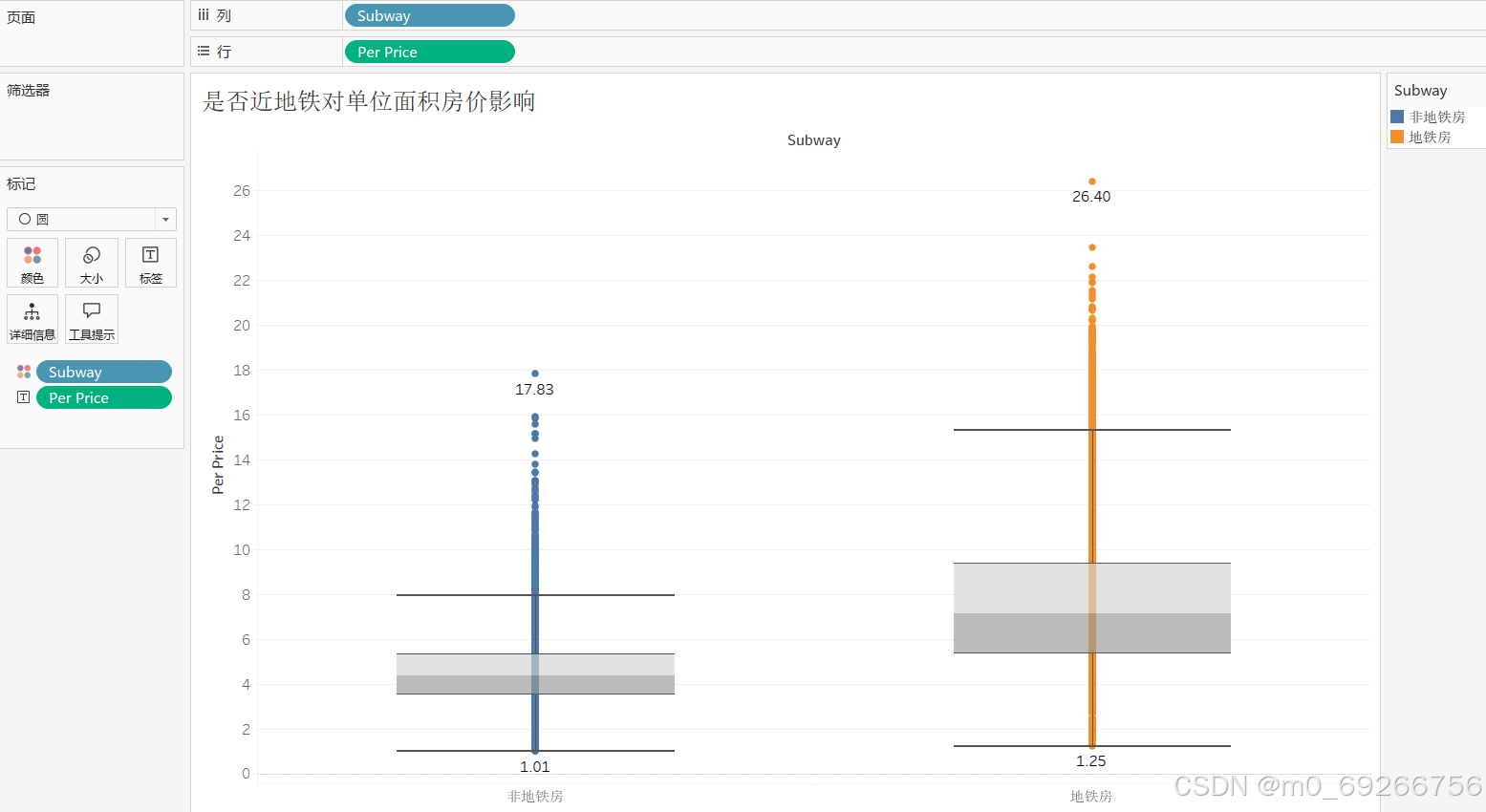

由上述可视化结果可知:地铁房和非地铁房占比持平,地铁房相比非地铁房房屋单价整体价格偏高、值域范围更广,地铁对房屋单价有明显影响,地铁房中学区房比非地铁房中学区房对房屋单价影响比重更大
3.2 连续变量分析
Area 房屋面积

由上述可视化结果可知:样本数据主要集中在50-120㎡这一区间,其中89㎡占比最高约占整体3.8%
#最大值、最小值、均值、标准差、四分位数
print(df.AREA.agg(['max','min','mean','median','std']).T)
#运行结果:
# max 697.200000
# min 15.000000
# mean 95.224924
# median 88.000000
# std 48.570130
print(df.AREA.quantile([0.25,0.5,0.75]))
#运行结果:
# 0.25 70.8000
# 0.50 88.0000
# 0.75 103.6875通过绘制散点图分析面积与房屋单价的关系,由上图可知房屋面积面积与房屋单价服从对数正态分布
四、建立房价预测对数线性模型
4.1 抽取特征
import pandas as pd
import numpy as np
data=pd.read_csv(r'房屋信息表.csv',sep=',',encoding='gbk')
#哑变量
#由之前的柱状图可知,厅数为3的要明显和其他数量的有较大的区别,对其进行转换
def hall(hall):
if hall== 3:
return 1
else:
return 0
data['Hall'] = data.apply(lambda x: hall(x.hall), axis=1)
def c_floor(C_floor):
if C_floor== "high":
return 2
if C_floor== "middle":
return 1
else:
return 0
data['C_Floor'] = data.apply(lambda x: c_floor(x.C_floor), axis=1)
a = pd.get_dummies(data['district'])
#上述分析可知面积和单位面积房价呈对数正态分布,所以对其求对数
data['AREA_log']=np.log(data['AREA'])
data['per_price_log']=np.log(data['per_price'])
#将所有变量合并
data=pd.concat([data,a],axis=1)
#删除多余变量
data=data.drop(['C_floor','district','hall','AREA','per_price'],axis=1)
print(data.columns)
# print(data.head())
# print(data.dtypes)
#运行结果:
Index(['roomnum', 'school', 'subway', 'Hall', 'C_Floor', 'AREA_log',
'per_price_log', '光明', '南山', '坪山', '大鹏新区', '宝安', '盐田', '福田', '罗湖','龙华','龙岗'],dtype='object')
'''
corr函数则是pandas库中用于计算DataFrame中各列之间相关系数的方法(对象必须是int类型)
相关系数是衡量两个变量之间线性关系强度和方向的统计量,其值介于-1和1之间
1:完全正相关
0:没有线性相关关系
-1:完全负相关
'''
for i in data.columns[:6]:
print(i,':',data[i].corr(data['per_price_log']))
#运行结果:
roomnum : 0.08594248891137699
school : 0.1894708119199801
subway : 0.5714992898809711
Hall : 0.09478192954282542
C_Floor : 0.03956623526535288
AREA_log : 0.18715179377926755
#删除相关性弱的特征
data=data.drop(['C_Floor','roomnum'],axis=1)4.2 抽样
y = data.loc[:, 'per_price_log']
x=data.drop(['per_price_log'],axis=1)
print(x.columns)
Index(['school', 'subway', 'Hall', 'AREA_log', '光明', '南山', '坪山', '大鹏新区', '宝安',
'盐田', '福田', '罗湖', '龙华', '龙岗'],
dtype='object')
# 数据分割,随机采样20%作为测试样本,其余作为训练样本
from sklearn.model_selection import train_test_split
'''
X_train 划分的训练集数据
X_test 划分的测试集数据
y_train 划分的训练集标签
y_test 划分的测试集标签
train_data 还未划分的数据集
train_target 还未划分的标签
random_state 随机数种子,应用于分割前对数据的洗牌。可以是int,RandomState实例或None,默认值=None。设成定值意味着,对于同一个数据集,只有第 一次运行是随机的,随后多次分割只要rondom_state相同,则划分结果也相同。
test_size 分割比例,默认为0.25,即测试集占完整数据集的比例
shuffle 是否在分割前对完整数据进行洗牌(打乱),默认为True:打乱
'''
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=1,stratify=a, test_size=0.2)
4.3训练模型
import statsmodels.api as sm
import matplotlib.pyplot as plt
#在反应变量和回归变量上使用 OLS()回归函数
Model=sm.OLS(y_train,x_train)
#获得拟合结果
Model=Model.fit()Model.summary
print(Model.summary())
#运行结果:
OLS Regression Results
==============================================================================
Dep. Variable: per_price_log R-squared: 0.633
Model: OLS Adj. R-squared: 0.633
Method: Least Squares F-statistic: 1964.
Date: Thu, 13 Feb 2025 Prob (F-statistic): 0.00
Time: 17:57:38 Log-Likelihood: -1687.3
No. Observations: 14811 AIC: 3403.
Df Residuals: 14797 BIC: 3509.
Df Model: 13
Covariance Type: nonrobust
==============================================================================
coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
school 0.0543 0.005 11.408 0.000 0.045 0.064
subway 0.1767 0.008 22.720 0.000 0.161 0.192
Hall 0.2362 0.021 11.268 0.000 0.195 0.277
AREA_log 0.1586 0.006 27.999 0.000 0.147 0.170
光明 0.7820 0.026 30.022 0.000 0.731 0.833
南山 1.3663 0.028 48.069 0.000 1.311 1.422
坪山 0.5134 0.026 19.664 0.000 0.462 0.565
大鹏新区 0.4083 0.028 14.454 0.000 0.353 0.464
宝安 1.0052 0.027 36.868 0.000 0.952 1.059
盐田 0.7990 0.028 28.779 0.000 0.745 0.853
福田 1.2286 0.029 43.084 0.000 1.173 1.284
罗湖 0.9348 0.026 36.482 0.000 0.885 0.985
龙华 0.9231 0.027 34.192 0.000 0.870 0.976
龙岗 0.5748 0.027 21.263 0.000 0.522 0.628
==============================================================================
Omnibus: 2453.093 Durbin-Watson: 1.965
Prob(Omnibus): 0.000 Jarque-Bera (JB): 13778.176
Skew: -0.680 Prob(JB): 0.00
Kurtosis: 7.525 Cond. No. 169.
==============================================================================
#画模型
x = Model.predict(x_test)
plt.figure(figsize=(8,8)) #设置画布
plt.scatter(x,y_test,color='black')
plt.xlabel('predict1',fontname='SimHei',size=15)
plt.ylabel('resid1',fontname='SimHei',size=15)
plt.show()
4.4 模型预测
# 导出模型文件
import joblib
joblib.dump(Model,'Model.pickle')
#预测结果
import math
pX=pd.DataFrame({'school':[1],'subway':[1],'Hall':[0],'AREA_log':[np.log(80)],'光明':[0],'南山':[1],'坪山':[0],'大鹏新区':[0],'宝安':[0],'盐田':[0],'福田':[0],'罗湖':[0],'龙华':[0],'龙岗':[0]})
#Model.predict(sm.add_constant(pX,has_constant='add'))
x=Model.predict(pX)
print("单位面积房价: ",round(math.exp(x),2), "万元/平方米")
print("总价:",round(math.exp(x)*80,2), "万元")#预测结果:
单位面积房价: 9.9 万元/平方米
总价: 791.8 万元


























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








