判别分析例题

例一

---

解：
（1）距离判别准则，使用马氏距离来判断，样品到第i个总体的马氏距离为

$d_i^2(x)=$ $\frac{(x-{\mu }_i{)}^2}{{\sigma }_i^2}$

分别计算出样品x=2.5到三个总体的距离为：

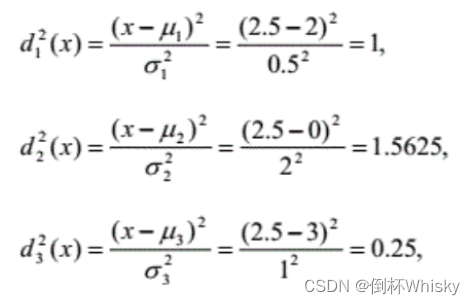
应选择距离最小的，即$d_3^2(x)$，所以按照距离判别准则应把样品归为$G_3$

（2）
样品属于总体i的后验概率为：

$z_i$(x)=ln $q_i$- $\frac{1}{2}$ln| ${\Sigma }_i$|- $\frac{1}{2}$ $d_i^2(x)$

由于题目已知先验概率$q_i$相等，可以只计算-ln|${\Sigma }_i$|-$d_i^2(x)$的部分，去掉负号计算如下

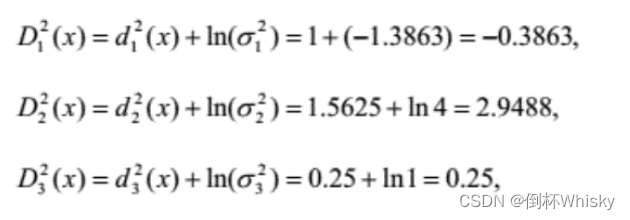
选择最小的，因此样品判归为$G_1$
（如果不去掉负号，直接计算后验概率，应选择最大的，表示样品属于该类的概率最大）

---

例二

---

解：
这题和上一题一样，只不过正态总体从一维变成了二维的。
（1）样本t到总体i的马氏距离：

$d_i^2(x_{(t)}，G_i)=$ ( $x_{(t)}$- ${\mu }_i$)’ ${\Sigma }_i^{-1}$( $x_{(t)}$- ${\mu }_i$)

对于样品$x_{(1)}$：

$d_1^2(x_{(1)}，G_1)=$ 25
$d_2^2(x_{(1)}，G_2)=$ 21.25

所以应判归$G_2$

对于样品$x_{(2)}$：

$d_1^2(x_{(2)}，G_1)=$ 50
$d_2^2(x_{(2)}，G_2)=$ 12.5

所以应判归$G_2$。

（2）样品属于总体i的后验概率为：

$z_i$(x)=ln $q_i$- $\frac{1}{2}$ln| ${\Sigma }_i$|- $\frac{1}{2}$ $d_i^2(x)$

此题也是先验概率相同，因此也可以只计算后面两项，取最小值
（如果先验概率和协方差阵都相同，那么就等价于距离判别法）
我在这里选择把后验概率计算出来，取最大值：
对于样本$x_{(1)}$：

$z_1$(x)=ln$\frac{1}{2}$-$\frac{1}{2}$ln|${\Sigma }_1$|-$\frac{1}{2}$$d_1^2(x_{(1)}，G_1)$=-1-12.5=-13.5
$z_2$(x)=ln$\frac{1}{2}$-$\frac{1}{2}$ln|${\Sigma }_2$|-$\frac{1}{2}$$d_2^2(x_{(1)}，G_2)$=-1-2-10.625=-13.625

应该选大的那个，所以应判归$G_1$

对于样本$x_{(2)}$：

$z_1$(x)=ln$\frac{1}{2}$-$\frac{1}{2}$ln|${\Sigma }_1$|-$\frac{1}{2}$$d_1^2(x_{(2)}，G_1)$=-1-25=-26
$z_2$(x)=ln$\frac{1}{2}$-$\frac{1}{2}$ln|${\Sigma }_2$|-$\frac{1}{2}$$d_2^2(x_{(2)}，G_2)$=-1-2-6.25=-9.25

应判归$G_2$