【python算法系列十二】平衡二叉树（AVL树）

 平衡二叉树是一种特别形式的二叉搜索树，它采用平衡化旋转来避免二叉搜索树出现退化的情况。

二叉搜索树的效率

理论上来说，对二叉搜索树进行一次操作的时间复杂度是 O(lgn)，这是因为二叉搜索树在理想状态下是近似于完全二叉树的。但是，在实际操作中，二叉搜索树很容易退化成线性的数据结构。例如，往二叉搜索树中插入一个有序序列，这时会得到一条链，如图 1 所示。

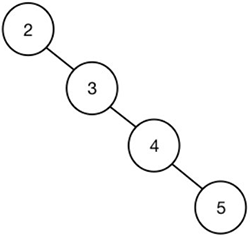
图 1：二叉搜索树退化成线性

这时候，对二叉搜索树进行操作的平均时间复杂度就会退化成 O(n)。左右子树的大小相差巨大的二叉搜索树，就处于非常不平衡的状态。这样的状态会使操作的时间复杂度大大提高。为了维持二叉搜索树的平衡状态，就出现了不同的平衡二叉树算法。

 AVL树

本节教程要讲到的平衡二叉树，又称为 AVL 树。它维持二叉搜索树平衡的根本在于持续维护这样一个性质：二叉搜索树中，每一个节点的左右子树深度差的绝对值不大于1。

举例来说，图 2（a）所示为 AVL 树，而图 2（b）所示则不是 AVL 树。

图 2：两棵二叉树

那么，如何判断一棵树是否符合 AVL 树的性质？答案就是维护每个节点的平衡因子。每个节点的平衡因子即为节点左子树的深度减去右子树的深度得到的差。在符合 AVL 性质的情况下，平衡因子只能取 -1、0、1。

正因为这样，在插入或删除一个节点之后，要从插入或删除的位置沿通向根的路径回溯，更新这些经过的节点的平衡因子。在检测到当前节点的平衡因子的绝对值大于1时，停止回溯，根据回溯路径中当前节点以及当前节点深度+1 和深度+2 两层节点的位置，选择旋转方法对二叉树的结构进行调整。

如果一棵平衡二叉树中的节点发生了变化，使二叉树不再平衡，此时需要采用平衡化旋转来调整树的结构，使得在不破坏二叉搜索树性质的情况下，让二叉树重新达到平衡。

平衡化旋转分为两种：单向旋转和双向旋转。如果回溯路径中当前节点以及下两层节点处于一条直线上，就可以采用单向旋转。如果在下两层的节点中，每一个节点都是父亲节点的右孩子，那么如图 3 所示，此时采用单向左旋。

图 3：单向左旋

 由于此处 A<B<C，所以左旋后并不破坏二叉搜索树的性质，而刚好使得平衡因子恢复到符合 AVL 树性质的大小。

这样的过程同样可以用图来展示。举例来说，在图 4 这样一棵平衡二叉树中插入节点后，整棵树就变得不平衡了。每个节点上方的数字就是该节点的平衡因子，而长方形代表子树，长方形里面的式子等于它的深度。

图 4：插入节点后平衡因子变化

 要想调整二叉树的结构，这里就要用到平衡左旋了。我们取每一棵子树的根节点来代表这一整棵子树，用一共 5 个节点来演示单向左旋的过程。图 5 所示就是单向左旋的效果。

图 5：单向左旋

 平衡树的结构最后被调整成了图 6 所示这样，而平衡因子也重新变得符合 AVL 树性质了。

图 6：调整完毕

 同样的道理，如果需要进行平衡旋转时，当前节点的下两层节点都是父节点的左孩子，那么就需要采用单向右旋。单向右旋的道理和单向左旋非常相似，下面就主要用图来演示，不多做讲解了。单向右旋的过程如图 7～图 9 所示。