题目介绍
链接: 611. 有效三角形的个数

思路分析
如果判断三个数能否构成一个三角形,相信大家都知道:
只要任意两边之和大于第三边即可。
比如三条边长度为a,b,c
那只要满足
a+b>c
a+c>b
b+c>a
但是,这样要判断三个条件,我们来介绍另一种方法:
如果三条边的长短已经知道:a<=b<=c
那么此时只需满足较短的两条边之和大于最长的那条边,即
a+b>c
那么它们就一定能构成一个三角形,另外两个条件就不需要判断了
原理很简单,因为c是最大的,c+一个数一定比另外两条边还大。
那题目呢,是给定一个包含非负整数的数组 nums ,要返回其中可以组成三角形三条边的三元组个数。
所以,判断的时候,我们可以先给数组排个序(升序)
然后呢,我们就可以用双指针来解决这道题,具体怎么做呢?我们来看一个例子:
给这样一个数组
最大值是10,所以我们先让固定c为10
那a,b呢?
一个指向剩余区间的最大值,一个指向最小值
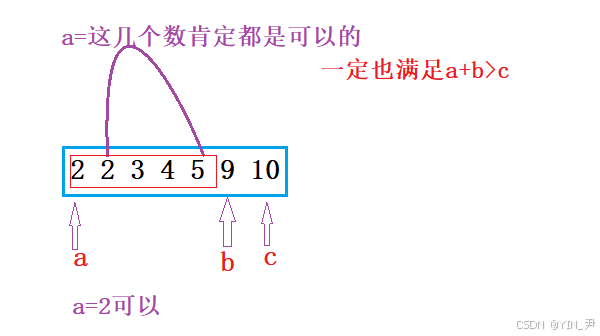
然后判断,此时的a+b=11,当然大于10(第一种情况:a+b>c),所以当前这一组是满足的,可以构成三角形。
然后我们观察,此时a是最小的,所以此时ab之间的数据都是>=a的,所以中间的这些数据和b相加一定都大于此时的c。
一共种呢,就是b的下标-c的下标
当前情况下就是5-0=5种。
所以中间的情况就不用判断了。b=9时一共5种情况可行。
假设两个指针left和right分别指向ab,那接下来只需让right--即可,判断c=10,b=5时候的情况
此时a+b<c(第二种情况:a+b<=c)
所以构不成三角形,并且,可以断定此时a和ab之间的数都相加都不大于c,因为这些数都比此时的b(5)小
所以固定c为10的情况下,a=2时,跟2 3 4 5都不行(9已经判断过了)
所以此时让left++,看后面的行不行(后面的数一定>=2,因为已经排序)
后序也是如此进行判断。
这一轮结束后(当left>=right结束),固定c为10的情况就计算完了,只需让c指向9,right从c的前面开始,left还从0下标开始,进重复上述操作,行下一轮的判断即可。
总结一下:
- 先固定c为最大的数
- 定义双指针,按照上述逻辑,判断出当前情况下符合条件的三元组个数。
如果a+b>c,b前面的元素个数就是b为当前值的情况下符合条件的三元组个数,然后b往前移(right- -);
如果a+b<=c,说明a为当前值的情况下找不到满足条件的,让a往后移(left++),再重新判断- 固定c为次大的数,重复上述操作,当c前面的数小于2个,就结束了(即c的下标<2)
AC代码


class Solution {
public:
int triangleNumber(vector<int>& nums) {
sort(nums.begin(),nums.end());
int index_c=nums.size()-1;//c的下标
int count=0;
while(index_c>=2)//index_c<2,此时左边的数就不够两个了
{
int left=0;//标识a的位置
int right=index_c-1;//b的位置
while(left<right)
{
if((nums[left]+nums[right])>nums[index_c])
{
count+=(right-left);
--right;
}
else
++left;
}
--index_c;
}
return count;
}
};































 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










