
例(1)这样想绝对值来算是错误的 *
定义里的绝对值代表的几何意义是距离,
|xn-a|<ε表示xn与a的距离小于ε
ε可以任意小,所以|xn-a|<ε表示xn与a无限接近,即n趋于无穷时xn的极限为a
如果不加绝对值,不能解释xn小于a的情况
还有就是,既不收敛也不发散的函数不存在,要么收敛要么发散。
(-1)的n次方/n还挺有意思的,发现了几道题都是关于这个函数

它的收敛如图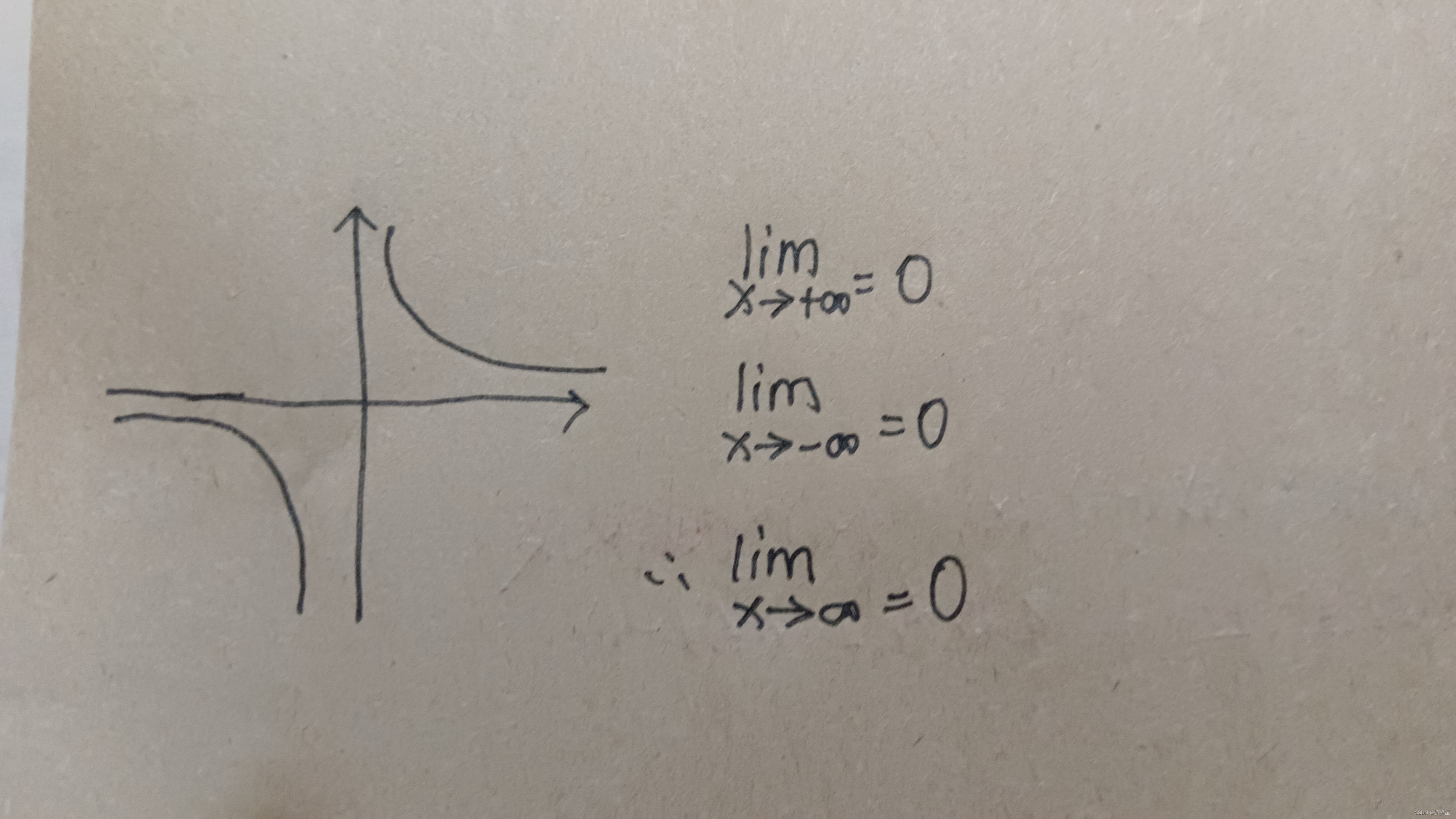

数列求极限可能会用的等差或者等比数列的求和公式,或者裂项公式


函数的极限





例(1)这样想绝对值来算是错误的 *
定义里的绝对值代表的几何意义是距离,
|xn-a|<ε表示xn与a的距离小于ε
ε可以任意小,所以|xn-a|<ε表示xn与a无限接近,即n趋于无穷时xn的极限为a
如果不加绝对值,不能解释xn小于a的情况
还有就是,既不收敛也不发散的函数不存在,要么收敛要么发散。
(-1)的n次方/n还挺有意思的,发现了几道题都是关于这个函数

它的收敛如图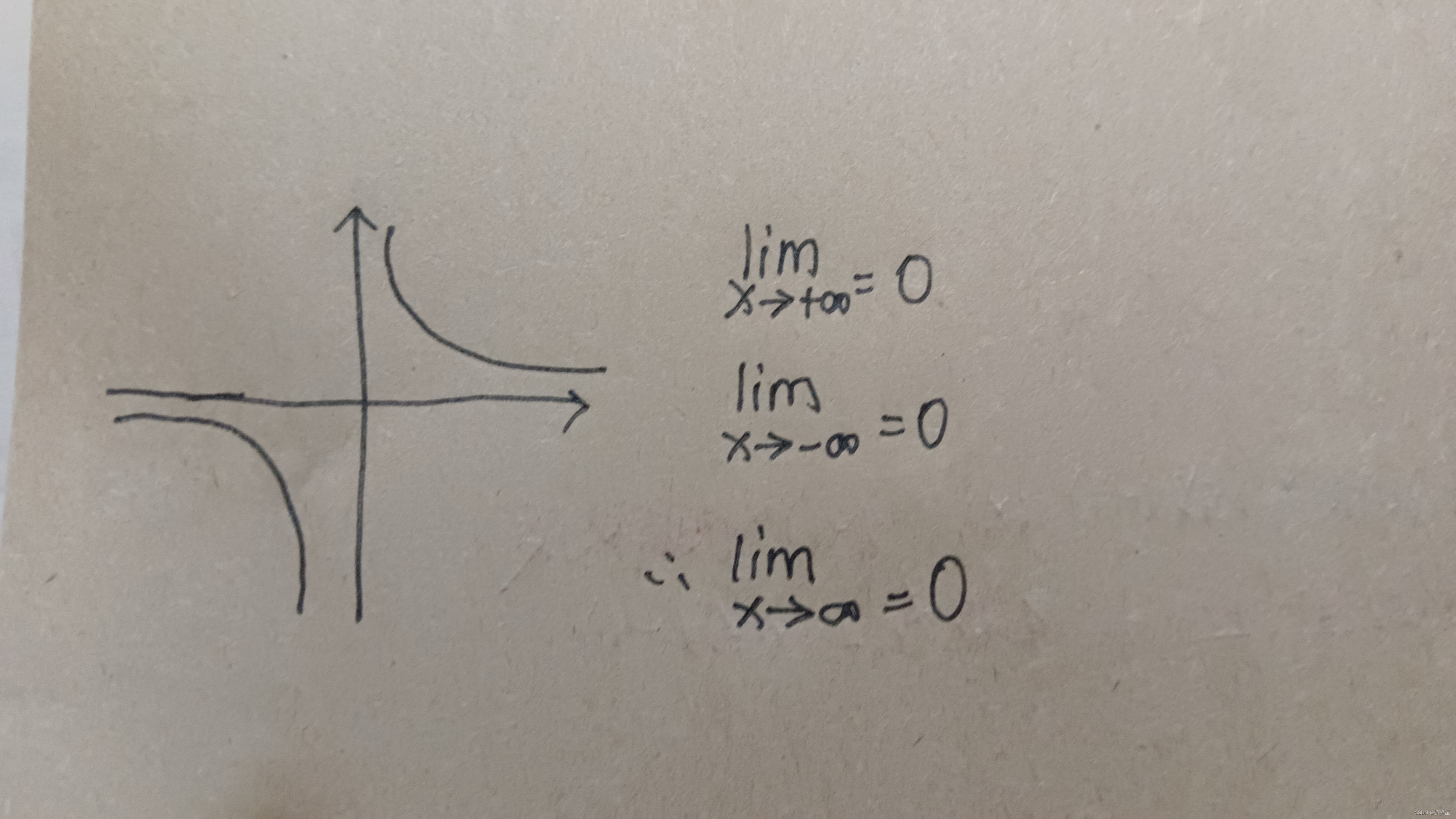

数列求极限可能会用的等差或者等比数列的求和公式,或者裂项公式


函数的极限





 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


