牛客周赛35

重新启动2.0

已于 2024-03-05 20:38:10 修改

阅读量962

点赞数 22

文章标签：算法

于 2024-03-05 17:45:37 首次发布

本文链接：https://blog.csdn.net/m0_73395592/article/details/136483177

版权

A

小红的字符串切割

题意：

签到题

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+20;
ll n;
int main()
{
    string s;
    cin >> s;
    for(int i = 0 ; i < s.size() ; i++) {
        if(i == s.size() / 2)
            cout<<"\n";
        cout << s[i];
        
    }
    return 0;
}

B

小红的数组分配

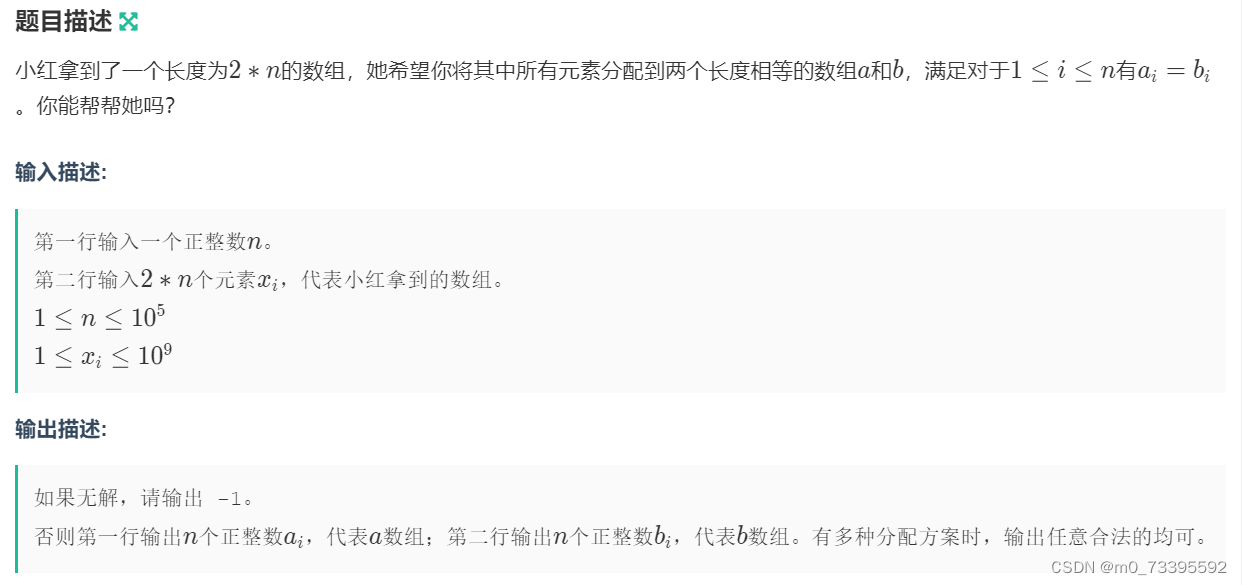
题意：

首先如果要实现原数组平分而且两个数组每个位置的值是相等的，必须满足所有原数组出现过的值必须是出现数量是偶数

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=2e5+20;
ll n;
int main()
{
    cin >> n;
    set<ll>ans;
    map<ll,ll>cnt;
    ll x;
    for(int i  = 1 ;i <= 2*n ; i++)
    {
        cin >> x;
        ans.insert(x);
        cnt[x]++;
        
    }
    vector<ll>res;
    for(auto it:ans)
    {
        if(cnt[it]%2!=0)
        {
            cout<<-1;
            return 0;
        }
        for(int i = 1 ; i <= cnt[it] / 2 ; i++)
            res.push_back(it);
    }
    for(int i = 0 ; i < res.size() ; i++)
    {
        cout<<res[i]<<" ";
    }
    cout<<"\n";
    for(int i = 0 ; i < res.size() ; i++)
    {
        cout<<res[i]<<" ";
    }
    return 0;
}

C

小红关鸡

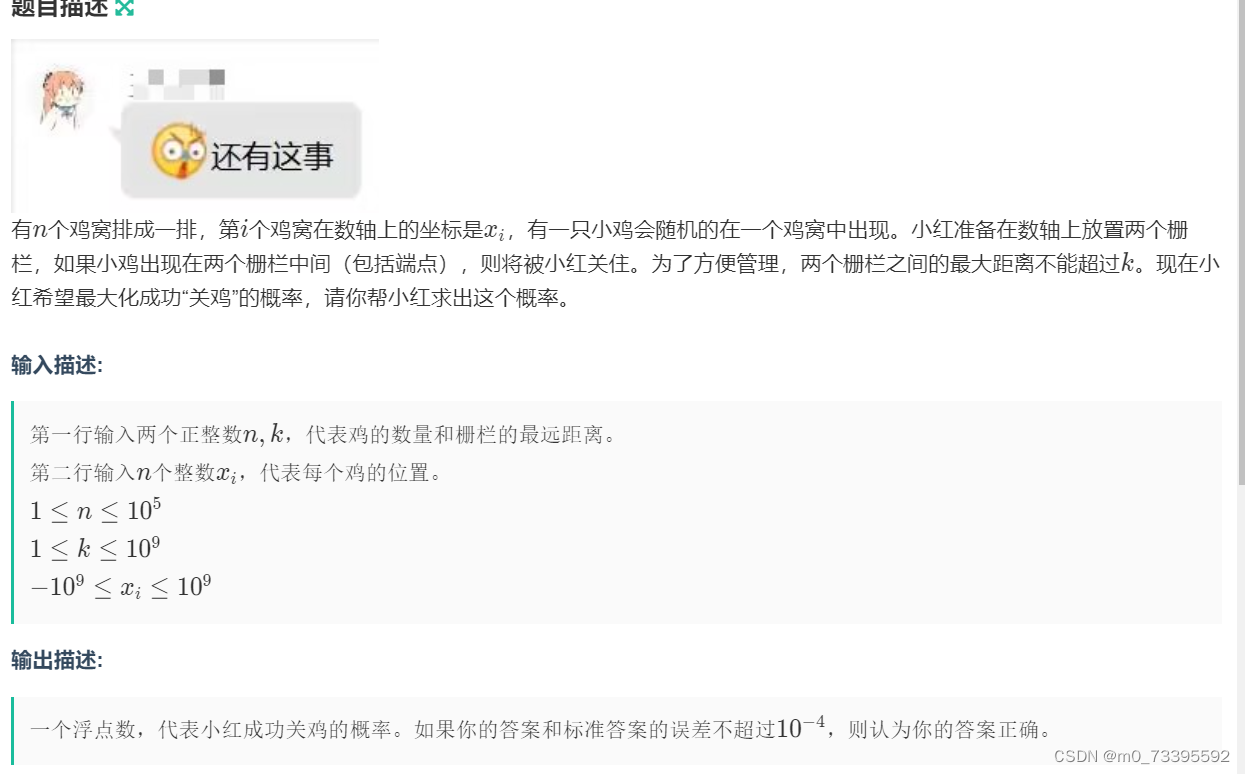
题意：

这题我先排了个序，我遍历了每个点，然后而二分查找第一个与改点距离大于等于k的点，然后定义一个ans保证是最大的数量

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+20;
ll a[N];
ll n,k;
int main()
{
    cin >> n >> k;
    for(int i = 1 ; i <= n ; i++)
    {
        cin >> a[i];
    }
    sort(a+1,a+1+n);
    ll ans = -1;
    for(ll i = 1 ; i<= n ; i++)
    {
        ll pos = upper_bound(a+1,a+1+n,a[i]+k)-a;
        if(a[pos] == a[i]+k)
        {
            ans = max(ans,pos-i+1);
        }
        else
        {
            ans = max(ans,pos-i);
        }
        if(a[i] + k >= a[n])
            break;
    }
    printf("%.4lf",1.0*ans/n);
    return 0;
}

D

小红的排列构造

题意：

通过观察可以发现，数组唯一有问题的值只有两种 1.已经出现过一次 2.大于n的数，我们只要把这些有问题的数的位置记录下来，没问题的数放到set里面，然后遍历set，缺哪个值我们就用之前记录的位置去补。

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
const int N=1e5+20;
ll a[N];
ll n,k;
int main()
{
    cin >> n;
    map<ll,ll>cnt;
    vector<ll>res;
    for(int i = 1; i <= n ; i++)
    {
        cin >> a[i];
        if(cnt[a[i]]>=1 || a[i] > n)
        {
            res.push_back(i);
        }
        cnt[a[i]]++;
    }
    vector<ll>ans;
    cout<<res.size()<<"\n";
    for(int i = 1 ; i <= n ; i++)
    {
        if(cnt[i]==0)
            ans.push_back(i);
    }
    for(int i = 0 ; i < res.size() ; i++)
    {
        cout<<res[i] <<" "<<ans[i]<<"\n";
    }
    return 0;
}

E

小红的无向图构造

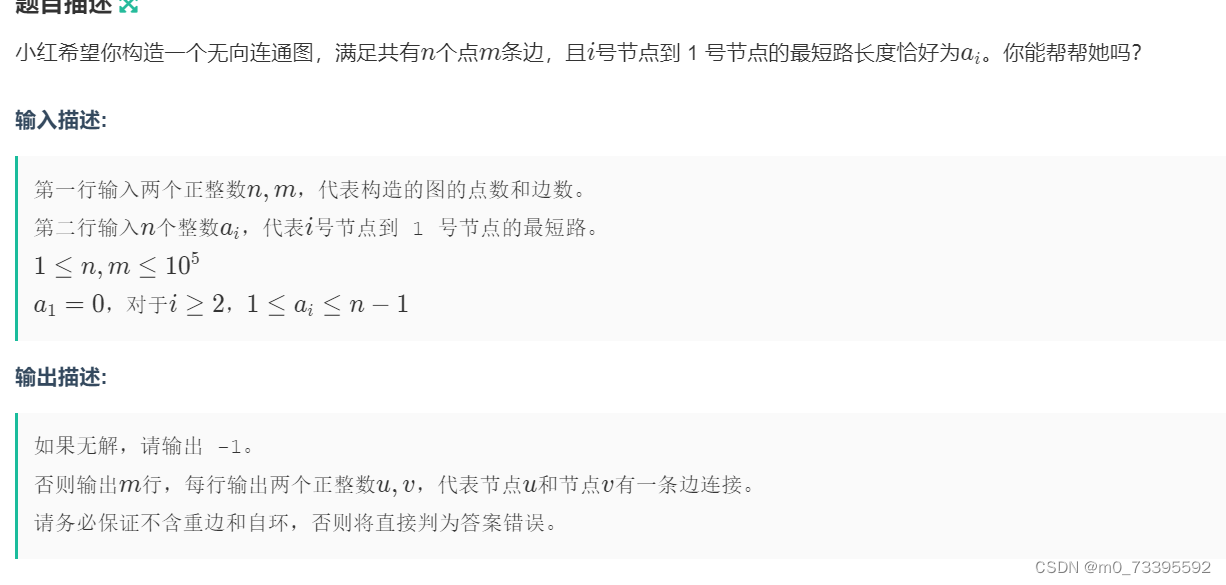
题意：

首先因为是最短我们肯定选择直接连，然后就可以发现他是一个分层图，每个点到1号点的最短路距离其实就是这个点所在的层数，当然我们排层次，我们要先去从小到大排序，这里我们拿vector<ll>e[n] 来存每个层数的点，我们第一想到的-1情况肯定是如果前一个层次没有点，我们无法构造这个层次的点。然后我们开始构造，从层次1开始，这里我们下层连上层的适合我们下层次就只要连上层次的第一个点，这样比较清晰哪个已经连过了，方便后添加边的处理，就这样连起来，然后最后如果m（能添加的边的数量）如果小于当前加边的数量，那肯定-1，如果直接等于当前连边的数量，那非常好，直接输出我们连的边就好。如果当前加的边小于m的话我们得考虑如何加边不影响这些点到1号点的最短路了。1.同层次的点互相连2.层次数差1的可以连起来（作者赛时也没想到）。在每加一条边的适合都判断加的边是不是已经等于m了，然后直接输出，如果所有能加的边全部都加上还小于m，那么也是-1的情况。

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define PII pair<ll,ll>
const int N=1e5+20;
vector<ll>e[N];
ll a[N];
ll n,m;
int main()
{
    cin >> n >> m;
    for(int i = 1 ;i <= n ; i++)
    {
        cin >> a[i];
        e[a[i]].push_back(i);
    }
    ll maxn = *max_element(a+1,a+1+n); //求最大距离
    for(int i = 1 ; i <= maxn ; i++)
    {
          if(e[i].size() == 0)
          {
              cout<<-1;
              return 0;
          }
    }
    vector<PII>ans;
    for(int i = 1 ;i <= maxn ; i++)
    {
        int u = e[i-1][0];
        for(auto it : e[i])
        {
            ans.push_back({u,it});
        }
    }
    if(ans.size() > m)
    {
        cout<<-1;
        return 0;
    }
    m-=ans.size();
    if(m > 0)
    {
        for(int i = 1 ; i <= maxn ; i++)
        {
            for(int j = 0 ;j < e[i].size() ; j++)
            {
                int u = e[i][j];
                for(int k = j+1 ; k < e[i].size() ; k++)
                {
                    int v = e[i][k];
                    ans.push_back({u,v});
                    m--;
                    if(m==0)
                        break;
                }
                if(m == 0)
                    break;
            }
            if(m == 0)
                break;
        }
    }
    if(m > 0)
    {
        for(int i = 2; i <= maxn ; i++)
        {
            if(e[i-1] .size() - 1 == 0)
            {
                continue;
            }
            for(int j = 1 ;j < e[i-1].size() ; j++)
            {
                for(auto it:e[i])
                {
                    ans.push_back({e[i-1][j],it});
                    m--;
                    if(m==0)
                        break;
                }
                if(m == 0)
                    break;
            }
            if(m == 0)
                break;
        }
    }
    if( m > 0)
    {
        cout<<-1;
    }
    else
    {
        for(auto it :ans)
        {
            cout<<it.first<<" "<<it.second<<"\n";
        }
    }
    return 0;
}

F/G

F	小红的子序列权值和（easy）

G	小红的子序列权值和（hard）

题意：

由于只有n的范围的区别，我们直接讲hard版本，首先我们必须了解一下乘法原理如果一个数n=p1^q1*p2^q2 * p3 ^q3，那么n的因数个数则有(q1+1)*(q2+1)*(q3+1)。本题是非空子序列之和，我们不需要考虑顺序问题，由于1不影响乘法最终的结果，我们只需要考虑有多少个2和又多少个3，这里我们用双重循环去遍历所有的情况，这里选取的时候则用到了组合数的原理，例举一种情况：2取2个，3取2个，1有5个（1的数量虽然不影响但他有2^cnt[1]种选法）这种情况对答案的贡献就是 (2+1)*(2+1)%mod*2^5%mod*C[cnt[2]][2]%mod*C[cnt[3]][2]%mod（C[i][j]为组合数，cnt[i]为i在数组中出现的次数），在求组合数的时候需要用到逆元，否则无法求1e5的数据，最后这个双重循环可以优化一下，例如a1*b1+a1*b2+a2*b1+a2*b2，我们可以优化成 (a1+a2) * (b1+b2)。

代码：

#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define PII pair<ll,ll>
const int N=1e5+20;
const ll mod = 1e9+7;
vector<ll>e[N];
ll n,m;
ll fastmi(ll a, ll b)
{
    ll res = 1 ;
    while(b)
    {
        if(b&1)
        {
            res = res * a % mod;
        }
        b>>=1;
        a = a * a % mod ;
    }
    return res;
}
ll jc[100100];
ll inv (ll x)
{
    return fastmi(x,mod-2);
}
ll c(ll x, ll y)
{
    return jc[x] * inv(jc[x-y]) % mod * inv(jc[y]) %mod;
}
int main()
{
    cin >> n;
    map<ll,ll>cnt;
    ll x;
    for(int i = 1 ; i <= n ; i++)
    {
        cin >> x;
        cnt[x]++;
    }
  //  cout<<fastmi(2,4)<<"\n";
    ll ans = 0;
    ll tmp = 1;
    jc[0] = 1;
    jc[1] = 1;
    for(int i = 2 ; i <= n ; i++)
        jc[i] = (jc[i-1]*i)%mod;
    for(int i = 1 ; i <= cnt[1] ; i++)
        tmp=(tmp*2)%mod;
    ll c2 = 0;
    ll c3 = 0;
    for(int i = 0 ; i <=cnt[2] ; i++)
    {
        c2 += c(cnt[2],i)*(i+1)%mod;
        c2%=mod;
    }
    for(int i = 0 ; i <=cnt[3] ; i++)
    {
        c3 += c(cnt[3],i)*(i+1)%mod;
        c3%=mod;
    }
    ans = c2 * c3 % mod *tmp % mod- 1 ;
   cout << ans;
    return 0;
}

ps：线性求逆元还不会，等亿会儿就补。

重新启动2.0

关注

22
点赞
踩
18

收藏

觉得还不错? 一键收藏
1
评论
牛客周赛35

这样比较清晰哪个已经连过了，方便后添加边的处理，就这样连起来，然后最后如果m（能添加的边的数量）如果小于当前加边的数量，那肯定-1，如果直接等于当前连边的数量，那非常好，直接输出我们连的边就好。首先因为是最短我们肯定选择直接连，然后就可以发现他是一个分层图，每个点到1号点的最短路距离其实就是这个点所在的层数，当然我们排层次，我们要先去从小到大排序，这里我们拿vectore[n] 来存每个层数的点，我们第一想到的-1情况肯定是如果前一个层次没有点，我们无法构造这个层次的点。
复制链接

扫一扫