MUSIC空间谱估计算法的MATLAB仿真_matlab music算法-CSDN博客

本文链接：https://blog.csdn.net/m0_73480582/article/details/145852887

0 前言

本博客是作者在学习国防科技大学的《阵列信号处理》慕课中的学习感悟，希望能够帮助有需要的朋友

本篇简单介绍了MUSIC算法，并且给出了公式结论，重点对MUSIC算法进行了MATLAB仿真，并且比较了MUSIC算法与CBF估计器的方位估计性能

1 MUSIC算法

1.1 简介

MUSIC算法（Multiple Signal Classification ），即多重信号分类算法，其最初的提出目标是为了提出一种能够突破瑞利限的超高分辨角度估计算法

理想情况如图：

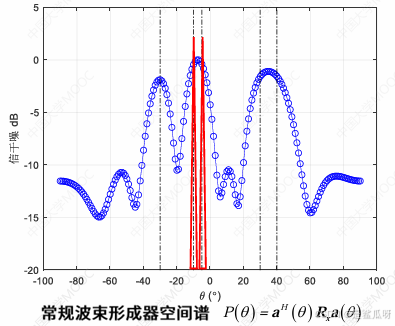
如果在信号来波方向能够获得一个波束宽度无限窄的尖峰，相当于其角分辨率无穷大，因此联想到要找到一个无穷小值

1.2 公式

先将协方差矩阵 $R_x$ 进行特征值分解，即将其分解为N个特征向量与特征值相乘之和的形式：

式中： $\theta_p$ 表示信号的来波方向，总共有 $P$ 个信号

实际上： $R_x$ 矩阵是一个 $N\times N$ 的矩阵，其进行特征值分解后会得到 $N$ 个特征值以及与其对应的 $N$ 个特征向量，这些特征值和特征向量实际上对应了接收信号中功率最高的前 $N$ 个信号，如果场中只有 $P$ 个声源在发声 $(P\leq N )$ ，那么这 $P$ 个声源就对应了前 $P$ 大的特征值，剩余的 $N-P$ 个特征值就与噪声对应

如果将信号对应的特征向量合并，就能得到信号子空间：

如果将噪声对应的特征向量合并，就能得到噪声子空间：

特征向量构成标准的正交向量组：

当 $a(\theta)$ 属于信号子空间， $v_n$ 属于噪声子空间，此时由于 $a(\theta)$ 与 $v_n$ 正交，因此导致其乘积为0

$\left|\boldsymbol{a}(\theta)^{H}\boldsymbol{v}_{n}\right|^{2}=0$

如果空间谱按照如下公式进行定义，此时空间谱会在信号源方向出现“谱峰”

基本思想：将阵列输出数据的协方差矩阵进行特征分解，得到与信号分量相对应的信号子空间和与信号分量正交的噪声子空间，利用这两个子空间的正交性来估计信号的参数。

MUSIC算法步骤（这里是本篇最重要的地方）：

由阵列接收数组 $x(t_k)$ 估计 $\hat{\boldsymbol{R}}_x=\frac{1}{K}\sum_{k=1}^K\boldsymbol{x}\left(t_k\right)\boldsymbol{x}^H\left(t_k\right)$
对特征值 $\hat{\boldsymbol{R}}_x$ 作特征分解，用 $N-P$ 个小特征值对应的特征矢量构成 $V_n$
用搜索矢量 $a(\theta)$ 向 $V_n$ 作投影计算谱峰：

注意：谱峰与信号强度无关，只反应 $a(\theta)$ 与 $V_n$ 的正交性

1.3 慕课MUSIC算法图片

慕课展示了一个10元均匀直线阵列下CBF估计器与MUSIC算法的估计性能比较，来波方向分别为60°，80°，85°，120°，130°，信噪比SNR均为5dB

2 MATLAB仿真

本程序进行了5个方向来波信号的仿真，其参数均与慕课相同，有需要读者可以自行更改

2.1 参数设置

阵元数目	10
信号方向	[60 80 85 120 130]°
信噪比	[5 5 5 5 5]dB

2.2 代码实现

%三清
clc;
clear;
close all;

% 参数设置
N = 10;     %均匀直线阵列阵元个数
lamda = 1;  %假设波长为1m
L = 1000;   %快拍个数
d = lamda/2;%阵元间距假设为半波长
fs = 1000;  %采样频率
f0 = [31;69;118;253;344];%来波信号频率，可以根据实际要求进行更改
t = [0:L-1]/fs; %时间序列

%来波方向角度，可以根据实际要求进行更改
theta_coming = [60 80 85 120 130]; 

% 计算来波个数
P = length(theta_coming);

%来波信号信噪比，可以根据实际要求进行更改
SNR = [5;5;5;5;5];

% 生成阵列响应向量
a = @(theta) exp(1i * 2 * pi * d * (0:N-1)' * cosd(theta) / lamda);

% 生成方向矢量
vs = a(theta_coming);%生成信号方向矢量

% 构建目标信号
s = exp(1i*2*pi*f0*t);

% 构建来波信号
xs = vs * (s .* sqrt(10.^(SNR/10)));

% 构建噪声信号
xn = sqrt(2) * (randn(N,L) + 1i * randn(N,L));

% 构建接收信号
x = xn + xs;

% 构建协方差矩阵
R_x = (x * x')/L;

% 对协方差矩阵进行特征值分解
% V是特征向量拼接成的特征向量组，D是特征值的对角阵
[V,D] = eig(R_x);

% 按照特征值的大小进行重新排序（虽然好像eig已经按照从小到大进行了排序）
% d是特征值，order是顺序
[d,order] = sort(diag(D));

% 按照从小到大排序重建对角阵
D_order = D(order,order);

% 按照从小到大排序重建特征向量组
V_order = V(:,order);

% 提取噪声子空间
Vn = V_order(:,1:N-P);

% 扫描角度设置，从0扫描到180度，这里细分为3600份，也可以分的更细致一点
theta = linspace(0,180,3600);

% 构建扫描方向向量
v = a(theta);

% 创建0初值的空间谱，长度应该与扫描角度数量相同
P_MUSIC = zeros(1,length(theta));

% 运用循环给空间谱进行一一赋值
for i = 1:length(P_MUSIC)
    P_MUSIC(i) = 1./ sum(abs((v(:,i)' * Vn)).^2,2);
end

% 这里取对数是为了方便观察
P_MUSIC = 10 * log10(P_MUSIC);

% 计算CBF空间功率谱
P_CBF = abs(sum(v' .* (R_x * v).',2));
P_CBF = 10 * log10(P_CBF);

% 对两种方位估计算法进行归一化，使得能够比较其角分辨率
P_MUSIC = P_MUSIC - max(P_MUSIC);
P_CBF = P_CBF - max(P_CBF);


% 后处理绘图
figure;
hold on;
plot(theta,P_CBF,"LineWidth",1,"Color",[38, 188, 213]/255);%绘制曲线，设置粗细
plot(theta,P_MUSIC,"LineWidth",1,"Color",[255, 150, 128]/255);%绘制曲线，设置粗细
grid on;%绘制网格
xlim([0 180]);%限制x轴范围从0到180度
ylim([min(P_MUSIC)-5 5]);%限制y轴范围
xlabel("角度/°");%绘制x轴标签
ylabel("归一化幅度/dB");%绘制y轴标签
title(sprintf("%d元均匀线阵空间指向性", N),'FontWeight', 'bold',"FontSize",12);%绘制标题，加粗，设置大小
set(gca,"LineWidth",1);%设置坐标轴粗细
set(gca,"FontSize",12);%设置坐标轴字体大小
set(gca, 'FontWeight', 'bold');%加粗坐标轴文本

% 在来波方向角度添加直线，方便观察
for k = 1:length(theta_coming)
    xline(theta_coming(k), '-', '来波方向',"Color",[95, 92, 51]/255,"LineWidth",1,"FontSize",8,'FontWeight', 'bold','LabelVerticalAlignment','bottom');
end
% 绘制图例
legend("CBF",'MUSIC','','','','','');